针对分布式存储中多节点再生修复的修复带宽和可靠性问题,提出了一种具有健康节点协作的多节点修复方案. 该方案在修复模型上做出了相应改进,通过健康节点间的协作把上述问题做了折中. 给出了具体的多节点修复过程和相应再生码的构造,用信息流图求得最大流最小割集来说明其最小边界. 结果表明,在确保修复带宽最低的条件下使修复时间同步,修复过程更简便,最重要的是所需传输信道更少,保证了修复的可靠性.
In distributed storage systems, an efficient multi-node regenerating program with healthy nodes collaboration was proposed to make a trand-off between the repair bandwidth and reliability for multi-node regeneration. Specific multi-node repair process and the construction of regenerating code were introduced, and the max-flow-min-cut of information flow graph was used to illustrate its lower bound. It is shown that the program ensures the repair bandwidth maintain to minimum during the repair process, and makes the repair time synchronization and repair process easier. The most important is less that of desired transmission channels when ensuring reliability of regeneration.
分布式存储是云存储中最主要的存储方式[1],在分布式存储系统中,由于节点自身因素或外界的破坏,时常会发生节点损坏的情况,为了提高可用性和可靠性,需要对损坏的节点进行修复(再生). 针对多节点再生问题,文献[2]给出了联合再生节点方案,需要更多的传输信道,这使得修复过程更加繁琐,导致修复的不稳定. 另外,Kathrin等[5]指出,再生码的运用对于限制所占用网络带宽和存储容量是很好的选择,但还需要更高的可靠性. 因此,保证修复的高成功率是非常重要的,在考虑传送数据尽量少的同时,也需要尽量减少传送次数,同时减少了线路成本.
针对这些问题,笔者提出了一种具有健康节点协作的多节点修复方案,并与现有的方案进行了比较分析.
1 多节点再生修复模型为了表达方便,符号说明如下.
B:源文件的大小;
k:系统节点个数;
n:系统节点和冗余节点的总数目;
d:修复一个受损节点所需的健康节点数;
r:失效节点数目;
α:分布式存储每个存储节点数据的存储大小(B/k);
β:修复受损节点的修复带宽;
γ:修复失效节点所需带宽.
传统的多节点再生就是新节点(中间节点,newcomer)选择任意k个健康节点(包括系统节点与冗余节点)还原出源文件,这样可以得出任何失效的节点数据,下面以文献[6]中节点的编码方式为例介绍传统的多节点再生修复模型,如图 1所示. 源文件A1、A2、B1、B2被均匀地分布在k(k=2)个系统节点中,并用源文件构造出了n-k=2 (n=4)个冗余节点,假设第2个系统节点和第4个冗余节点失效,中间节点选择了剩下的k(k=2)个健康节点下载数据,恢复出源文件(A1、A2、B1、B2),从而修复失效的这2个节点.
|
图 1 传统的多节点再生修复模型 |
为了实现精确修复,每个失效节点都需要恢复出整个源文件,从修复带宽来看,花费了γ=k(B/k)=B大小的带宽来达到修复出B/k大小数据的目的. 虽然修复过程简便,却需付出很大的代价,得到了很多不必要的数据,当面对大数据时,绝大部分的数据都是无用的数据,此方案的不足就更加明显了,在实际操作中并不适用.
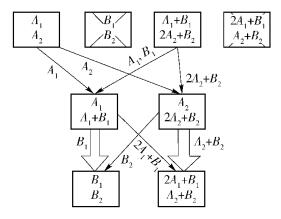
针对减小修复带宽的问题,Shum[4]提出了多节点联合修复方案,如图 2所示,同样假设第2个与第4个节点损坏的情况,运用以下2个过程来修复受损节点.
|
图 2 多节点联合修复方案[4] |
第1个过程:第1个节点和第3个节点分别传输A1和A1+B12个数据块到一个新节点,并且分别传输A2和2A2+B2到另一个新节点,形成了2个新节点,数据带宽分别为dβ1 (d=2).
第2个过程:这2个新节点再互相传输数据块B2和2A1+B1给对方,再通过计算形成修复出的第2个节点和第4个节点,数据带宽分别为
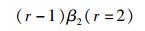
|
可以得出每个失效节点所需的修复带宽为

|
与传统修复方案相比,多节点联合修复方案明显减少了传输数据的大小,降低了修复带宽,但是增加了一个修复过程,并且增加了传输过程的传输次数. 在修复过程中数据传输方面错综复杂,除了健康节点需要传输数据到新节点外,新节点之间还需要相互传输数据,当传输距离非常远时,很有可能出现数据传输异常,修复失败的几率大大增加,同时更多的传输线路增加了修复负担,需要耗费更大的资源,不能较好地运用于实际操作中. 针对这个问题,笔者提出了一种高效的具有健康节点协作的多节点修复方案,不仅使修复过程更简便,减少了修复负担,还同时考虑了修复带宽问题,对实际的运用更加适用.
2 健康节点协作的多节点修复过程根据上述分析,可以使这d个用来修复失效节点的健康节点互相协作,省掉中间节点这个过程,从中任意选择一个健康节点来代替新节点,将这个节点用m表示,直接在m上对受损节点进行修复.
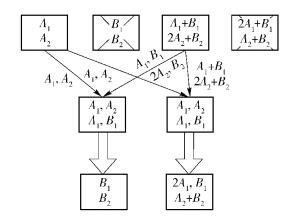
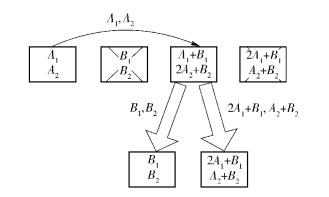
具有健康节点协作的多节点修复过程如图 3所示. 同样假设第2个与第4个节点损坏的情况下,选择第3个节点为m,第1个节点直接将其存储的A1和A22个数据块传输给m,然后再在m上与其自身的数据进行运算,可以同时得出2个受损节点的数据并分别输出,从而修复出受损节点.
|
图 3 具有健康节点协作的多节点修复过程 |
假设r个节点失效后,需要d个节点来修复,系统管理员从健康节点中选择1个节点作为m,其他健康节点传送数据到接收端m,则需要传送d-1次大小为β的数据,再通过线性运算并输出r个大小为α的数据,因此,修复出所有的失效节点所需修复带宽为γ=(d-1)β+rα.
该方案与联合修复方案相比,两者传输数据量大小相同(6个数据块),但该方案有效地减少了传输次数(传输线路),联合修复方案需要6次,而该方案只需要3次,并且修复过程也从2个化简为1个,达到了同样的修复目的.
在云存储环境中,当每个节点相隔距离非常大时,整个修复过程更加安全、简便. 进一步,如果修复出的节点与第3个节点相隔非常近,甚至在同一个服务器上,那么这种方案的优势就更加突出了,只需要传输1次数据并且修复带宽只有2个数据块的大小,便可以快速简便地达到修复目的了.
3 信息流图及最小割集证明在节点再生过程中,通过求值信息流图的最大流和最小割集,得到所需修复带宽最小值. 对于1个大小为B的源文件被编码后分散在n个存储节点中,其中源文件(S)被等分存储在k(k﹤n)个存储节点中,另外的n-k个节点为冗余节点. 根据MDS(maximum distance separable)码特性[7],任意k个节点(包括系统节点和冗余节点)就可以恢复出源文件,当数据收集器(DC, data collectors)需要整个文件时,只需从n个节点中下载k个节点即可恢复出源文件.
设源文件(S)到所有被等分存储数据的存储节点的阶段过程为stage-1,传输的数据为无穷大;同时每个存储节点被等分的数据大小为α,设存储节点内部存储数据的流向为stage 0,传输的数据大小为α;把stage 0以后的每个stage定为1个修复过程,设失效节点的第1个修复过程为stage 1,剩下的健康节点传输大小为β的数据,然后将得到的数据和自身存储的数据进行相应的运算,得到受损节点所存储的数据并输出,且输出数据大小为存储节点的存储量α;依次类推,把修复过程区分为不同的阶段,表示为v(v-1,v0,v1,…,vh),每个阶段所修复出的节点的集合依次为Sv1,Sv2,Sv3,…,Svh,i=1,2,…,h,i为其相应的阶段. DC连接的总的节点数为k,设这k个节点的集合为R,并且满足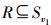
|
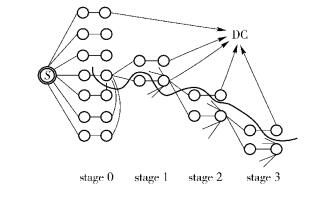
图 4 信息流图及一个割集实例 |
对信息流图切割时就是把从源节点到DC的这条信息流上所有的顶点V分为2部分,一部分在源节点这边,另一部分在DC这边,在割线上的信息量的总和就是割集,最小割集是在保证降低修复带宽的同时,使得信息流的总和不小于源文件的大小B. 以每个阶段为单元,可以把每个阶段的切割分为2种,一种是切割α和β,另一种则只是切割α,根据这2种切割可以画出图 4所示的割线. 设每个阶段中被割线分开在DC这边的再生节点数为li,且满足条件l1+l2+l3+…+lh=k, li≤r,h≤k.
以每个stage为单位,选择这2种切割中的信息量较小的一种,然后把每个stage的信息流容量相加得出总和,这个总和不小于源文件大小B,根据这样的信息流图可以得出最小流的总和公式为
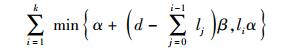
|
(1) |
所切割的信息流量应尽量小,只要其总和不小于源文件的大小即可,即
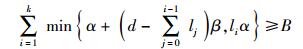
|
(2) |
为便于对比,利用与文献[4]中相同的参数:n=4,d=k=r=2,B=4,α=B/k=2. 为了求得最小的β值,把参数(l1,l2)的2组参数值(1,1)和(2,0)[4]代入式(2),分别为

|
综合得到β≥2. 根据第2节结果,修复2个失效节点所需的修复带宽γ=(d-1)β+rα,将上述参数值代入得6,平均每个失效节点所需的修复带宽为3,与联合修复方案的修复带宽相同. 若是在同一个服务器上,省去输出修复好的节点所需带宽的话,就只需 (d-1)β=2大小的总的带宽,平均每个节点为1. 因此,该方案具有明显的优势,在修复失效节点时下载数据是同步的,且修复步骤简便、安全易实施,有效地减少了所需的数据传输信道,保证了高效率地修复节点,减少了对资源的浪费.
4 健康节点协作多节点修复再生码的构造下面给出再生码的一种构造方法. 关于具有健康节点协作的多节点修复方案中,将源文件B等分为许多个块并分布在k个存储节点上,并把每个节点的数据分成k份,称为系统节点,这些节点形成一个k×k阶矩阵G1,在矩阵G1中每一列miT(i=1,2,…,k)表示了每个节点的数据信息. 在GF(q)上所有系统节点可以表示为
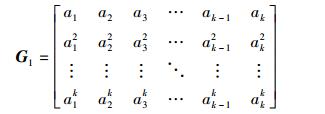
|
为了增大系统的可靠性,把源文件的数据用同样的网络编码产生n-k个冗余节点,这些冗余节点的数据结构用k×n阶矩阵G2表示,每一列miT(i=k+1,…,n)表示了每个冗余节点的数据信息. 矩阵G2为

|
矩阵G1和G2中所有的存储节点组成了完整的分布式存储系统. 当一些节点受损,用d个节点来修复这些节点时,每个节点需要下载的数据大小为β,需要传输到m的节点数据miT的总数为d-1,形成k×(d-1)阶矩阵,把所有用来修复节点的数据集中在m上,用来修复失效节点的数据为k×d阶矩阵,设为C. 通过线性运算得到受损节点相应的再生节点后,把每个节点的修复数据γ与节点数据大小的线性关系用α×γ阶矩阵M(i)(2≤i≤n-k)表示,通过线性运算最终得出每个大小为α的再生节点,这些再生节点数据用矩阵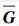
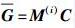
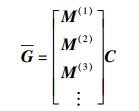
|
由于从健康节点下载的数据 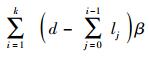
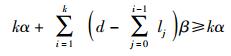
|
(3) |
因此

|
(4) |
即有
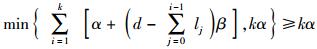
|
(5) |
这样
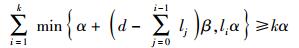
|
(6) |
设k=B/α,得出
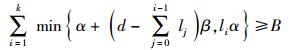
|
(7) |
因此式(2)是成立的. 从而,再生码的构造符合要求,信息流总和不小于源文件B,在减小修复带宽的条件下可以修复出受损节点.
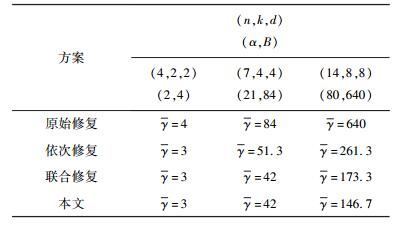
5 现有多节点修复方案的比较将几种典型的多节点修复方案(原始修复方案[8]、依次修复方案[6]、联合修复方案[4])与本文方案进行对比. 当k=d, r=n-k,且n﹤2k时,把相关参数用集合的形式表示为(n, k, d)(α, B).
用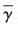
|
|
表 1 多节点修复方案平均每个节点修复带宽比较 |
在修复过程中,在网络资源里传输数据所用传输信道数f越小也使系统越可靠,操作简单易行. 各方案所用的传输信道数如表 2所示. 可以明显地看出,本文方案在保证达到目前所有方案最低修复带宽的条件下,有效地减少了修复传输信道数,简化了修复过程,增加了可靠性,减少了对网络资源的浪费,达到了安全高效地修复节点的目的.
|
|
表 2 修复过程中传输数据所用传输信道数比较 |
在分布式存储越来越广泛运用的当今,保证节点高效安全地存储数据是至关重要的. 针对分布式存储中多节点再生修复的修复带宽和可靠性问题,提出了一种高效的具有健康节点协作的多节点修复方案. 该方案在修复模型上做出了相应改进,通过健康节点间的协作把上述问题做了一个很好的折中. 在确保修复带宽最低的条件下,使修复时间同步,修复过程更简便,最重要的是所需传输信道更少,保证了修复的安全可靠性.
| [1] | Dimakis A G, Ramchandran K, Wu Y, et al. A survey on network codes for distributed storage[J]. Proceedings of the IEEE, 2011, 99(3): 476–489. doi: 10.1109/JPROC.2010.2096170 |
| [2] | Hu Y, Xu Y, Wang X, et al. Cooperative recovery of distributed storage systems from multiple losses with network coding[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 268–275. doi: 10.1109/JSAC.2010.100216 |
| [3] | Shum K W, Hu Y. Exact minimum-repair-bandwidth cooperative regenerating codes for distributed storage systems[C]//IEEE International Symposium on Information Theory Proceedings (ISIT). Saint-Petersburg, Russia: IEEE Press, 2011: 1442-1446. http://www.oalib.com/paper/4161797 |
| [4] | Shum K W. Cooperative regenerating codes for distributed storage systems[C]//IEEE International Conference on Communications (ICC). Tokyo, Japan: IEEE Press, 2011: 1-5. http://www.oalib.com/paper/4161797 |
| [5] | Kathrin Peter, Sobe Peter. Application of regenerating codes for fault tolerance in distributed storage systems[C]//IEEE 11th International Symposium on Network Computing and Applications. Cambridge, MA, USA: IEEE Press, 2012: 67-70. http://ieeexplore.ieee.org/xpl/mostRecentIssue.jsp?punumber=6298766 |
| [6] | Wu Y, Dimakis A G. Reducing repair trafflc for erasure coding-based storage via interference alignment[C]//IEEE International Symposium on Information Theory (ISIT). Seoul: IEEE Press, 2009: 2276-2280. http://www.oalib.com/paper/4161797 |
| [7] | Mac-williams F J, Sloane N J A. The theory of error-correcting codes[M]. North-Holland, New York: Elsevier, 1977: 762. |
| [8] | Dimakis A G, Godfrey P B, Wainwright M J, et al. Network coding for distributed storage systems[C]//IEEE International Conference on Computer (INFOCOM). Anchorage, Alaska: IEEE Press, 2007: 2000-2008. http://www.oalib.com/paper/4161797 |