为实现低复杂度条件下的长码软扩频,提出了一种基于准规则低密度奇偶校验码(QR-LDPC)的软扩频方法. 利用编码度优化的方法构造了一种QR-LDPC. 提出了一种基于编码约束的同步方法,降低了长码软扩频系统的同步复杂度. 仿真结果表明,基于QR-LDPC的软扩频方法是一种有效、可行的长码软扩频方法,可同时获得较大的扩频增益和编码增益;相同扩频比条件下,系统误码率性能优于传统的直接序列扩频系统.
In order to realize a low complexity tamed spread spectrum system based on long codes, a novel tamed spread spectrum system based on quasi-regular low density parity check (QR-LDPC) code was proposed. This system employs a new LDPC code called quasi-regular LDPC which is constructed using degree distribution optimization method. A synchronization algorithm exploits check constraint was proposed, and then the complexity of synchronization for long code tamed spread spectrum was reduced. Simulations show that the proposed tamed spread spectrum is an effective and feasible scheme adopt long codes, both spreading gain and coding gain could be achieved. The bit error rate performance of proposed system is also better than traditional direct sequence spread spectrum system since the spread factor is equal.
软扩频是直接序列扩频技术与编码技术相结合而发展起来的一种新型基带扩频技术,它有效改善了传统扩频技术频谱效率低的缺点. 美军的联合战术信息分配系统(JTIDS,joint tactical information distribution system)采用了32位M序列的(32, 5)软扩频技术,IEEE 802.11采用了多相补码键控(CCK, complementary code keying)软扩频技术. 受正交扩频码组和接收端相关器数目的影响,现有软扩频技术的研究[1-2]主要局限于短码软扩频,系统扩频增益和编码增益严重受限.
笔者提出了一种LDPC编码软扩频(LDPC-TSS,low density parity code-tamed spread spectrum)方法,可实现低复杂度条件下的长码软扩频. 提出了LDPC-TSS的系统模型和接收机方案,结合方案提出了QR-LDPC构造方法;同时提出了基于编码约束的软扩频同步算法,克服了传统软扩频系统中相关器数目对扩频码码长的限制. 通过仿真实验,对LDPC-TSS与传统直接序列扩频(DSSS,direct sequence spread spectrum)在加性高斯白噪声(AWGN,additive white Gaussian noise)信道条件下的误码率(BER,bit error rate)性能进行了分析比较. 仿真结果表明,LDPC-TSS可同时获得扩频增益和编码增益,BER性能明显优于传统直接序列扩频系统.
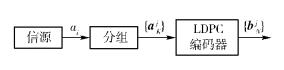
1 LDPC编码软扩频系统模型LDPC-TSS系统模型如图 1所示.
|
图 1 LDPC-TSS系统模型 |
LDPC编码软扩频首先需要对信息序列{ai,0≤i≤∞}进行分组,每K bit为一组,aKj=(ajK,ajK+1,…,a(j+1)K-1)表示第j个长度为K的信息序列分组. 采用LDPC编码的软扩频模型可表示为
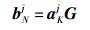
|
(1) |
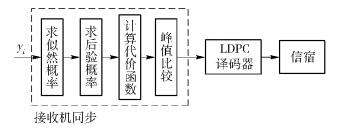
其中:G为生成矩阵,bNj=(bjN,bjN+1,…,b(j+1)N-1)为第j个长度为N的扩频序列. LDPC编码软扩频的扩频比f=1/R,R=K/N为LDPC编码的码率. 接收机框图如图 2所示.
|
图 2 LDPC-TSS接收机框图 |
软扩频接收机主要由同步和译码2部分组成. 同步可采用串行搜索的方式,找到一组接收符号满足编码约束的概率最大,实现同步. 该同步方法基于LDPC校验矩阵的稀疏特性设计,同步复杂度较低. 同步完成后,可按同步结果分组送入LDPC译码器,经译码输出至信宿,完成接收.
2 编码度优化的QR-LDPC构造LDPC码集可由一对度分布参数(r,c)确定[3]. 行编码度为r={rd,1≤d≤tr},其中rd为行重d在校验矩阵中所占的比例,tr为校验矩阵的最大行重;列编码度为c={cd,1≤d≤tc},其中cd为列重d在校验矩阵中所占的比例,tc为校验矩阵的最大列重. 采用密度进化理论、高斯近似方法对编码度分布(r,c)进行优化,可以构造高性能的LDPC码[4-5].
定义QR-LDPC码的行编码度分布满足
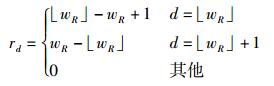
|
(2) |
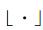
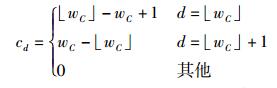
|
(3) |
通过扫描不同编码度的典型码集合,可找出达到目标BER所需的信噪比(门限信噪比),由于BER是信噪比的单调函数,因此门限信噪比可通过二分法快速搜索得到,具体实现步骤如下.
步骤1 初始化,设定目标BER为Bd,误差范围为ε,编码度wR搜索范围为[wRmin,wRmax].
步骤2 门限信噪比测试.
1) 根据编码度参数wR构造LDPC码字[3],并初始化信噪比S=S0、信噪比修正参数Δ.
2) 依据1)中构造的LDPC码,通过计算机仿真得到对应信噪比条件下的BER为Bs.
3) 如果|Bs-Bd|≤ε·Bd,则当前信噪比为编码度wR对应的门限信噪比,转向1),对下一个编码度参数进行测试;否则,步骤4).
4) 如果Bs-Bd>0,则设置信噪比S=S+Δ、Δ=Δ/2,并转向2)继续;如果Bs-Bd﹤0,则设置信噪比S=S-Δ、Δ=Δ/2,并转向2)继续.
通过门限信噪比测试,可得到编码度搜索区间[wRmin,wRmax]内,编码度参数wR对应的门限信噪比.
步骤3 比较不同编码度参数对应的门限信噪比,则最小门限信噪比对应的编码度参数wR即为最优的编码度参数.
设定目标BER Bd=10-3、误差范围ε=0.01、编码度wR搜索区间[2,8].
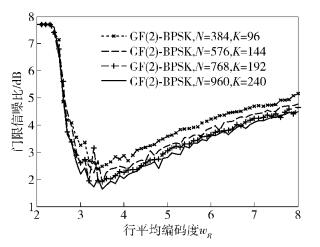
图 3是扩频比为4时,不同码长条件下,平均行编码度与门限信噪比之间的关系. 仿真结果显示,平均行编码度为3.5时可达到稳定的最佳性能;同时,码长越大,对应的门限信噪比越小.
|
图 3 扩频比为4时,准规则LDPC码对应行编码度与门限信噪比的关 |
LDPC-TSS系统可利用校验矩阵进行同步[6-7],通过计算接收符号满足校验方程组的概率,找到接收符号满足校验方程组概率最大的位置,实现同步.
LDPC-TSS系统中,发送端的编码输出bi(-∞﹤i﹤+∞)经二进制相移键控(BPSK,binary phase shift keying)调制和信道传输后,接收端信号可表示为yi=(1-2bi)+ni,其中ni表示均值为0、方差为σ2的加性高斯白噪声,可得到似然概率:
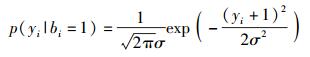
|
(4) |
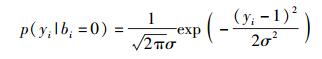
|
(5) |
定义代价函数为
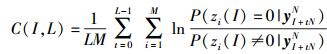
|
(6) |
其中:ylN=(yl,yl+1,…,yl+N-1)表示以时刻l为起始时间、长度为N的一组接收符号;zi(·)=0表示“第i个校验方程可以满足”,否则zi(I)≠0;M为用于同步的校验方程个数;L为用于同步的码组个数.
如果偏移量I对齐码组,则每一个校验方程都应该以较高的概率满足,其结果是代价函数C(I,L)的值最大;当偏移量I没有对齐码组时,校验方程组满足的概率低,代价函数C(I,L)的值将很小. 利用这一特性,同步输出为
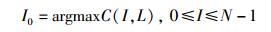
|
(7) |
基于编码约束的同步算法实现步骤如下.
步骤1 根据式(4)、式(5)计算后验概率:
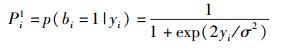
|
(8) |
步骤2 从任意时刻开始,连续选取(L+1)N个接收符号;以偏移量i(0﹤I﹤N-1)对应的数据为起点,取L组,每组N个符号;分别对各个校验方程,根据步骤1的结果计算各数据组的后验概率值,得到满足第i个校验方程zi的后验概率:
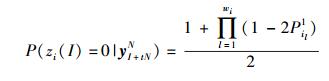
|
(9) |
其中:wi为H矩阵第i行的行重,il为H矩阵第i行第l个1对应的列标. 同理可得
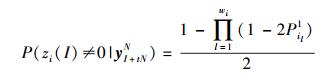
|
(10) |
步骤3 在偏移量为I的情况下,将式(9)、式(10)代入式(6),计算代价函数C(I,L):
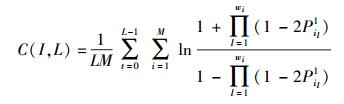
|
(11) |
对应N个偏移量,可计算得到N个C(I,L)值.
步骤4 依据代价函数的大小进行峰值判决,取C(I,L)最大值对应的偏移量Imax为码字对齐位置,即为同步输出结果.
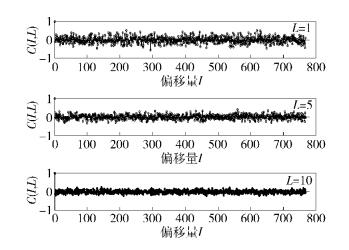
采用所提出的准规则LDPC码验证该同步方法,假设扩频比为4,码长N=384,分别计算信噪比为-3 dB时,L=1、L=5和L=10这3种情况下的代价函数C(I,L). 同步仿真结果如图 4所示,横坐标表示偏移量I,纵坐标为归一化的同步代价函数C(I,L). 可以看出,随着码组数L的增加,同步性能越来越好. 仿真表明,基于编码约束的同步算法可在较低信噪比条件下准确地实现同步. 同步过程中,参数L的选取,需综合考虑码率、码长及信噪比等参数,通过仿真等方式最终确定.
|
图 4 基于编码约束的同步结果 |
假设同步过程中,仅采用一个码组的接收符号进行同步. 传统的软扩频同步由2K个序列长度为N的相关器和一个2K选1的比较器组成. 完成1个码相位的搜索共需进行N×2K次乘法和(N-1)×2K次加法;相关器计算结果的比较输出需要2K-1次比较运算.
采用基于编码约束的同步算法,当L=1时,完成1个偏移量I计算的代价函数为
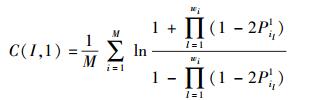
|
完成一次计算,需要进行M(wR+2)+1次加法运算、2MwR次乘法运算、M+1次除法运算、M次对数运算和N-1次比较运算.
因此,要采用L个数据分组完成N个偏移量的同步计算,算法复杂度约为前述计算量的LM倍. 通过比较可以看出,在长码软扩频系统中,传统同步方法的计算复杂度为指数量级,不具可行性;基于编码约束的同步算法,可将计算复杂度降低为多项式量级,是一种可行的同步方法.
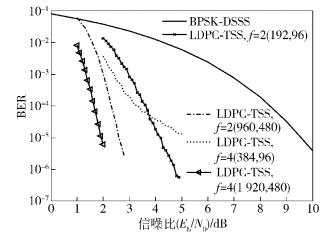
4 仿真分析为验证LDPC-TSS通信系统的性能,将其与传统DSSS通信系统性能进行了比较仿真实验. 仿真中采用AWGN信道,调制方式为BPSK调制. LDPC译码采用对数域置信传播(Log-BP,logarithm belief propagation)译码算法,最大迭代次数为100. 图 5是扩频比为2、4时,LDPC-TSS系统与BPSK-DSSS通信系统的性能仿真比较. 仿真结果表明,在相同扩频比条件下,LDPC-TSS的性能要明显优于BPSK-DSSS,而且LDPC码长越大,LDPC-TSS的性能越优.
|
图 5 LDPC-TSS 系统性能仿真 |
基于准规则LDPC码的软扩频方法,提出了一种LDPC编码软扩频系统模型和接收机方案. 结合系统方案,提出了准规则LDPC码字构造方法和一种基于编码约束的同步算法. 通过计算机,对软扩频系统在AWGN信道条件下进行了BER性能仿真. 仿真结果表明,采用LDPC-TSS系统较BPSK-DSSS有着明显的性能优势,并且LDPC-TSS可同时获得扩频增益和编码增益,LDPC-TSS是一种有效、可行的长码软扩频方法.
| [1] | Pursley M B, Royster T C. High-rate direct-sequence spread spectrum with error-control coding[J]. IEEE Transactions on Communications, 2006, 54(9): 1693–1702. doi: 10.1109/TCOMM.2006.881256 |
| [2] | Zhao Zixin, Guo Shuxiang. An FHMA acoustic communication system for multiple underwater robots[C]//Proceedings of the 2010 IEEE International Conference on Information and Automation (ICIA). Harbin: [s.n.], 2010: 1223-1228. |
| [3] | Davey M C. Error-correction using low-density parity-check codes[D]. PhD Thesis: University of Cambridge, 1999. |
| [4] | Richardson T, Shokrollahi A, Urabanke R. Design of capacity-approaching irregular low-density parity-check codes[J]. IEEE Transactions on Information Theory, 2001, 47(2): 619–637. doi: 10.1109/18.910578 |
| [5] |
李二保, 雷菁, 徐富兵. 非规则LDPC度分布优化设计[J]. 电子与信息学报, 2008, 30(11): 2788–2791.
Li Erbao, Lei Jing, Xu Fubing. Design and optimization of degree distributions of irregular LDPC[J]. Journal of Electronics and Information Technology, 2008, 30(11): 2788–2791. |
| [6] | Rodrigue Imad, Sebastien Houche. Theoretical analysis of a MAP based blind frame synchronizer[J]. IEEE Transactions on Wireless Communications, 2009, 8(11): 5472–5476. doi: 10.1109/TWC.2009.090410 |
| [7] | Qi Yinghao, Liu Tao, Rong Mengtian. Reduced complexity algorithm for QC-LDPC coded blind frame synchronization[J]. IEICE Transactions on Communications, 2011, 94(4): 1057–1061. |


