针对经典DV-hop算法在估计跳数时所引起的定位误差,提出了基于覆盖比例的定位算法. 根据两节点间的通信覆盖率引入跳数系数,降低了每跳距离产生的误差,精确未知节点距参考节点的位置. 仿真结果表明,改进的算法能使节点的定位精确度提高,使误差比原始算法降低10%左右.
In wireless sensor networks, the localization of nodes is vital and promising to a wide scope of applications. Based on characteristics of DV-hop, an improved algorithm for the typical range-free localization was proposed. The main principle of the improved algorithm is to introduce hop coefficient to revision hops, which could address the problem that DV-hop localization of wireless sensor networks produces error of hops stimulation. Then hop coefficient could bring down the error of per hop average distances and be sure precisely unknown nodes and reference node. Simulation demonstrates that the results of improved algorithm are more accurate, and the errors down to about 10%.
无线传感器网络由部署在监测区域内大量的微型传感器节点组成,通过无线通信方式形成一个多跳的自组织的网络系统. 其目的是协作地感知、采集和处理网络覆盖区域中被感知对象的信息,并发送给观察者[1]. 传感器、感知对象和观察者构成了无线传感器网络的3个要素. 无线传感器网络能获取客观物理信息,具有非常广阔的应用前景.
而在大多数应用中,无线传感器的定位又显得尤为重要. 因为只有确定了方位,收集到的数据才有其具体的意义. 研究者们不断地提出新的无线传感器的定位算法,其大致分为3类:主动模式,基于距离的定位,目前常选择利用接收的信号强度指示[2]进行跟踪定位;被动模式,与距离无关的定位,对节点到目标间的距离进行估计,然后通过三边测量法或极大似然估计法进行定位[3];基于声波衰减的定位,根据经验测量获得比较接近实际的模型,然后进行定位.
3类方法各有其优势与不足. 第1类方法的实现需要购置附加的硬件设备,测距效果受到环境影响比较大;第3类方法定位误差比较大;而第2类方法成本低廉,受环境影响小,因而得到更多的重视. Dragos Niculescu及Badri Nath提出的DV-hop算法[2,4]是目前应用较为广泛的基于连通性的定位算法,但DV-hop算法在计算未知节点到锚节点距离时具有较大的误差. 根据经典的DV-hop算法,引入跳数系数,提出了一种改进DV-hop算法,减小定位误差.
1 1DV-hop算法 1.1 DV-hop算法思想1) 将锚节点向量分组初始化,跳数为零. 每个锚节点向其邻居节点广播自身跳数及坐标方位,接收节点记录下每个锚节点最小跳数的向量分组,忽略来自同一锚节点较大跳数的向量分组,然后将跳数加1再转发给邻居节点,如此往复转发以后,网络中每个节点都可得到到达各个锚节点的最小跳数信息[5].
2) 每个锚节点根据第1)步中记录的其他锚节点的位置和跳数信息,利用式(1)估算平均每跳距离.

|
(1) |
其中:(xi,yi)、(xj,yj)分别为锚节点i和j的坐标,hj为锚节点i与j(j不等于i)之间的跳数.
3) 锚节点将计算得到的平均每跳距离广播到网络中, 未知节点查找距离自身跳数最小的那个锚节点发来的平均每跳距离,并转发给邻居节点,舍弃其他锚节点的平均每跳距离.
4) 未知节点根据接收到的到达每个锚节点的跳数和平均每跳距离,计算出到达每个锚节点的距离.
5) 未知节点根据与每个锚节点的距离和锚节点的坐标值,利用最小二乘法计算其自身坐标.
1.2 DV-hop算法存在的问题在DV-hop算法中,采用锚节点之间的平均每跳距离作为未知节点到锚节点的平均每跳跳距,通过每跳跳距与跳数的乘积来表示未知节点和锚节点之间的距离. 因此DV-hop定位算法对跳数具有很强的依赖性,当锚节点因为种种原因接收不到准确合理的跳数值时,将对平均每跳距离值的计算造成很大的影响,未知节点的位置确定也就随之产生很大的变化.
1.3 现有的改进方法简述DV-hop算法不依赖于测量误差,简单易行,但由于定位精度不高,研究者们提出了很多改进方法,降低定位误差. 吴凌飞等提出将DV-hop算法与RSSI算法相融合,将位于信标点一跳以内的节点采用RSSI辅助定位算法估计,对于一跳以外的节点采用经典DV-hop算法估计[6]. 为了充分考虑锚节点之间以及锚节点与未知节点之间的拓扑关系,基于共线性方法的DV-Hop算法被提出来[7]. 跳数的精确性作为影响定位精度的重要因素,基于跳数比的DV-Hop算法也随之产生. 但是这些方法有些需要增加硬件,有些程序过于复杂. 为了节约能源,提高无线传感器网络定位节点的精确性,根据两点的覆盖面积的比例引入了一个跳数系数,精确跳数的数值,可更为简单、方便地降低传感器节点的定位误差.
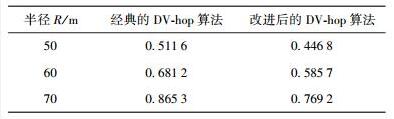
2 改进的DV-hop定位算法 2.1 改进算法的思想在通信范围内,在计算时不论多远其跳数都被记为一跳,这在一定程度上偏离了实际距离. 如图 1所示,R为O点的通信半径. 根据DV-hop算法,在其通信范围内,O点与A、B、C3点的通信都被记为一跳,但实际上,只有与C点的通信接近于真实值一跳,而A、B具有相对较大的定位误差.
|
图 1 O点的通信范围节点分布 |
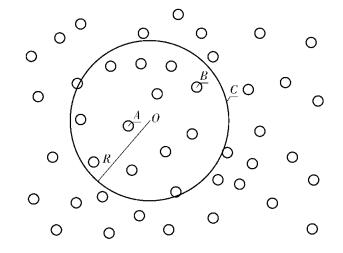
如图 2所示,在B点的一跳通信范围内,到达O点一部分节点需要一跳,另一部分节点需要2跳. 将需要2跳到O点的节点数与B点可覆盖的总节点数的比值作为依据,寻找规律,得到一个跳数系数,精确一跳的数值,从而降低平均每跳距离值的误差,使未知节点的位置确定更为准确.
|
图 2 O点、B点通信范围节点分布图 |
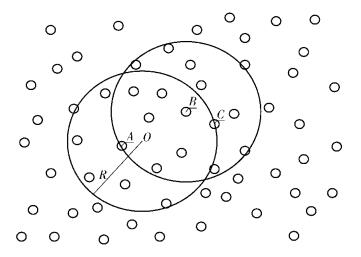
如图 3所示,R的距离为一跳,跳数系数为1,则O点到B点的距离可被看作更新的跳数系数x. 已知B点的覆盖范围内,O点不能覆盖的节点在P月牙区域内,节点总数为y. B点能覆盖的范围内节点总数为z.
|
图 3 B点的跳数系数调整图 |
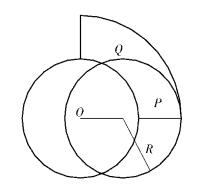
节点数y、z的比值可用区域P与以B点为中心R为半径的圆的面积的比值所表示. 由于月牙区域P不容易计算,将P近似为区域Q(1/4的同心圆环),则y、z比值的计算式为
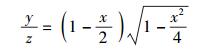
|
(2) |
与经典的DV-hop算法基本一致,首先通过泛洪获得各节点之间的跳数. 与此同时,每个节点需要保存关于前一节点的3个参数:前一节点的标号,前一节点未能覆盖而本节点能覆盖到的节点总数,以及通信范围内可覆盖到的节点总数.
1) 每个节点记录自身与邻居节点的数据.
① 发起节点i将自身的表值加入DV-hop数据包中,并转发出去.
② 收到数据包的节点j保存收到的值. 当节点j向邻居节点通信时进行分析. 若节点j能覆盖到的节点而节点i覆盖不到,系数y(y初始值为0)加1. 节点j记录自身能覆盖到的节点,记为系数z(z初始值为0).
2) 与经典DV-hop算法一致,每个未知节点得到到锚节点的最短路径,更新跳数.
① 从对锚节点跳数为1的节点开始,利用式
(2)计算跳数系数x,将跳数系数乘以跳数,更新跳数值.
(2) 计算跳数系数 x,将跳数系数乘以跳数,更新跳数值.
② 节点i根据前一节点更新的跳数加上自身到前一节点更新的跳数,获得最终的跳数.
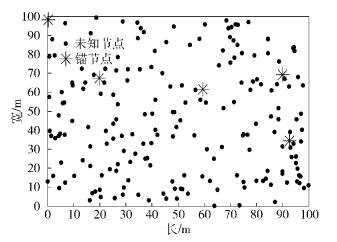
3 实验仿真及结果分析仿真分析的网络环境设置:利用Matlab对实验进行仿真,设置200个传感器节点随机均匀分布在100m×100m正方形区域内,5个锚节点,研究在不同的通信半径(R)与参考节点比例条件下节点定位的性能.
设实际位置为(Xi,Yi),估计位置为(xi,yi),未知节点总数为u(未知节点数等于节点总数减去锚节点数),网络仿真时节点i的定位误差ei、200个未知节点的平均定位误差er及归一化后的平均定位误差av分别为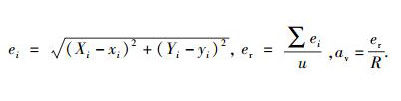
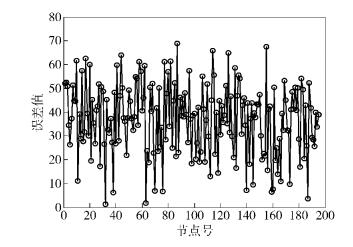
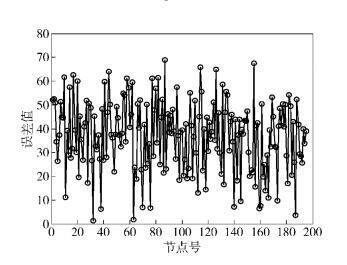
图 4~图 6分别给出了节点通信半径为70m时,传感器节点的分布图、经典DV-hop算法的节点定位误差图和改进DV-hop算法的节点定位误差图. 在图 5和图 6中,横坐标表示节点序号,纵坐标表示每个节点定位误差数值. 比较图 5和图 6可以看出,改进DV-hop算法显著优于经典DV-hop算法. 经过修改调整后的跳数使节点误差明显减小,经典DV-hop算法误差从90~180的部分均被减弱. 200个未知节点的平均定位误差er,经典算法为58.678 6 m,改进后的算法所得数值为43.203 2 m.
|
图 4 节点分布 |
|
图 5 经典DV-hop算法的节点定位误差 |
|
图 6 改进DV-hop算的节点定位误差 |
将200个未知节点对通信半径归一化的平均定位误差经过30次运算,取均值. 如表 1所示,通信半径越大,在同一区域内跳数误差率越高,最后定位结果误差越大. 不论半径是50 m、60 m、70 m,改进后的DV-hop算法都能使未知节点的定位误差减小. 改进后的DV-hop算法与经典的DV-hop算法相比,节点归一化的平均定位误差大约降低了10%.
|
|
表 1 未知节点对通信半径归一化后的平均定位误差 |
为了提高DV-hop算法在随机分布传感器网络中的定位性能,调整改进了算法中的跳数. 利用两点间的覆盖关系,得到一个跳数系数,使改进的DV-hop算法的结果比经典的DV-hop算法的结果更接近于真实值,在一定程度上降低了DV-hop算法的误差. 从仿真结果可以看出,改进后的算法在定位精度上确实有所提高,且对于各个节点通信半径下皆可适用,具有一定的实用性,是节点定位的可选方案.
DV-hop定位算法更加适用于锚节点分布均匀、各向同性、密集型的无线传感器网络,在这种情况下求得的平均每跳距离值才能更接近实际距离值. 算法依旧依赖于邻居节点分布的均匀性、各向同性和密集性. 当节点密集分布时,网络中节点间的多跳路径距离更接近实际距离. 当节点稀疏分布时,节点的覆盖比例很不匀称,改进算法也将不能起到应有的作用,这样计算的距离值会产生较大的累积误差,这是进一步研究的重点问题.
| [1] | Akyildiz I F, Su Weilian. A survey on sensor networks[J]. IEEE Communications Magazine, 2002, 40(8): 104–112. |
| [2] | Dragos Niculescu, Badri Nath. DV based positioning in ad hoc networks[J]. Telecommunication Systems, 2003, 22(1): 267–280. |
| [3] | Niculescu D, Nath B. Ad hoc positioning system (APS) using AoA[C]//Proceedings of IEEE INFOCOM 2003. San Francisco: IEEE Computer and Communications Societies, 2003: 1734-1743. |
| [4] | Sayed A H, Tarighat A, Khajehnouri N. Network-based wireless location: challenges faced in developing techniques for accurate wireless location information[J]. IEEE Signal Processing Magazine, 2005, 22(4): 24–40. doi: 10.1109/MSP.2005.1458275 |
| [5] | Yu Weiqi, Li Hao. An improved DV-hop localization method in wireless sensor network[C]//2012 IEEE International Conference on Computer Science and Automation Engineering. Zhangjiajie: IEEE Press, 2012: 25-27. |
| [6] | Liu Ying, Qian Zhihong, Liu Dan, et al. A DV-hop positioning algorithm for wireless sensor network based on detection probability[C]//2009 Fifth International Joint Conferences on INC, IMS and IDC. Seoul: International Joint Conferences, 2009: 453-456. |
| [7] | Wu Lingfei, Liang Huawei, Lin Zijing, et al. An improvement of DV-hop algorithm based on collinearity[C]//Proceedings of the 2009 IEEE International Conference on Information and Automation. Zhuhai: [s. n. ], 2009: 90-95. |