2. 中国电子科技集团公司第五十四研究所, 石家庄 050081;
3. 西安应用光学研究所, 西安 710071
针对多径衰落信道中幅相调制信号的类型识别问题, 提出了一种基于自适应马尔可夫链蒙特卡洛 (MCMC)——自适应Metropolis的改进算法.该算法利用Markov链的历史信息自动调整建议分布函数的协方差矩阵, 使其不断地逼近目标分布, 从而避免了传统Metropolis算法中建议分布函数选取这一难题, 并能有效地提高采样效率.仿真实验表明, 算法具有很好的识别精度, 证明了算法的有效性.
2. The No.54 Research Institute of CETC, Shijiazhuang 050081, China;
3. Xi'an Institute of Applied Optics, Xi'an 710065, China
A new algorithm based on adaptive Metropolis algorithm for recognizing phase-amplitude-modulated signals in multipath fading channel was proposed. The method uses the full history of the chain to tune covariance of the proposal distribution adaptively. This adaptation strategy can approach an approximation of the target distribution, which can avoid the problem of selecting proposal distribution in traditional Metropolis algorithm and improve the sampling efficiency effectively. Simulation show that the proposed method has high accuracy which verifies the validity of the algorithm.
通信信号调制识别广泛应用于军事和民用通信方面.目前,绝大部分调制识别算法的研究都是针对理想高斯信道[1-3],但在实际通信系统环境下,由传输路径的多径反射以及接收机的同步定时误差和不完全匹配滤波引起的码间干扰不可避免,因此,如何在多径衰落信道环境中实现信号的调制识别成为该领域研究的热点和难点[4-5].近年来,马尔可夫链蒙特卡洛方法以其高度的灵活性和超强的功效性,引起了信号处理领域的极大关注.目前,已有学者采用Metropolis-Hastings (MH) 算法实现多径信道下的调制类型识别[6],但其中对算法性能起决定作用的建议分布函数的选取至今仍是难题.笔者提出一种基于自适应Metropolis (AM, adaptive Metropolis) 的调制识别算法,利用Markov链的历史信息自动优化建议分布函数,在保持良好遍历性的同时提高了识别效率.
1 最大似然调制识别在多径衰落信道中,接收信号的复基带形式为
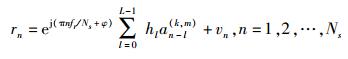
|
(1) |
其中:{an(k, m)}为选自第k个功率归一化的标准星座A(k)={a(k, 1), …, a(k, Mk)}(k=1, 2, …, K) 的第m个码元,Mk为该星座中的星座点个数;h=[h0, …, hL-1]为信道冲击响应系数向量,L为信道多径阶数;归一化残留载波频率和相偏分别记为fr和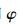
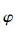
基于最大似然理论的调制识别算法可被视为一个多元假设检验问题:
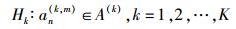
|
根据广义似然比 (GLRT, general likelihood ratio test) 理论,在噪声建模为高斯分布的假设下,第k种假设的条件似然函数可表示为
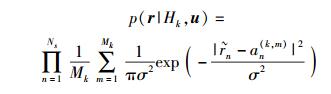
|
(2) |
其中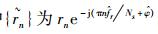
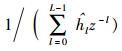
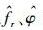
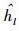
近年来,起源于统计物理学的马尔可夫链蒙特卡洛 (MCMC, Markov chain Monte Carlo) 方法[7]引起了信号处理领域的极大关注,其核心思想是产生一个以目标概率密度函数为稳定分布的各态历经的Markov链,并以该链达到稳态时的样本作为目标分布的样本,成功解决了贝叶斯分析中异常复杂的数值计算问题.
根据贝叶斯理论,很容易得到
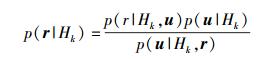
|
(3) |
由重要采样理论可知,式 (3) 可由式 (4) 近似得到.
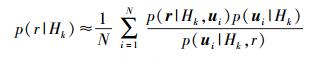
|
(4) |
其中:ui由对目标分布函数p(u|Hk, r) 采样得到,N为用于式 (3) 的近似估计的采样点的个数.由于未知参数向量u的先验概率不依赖于假设Hk,因此概率函数可简化为p(ui|Hk)=p(ui).采样点的遍历性保证了在采样个数N→∞的情况下,式 (4) 的数值无限接近于p(r|Hk).因此产生服从目标分布p(u|Hk, r) 的采样点是MCMC分类器的关键.
AM算法[8]是Haario在2001年提出的一种全局自适应调整策略,是在经典随机游走Metropolis算法的基础上提出的,其基本思想是首先构建高斯建议分布函数,然后利用Markov链样本校正高斯分布的协方差矩阵.与传统MH算法相比,AM算法不需要预先确定参数的建议分布函数,而是利用Markov链的全部历史信息自适应地调整建议分布函数,这种调整会改变建议分布函数的延展度和空间方向,使其不断地逼近目标分布函数,从而有效提高采样效率.
假设已抽取采样点u0, u1, …, ui,下一个待选采样点w由建议分布函数qi(·|u0, u1, …, ui) 中抽取产生,并且w的接受概率为
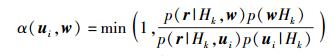
|
(5) |
下一个采样点以概率α(ui, w) 被设置为ui+1=w,以概率1-α(ui, w) 保持前一采样点的值不变,即ui+1=ui. AM算法中的建议分布函数就是均值为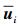
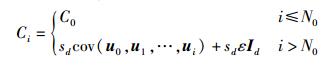
|
(6) |
其中:参数sd仅取决于未知参数向量ui的维数d;ε>0为一个非常小的数,它的存在是为了保证Ci在迭代过程中的非奇异性;Id为d阶单位阵.为了减少计算协方差矩阵过程中的计算开销,Ci可以根据递归表达式 (7) 计算得到.
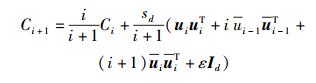
|
(7) |
其中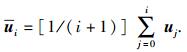
综上所述,AM算法调制识别算法的计算流程如下.
步骤0 (初始化) 任意选取初始状态u0及初始协方差矩阵C0,设置i=0.
步骤1 采用下列步骤生成ui+1.
1) 根据式 (7) 计算Ci.
2) 产生服从正态分布的待选采样点w~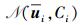
3) 产生服从均匀分布的随机数λ~U(0, 1),根据式 (5) 计算待选采样点w的接受概率.若λ≤α(ui, w),则接受ui+1=w,否则ui+1=ui.
步骤2 重复步骤1,直到产生足够多的采样值可以满足计算式 (4) 的要求.
步骤3 对于每一种可能的调制样式假设Hk(k=1, 2, …, K),重复步骤0~步骤2.比较每种假设下的似然函数值p(r|Hk),判定使似然函数达到最大者为真.
3 仿真结果与分析假设待选择的调制样式包括BPSK、4PAM、8PSK、16QAM,且各种调制样式先验等概率.频偏、相偏和多径系数均统计独立,则p(u|Hk) 可表示为
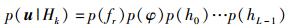
|
其中:fr和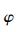
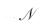
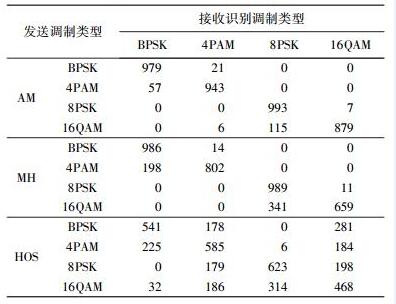
表 1给出了分别采用AM算法、MH算法[6]及HOS算法[4]进行1 000次试验的统计结果.其中,Ns=250,信噪比为5 dB,fr=0.2,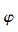
|
|
表 1 3种算法分类性能的比较 |
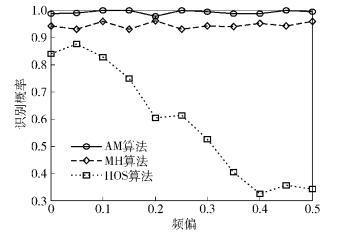
图 1给出了在信噪比为5 dB、观测码元个数Ns=250条件下,载波频偏分别对3种算法分类性能的影响,其中fr的变化范围为0~0.5,其余参数设置为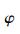
|
图 1 3种算法的正确识别概率随频偏变化的曲线 |
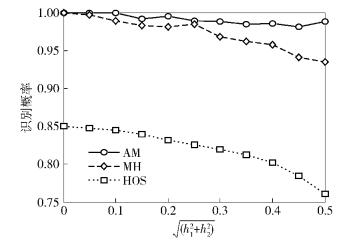
图 2给出了在信噪比为5 dB、观测码元个数Ns=250条件下,信道响应系数分别对3种算法分类性能的影响.以3阶多径信道为例,其中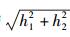

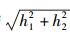
|
图 2 3种算法的正确识别概率随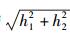 |
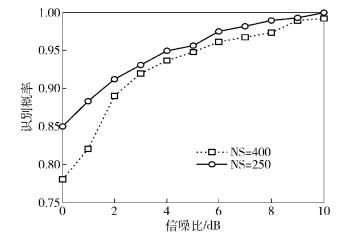
图 3所示为在观测码元个数分别为250和400时,应用所提出的AM算法对4种信号进行识别的正确识别概率随信噪比变化的曲线.其中,fr=0.2,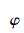
|
图 3 AM算法的正确识别概率随信噪比变化的曲线 |
最后考查算法的计算复杂度,这里主要对AM和MH算法的复杂度进行分析比较.由于这2种算法中均含生成服从某一分布随机数的过程,而计算机在处理该问题时采用不同的方法会导致不同的计算复杂度表达式,因此无法对复杂度进行定量描述.这里采用在相同计算机上的算法运行时间作为参考对算法复杂度做定性分析.表 2列出了分别采用AM和MH算法生成一次未知参数样本所消耗的时间,其中Ns=200.可以看出,AM算法较MH算法的复杂度略有增加,这是自适应更新建议分布函数带来的计算开销,但由于在计算建议分布函数的协方差矩阵时采用式 (7) 的递推公式,使得自适应算法引入的计算复杂度在可以承受的范围之内.
|
|
表 2 2种算法计算时间的比较s |
提出了一种基于AM的调制识别算法,该算法避免了建议分布函数选取这一难题,在迭代过程中利用Markov链的历史信息自动调整建议分布函数,因此能有效地提高采样效率.仿真结果表明,所提算法识别效果优于MH算法以及HOS算法,证明了该算法的有效性.
| [1] | Dobre O A, Abdi A, Bar-Ness Y, et al. Survey of automatic modulation classification techniques: classical approaches and new trends[J]. IET Communications, 2007, 1(2): 137–156. doi: 10.1049/iet-com:20050176 |
| [2] | Popescu D C, Dobre O A, Hameed F. On the likelihood-based approach to modulation classification[J]. IEEE Transactions on Wireless Communications, 2009, 8(12): 5884–5892. doi: 10.1109/TWC.2009.12.080883 |
| [3] | Xu J L, Su Wei, Zhou Meng Chu. Likelihood-ratio approaches to automatic modulation classification[J]. IEEE Transactions on System. Man and Cybernetics, 2011, 41(4): 455–469. doi: 10.1109/TSMCC.2010.2076347 |
| [4] | Wu H C, Saquib M, Yun Z F. Novel automatic modulation classification using cumulant features for communications via multipath channels[J]. IEEE Trans Wireless Communications, 2008, 7(8): 3198–3105. |
| [5] |
李鹏, 汪芙平, 王赞基. 时变多径信道中通信信号调制识别算法[J]. 清华大学学报, 2007, 47(7): 1097–1100.
Li Peng, Wang Fuping, Wang Zanji. Algorithm for modulation recognition in a time-variant multipath channel environment[J]. Journal of Tsinghua University, 2007, 47(7): 1097–1100. |
| [6] | Lesage S, Tourneret J Y, Djuric P M. Classification of digital modulations by MCMC sampling[J]. IEEE ICASSP, 2001: 2553–2556. |
| [7] | Chib S, Greengerg E. Understanding the Metropolis-hastings algorithm[J]. American Statistician, 1995, 49(4): 327–335. |
| [8] | Haario H, Saksman E, Tamminem J. An adaptive Metropolis algorithm[J]. Bernoulli, 2001, 7(2): 223–242. doi: 10.2307/3318737 |