2. 遵义医学院 医学信息工程系, 贵州 遵义 563003
提出了一种优化循环转移矩阵偏量候选集合的结构化准循环低密度奇偶校验(QC-LDPC)码构造算法.通过研究基矩阵与校验矩阵之间环的关系, 达到了减少QC-LDPC码校验矩阵中短环数量和围长最大化的目的.仿真结果表明, 基于该算法构造的QC-LDPC码的短环数量明显减少, 围长至少可以达到6或8,误码率性能均得到了不同程度的提升.
2. Department of Medical Information Engineering, Zunyi Medical College, Guizhou Zunyi 563003, China
A construction algorithm with optimized shift value of circulant permutation matrix for quasi-cyclic low-density parity check (QC-LDPC) codes was presented. Through analyzing the cycle relationships between the basis matrix and the check matrix, the number of short cycles was reduced and the girth of check matrix in QC-LDPC code was maximized. The simulation results show that the girth of QC-LDPC codes constructed by proposed algorithm could at least extend to 6 or 8, while the number of short cycles was decreased significantly. In the end, the bit error rate performance was effectively improved.
QC-LDPC码实现的关键是如何针对应用参数设计性能良好的校验矩阵.而一个性能良好的校验矩阵必须保证其相应的Tanner图具有最大围长(校验矩阵中最小环长)、最少短环数量和最大短环连通度等优点. PEG(progress edge growth)[1-3]算法在使QC-LDPC码校验矩阵相应Tanner图围长最大时,其基矩阵的每个循环转移矩阵均存在多个候选偏移量. ACE (approximate cycle extrinsic message degree)[4-6]可以提高短环的连通度,也优化了文献[1]和文献[2]中每个循环转移矩阵的候选偏移量,但同样存在多个候选偏移量满足同一个ACE值的情况. EMD(extrinsic message degree)[7-8]值可以再一次提高短环的连通度,同时也对相同ACE值的循环转移矩阵候选偏移量进行了优化.
为进一步优化循环转移矩阵偏移量候选集合,缩小候选集合范围,使得QC-LDPC码围长最大,减少短环的数量.笔者通过研究基矩阵和校验矩阵之间环的关系,提出了一种优化循环转移矩阵偏移量集合(OSV,optimized shift value of circulant permutation matrix)的QC-LDPC码构造算法.
1 循环转移矩阵优化理论推导 1.1 QC-LDPC码定义QC-LDPC码可以由一个J×L的基矩阵定义:
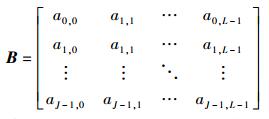
|
(1) |
其中:aj, l代表一个p×p的循环转移矩阵,aj, l=0代表单位矩阵,aj, l>0代表循环转移单位矩阵的偏移量,aj, l=-1代表p×p零矩阵.基矩阵的每一列和每一行分别代表Tanner图中的变量节点Vl(0≤l≤L-1) 和校验节点Cj(0≤j≤J-1).
1.2 QC-LDPC码环的性质基矩阵中一条长为2l的路径:

|
(2) |
当j0=jl,jk≠jk+1,lk≠lk+1时,可形成一条长为2l的环. Fossorier [9]指出校验矩阵中存在一条长为2l的环的充分必要条件为
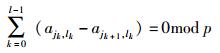
|
(3) |
其中:j0=jl,jk≠jk+1,lk≠lk+1.由以上所述可知,基矩阵中一条长为2l的环,当满足式(3) 时,可在校验矩阵H中形成一条长为2l的环;当不满足式(3) 时,可在校验矩阵H中形成一条环长大于2l的环.这一结论可描述为以下的定理1.
定理1 基矩阵中存在一条关于循环转移矩阵ajk, lm长为LBajk, lm=2l的环,p表示基矩阵中循环转移矩阵的阶数,s表示循环转移矩阵总偏移量:
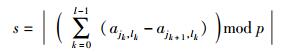
|
(4) |
其中:j0=jl,jk≠jk+1,lk≠lk+1,0≤s≤p.则在校验矩阵H中可形成一条长为LHajk, lm=n×2l的环,其中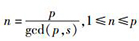
通过定理1可以定量地计算出LBajk, lm=2l在校验矩阵H中所形成的环的长度为LHajk, lm.但是,由于校验矩阵H是将基矩阵中每一个元素用一个p×p的循环转移矩阵替代而得到的,因此环长为LHajk, lm的环并不唯一.为进一步计算校验矩阵H中环长为LHajk, lm的环的个数,通过定理1得到推论1.
推论1 假设QC-LDPC码基矩阵中存在一条长为H中环长为LBajk, lm=2l的环,相应校验矩阵H中存在一条长为H中环长为LHajk, lm=n×2l的环,该环的个数Cajk, lm=gcd(p, s),1≤Cajk, lm≤p.
在对基矩阵进行完全树展开的过程中,每一层均遍历了与当前层每一个节点的相关节点,因此,在统计短环数量时,推论1仅可以精确地计算环长分别为4和6的短环的数量,当环长超过8时将存在以下几种特殊结构的环,定义分别如下:
定义1 当LHajk, lm≥8并且LHajk, lm是LBajk, lm的整数倍时,假如基矩阵中存在LBajk, lm=2l的路径:
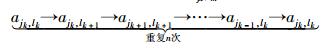
|
(5) |
将式(5) 重复n次,且根据式(4) 有smod p=0,则可形成长为LHajk, lm=n×2l的环,称LHajk, lm=n×2l的形成过程为小环形成大环.
定义2 当LHajk, lm≥8时,假如基矩阵中存在以下路径:
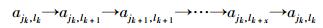
|
(6) |
其中部分节点重复多次而不能形成闭环,x为任意大于0的正整数,该路径称为病态环.
定义3 当LHajk, lm≥8时,假如存在以下路径:
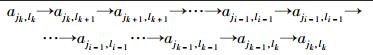
|
(7) |
其中部分节点重复多次形成闭环,但环长小于当前路径长度,当路径ajj-1, li-1→aji-1, li-1→…→aji-1, li-1的smod p=0时,称该路径为环中环.
通过上述定义可知,为精确统计LHajk, lm≥8的环的数量,应将小环形成大环的环统计在内,而避免统计病态环和环中环,从而得到以下关于循环转移矩阵偏量集合的定理2.
定理2 基矩阵中存在一条长为LBajk, lm=2l的环,该环所包含的循环转移矩阵集合为
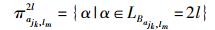
|
(8) |
则与ajk, lm相关的偏移量候选集合为
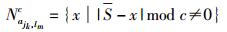
|
(9) |
其中:S为循环转移矩阵偏移量的部分和,S=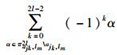
QC-LDPC码构造可以分为2个步骤:通过IPEG (improved progressive edge growth)[6]算法构造如式(1) 所定义的基矩阵;确定基矩阵中各循环转移矩阵的偏移量.
基矩阵构造完后,确定基矩阵中循环转移矩阵的偏移量.可以通过取循环转移矩阵在校验矩阵中各环长候选集合的交集,达到缩小偏移量候选集合的目的,即
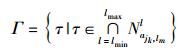
|
(10) |
其中lmin和lmax分别为与当前循环转移矩阵ajk, lm相关的最小环长和最大环长集合.根据以上分析,优化方法的实现步骤如下:
1) 通过变量节点Vi的度分布di逐个确定基矩阵循环转移矩阵的偏移量;
2) 随机从0~p个正整数中选取一个数值作为变量节点Vi第1个循环转移矩阵的偏移量;
3) 确定变量节点Vi第k个循环转移矩阵Vik的偏移量时,对Vik进行完全树展开,共展开l层,然后,根据定理1逐层查找与节点Vik相关的环,并根据式(8) 计算得到集合πVik2l;
4) 根据式(9) 计算出与集合πVik2l中每个环长相关的偏移量候选集合NVikc;
5) 根据式(10) 求得所有环候选集合的交集Γ;
6) 如果Γ=Φ,去掉NVikc中最大环长的候选集合返回5),直到Γ≠Φ为止;
7) 根据推论1计算6) 中最大环长的数量CVik;
8) 返回3) 直到Vik所有节点处理完成;
9) 返回1) 直到所有变量节点Vi处理完成.
3 基于OSV算法性能试验仿真过程中调制方式采用BPSK,信道模型为AWGN,置信译码算法最大迭代次数设为30.当错误帧达到100或达到最大迭代次数时,BP译码算法停止.
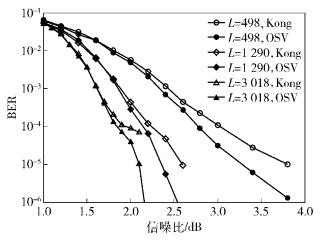
首先测试OSV算法构造一组(3, 6) 规则码,码率R为1/2,码长L分别为498、1 290和3 018,循环转移矩阵的阶数分别为83、215和503,然后将OSV算法和Kong等[10]所构造的QC-LDPC码进行误码率(BER, bit error rate)性能对比,结果如图 1所示.
|
图 1 (3, 6) 规则码,不同码长时QC-LDPC码BER的性能对比 |
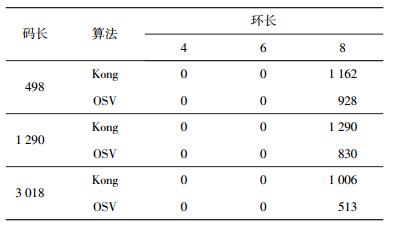
由图 1可知,在低信噪比时,OSV算法的BER与Kong等算法的BER性能相当,但随着信噪比的提升,OSV算法的BER性能明显优于Kong等算法.这是由于OSV算法优化了校验矩阵的短环结构,去除了短环. OSV算法和Kong等所构造的QC-LDPC码的短环统计情况见表 1.
|
|
表 1 码率R=1/2时(3, 6) 规则QC-LDPC码的环数统计 |
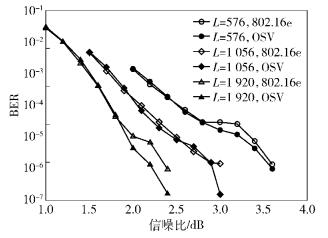
为进一步验证OSV算法构造不规则码的性能,下一组实验选择了802.16e所推荐的一组码率R=1/2,码长L分别为576、1 056和1 920,基矩阵除数为12×24,基矩阵中循环转移矩阵阶数分别为24、44和80的QC-LDPC码不规则码进行重新构造,度分布同802.16e一样. OSV算法同802.16e相同码的BER性能比较如图 2所示.同时,环长为4、6和8的短环统计情况见表 2.
|
图 2 不规则码,不同码长,码率R为1/2时的BER性能对比 |
|
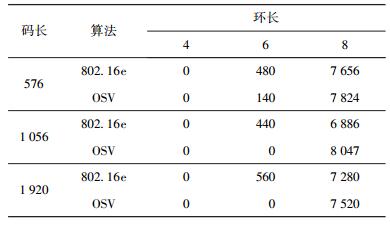
|
表 2 码率R=1/2时不规则QC-LDPC码的环数统计 |
由表 2可以看出,当码长为576时,OSV算法仅去除了长为4的环,减少了长为6的环的数量,OSV算法的BER性能略微优于802.16e(见图 2).但当码长为1 056和1 920时,OSV算法去除了所有长为4和6的环,使得围长达到了8,并且随着信噪比的提升,OSV算法的EBR性能优于802.16e.
4 结束语经过理论分析,建立了QC-LDPC码基矩阵和校验矩阵之间环的关系,以此为依据,提出了一种优化循环转移矩阵偏移量集合的结构化QC-LDPC码构造算法,即OSV算法.通过合理地选择循环转移矩阵偏移量,使QC-LDPC码校验矩阵的短环数量减少,围长最大.仿真结果表明,根据OSV算法构造的QC-LDPC码,无论是规则码还是不规则码,其性能都得到了不同程度的提升.
| [1] | Huang Liqun, Wang Yuliang, Gong Ping. An improved construction method of QC-LDPC codes based on the PEG Algorithm [C]//PACCS 2011. China: IEEE Press, 2011: 1-4. |
| [2] | Fan Zhiyong, Zhang Weibo, Liu Xingcheng, et al. An improved algorithm for constructing QC-LDPC codes based on the PEG algorithm [C]//ChinaCOM 2009. China: IEEE Press, 2009: 1-4. |
| [3] | Hu Xiaoyu, Eleftheriou E, Arnold D M. Regular and irregular progressive edge-growth tanner graphs[J]. IEEE Transactions on Information Theory, 2005, 51(2): 386–398. |
| [4] | He Huan, Xu Youyun, Cai Yueming. Irregular quasi-cyclic LDPC codes design with generalized ACE constraint [C]//2009 International Conference on Communications and Mobile Computing. China: IEEE Press, 2009: 196-199. |
| [5] | Li Jilong, Di Na, Yang Ming, et al. Construction of quasi cyclic LDPC with ACE constraint [C]//WCNIS 2010. China: IEEE Press, 2010: 90-93. |
| [6] | Xiao Hua, Amir H Banihashemi. Improved progressive-edge-growth (PEG) construction of irregular LDPC codes[J]. IEEE Communications Letters, 2004, 8(12): 715–717. doi: 10.1109/LCOMM.2004.839612 |
| [7] | Myung S, Yang K, Kim J. Quasi-cyclic LDPC code construction with low error floor based on the IPEG algorithm[J]. IEEE Communications Letters, 2007, 11(7): 607–609. doi: 10.1109/LCOMM.2007.061650 |
| [8] | Tian Tao, Jones C, Villasenor J D, et al. Selective avoidance of cycles in irregular LDPC code construction[J]. IEEE Transactions on Communications, 2004, 52(8): 1242–1247. doi: 10.1109/TCOMM.2004.833048 |
| [9] | Fossorier M P C. Quasi cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788–1793. doi: 10.1109/TIT.2004.831841 |
| [10] | Kong Lingjun, Yang Xiao. Ruling out small stopping sets and small girth in Tanner graph of QC-LDPC[J]. Journal of Systems Engineering and Electronic, 2010, 21(1): 134–137. doi: 10.3969/j.issn.1004-4132.2010.01.021 |