对无迹卡尔曼滤波(UKF)算法进行了改进,提出一种双重自适应UKF算法.该算法能缩放噪声、平抑模型噪声;通过监测基于新息特性的自适应矩阵的迹并进行实时修改,达到抑制观测干扰的目的.仿真结果表明,双重自适应UKF算法对于模型噪声和观测干扰十分敏感,同时具有较强的鲁棒性,能快速对其进行平抑.
An improved unscented Kalman filter (UKF) algorithm is called dual adaptive UKF. It could not only stabilize model noise by the method of resizing noise, but also inhibit observation interference by monitoring the trace of the adaptive matrix based on innovation characteristics and amending the adaptive matrix in time. Simulation results show that the dual adaptive UKF algorithm is very sensitive to model noise and observation interference. And it has strong robustness which could stabilize the model noise quickly.
初始对准是捷联式惯性导航系统(捷联惯导系统)(SINS, strapdown inertial navigation system)的关键技术之一,它直接影响捷联惯导系统的导航性能.笔者主要研究初始对准中的动基座对准.
UKF在进行捷联惯导系统动基座初始对准中有着非常广泛的应用.为了改进初始对准的精度和速度,改进UKF算法是一个重要的研究方向[1-2].提出了一种双重自适应UKF,以达到平抑模型噪声和抑制观测干扰的目的.仿真结果显示,提出的双重自适应UKF具有较强的鲁棒性且能较快地抑制模型噪声和观测干扰.
1 传递对准滤波模型主要研究动基座对准中的传递对准方法,并使用较为成熟的“速度匹配”方案.它可以较快地估计失准角并具有相当的精度,且在遇到弹性变形时所受到的影响很小.
SINS误差模型是初始对准的基础.根据具体的初始对准条件、假设和约束,SINS误差模型就可以简化为对准误差模型.取初始对准的导航坐标系为东北天(ENU, east-north-up)当地地理坐标系.系统状态矢量为
|
其中:ΦE、ΦN、ΦU为东、北、天3个方向的平台失准角;δvE、δvN、δvU为东、北、天3个方向的速度误差;qx、qy、qz为陀螺仪随机常数;θx、θy、θz为陀螺仪一阶马尔可夫过程;ρx、ρy、ρz为加速度计一阶马尔可夫过程.
已知捷联惯导系统的误差模型[3]
|
(1) |
|
(2) |
|
(3) |
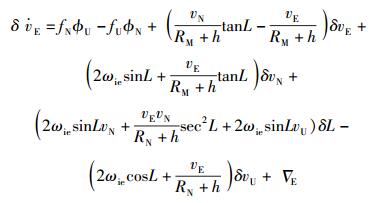
|
(4) |
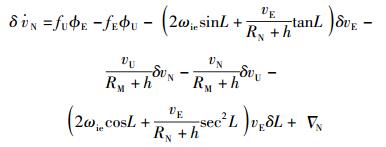
|
(5) |
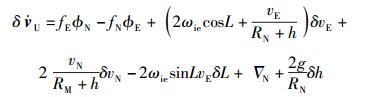
|
(6) |
其中:vE、vN、vU为东、北、天3个方向的速度,εE、εN、εU为东、北、天3个方向陀螺仪噪声,RM为地球子午圈半径,RN为地球卯酉圈半径,L为当地纬度,ωie为地球自转角速度,h为当地海拔高度,fE、fN、fU为东、北、天3个方向的比力输出,∇E、∇N、∇U为东、北、天3个方向的加速度计测误差.
系统的观测方程
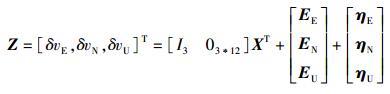
|
(7) |
其中:Z是观测矢量;[EE, EN, EU]T为系统观测干扰矢量,[ηE, ηN, ηU]T为系统观测噪声矢量.
2 UKF算法文献[4]提出了UKF.它以无迹变换(UT, unscented transformation)为核心,以卡尔曼滤波器为框架.其中最为常见的是采用尺度可变对称采样策略的UKF算法,其流程如下[4],并如图 1所示.
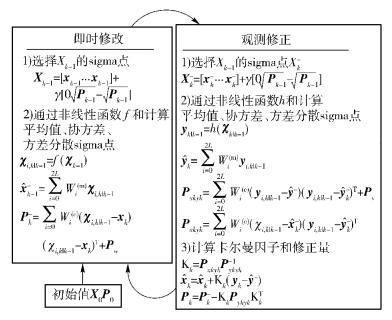
|
图 1 UKF算法流程示意图 |
1) UKF滤波器的权重因子W及相关参数
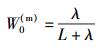
|
(8) |
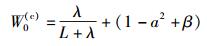
|
(9) |
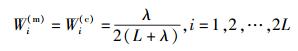
|
(10) |
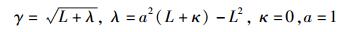
|
(11) |
其中:γ、λ都是尺度参数;常量a描述了采样点的分布范围,通常取10-4 < a < 1;κ为二阶尺度参数,常取为0;β用于体现变量先验分布信息,高斯分布下常取β=2.
2) 初始化及构造sigma点集
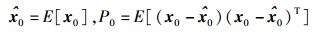
|
(12) |
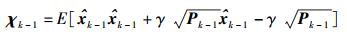
|
(13) |
其中: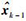
3) 状态更新
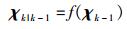
|
(14) |
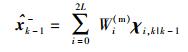
|
(15) |
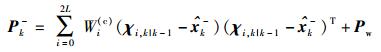
|
(16) |
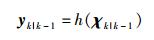
|
(17) |
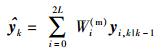
|
(18) |
4) 观测更新
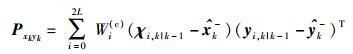
|
(19) |
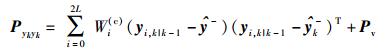
|
(20) |
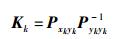
|
(21) |
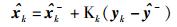
|
(22) |
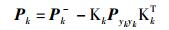
|
(23) |
初始对准模型可抽象为如下系统:
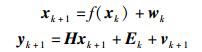
|
其中:f(·)代表非线性状态转移,H代表观测矩阵;w和v分别代表模型噪声和观测噪声;x∈Rn代表状态量;y∈Rm代表观测输出;Ek代表未知干扰的分布函数.
下面从模型噪声自适应和观测干扰自适应2个方面同时对UKF进行改进.
3.1 对模型噪声进行自适应缩放的方法滤波算法中预测残差的序列,即新息(innovation)协方差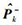
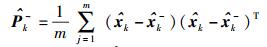
|
和计算的新息协方差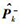
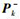
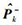
而观测方程中产生的新息
|
(24) |
在最优滤波的情况下,dk是期望为0的高斯白噪声序列,式(24) 两端开窗取方差得
|
(25) |
该式可以作为模型噪声方差的估计依据,引入以下缩放因子[5]
|
(26) |
所以,模型噪声方差的缩放可用如下公式处理,同时达到平滑的效果
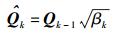
|
(27) |
定义观测值和滤波值的残差为
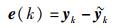
|
(28) |
式中:yk表示观测值,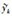
胡迪等[6]认为,当滤波结果无偏时,e(k)方差的开窗均值满足
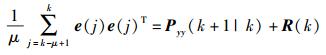
|
(29) |
其中:μ表示滚动窗口的大小,Pyy表示观测估计方差,R表示观测噪声方差.
可定义自适应矩阵为
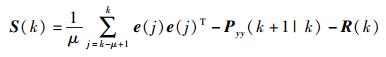
|
(30) |
S(k)的迹的统计特性服从χ2分布,通过检测S(k)的迹可以得知非正常值是否存在[6]
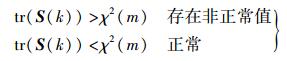
|
(31) |
其中m一般情况代表观测变量的个数,但在大数据量且统计标准并不明确的情况下,上述方法误差较大,所以笔者提出一种新的判决门限,自适应地判别每一次滤波后自适应矩阵迹的门限,提高准确度.
设Z1, Z2, Z3, …, Zk是来自正态总体N(μ, σ2)的一个样本,其无偏方差为
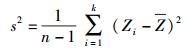
|
(32) |
根据χ2分布的性质,有
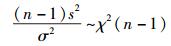
|
(33) |
其中Z为样本均值.另外,χ2分布上侧α分位数定义为:对给定的正数α,0 < α < 1,满足条件
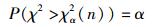
|
(34) |
的数χα2(n),称为χ2(n)分布的上侧α分位数. χα2(n)是一个只与自由度n和概率α有关的函数.
依据χ2分布性质,将式(32) 代入式(33),得
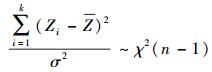
|
(35) |
式中方差σ2即为式(20) 中的Pykyk,样本均值为0.当已知故障发生概率α时,设
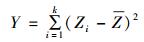
|
(36) |
门限值为m,且关于Y值大于m的概率为α有P(Y>m)=α,则
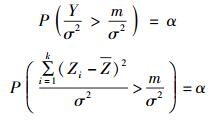
|
(37) |
根据式(35) 可知,此时大于号左边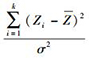
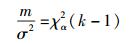
|
(38) |
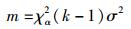
|
(39) |
即门限值m大小为
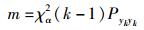
|
(40) |
m确定后定义用于校正状态估计的函数
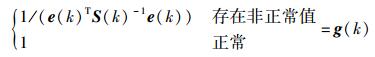
|
(41) |
进而修正状态估计为
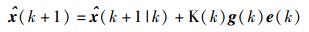
|
(42) |
仿真采用圆形运动的机动方式.在第0~60 s之间,对模型噪声方差的变动做出如下假设
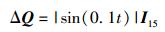
|
(43) |
观测干扰函数为
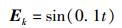
|
(44) |
在上述假定情况下,平台失准角估计误差在卡尔曼滤波、扩展卡尔曼滤波、UKF和双重自适应UKF 4种滤波方法下的估值结果如下.
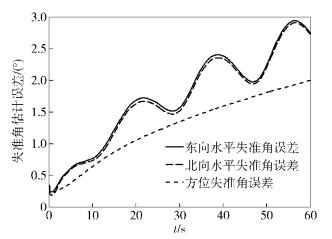
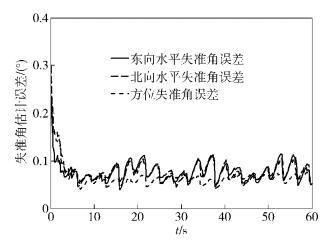
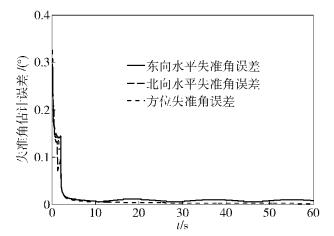
由图 2~5可以看出,应用传统卡尔曼滤波,在仿真时间内失准角误差不能收敛,且误差随时间增大.应用扩展卡尔曼滤波,失准角误差有收敛趋势,但收敛后,误差仍较大且波动剧烈.对准时间为5 s左右,误差范围为0.05~0.2°.应用UKF,随滤波进行,失准角误差快速减小,并明显收敛,但仍有小范围波动.对准时间为3 s左右,误差范围为0.05~0.1°.应用双重自适应UKF,失准角误差快速收敛并接近于零,且稳定在0.01°左右无明显波动,对准时间提高至2 s左右.提出的双重自适应UKF算法对模型噪声和观测干扰有很好的滤波效果,既能适应模型噪声的变化,又能对观测干扰进行有效抑制,使失准角误差大幅度减小且接近于0,同时使其快速收敛,在对准时间上有微弱改善,并且该算法具有较好的鲁棒性.
|
图 2 卡尔曼滤波失准角估计误差 |
|
图 4 UKF失准角估计误差 |
|
图 5 双重自适应UKF失准角估计误差 |
对UKF算法的2个方面进行了改进,通过对预测值方差变化的监测和判断,增加了可以自适应缩放的因子,使双重UKF算法可以既能适应模型噪声的变化,又能对观测干扰进行有效抑制,增强了滤波的鲁棒性,获得了更为准确和稳定的估值.
| [1] | Abbas T, Zhang Yunyan, Liu Yanjun. SINS initial alignment for small tilt and large azimuth misalignment angles[C]//Communication Software and Networks, 2011 IEEE 3rd International Conference on Digital Object Identifier. Xi'an: IEEE Press, 2011: 628-632. |
| [2] | Mao Yuliang, Chen Jiabin, Song Chunlei, et al. Scaled UKF with reduced sigma points for initial alignment of SINS[C]//The 30th Chinese Control Conference (CCC2011). Yantai: IEEE Press, 2011: 106-110. |
| [3] | 袁信, 俞济祥, 陈哲. 导航系统[M]. 北京: 航空工业出版社, 1993. |
| [4] | Julier S, Uhlmann J. A new extension of the Kalman filter to nonlinear system[C]//SPIE-The International Society for Optical Engineering. Orlando, USA: Society of Photo-Optical Instrumentation Engineers, 1997: 182-193. |
| [5] | Ding Weidong, Wang Jinling, Rizos C. Improving adaptive Kalman estimation in GPS/INS integration[J]. Journal of Navigation, 2007, 60(3): 517–529. doi: 10.1017/S0373463307004316 |
| [6] |
胡迪, 董云峰. 基于自适应UKF的敏感器故障诊断算法[J]. 北京航空航天大学学报, 2011, 37(6): 640–643.
Hu Di, Dong Yunfeng. Sensor fault diagnosis algorithm based on adaptive UKF[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(6): 640–643. |


