2. 北京石油化工学院 信息工程学院, 北京 102600
为提高协作频谱感知的检测精度,提出了一种基于协作感知网络来选择感知用户和估计信噪比的算法. 算法利用感知用户之间采样信号的相关特性,构造了相关矩阵,根据矩阵元素的性质估算出各感知用户的信道特性参数:感知用户信道增益比、信噪比和噪声方差等. 算法的实现仅仅基于感知用户的采样信号,无需借助于主用户的任何先验信息,因而具有极高的实用价值. 同时简要分析了要实现该算法,感知用户数量必须大于等于3. 通过仿真实验验证了不同条件下信噪比和信道增益比的估计效果.
2. Information Engineering College, Beijing Institute of Petrochemical Technology, Beijing 102600, China
An algorithm was proposed, which can choose secondary users and estimate signal to noise ratio (SNR) in order to improve the accuracy of cooperative spectrum sensing. The algorithm constructs a correlation matrix by means of the related characteristics of the signals of secondary users. According to the properties of matrix elements, some parameters of channels, e.g. ratio of channels gain, SNR and variance of noise were estimated. The realization of the algorithm was only based on the sampled signals of secondary users without any prior knowledge of primary users. The number of secondary users must be greater than three in cooperative spectrum sensing network. Simulations testify the effects of the algorithm about SNR and the ratio of channel gain.
认知无线电是Mitola[1]在2000年提出的一种频谱管理方案,该方案的主要思想是当主用户(PU, primary user)空闲时,感知用户(SU, secondary user)临时占用该频段,因而认知无线电能极大地提高频谱的使用效率. 频谱感知是认知无线电的核心和基础,包含两大类:本地检测和协作检测. 由于本地检测无法克服多径衰落、隐藏终端等问题,存在自身固有的局限性,尤其是SU在PU覆盖范围以外的情况,导致其检测性能较差,因此协作频谱检测技术被提出. 协作检测主要是对分布在认知网络内的本地SU数据或结论进行数据融合,利用融合准则给出最后的判决,因此融合准则和本地感知精度对最终判决起重要作用. 笔者提出一种利用信道增益比选择SU和估计SNR的算法,通过对信道增益比的计算达到选择SU的目的,通过对SNR的估计来提高本地感知精度.
一些本地频谱检测算法(匹配滤波器检测、能量检测[2]、循环平稳特征检测[3-4]、统计协方差绝对值检测[5]、特征值检测[6]、自相关检测[7]等)的实现需要信道增益、SNR和噪声功率等信道特性参数,因此信道参数估计在频谱感知中显得尤为重要. 现有估计算法有maximum-likelihood estimator (ML), squared signal-to-noise variance (SNV) estimator, second-and fourth-order moments estimator(M2M4)[8]等, 一种改进型M2M4算法也被提出[9]. 笔者提出了一种利用不同SU采样信号之间的相关特性,构造相关特性矩阵,通过分析和比较相关矩阵对角元素和非对角元素的特性,估算出SU信道增益比和信道特性的算法. 为便于后续的说明,该算法称为互相关矩阵估计(CCM, cross-correlation matrix estimator)算法.
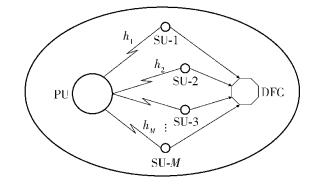
1 系统模型在认知网络区域内,协作感知模型如图 1所示. 其中,SU-i为第i个SU,DFC(data fusion center)为该区域内感知网络的数据融合中心,hi为第i个SU与PU之间的信道增益,M为感知用户数. 不妨设PU载波频率为fc、带宽为B,SU是同步接收PU信号的.
|
图 1 协作感知模型示意图 |
频谱感知可等价为二元假设:① H0,假设PU不存在;②H1,假设PU存在. 即

|
(1) |
其中:xi(t)为第i个SU的接收信号;s(t)为PU发射信号,有E[s(t)]=0,E[s2(t)]=δ2s;ni(t)为第i个SU所叠加的零均值高斯分布白噪声,var [n2i(t)]=δ2ni,则
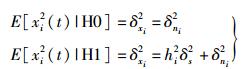
|
(2) |
在nTs时刻对xi(t)信号采样后,二元假设模型为
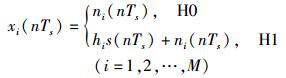
|
(3) |
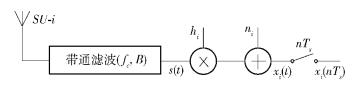
其中Ts为采样周期且能保证接收信号无失真,如图 2所示.
|
图 2 SU信号采样示意图 |
设信号长度为N,为描述的方便,忽略采样周期,用如下向量表示:
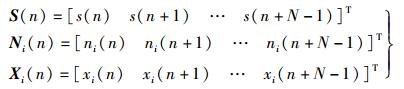
|
(4) |
定义感知信号互相关矩阵为

|
(5) |
易知R为对称方阵,且元素rij描述了感知信号间的相关性. 若rij越大,感知信号间的相关性就越大,PU存在的概率就越大;若rij=0,感知信号间就无相关性,也就说明感知信号为白噪声的概率较大,即PU不存在.
2 理论分析矩阵R的对角元素为SU采集到的发射信号功率叠加噪声方差,由于不能确定PU是否存在以及信道的噪声方差,矩阵R的对角元素并不能反映出信道的任何特性. 为此,将R的元素分为对角元素和非对角元素两类来进行分析.
2.1 矩阵元素特性分析在矩阵R中任取元素rij,因为ni、nj均为高斯分布的白噪声,且N足够大,则
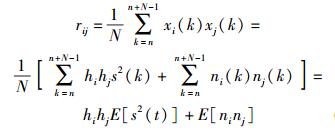
|
(6) |
1) 当i≠j时,非对角元素只与信道增益和信号功率有关,而与加性噪声无关. 若PU存在,则rij(i≠j)=hihjδ2s;若PU不存在,则rij(i≠j)=0.
2) 当i=j时,rij为矩阵的对角元素,实为信号功率与噪声方差叠加. 若PU存在,则rii=h2iδ2s+δ2ni;若PU不存在,则rii=δ2ni.
2.2 信道增益比在感知网络中任取3个不同的SU(i,j,k),其对应的信道增益不妨设为hi、hj和hk,有rik=hihkδ2s,rjk=hjhkδ2s,令信道增益比为
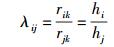
|
(7) |
当λij>1时,i对应的信道增益要大于j对应的信道增益;当λij﹤1时,j对应的信道要大于i对应的信道增益;当λij=1时,两信道增益一样. 可以据此比较出各个SU接收到PU发射信号的衰减度. 为提高λij的精度,亦可利用式(8)求其平均值后再进行比较.
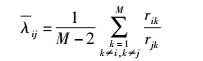
|
(8) |
由2.1节的分析,有

|
(9) |
其中pi为第i个感知用户接收信号SNR,则
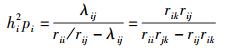
|
(10) |
易证该SNR估计是无偏的(见附录).
信道噪声方差为
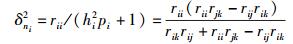
|
(11) |
SU接收到的PU信号功率为
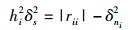
|
(12) |
利用式(8)亦可求SNR、噪声方差和PU信号功率的平均值来提高估计量的精度.
以上分析均假设PU存在. 当PU不存在时,rij(i≠j)=0,R为一对角阵,此时以上公式将不再适用,但可直接给出PU空闲的判决. 而实际情况是理想白噪声是不存在的,N也不是取无穷大,并且感知信号的精度也是有限的,因此即使PU不存在,也不会出现非对角元素为零的情况,而是一个趋于零的极小量,CCM仍然有效.
算法是从感知网络中任取3个不同的SU实现的,这就要求该算法的实现必须要保证协作频谱的SU数必须大于或等于3,即M≥3.
3 CCM算法的实现认知网络内SU数为M,采样信号长度为N,则感知信号可表示为
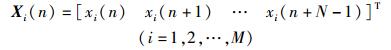
|
(13) |
算法实现步骤如下:
1) 将式(13)代入式(5)构造互相关矩阵R;
2) 将矩阵元素代入式(8),可求出各SU平均信道增益比较因子
3) 由式(10)~式(12)可分别计算出各SU接收信号的SNR、噪声方差和信号功率.
上述算法的实现过程只与相关矩阵R的元素有关,无需PU的任何先验信息,因而算法的实现极为简单.
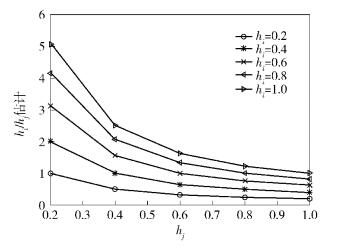
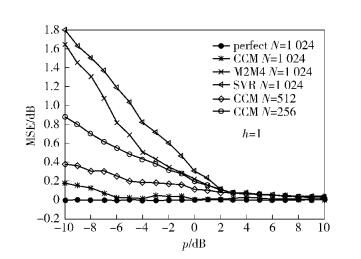
4 仿真为评价CCM算法的效果,图 3显示了不同信道衰减下的h2SNR估计值与SNR实际值之间的比较,显然当信道无衰减时,估计值与实际值之间几乎没有偏差,随着信道衰减加剧,SNR的估计值与实际值之间的偏差越来越大,因此选择信道衰减小的SU参与数据融合有利于提高检测精度. 图 4显示了不同信道衰减下λij的估计值,对同一个hj,若hi/hj越小,则第i个SU信号衰减的就越严重. 因此在数据融合时,可以依据λij的大小,对不同信道衰减程度的SU给予不同权重的关注. 由于认知无线电中,SU无PU的先验信息,为便于各算法性能的比较,假定信道无衰减,本节仿真了CCM算法与其他算法(M2M4算法、SVR算法). 设PU发射信号为经滚降系数为0.5的均方根余弦函数成型后的QPSK调制信号,载波频率fc=20 MHz,B=1 kHz,fs=32 kHz,M=5. 图 5所示为SNR估计值与真实值的均方误差(MSE),用Δ表示,定义为
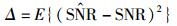
|
(14) |

|
图 3 不同信道衰减下的h2p估计值 |
|
图 4 信道增益比λij估计值 |
|
图 5 SNR估计MSE |
其中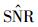
协作检测能大大提高频谱感知的性能,但本地检测结论必须准确可靠,因而估算更多的本地检测的环境参数,如信道增益、SNR、噪声方差等极为必要. 为此提出了构造SU相关矩阵,仅仅基于矩阵元素估算出信道增益比、SNR等的算法. 通过信道增益比的估计能选择性能更加可靠的SU,通过SNR的估计能提高本地检测精度. 算法的实现无需PU和信道的任何先验信息,只需对不同SU接收的信号进行互相关运算即可,并给出了计算SNR、噪声方差的显示表达式,因而计算简单,实用性极强.
附录证明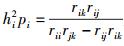
证明:因为
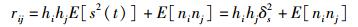
|
有

|
当信道无衰减,即hi=1时
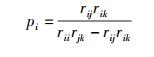
|
证毕.
| [1] | Mitola J. Cognitive radio: an integrated agent architecture for software defined radio [D]. Sweden: Royal Institute of Technology, 2000. http://www.scirp.org/reference/ReferencesPapers.aspx?ReferenceID=1062382 |
| [2] | Harry Urkowitz. Energydetection of unknown deterministic signals[J]. Proc of the IEEE, 1967, 55(4): 523–531. doi: 10.1109/PROC.1967.5573 |
| [3] | Dandawate A V, Giannakis G B. Statistical tests for presence of cyclostationarity[J]. IEEE Transaction on Signal Processing, 1994, 42(9): 2355–2369. doi: 10.1109/78.317857 |
| [4] |
虞贵财, 罗涛, 黄振, 等. 感知无线电系统中改进的循环频谱检测算法[J]. 北京邮电大学学报, 2009, 32(2): 89–92.
Yu Guicai, Luo Tao, Huang Zhen, et al. An improved cyclic spectrum detection algorithm in CR systems[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(2): 89–92. |
| [5] | Zeng Yonghong, Liang Yingchang. Spectrum-sensing algorithms for cognitive radio based on statistical covariances[J]. IEEE Transaction on Vehicular Technology, 2009, 58(4): 1804–1815. doi: 10.1109/TVT.2008.2005267 |
| [6] | Zeng Yonghong, Liang Yingchang. Maximum-minimum eigenvalue detection for cognitive radio[J]. IEEE Transactions on Communications, 2009, 57(6): 1784–1093. doi: 10.1109/TCOMM.2009.06.070402 |
| [7] | Mort Naraghi-Pour, Takeshi Ikuma. Autocorrelation-based spectrum sensing for cognitive radios[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 718–733. doi: 10.1109/TVT.2009.2035628 |
| [8] | David R, Pauluzzi, Norman C. Beaulieu. A comparison of SNR estimation techniques for the AWGN channel[J]. IEEE Transactions on Communications, 2000, 48(10): 1681–1691. doi: 10.1109/26.871393 |
| [9] | Ren Guangliang, Chang Yilin, Zhang Hui. A new SNR’s estimator for QPSK modulations in an AWGN channel[J]. IEEE Transactions on Circuits and Systems-Ⅱ: Express Briefs, 2005, 52(6): 336–338. doi: 10.1109/TCSII.2005.849008 |


