提出了一种优化认知双向中继系统生存时间的中继节点选择策略.基于解码转发型协议, 次级用户作为主用户系统的中继节点对接收信号进行处理, 在帮助主用户系统进行数据传输的同时, 可实现次级用户系统的数据传输.通过引入每次数据传输所需的发射功率、中继节点剩余能量以及系统中断概率等因素, 能有效地提高系统长期吞吐量, 延长系统生存时间.
A relay node selection strategy was proposed to improve the long-term throughput and extend the lifetime of system. Based on decode-and-forward relay protocol, the secondary user was pretended as a relay node of the primary system to assist the primary user pair to communicate. Meanwhile, data transmission for the secondary system was achieved. The proposed strategy introduces three factors, i.e. the transmit power required for each data transmission, the remaining energy of relay nodes as well as the probability of system outage. Therefore, the long-term throughput can be improved and the lifetime of system can be extended effectively.
中继技术被认为是一种可有效提升通信系统鲁棒性的新型技术[1],近来,一种认知双向中继系统得到了学术界的关注[2].在限制对主用户一定干扰约束下,Li等[3]提出了一种联合中继选择和资源分配的优化策略来最大化系统吞吐量,但仅仅考虑了一次数据传输的中继选择策略,忽略了如何延长无线中继认知系统的生存时间.
系统生存时间定义为系统发生中断前,系统能进行数据信息传递的最大次数[5].在无线认知双向中继系统中,基于解码转发型 (DF) 中继协议提出了一种最优中继选择策略. 2个主用户通过1个次级用户的帮助进行通信.次级用户可作为中继获得频谱共用的机会,并采用解码转发双向中继协议对主用户的信号进行处理.通过进行中继节点选择来提升系统长期吞吐量,延长系统生存时间.
1 双向中继认知系统模型如图 1所示,在无线双向中继认知系统中,包含1个主用户对 (PU pair) 和K个次级用户对 (SU pairs),并采用3阶段双向中继协议,在中继节点处对信号的处理采用解码转发策略.假设主用户对A和B节点间遭受严重的阴影衰落,导致A和B之间没有直传链路.

|
图 1 无线双向认知中继系统模型 |
主用户对A和B通过1个次级用户源节点Sk进行通信,其中k∈{1, 2, …, K}.而次级用户源节点Sk的任务是作为主用户系统的中继节点r,来得到频谱共享的机会.在此,次级用户系统信号是由假装为中继节点r的次级用户源节点发送给其对应的次级用户目的节点d,d∈{D1, D2, …, DK},其中Dk表示第k个次级用户用户目的节点,下面介绍3阶段双向解码转发中继认知系统的信息传递处理过程:
第1阶段 主用户A广播它的信息xA,发射功率为PA,则在次级用户源节点Sk和次级用户目的节点Dk处,接收信号可以分别表示为
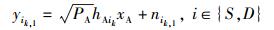
|
(1) |
其中:hASk和hADk是从主用户A到次级用户源节点Sk和次级用户目的节点Dk的信道系数,并且,hAkS~CN (0, σAS2),hADk~CN (0, σAD2),其中,信道均为瑞利衰落信道. nSk, 1和nDk, 1分别是在次级用户对Sk和Dk处的加性白高斯噪声.为了简化,假设噪声均为加性零均值白高斯变量,方差为σn2.
第2阶段 主用户B广播它的信息xB,发射功率为PB.则在次级用户源节点Sk和次级用户目的节点Dk处,接收信号可以分别表示为

|
(2) |
其中,hBSk和hBDk是从主用户B到次级用户源节点Sk和次级用户目的节点Dk的信道系数,并且,hBSk~CN (0, σBS2),hBDk~CN (0, σBD2). nSk, 2和nDk, 2分别是在第2个阶段,次级用户Sk和Dk处的加性白高斯噪声.
第3阶段 从次级用户源节点集合中选择1个次级用户源节点,作为主用户系统中继节点,即r∈{S1, S2, …, SK}.上述次级用户信号是发送给其对应的次级用户目的节点d, d∈{D1, D2, …, DK}.假设主用户信号xA和xB在中继节点r处都能被正确解码,由于采用解码放大转发 (DF) 中继协议,故在中继节点处,生成1个基于网络编码的主用户合成信号
被选中的中继节点r又重新生成了1个复合信号xr,这个信号xr是将主用户合成信号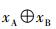
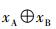
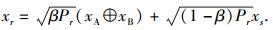
被选中的中继节点r广播复合信号xr,则在主用户A、B和次级用户目的节点d处,接收信号可以分别表示为

|
(3) |
在通过完美的自解码过程后,在主用户A和B处的接收信号转化为

|
(4) |
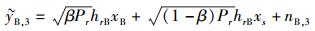
|
(5) |
在经过完美的干扰消除后,在次级用户目的节点处的接收信号可以表示为

|
(6) |
因此,在主用户节点A、B以及次级用户目的节点d处的瞬时信噪比可以分别表示为
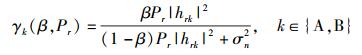
|
(7) |
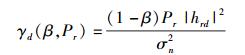
|
(8) |
故在主用户节点A、B以及次级用户目的节点d处的瞬时信道可达速率可以分别表示为

|
(9) |
要保证系统不发生中断,要求瞬时可达速率满足实际速率需求,假设主用户A、B、次级用户源节点 (中继)r的实际速率需求分别是RA,RB,Rr,必须保证CAA≥RB, CBB≥RA, Cdd≥Rr.为简化,假设Rth=RA=RB=Rr,并且定义γth=23Rth-1,则将对于信道速率要求的约束可以转化为
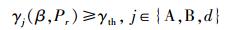
|
(10) |
令er[m]标记中继节点r在第m个时隙开始时的剩余能量,假设每次传输持续1个时隙,并且发射功率等于本次传输时间内的能量消耗.中继节点r在第m次传输时的最大发射功率表示为Pr, max[m]=max{εi:εi≤er[m], i=1, 2,…, L}.并且,每个中继节点都有一个最大发射功率约束Pmax和L个离散功率等级,可以表示为
当主用户A、B和对应次级用户目的节点的瞬时SNR均低于目标值γth时,中继r服务的链路就发生中断,即在第m个时隙,中继节点r的中断概率可以表示为

|
(11) |
在此,Zr=|hAr|2的概率密度函数可以表示为

|
(12) |
其中r=1, 2, …, K.类似地,可以得到Zr=|hBr|2或Zr=|hrd|2.
因此,主用户A的瞬时SNR值满足目标值γth时的概率可以推导如下:

|
(13) |
可令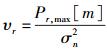

|
(14) |
类似地,主用户B的瞬时SNR值满足目标值γth时的概率,表示如下:

|
(15) |
对于对应次级用户目的节点d,其接收信号SNR满足目标值的概率,可以推导如下:

|
(16) |
则中继节点r的中断概率可以表示为

|
(17) |
其中
令E[m]=[e1[m], e2[m], …, eK[m]],令E[1]表示所有中继节点的初始能量分布, 在1个时隙中只有1个中继节点能被选中来协助数据传输.对于任何合理的中继选择策略,不论中继的信道状况如何,只有当它的剩余能量能实现目标SNR值时,它才能够被选中进行协作传输.
因此,当且仅当没有中继能够满足目标SNR值,则认为系统发生中断.给定第m个时隙开始时的剩余能量值是E[m],则整个无线双向中继认知系统的中断概率可以表示为

|
(18) |
系统生存时间可以定义为
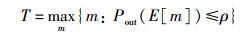
|
(19) |
其中门限ρ是系统最大容忍中断概率.即系统生存时间被定义为:系统中断概率不大于ρ时,系统能达到的最大传输次数m.因此,平均系统网络生存时间可以表示为

|
(20) |
其中:er[1]是中继节点r的初始能量,ξw是平均浪费能量即当系统生存时间到达时所有中继节点剩余能量之和,ξt是每次传输平均消耗的能量.
2 中继节点选择策略由于每个中继节点处均有最大功率限制Pmax,1个中继节点被选中,必须满足
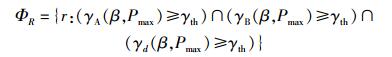
|
其中:ΦR表示满足主用户发送接收端以及次级用户目的节点SNR均大于门限值的中继节点集合.如果所有的中继节点在同一时刻都遭受深度衰落以致于ΦR变为空集,发生中断.但是只要系统的中断概率仍然低于给定门限ρ,则系统仍然被认为处于存活态.
令Γr是中继r实现目标SNR的所需最小发射功率级,即对于r∈ΦR,可以得到

|
中继节点处的功率限制:

|
上述3个式子要保证Pr≥0,则β需满足

|
(21) |
且根据中断概率表达式,只有当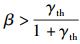
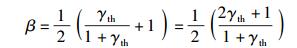
|
(22) |
将此式代入中继节点功率限制条件中,可以得到 (η1, η2, η3) 的更新表达式为

|
因此,在满足系统速率需求时,中继节点所需最小发射功率为
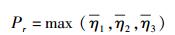
|
(23) |
由于功率取值为离散化值,故中继所需复合离散级别的发射功率为

|
(24) |
为了最大化系统生存时间,中继选择必须最小化平均的能量消耗以及浪费的能量.由于空间分集作用,最小平均发射功率与中继节点的个数成反比,因此,需要保证激活的中继节点数目来降低能量消耗的速度.
根据上述分析,基于局部瞬时信道信息CSI和剩余能量REI,即Γr[m]和er[m], 提出了一个基于效用函数Ur的中继节点选择策略.为了选择一个合适的中继节点,Ur必须满足以下约束条件.
1) 对于第m次传输,中继节点r更可能被选中:当它的剩余能量er[m]大于其他中继节点的剩余能量.因此Ur是本次中继剩余能量er[m]的单调递增函数.
2) 对于第m次传输,中继节点r不大可能被选中:如果它本次所需的发射功率大于其他中继节点.因此,Ur是本次发射功率Γr[m]的单调递减函数.
3) 对于第m次传输,中继节点r比较可能被选中:如果它能在本次信息传输后,实现系统中断概率最小化.
由于所有中继节点都是公平地被选择,所以当中继节点的剩余能量较多或者其本次发射功率较小时,这个中继节点有更多的机率会被选中.为了满足上述需求,提出了一种灵活的效用函数:
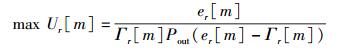
|
(25) |
在所提中继选择策略中,效用函数Ur既是本次中继剩余能量er[m]的单调递增函数,也是本次发射功率Γr[m]的单调递减函数,同时考虑到在本次信息传输后,实现系统中断概率最小化.
3 仿真结果分析仿真结果证明了所提的中继节点选择策略优于现有文献中的3种中继选择策略[4-5],即最小发射功率策略、最大化剩余能量策略、最小化系统中断概率.仿真参数设置中,作为中继节点的次级用户源节点取值为5,每个中继节点的初始能量均相同,能量变化范围是250~500 J;系统中断概率门限取值为0.1;功率等级L取值为10.
图 2给出了系统生存时间随中继节点初始能量的变化趋势.从仿真结果中可以观察到,所提中继选择策略能够实现系统生存时间的最大化.最大化剩余能量中继选择策略实现的系统性能优于最小化系统中断概率中继选择策略,而最小化发射功率中继选择策略又优于最大化剩余能量中继选择策略.这是因为最小化发射功率能节省每次传输所需的发射功率却容易导致系统中的某些中继节点提前失活,导致系统中断概率增大;而最大化剩余能量中继策略不能保证每次传输所需的发射功率最小,但是却能对系统中继节点的激活程度进行均衡,不会导致某些中继节点提前失活;最小化系统中断概率策略不能保证每次传输所需的发射功率最小,还由于保证系统中断概率的约束,导致本次传输所消耗的发射功率值增大.然而,所提中继节点选择策略,充分考虑到中继节点发射功率、剩余能量和系统中断概率的问题,因此相对于上述3种中继选择策略来说,实现的系统生存时间是最优的.

|
图 2 系统生存时间与中继初始能量的比较 |
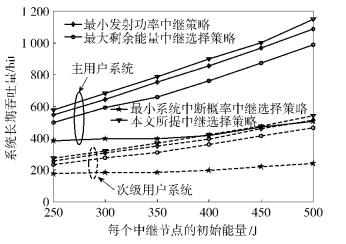
图 3给出了主用户/次级用户系统长期吞吐量随中继节点初始能量的变化趋势.系统长期吞吐量是指在系统生存时间段内的吞吐量总和.从仿真结果中可观察到所提策略能够实现系统生存时间的最大化.
|
图 3 主/次级用户系统长期吞吐量与中继初始能量的比较 |
图 4给出了中继节点平均浪费能量与中继节点初始能量的变化情况.从仿真结果看出,所提中继节点选择策略的能量浪费最少,最小化系统中断概率选择策略的能量浪费最多.这是因为最小化系统中断概率选择策略需要在每次进行中继选择后,保证系统中断概率最小化,这会导致某些剩余能量较小的次用户本可被选中,但为使每次中继选择后保证系统中断概率最小,这些次用户有可能就一直不能被选中,直到系统中断概率超过一定门限时,系统即被认定失活,而上述次级用户即使还具有能量能进行中继传输,但是由于已认定系统失活,则这些次用户的剩余能量也就浪费了.而所提中继节点选择策略,考虑到中继节点发射功率、剩余能量和系统中断概率等方面,因此,相对于上述3种策略来说,能充分利用系统能量,实现系统生存时间最优并且浪费能量最少.

|
图 4 中继平均浪费能量与中继初始能量的比较 |
在认知双向中继系统下,提出了一种优化的中继节点选择策略,以提高系统长期吞吐量和延长系统生存时间.在无线认知双向中继系统中,次级用户可作为主用户系统中的中继节点,采用DF协议来对接收信号进行处理,在帮助主用户系统进行数据传输的同时,也实现次级用户系统的数据传输.所提优化中继选择策略,充分考虑每次数据传输所需的发射功率、中继节点剩余能量以及系统中断概率等因素,仿真结果证明所提优化中继选择策略能够有效地提高系统长期吞吐量、延长系统生存时间.
| [1] | Sydir J, Taori R. An evolved cellular system architecture incorporating relay stations[J]. IEEE Communications Magazine, 2009, 47: 115–121. doi: 10.1109/MCOM.2009.5116808 |
| [2] | Li Qiang, Ting S H, Pandharipande A. Cognitive spectrum sharing with two-way relaying systems[J]. IEEE Transactions on Vehicular Technology, 2011, 60: 1233–1240. doi: 10.1109/TVT.2010.2104334 |
| [3] | Li Liying, Zhou Xiangwei, Xu Hongbing. Simplified relay selection and power allocation in cooperative cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 10: 33–36. doi: 10.1109/TWC.2010.101810.100311 |
| [4] | Hui Hui, Zhu Shihua, Lü Gangming. Relay selection for lifetime extension in amplify-and-forward cooperative networks[C]//Communications (ICC), 2010 IEEE International Conference on. Cape Town, South Africa: IEEE, 2010: 1-5. |
| [5] | Huangwanan Jen, Hongyao Win, Kuo C-C. Lifetime maximization for amplify-and-forward cooperative networks[J]. IEEE Transactions on Wireless Communications, 2008, 7: 814–818. |


