基于证书的密码体制结合了基于公钥基础设施的密码体制和基于身份的密码体制的优点,既简化了公钥的管理又不存在密钥托管问题,对一个无双线性对的基于证书的签名方案进行了密码学分析,指出该方案存在类型II攻击者的伪造性攻击和其证明中的不当之处,并用散列函数绑定随机数的方法对其进行了改进. 改进方案在离散对数是困难问题的假设下,在最强的安全模型中被证明是安全的. 由于不需要耗时的双线性对运算,新方案效率较高,适合于无线传感器网络等能量受限的系统使用.
Certificate-based cryptosystem combines the merits of public key infrastructure (PKI)-based cryptosystem and identity-based cryptosystem, which can not only simplify the public key management, but also avoid the key escrow problem. A certificate-based signature scheme without pairing is analyzed, and shown to be forgeable by a type II attacker. In the proof, there exists a security flaw, which is improved by means of binding random number to hash function. The improved scheme is proven to be unforgeable in the strongest security model of certificate-based signature scheme under discrete logarithm assumption. Without any time-consuming bilinear pairing operations, it shows efficient and applicable to power-constrained devices, such as wireless sensor networks.
基于公钥基础设施(PKI,public key infrastructure)的密码体制需要一个可信第3方认证中心(CA,certificate authority)签发一个证书来把用户的公钥和其身份进行绑定,这种体制的主要缺点是公钥管理费用高. 基于身份的密码体制[1]可以大大简化公钥的管理,但基于身份的密码体制存在密钥托管问题.
为解决基于PKI的密码体制需要高昂的公钥管理费用问题和基于身份密码体制存在的密钥托管问题,Gentry[2]于2003年提出了基于证书的密码体制. 基于证书的密码体制采用隐式认证的方法来验证用户证书的合法性. 隐式认证省去了第3方询问证书状态的需求,从而降低了公钥管理的成本,并且基于证书的密码体制也不存在密钥托管问题;另外,基于证书密码体制中的证书虽然是作为部分私钥使用,却不需要保密,因而可以克服基于身份密码体制中需要安全信道来传送私钥的问题.
2004年Kang等[3]将基于证书的密码体制推广到签名,首次提出一个基于证书的签名方案. 2007年,Li等[4]指出文献[3]方案存在公钥替换攻击,并重新定义了基于证书的签名的安全模型. 2008年,Wu等[5]对基于证书的签名的安全模型进行总结,提出了一般攻击者模型、强攻击者模型和超级攻击者模型.
2012年,杨等[6]提出一个基于证书的签名方案,方案不需要耗时的双线性对运算,效率较高,在文献[5]中的最强安全模型下给出了方案的安全性证明. 然而,笔者指出文献[6]的方案是不安全的,一个类型II攻击者可以任意伪造用户的签名,并指出他们证明过程中的不当之处,进而提出一个改进方案,改进方案在文献[5]的最强的安全模型下可证明是安全的.
1 基本概念 1.1 离散对数问题(DLP, Discrete Logarithm Problem)设p和q是2个大的素数,满足q|p-1,g是非零模p剩余类Zp*中阶为q的生成元. 离散对数问题是,给定一个实例(y,p,q,g),其中y=gxmod p,x∈Zq*,要求计算x.
1.2 离散对数假设一个概率多项式时间算法B被称为(t,ε)攻破DLP的一个实例(y,p,q,g),其中y=gxmod p,x∈Zq*,假如B能以ε概率,运行最多t步计算出x.
定义1 离散对数假设. 不存在任何多项式时间攻击者,能(t,ε)攻破离散对数问题.
1.3 基于证书的签名的形式化定义一个基于证书的签名方案由以下5个算法组成.
1) 初始化(setup). 输入安全参数k,算法输出系统主私钥s、主公钥Ppub和系统公开参数Pparam.
2) 用户密钥产生(UserKeyGen). 输入系统公开参数Pparam和用户身份ID,算法输出用户的私钥和公钥对(xID,yID).
3) 证书产生(CertGen). 输入系统公开参数Pparam、主私钥s、用户身份ID、用户公钥yID和时段参数j,算法输出用户该时段的证书 CertID, j.
4) 签名算法(sign). 输入系统公开参数Pparam、用户密钥对(xID,yID)、用户证书CertID, j、消息m,算法输出一个签名σ.
5) 验证算法(verify). 输入系统公开参数Pparam、消息m、签名σ、用户的公钥yID,算法输出1或0. 如果输出是1表示签名正确,否则表示签名不正确.
以上算法要求σ=Sign(xID,CertID,j,m),概率Pr [Verify(m,yID,σ)=accept]=1.
1.4 基于证书的签名的安全模型在基于证书的签名的安全性要求中,某个身份为ID的用户,他必须同时拥有证书CertID, j和私钥xID才能产生正确的签名,缺少其中任何一个都不行.
在基于证书的密码体制中,存在两类攻击者[2]. 第1类攻击者AⅠ不知道系统主私钥,模拟的是一般用户的攻击,它能替换任意用户的公钥;第2类攻击者AⅡ知道系统主私钥,它可以产生任意用户的证书,但不知道用户私钥,它不能替换挑战用户的公钥. 基于证书的签名方案在第1类攻击者AⅠ和第2类攻击者AⅡ下,都需要满足不可伪造性.
定义2 类型Ⅰ攻击下的不可伪造性.
在适应性选择消息和适应性选择身份攻击下,如果不存在任何多项式有界的攻击者AⅠ,能以不可忽略的概率赢得以下游戏,则称一个基于证书的签名方案是在类型Ⅰ攻击下超级攻击者安全的.
1)初始化. 输入安全参数k,挑战者C运行setup,输出系统主私钥s、主公钥Ppub和系统公开参数Pparam. C返回Ppub和Pparam给AⅠ,保密主私钥s.
2)阶段1. 攻击者适应性地进行多项式有界次的以下询问:
a)用户生成询问. 攻击者选择用户身份ID,如果该ID的密钥对还未产生,C运行UserKeyGen算法产生该用户的私/公钥对(xID,yID),并返回yID给攻击者;否则直接返回yID给攻击者.
b)私钥询问. 攻击者选择一个已经生成的用户身份ID,C返回该用户原始公钥对应的私钥xID给攻击者.
c)替换公钥询问. 在任何时候,AⅠ选择一个新的公钥y′ID替换原来的公钥yID,并且攻击者不用提供相应的私钥.
d)证书询问. 攻击者选择用户ID和公钥yID,C运行CertGen算法产生该用户在时段j的证书CertID, j,并返回给攻击者. 攻击者不用提供对应公钥yID的相应的私钥.
e)超级签名询问. 攻击者选择用户ID和消息m,C使用用户当前的公钥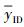

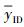
3)伪造. 攻击者输出一个用户ID′的伪造的签名(m′,σ′). 设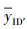
a)Verify(m′,σ′,
b)攻击者没有对(m′,ID′)作超级签名预言机询问;
c)攻击者没有对(ID′,
攻击者的优势定义为他在以上游戏中获胜的概率.
定义3 类型Ⅱ攻击下的不可伪造性.
在适应性选择消息和适应性选择身份攻击下,如果不存在任何多项式有界的攻击者AⅡ能以不可忽略的概率赢得以下游戏,则称一个基于证书的签名方案是在类型Ⅱ攻击下超级攻击者安全的.
1)初始化. 输入安全参数k,挑战者C运行setup,输出系统主私钥s、主公钥Ppub和系统公开参数Pparam. C返回Ppub、Params和s给AⅡ.
2)阶段1. 攻击者适应性地进行多项式有界次的以下询问:
a)用户生成询问;b)私钥询问;c)替换公钥询问;d)超级签名询问. 这些询问同定义2.
3)伪造. 攻击者输出一个用户ID′的伪造的签名(m′,σ′). 设yID′是用户ID′的原始公钥. 假如满足以下条件,则攻击者赢得游戏.
a)Verify(m′,σ′,yID′)=1;
b)攻击者没有对(m′,ID′)作超级签名预言机询问;
c)攻击者没有对ID′的私钥进行查询.
攻击者的优势定义为他在以上游戏中获胜的概率.
2 杨波等人的方案 2.1 具体方案setup:输入安全参数k,CA产生2个大的素数p和q,q|p-1,随机选取Zp*的一个阶为q的元素g,gq=1(mod p), q≠1. CA随机选取主私钥s∈Zq*,计算主公钥Ppub=gs (mod p),选取3个安全Hash函数H1、H2、H3,它们均将{0,1}*映射到Zq*,公开系统参数{p,q,g,Ppub,H1,H2,H3},保密私钥s.
UserKeyGen:用户ID随机选取xID∈Zq*作为私钥,计算公钥yID=gxID(mod p).
CertGen:给定一个用户身份ID和公钥yID,CA验证用户身份后,如果有效,则随机选择r∈Zq*,计算R=gr(mod p),zID=r+sH1(R,ID,yID). 发送证书CertID=(zID,R)给用户.
sign:输入消息m,用户ID随机选择u∈Zq*,计算U=gu(mod p),v=u+zIDH2(ID,U,yID,m)+xID H3(ID,U,yID,m),消息m的签名σ=(U,v,R).
verify:验证者收到消息m的签名σ=(U,v,R)后,计算V=gv(mod p),a=H1(R,ID,yID),b=H2(ID,U,yID,m),c=H3(ID,U,yID,m),然后验证等式V=U(RPpuba)byIDc是否成立. 成立则验证者接受签名,否则拒绝.
2.2 对以上方案的攻击这里给出一种对原方案的类型Ⅱ攻击者的伪造攻击. 设用户身份为ID,公钥为yID,可信中心CA可对该用户进行任意消息伪造. 对任意消息m,CA任选t,u∈Zq*,计算U=gu(mod p),h1=H1(R,ID,yID),h2=H2(ID,U,yID,m),h3=H2(ID,U,yID,m),R=(gtyID-h3)h2-1,v=u+t+sh1h2,则伪造的签名为σ=(U,v,R). 显然,伪造的签名能通过验证. 因为
在原方案的证明中,定理1用到了多Forking引理[7],定理2用到了通用Forking引理[8],而多Forking引理和通用Forking引理都是由Forking引理[9]发展而来的,实际上它们成立的条件是要求签名方案是一个通用数字签名方案,即给定消息m,它产生一个三元组(σ1,h,σ2),其中:σ1随机地取自一个大的集合,h是(m,σ1)的hash值,σ2仅依赖于σ1、m和h. 而反观原方案,签名是(U,v,R),它并不是一个通用数字签名方案,因为v的计算用到zID从而和R发生关系,而H2(ID,U,yID,m)和H3(ID,U,yID,m)的计算中都没有包含R这一部分,所以通用Forking引理和多Forking引理都不适合使用,所以原方案的证明不正确.
3 一个改进的方案 3.1 具体方案setup、UserKeyGen和 CertGen同原方案.
sign:输入消息m,用户ID随机选择u∈Zq*,计算U=gu(mod p),v=u+zIDH2(ID,U,yID,m,R)+xID H3(ID,U,yID,m,R),消息m的签名σ=(U,v,R).
verify:验证者收到消息m的签名σ=(U,v,R)后,计算V=gv(mod p),a=H1(R,ID,yID),b=H2(ID,U,yID,m,R),c=H3(ID,U,yID,m,R),然后验证等式V=U(RPpuba)byIDc是否成立. 成立则验证者接受签名,否则拒绝.
3.2 改进方案的安全性分析定理1 类型Ⅰ攻击下的不可伪造性. 在随机预言机模型中,在适应性选择消息和适应性选择身份攻击下,如果存在一个攻击者AⅠ能在多项式时间内以ε的优势伪造一个签名,他最多进行qHi(i=1,2,3)次Hash询问,qUC次用户生成询问,qCG次证书生成询问,则存在一个挑战者C,能在多项式时间内以
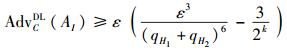
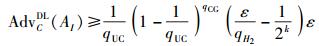
定理2 类型Ⅱ攻击下的不可伪造性. 在随机预言机模型中,在适应性选择消息和适应性选择身份攻击下,如果存在一个攻击者AⅡ能在多项式时间内以ε的优势伪造一个签名,他最多进行qHi (i=1,2,3)次Hash询问,qUC次用户生成询问,qPKR次公钥替换询问,则存在一个挑战者C,能在多项式时间内以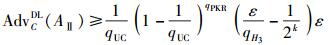
限于篇幅,这里仅给出以上2个定理的证明大意:系统的初始化和随机预言机的询问和应答都与原方案类似,只是在运用多Forking引理和通用Forking引理的条件上与原方案不同. 注意到,改进方案的最后签名也是(U,v,R),与原方案不同的是H2(ID,U,yID,m,R)和H3(ID,U,yID,m,R)的计算包含了R,这样U、R对应于通用数字签名中的σ1,H2和H3对应于h,v对应于σ2,所以,改进方案是一个通用数字签名方案,所以能够运用多Forking引理和通用Forking引理.
4 结束语基于证书的密码体制具有基于PKI的密码体制和基于身份密码体制的优点,同时又克服了它们的缺点. 本研究对一个基于证书的不使用双线性对的签名方案进行了密码学分析,指出一个类型Ⅱ攻击者可以伪造任意消息的签名,进而提出一个改进方案. 改进方案能被证明在文献[5]的最强的安全模型中是安全的. 由于不需要耗时的双线性对运算,方案效率较高,适合于能量受限的系统,如无线传感器网络的使用. 下一步的工作是进一步研究基于证书的具有特殊性质的签名方案,如基于证书的群签名和门限签名等.
| [1] | Shamir A. Identity-based cryptosystems and signature schemes[C]//Edited by Goos G and Hartmanis J. Proc of Crypto’84. Berlin: Springer-Verlag, 1984: 47-53. http://www.academia.edu/2686074/Security_Mediated_Certificateless_Signatures |
| [2] | Gentry C. Certificate-based encryption and the certificate revocation problem[C]//Edited by Goos G, Hartmanis J, and Leeuwen J V. Proc of EuroCrypt’2003. Berlin: Springer-Verlag, 2003: 272-293. https://es.scribd.com/document/330741472/Applied-Cryptography-and-Network-Security-tqw-darksiderg |
| [3] | Kang B G, Park J H, Hahn S G. A certificate-based signature scheme[C]//Edited by Goos G , Hartmanis J, and Leeuwen J V. Proc of CT-RSA’04. Berlin: Springer-Verlag, 2004: 99-111. http://www.buptjournal.cn/CN/abstract/abstract1783.shtml |
| [4] | Li Jiguo, Huang Xinyi, Mu Yi, et al. Certificate-based signature: security model and efficient construction[C]//Edited by Lopez J, Samarati P and Ferrer J L. Proc of EuroPKI’ 07. Berlin: Springer-Verlag, 2007: 110-125. |
| [5] | Wu Wei, Mu Yi, Susilo W, et al. Certificate-based signatures: new definitions and a generic construction from certificateless signatures[C]//Edited by Chung K I, Sohn K and Yung M. Proc of WISA. Berlin: Springer-Verlag, 2008: 99-114. |
| [6] |
杨波, 肖自碧. 基于证书的签名方案[J]. 北京邮电大学学报, 2012, 35(5): 73–76.
Yang Bo, Xiao Zibi. Efficient certificate-based signature scheme[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(5): 73–76. |
| [7] | Boldyreva A, Palacio A, Warinschi B. Secure proxy signature schemes for delegation of signing rights[J]. Journal of Cryptology, 2012, 25(1): 57–115. doi: 10.1007/s00145-010-9082-x |
| [8] | Bellare M, Neven G. Multi-signatures in the plain public-key model and a general forking lemma [C]//Proc of CCS’06. Alexandria: ACM, 2006: 390-399. http://www.buptjournal.cn/CN/abstract/abstract1783.shtml |
| [9] | Pointcheval D, Stern J. Security arguments for digital signatures and blind signatures[J]. Journal of Cryptology, 2000, 13(3): 361–396. doi: 10.1007/s001450010003 |


