将多基站协作通信的功率分配问题转换为最大化系统容量问题,通过设置路径损耗门限为各用户判决与其通信的协作基站,并以最大化系统容量为目标,分别给出基于遗传算法和基于粒子群优化算法的多基站协作通信功率分配方案. 数值分析表明,当用户数量为100时,相对于多基站协作通信等功率分配方案,所提出的2种功率分配方案分别提高系统容量5.25bit·s-1·Hz-1和7.38bit·s-1·Hz-1. 另外,基于粒子群优化算法的功率分配方案在算法性能上优于基于遗传算法的功率分配方案.
Power allocation was formulated as the system capacity maximization problem and a strategy to solve the problem in its equivalent form was proposed. Based on genetic algorithm and particle swarm optimization, the path loss threshold to select the cooperative base stations for each user and maximize system capacity was set by the proposed power allocation strategy. Numerical results show that when the number of mobile users is 100, the proposed power allocation strategies based on genetic algorithm and particle swarm optimization will increase system capacity about 5.25bit·s-1·Hz-1 and 7.38bit·s-1·Hz-1 in the same conditions of adopting equal power allocation of multi-base cooperative communication system, respectively. Moreover, the algorithm performance of power allocation strategy based on particle swarm optimization is better than the power allocation strategy based on genetic algorithm.
随着移动用户数量的急剧增加以及用户对多种移动通信业务需求的不断增长,未来无线通信对系统容量有了更高的要求. 特别是在应对紧急突发事件的应急通信中,当通信量突发时,系统容量比其他性能指标显得更为重要. 多基站协作通信可以有效降低小区间干扰对边缘用户的影响,成为提升系统容量的有效手段[1].
协作通信系统性能的优劣与资源分配策略的选择密切相关,而功率分配问题又是资源分配的重要内容之一. 文献[2]研究了以最小基站总发射功率为目标的多基站协作通信最优功率分配方案,但没有从最大化系统容量的角度考虑功率分配问题. 文献[3]分析了OFDMA系统中两基站互为中继的协作传输策略,并使用注水算法给出基于最大化系统容量的功率分配方案,但没有涉及2个以上基站协作通信,且在功率分配时,并未考虑多个用户的复杂情况.
1 系统模型多基站协作通信系统模型中有N个移动用户,M个基站,每个用户和基站只配备单根天线. 系统中所有的基站按一定规则散布在覆盖区域内,通过光纤等高速传输介质与中央控制单元相连,各用户可以同时接收多个基站的发射信号. 假设无线信道服从准静态瑞利平坦衰落,则第n个用户的接收信号可以表示为
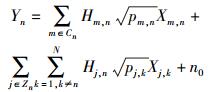
|
(1) |
式中:第1项表示有用信号,第2项表示干扰信号,第3项表示均值为0、功率谱密度为σ2的加性高斯白噪声(AWGN, additive white Gaussian noise). 其中:Cn为系统中所有与第n个用户进行通信的基站集合;Zn为系统中除Cn以外所有对第n个用户造成干扰的基站集合;Hm,n为基站m与用户n之间的传输信道;Xm,n为基站m对用户n的发射信号;pm,n为基站m发射给用户n的功率值,若第m个基站不与第n个用户通信,则pm,n=0.
假设各基站完全已知所有用户的信道状态信息,用Gm,n表示基站m与用户n之间的信道增益,则由式(1)可知,第n个用户接收信号的信干噪比(SINR,signal to interference plus noise ratio)可以表示为
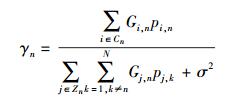
|
(2) |
多基站协作通信系统的容量可以表示为
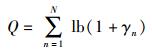
|
(3) |
在基站发射功率受限的情况下,多基站协作通信系统的功率分配问题可以转化为以最大系统容量为目标的最优化问题,即
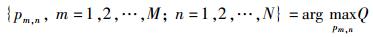
|
(4) |
同时各基站的发射功率满足
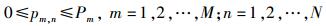
|
(5) |

|
(6) |
其中Pm为第m个基站的总发射功率.
2 功率分配方案 2.1 基站选择策略1) 比较用户n与各基站的路径损耗,将所有基站中与用户n之间的路径损耗最小的基站作为第n个用户的主服务基站,即
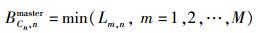
|
(7) |
其中:
2) 设置路径损耗门限β,将用户n到主服务基站以及到其余各基站的路径损耗的差值与β进行比较,为第n个用户确定其Cn中除
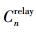
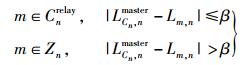
|
(8) |
其中
设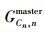
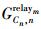
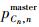
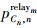

|
(9) |
将式(9)代入式(4),功率分配问题可重写为
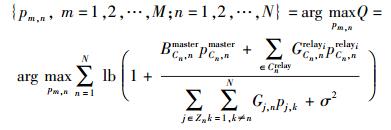
|
(10) |
式(10)中,一共有M×N个未知数,难以直接求解. 为了简化问题,可以将各用户主服务基站分配的功率作为参考,对其协作基站进行功率分配,使未知数的个数减少至N个. 可以将第n个用户的

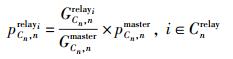
|
(11) |
将式(11)代入式(9),第n个用户的γn表示为
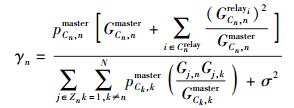
|
(12) |
将式(12)代入式(10),多基站协作通信系统的功率分配问题可以简化为

|
(13) |
上述多基站协作通信系统的功率分配问题是一个非线性优化问题,直接求解较为困难. 下面分别采用遗传算法和更加易于实现的粒子群优化算法对该问题进行求解.
2.2 遗传算法1) 编码与群体初始化
编码是设计遗传算法首先需要解决的问题[5],本方案采用实数编码方式,染色体的结构为
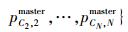
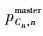
2) 适应度函数
适应度函数的形式直接决定群体的进化行为. 考虑式(13)的优化问题,适应度函数可以表示为
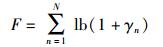
|
(14) |
3) 选择算子
选择操作以适应度值的大小为择优依据,从当前群体中选择适应度值高的染色体遗传到下一代群体中,并淘汰适应度值低的染色体. 采用轮盘赌选择策略,设染色体ai的适应度值为F(ai),群体规模为S,则染色体ai被选择遗传到下一代的概率为

|
(15) |
4) 交叉算子
交叉操作从群体中随机选取2个染色体作为父代以概率λc进行配对. 较大的λc可以增强算法开辟新搜索区域的能力,但算法已有的优良模式也更容易遭破坏,因此交叉概率λc的取值一般为[0.4~0.9][6]. 设r0为区间[0,1]上的随机数,则第i个染色体ai和第j个染色体aj交叉后的2个子代染色体为

|
(16) |
5) 变异算子
变异操作将染色体中某些基因座上的基因以概率λm进行变异. λm越大,群体的多样性越高,但过大的λm将使算法趋于随机搜索,因此变异概率λm的建议取值为0.001~0.1[7]. 第i个染色体的第j基因ai,j进行的变异操作为

|
(17) |

|
(18) |
其中:amax和amin 分别为ai,j的最大值和最小值,r1和r2为[0,1]区间的随机数,g和gmax 分别为当前迭代次数和最大进化次数.
2.3 粒子群优化算法设在d维搜索空间中,粒子群优化算法初始生成由S个粒子组成的种群O={O1,O2,…,OS}. 第i个粒子的位置为Oi=(oi1,oi2,…,oid)T,其速度为Vi=(vi1,vi2,…,vid)T. 每次迭代中,粒子通过跟踪个体极值Di=(di1,di2,…,dih)T和全局极值E=(e1,e2,…,eh)T来更新自己. 粒子更新其速度和位置的公式为
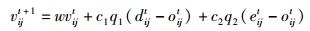
|
(19) |
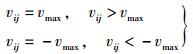
|
(20) |
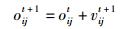
|
(21) |
其中:ω为惯性权重;t为迭代次数;vmax 为速度上限;q1和q2为[0,1]区间的随机数;c1和c2为学习因子,通常取c1=c2=2,在搜索过程中根据需要动态改变ω的取值[7].
3 数值分析首先,分别验证提出的功率分配方案在遗传算法和粒子群优化算法下的收敛性;其次,分析2种功率分配方案的性能优劣;最后,通过系统容量与用户数量的关系,将提出的2种功率分配方案与多基站协作通信等功率分配方案进行比较分析. 参数设置如表 1所示.
|
|
表 1 仿真参数及取值 |
图 1所示为M=6,N=100时,所提功率分配方案在遗传算法下的收敛性能. 从图 1可以看出,群体规模S=30时,由于群体多样性偏低,算法发生早熟现象;在S=60和S=100时,算法分别迭代47次和65次后收敛,体现出良好的收敛性能,且系统容量分别为70.39和70.68 bit·s-1·Hz-1.

|
图 1 功率分配在遗传算法下的收敛曲线 |
当M=6,N=100时,所提功率分配方案在粒子群优化算法下的收敛性能如图 2所示. 从图 2可以看出,群体规模S=10时,由于群体多样性偏低,算法发生早熟现象;在S=20和S=50时,算法分别迭代12次和15次后收敛,体现出良好的收敛性能,且系统容量分别为72.37和72.58 bit·s-1·Hz-1.

|
图 2 功率分配在粒子群优化算法下的收敛曲线 |
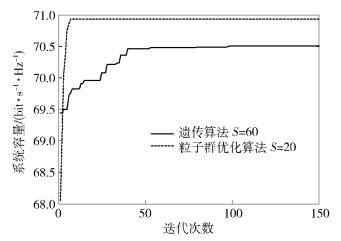
图 3所示为所提出的2种功率分配方案的算法性能. 设定M=6,N=100,在S=20时,粒子群优化算法迭代13次后收敛,最优解为70.93 bit·s-1·Hz-1;在S=60时,遗传算法迭代52次后收敛,最优解为70.51 bit·s-1·Hz-1. 从图 3中可以看出,在算法的收敛速度和求解最优值上,粒子群优化算法都优于遗传算法;同时,粒子群优化算法所需的种群规模远小于遗传算法,大大提高了算法的计算效率.
|
图 3 功率分配在2种算法的性能对比 |
系统容量与用户数量的关系如图 4所示. 设定M=6,考虑到遗传算法和粒子群优化算法在寻找最优解时具有一定的随机性,仿真中取10次独立实验的平均值. 从图 4中可以看出,用户数量由10增加到100,基于粒子群优化算法的功率分配方案、基于遗传算法的功率分配方案以及多基站协作通信等功率分配方案,系统容量分别增加45.71、44.83、42.38 bit·s-1·Hz-1. 当用户数量为100时,3种算法的系统容量分别为72.06、69.93、64.68 bit·s-1·Hz-1. 相比而言,所提出的2种功率分配方案在用户数量为100时,分别提高系统容量7.38和5.25 bit·s-1·Hz-1.

|
图 4 系统容量与用户数量的关系 |
将多基站协作通信系统的功率分配问题转换为最大化系统容量问题,分别给出了基于遗传算法和基于粒子群优化算法的基站发射功率分配方案. 数值分析结果表明,相对于多基站协作通信等功率分配方案,所提出的2种功率分配方案都可以有效提升多基站协作通信的系统容量. 此外,在算法收敛速度、最优解取值以及算法计算效率等方面,基于粒子群优化算法的功率分配方案都优于基于遗传算法的功率分配方案.
| [1] |
贾亦真, 陶晓明, 陆建华. 基于基站协作的空间应急通信系统及容量分析[J]. 清华大学学报: 自然科学版, 2011, 51(3): 405–409.
Jia Yizhen, Tao Xiaoming, Lu Jianhua. Spatial emergency communication system based on base station cooperation and its user capacity analysis[J]. Journal of Tsinghua University, 2011, 51(3): 405–409. |
| [2] | Phuyal U, Jha S C, Bhargava V K. Joint zero-forcing based precoder design for QoS-aware power allocation in MIMO cooperative cellular network[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(2): 350–358. doi: 10.1109/JSAC.2012.120214 |
| [3] | Wang Di, Li Zhaoquan, Wang Xin. Joint optimal subcarrier and power allocation for wireless cooperative networks over OFDM fading channels[J]. IEEE Transactions on Vehicular Technology, 2012, 61(1): 249–257. doi: 10.1109/TVT.2011.2175409 |
| [4] |
吕星哉, 王振, 朱近康. 分布式无线通信系统中的主从协同功控[J]. 电路与系统学报, 2010, 15(1): 59–64.
Lü Xingzai, Wang Zhen, Zhu Jinkang. Primary-subsidiary cooperative power control in ordered distributed wireless communication system[J]. Journal of Circuits and Systems, 2010, 15(1): 59–64. |
| [5] | Binelo M O, De Almeida A L F, Cavalcanti F R P. MIMO array capacity optimization using a genetic algorithm[J]. IEEE Transactions on Vehicular Technology, 2011, 60(6): 2471–2481. doi: 10.1109/TVT.2011.2158460 |
| [6] | Yuen S Y Y, Chow C K. A genetic algorithm that adaptively mutates and never revisits[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 454–472. doi: 10.1109/TEVC.2008.2003008 |
| [7] |
袁建国, 王琳, 黄胜, 等. 基于遗传算法的概率译码算法[J]. 北京邮电大学学报, 2012, 35(5): 98–101.
Yuan Jianguo, Wang Lin, Huang Sheng, et al. Probability decoding algorithm based on genetic algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(5): 98–101. |
| [8] | Zhan Zhihui, Zhang Jun, Li Yun, et al. Adaptive particle swarm optimization[J]. IEEE Transactions on System, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(6): 1362–1381. doi: 10.1109/TSMCB.2009.2015956 |



