2. 空军工程大学 信息与导航学院, 西安 710077
提出了一种针对威胁场景的风险评估方法. 首先构建了威胁场景的递阶层次化风险评价指标体系结构,定义了描述安全措施与风险形成关系的"不可控性"指标,增强了指标体系的完备性;其次定义了指标的高斯型隶属函数,在此基础上提出一种基于隶属度矩阵构造法的模糊综合评判模型,降低了评估过程中人为主观因素的影响;最后将上述模糊综合评判模型与层次分析法相结合对TS的风险度进行了量化计算. 通过实例分析表明该方法是科学的、有效的,为实现风险度大小排序提供了重要依据.
2. School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China
A risk assessment approach for threat scenario (TS) was proposed. Firstly, hierarchical index system of venture evaluation was constructed for TS, and a new index called uncontrollability was proposed to describe the uncontrollability of relationship between safety measures and risk formation, meanwhile, integrality of index system was enhanced. Secondly, membership function of indicators based on Gaussian function was defined, thereafter, an improved fuzzy comprehensive evaluation model based on membership matrix constructor method was given to reduce the influence of subjective factors. Finally, a combining method of fuzzy algorithm above and analytic hierarchy process were adopted to calculate the degree of risk quantitatively. The case study shows that this method is beneficial to risk size sort.
信息安全风险评估是一门以帮助人们评价网络风险、掌握风险规律为目的的学科. 目前主流的风险评估方法有攻击图法[1-2]、决策树分析法[3]、神经网络分析法[4]等. 这些方法各有优缺点及适用性,如攻击图法分析思路缜密、逻辑性强,适合规模较小的网络;决策树分析法通过逻辑关系图来确定树顶事件发生的原因和概率,方法较为繁琐,适用于拓扑结构较简单的系统;神经网络分析法具有超强的非线性映射能力,其局限在于需要大量的训练样本.
与上述方法相比,模糊综合评价法在处理大规模网络的多因素性、动态性、复杂性方面具有较强的优势. 文献[5-7]对基于模糊综合评价的风险评估方法进行了研究,取得了一定的成绩. 但仍然存在以下问题:一是对安全措施与风险形成的关系考虑不足,尤其缺少描述二者关系的评价指标体系,导致评估结果失准;二是模糊评价过程中对隶属度的确定方法往往采用专家评议法,增加了人为主观因素的影响. 为了解决以上2个问题,笔者提出了信息安全TS模糊风险评估方法.
1 构建层次化风险评价指标体系结构首先给出相关术语的定义.
定义1 威胁场景(TS):特定威胁主体(攻击者)可能利用某类系统脆弱性,从而给系统造成损失或影响的潜在危险情景;
定义2 发生概率(P):特定TS在系统环境下发生的可能性;
定义3 影响程度(E):特定TS实现后,给系统造成损失或影响的程度大小;
定义4 不可控性(T):特定TS规避系统控制策略或使策略失效的能力特性;
定义5 (RD):特定TS的风险测度值,用于度量风险大小.
TS的层次化风险评价指标体系结构如图 1所示. 图中目标层为被评价TS,如数据泄露、病毒入侵、未授权访问、非法篡改数据及拒绝服务攻击(DDoS)等. 准则层为“发生概率(P)”、“影响程度(E)”和“不可控性(T)”3个指标,其中“不可控性”指标是为了突出系统所采取安全措施对风险的消减和控制作用而首次提出的. 最后,将影响准则层各指标表现的因素进一步划分,构成指标层. 指标层各指标在此不再详述.

|
图 1 递阶层次化风险评价指标体系结构 |
采用层次分析法(AHP, analytic hierarchy process)计算指标权重.
首先,将指标间的相对重要度划分为9个等级,再以对上一层指标的影响程度为判断依据,对其所属的下一层指标进行两两比较,建立判断矩阵B,即
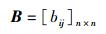
|
(1) |
其中:B为n阶方阵;n为下一层指标个数;bij为指标Bi对指标Bj的相对重要度,其取值为1~9之间的自然数或其倒数.
然后,根据判断矩阵B,利用方根法计算各指标的相对权重. 具体步骤为先求出B的特征向量M:

|
(2) |
其中

|
(3) |
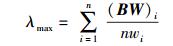
|
(4) |
最后,为了保证AHP得到的结论合理,需要对判断矩阵B进行一致性检验. 其公式为

|
(5) |

|
(6) |
其中:d为一致性指标,r为检验系数,g为平均一致性指标. 一般当r﹤0.1时,认为判断矩阵具有满意的一致性,否则需要调整判断矩阵,使之具有满意的一致性.
3 计算TS的模糊风险度由于评价指标较多,为了提高算法效率,分别对准则层和目标层进行2次模糊综合评判.
3.1 准则层指标模糊综合评判采用模糊综合评判法对图1中准则层指标P、E和T进行模糊评价,其基本步骤如下:
步骤1 确定因素集.
分别为指标P、E、T设置因素集为Up={I1~I5},Ue={I6~I9},Ut={I10,I11,I12}.
步骤2 构造隶属度矩阵.
对原有隶属度矩阵构造法进行了改进,提出了一种基于隶属函数的隶属度矩阵构造方法.
首先,为指标P、E和T分别定义一个在[0,1]区间的实数p、e和t,以代表P、E和T的量化值.
其次,为指标P定义隶属函数,用于描述指标P的取值p对不同评语vj(j=1,2,3,4,5)的隶属度. 这里不妨采用高斯隶属函数来反映正态分布特性,因此定义不同评语vj对应的隶属函数为
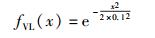
|
(7) |

|
(8) |
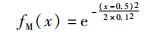
|
(9) |

|
(10) |

|
(11) |
为了便于表述,假设指标E、T对应的隶属函数也与P相同.
最后,考虑单因素Ii(i=1,2,3,4,5)对指标P的影响程度,并给出相应的量化值pi,pi∈[0,1];同理,得到ej(j=6,7,8,9)和tk(k=10,11,12). 将pi作为自变量代入式(7)~式(11),从而构造指标P的隶属度矩阵Rp:

|
(12) |
构造指标E的隶属度矩阵Re:
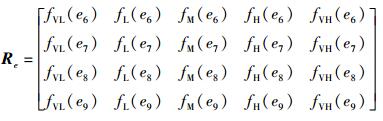
|
(13) |
构造指标T的隶属度矩阵Rt:

|
(14) |
步骤3 确定指标权重模糊集.
利用第2节所述AHP法确定因素集Up、Ue、Ut的权重模糊子向量分别为A1=(a1,a2,a3,a4,a5)、A2=(a6,a7,a8,a9)、A3=(a10,a11,a12).
步骤4 一级模糊综合评判.
确定指标权重和模糊隶属度矩阵后,即可得到指标P、E和T在评语集Vp、Ve和Vt上的模糊评价矩阵. 设其模糊评价矩阵分别为Bp、Be和Bt,则
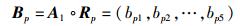
|
(15) |

|
(16) |

|
(17) |
其中

|
(18) |
其中i=j=1,2,…,5.
指标E、T的计算方法同上.
3.2 目标层指标模糊综合评判具体步骤如下:
步骤1 为目标层指标C(即被评价TS)确定因素集Uc={P,E,T},确定评语集Vc={v1,v2,v3,v4,v5},其含义分别为很低(VL)、低(L)、中等(M)、高(H)、很高(VH).
步骤2 二级模糊综合评判.
采用AHP法确定Uc的因素权重模糊子向量为W=(w1,w2,w3),从而构造二级综合评判矩阵为

|
(19) |
得到指标C的二级模糊综合评价矩阵K:

|
(20) |
步骤3 量化计算TS的风险度RD
首先以K中的隶属度ki作为权重系数;然后对评语集V进行等级赋值为Hv={h1,h2,…,hn},即等级vi对应数值hi,且等级vi从低至高时hi取值递增;最后得到被评价TS的风险度RD:
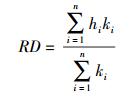
|
(21) |
被评价TS描述为:外部黑客利用系统弱点,通过缓冲区溢出的攻击方式非法登录至内部数据库服务器,企图窃取重要客户信息并植入后门木马病毒. 其中系统弱点:①操作系统(OS)版本过低,没有及时更新;②数据库系统存在弱口令. 此外,系统已采用安全措施:①入侵检测系统(IDS)持续运行;②防火墙设置了外部访问控制策略;③客户信息采用了MD5加密认证措施.
对该TS进行评价指标量化分析:其威胁动机是通过蓄意获取对方敏感信息以谋求商业利益最大化,动机很明显;威胁主体为计算机黑客,攻击能力一般;从已有安全防护措施强度看,攻击复杂度较大;上述系统弱点或漏洞的利用率较高;资产为重要客户信息,具有很强吸引力. 该TS可能对系统造成严重的机密性影响,而对完整性和可用性影响不大,但从影响范围及系统性能来讲,影响不算太大. 该TS的入侵途径隐蔽性一般,方式较为单一,突防能力较弱.
评价该TS风险度的具体步骤如下:
步骤1 定义目标层指标C对应的评语集及其量化值 V={v1,v2,v3,v4,v5}、Hv={0.1,0.3,0.5,0.7,0.9}.
步骤2 确定准则层指标P、E和T之间的相对重要度,建立判断矩阵

步骤3 方法同步骤2,确定指标层的相对权重子向量:A1=(0.3,0.2,0.1,0.1,0.3)、A2=(0.4,0.2,0.2,0.2)、A3=(0.2,0.2,0.6).
步骤4 根据上述指标量化分析,将指标层指标量化为p1=0.8,p2=0.5,p3=0.35,p4=0.6,p5=0.9,e6=0.95,e7=0.45,e8=0.45,e9=0.75,t10=0.5,t11=0.3,t12=0.4. 再由式(12)~式(20)得到指标C的二级模糊综合评价矩阵K=(0.000 1,0.066 8,0.59,0.222 5,0.261 2).
步骤5 由式(21)得到被评价TS的风险度RD=0.619,该值在v3与v4之间,因此判断TS的风险等级介于“中等”与“较高”之间.
5 算法优越性分析模糊综合评判是风险评估研究的重要方法之一. 该方法能将定性的评估转换为定量的评估,解决了区间法进行风险等级划分时带来的边界不合理问题. 但传统的模糊综合评判法在设置指标权重和指标隶属度的过程中往往采用专家评议法,降低了评估结果的客观性. 为了解决上述问题,笔者采用基于隶属函数的隶属度矩阵构造法,并将指标系统划分层次,采用AHP法确定指标权重,降低了人为因素的干扰. 另外,为了提高评价指标的完备性,提出的评价指标多达12个,结合AHP法对指标体系进行层次划分能使风险分析过程更加简单化. 最后,在准则层与目标层分别进行2次综合评判,提高了算法效率.
6 结束语构建了递阶层次化风险评价指标体系结构,其“不可控性”指标较好地描述了风险形成与安全措施的复杂关系. 另外,提出了一种针对TS进行风险评估的新方法,该方法以模糊综合评判为基础,采用基于隶属函数的隶属度矩阵构造法,并与AHP相结合,增强了评估结果的客观性. 最后,对特定TS风险度进行了计算,实现了风险大小排序,为系统选择风险控制策略提供重要指导.
| [1] | Ge Haihui, Gu Lize, Yang Yixian, et al. An attack graph based network security evaluation model for hierarchical network[C]//Yixian Yang. Proceedings 2010 IEEE International Conference on Information Theory and Information Security. Beijing: IEEE Press, 2010: 208-211. http://dl.acm.org/citation.cfm?doid=383059.383072 |
| [2] | Li Kai, Gu Naijie, Bi Kun, et al. Network security evaluation algorithm based on access level vector[C]//The 9th International Conerence for Young Computer Scientists. Hunan: [s.n.], 2008: 1538-1544. |
| [3] |
张利, 姚轶崭, 彭建芬, 等. 基于决策树的智能信息安全风险评估方法[J]. 清华大学学报: 自然科学版, 2011, 51(10): 1236–1239.
Zhang Li, Yao Yizhan, Peng Jianfen, et al. Intelligent information security risk assessment based on a decision tree algorithm[J]. Journal of Tsing hua University: Science and Technology, 2011, 51(10): 1236–1239. |
| [4] | Niu Honghui, Shang Yanling. Research on risk assessment model of information security based on Particle swarm algorithm-RBF neural network[C]//Circuits, Communications and System(PACCS). Beijing: [s.n.], 2010: 479-482. |
| [5] | Qu Zhiming. Application of comprehensive fuzzy evalua-tion in enterprise network security[ C] //Power Electron-ics and Intelligent Transportation System ( PEITS ).Shenzhen: [s. n. ], 2009: 54-57. |
| [6] |
吕镇邦, 周波. 基于 Shapley 熵和 Choquet 积分的层次化风险评估[J]. 北京邮电大学学报, 2009, 32(6): 83–87.
Lü Zhenbang, Zhou Bo. Hierarchical risk assessment based on shapley entropies and choquet integrals[J]. Journal of Beijing University of Posts and Telecommunica-tions, 2009, 32(6): 83–87. |
| [7] |
赵冬梅, 马建峰, 王跃生. 信息系统的模糊风险评估模型[J]. 通信学报, 2007, 28(4): 51–64.
Zhao Dongmei, Ma Jianfeng, Wang Yuesheng. Model offuzzy risk assessment of the information system[J]. Jour-nal on Communications, 2007, 28(4): 51–64. |


