2. 西安电子科技大学 测量与仪器系, 西安 710071
特高频率的测量是当前国际时频测控领域的研究热点.针对特高频率测量难、精度不易保证等问题,结合时空转换关系,提出了一种优于皮秒分辨率的特高频率测量方法.利用异频相位检测原理,把频率的测量转换为精密短时间间隔的测量,在短时间间隔测量中引入时间和空间的转换关系,利用信号传输延迟的稳定性,通过测量空间长度量获得延迟时间相位差,最终实现特高频率的测量.实验结果证明了该方法的有效性和可行性,在射频范围内其测量分辨率可达到10-12/s量级,与传统的频率测量方法相比,具有结构简单、成本低廉及测量精度高的特点.
2. Department of Measurement and Instrument, Xidian University, Xi'an 710071, China
The extra-high frequency measurement is a hot issue of research in the field of current international time-frequency measurement and control. Aiming at difficult measurement and uncertain precision of extra-high frequency in time and frequency measurement domain and combining time and space conversion relations, an extra-high frequency measurement in picoseconds was proposed. Utilizing different frequency phase detection principle, a precise short time interval measurement was changed into the measurement of frequency. By introducing conversion relations of the time and space and using stability of signal delay in the course of transmission, a phase difference of delay time was obtained based on measuring space length value. Furthermore, an extra-high frequency measurement could be achieved in the proposed method. Experiment shows that the measurement resolution of 10-12 within 1 s can be reached in radio frequency range. Comparing the traditional frequency measurement method, the proposed method features simple structure, low cost and high measurement precision.
随着航空航天、激光测距、精密定位、粒子飞行探测及其他高科技领域的技术发展,对高频率尤其是特高频率信号的测量精度提出了更高要求[1].目前国内外所使用的高精度频率测量方法主要是基于频率处理的测量方法,如模拟内插法、时间游标法、频差倍增法等.目前的频率测量方法在测量原理上没有发生大的变化,但在以前混频或谐波混频直接测频方法的基础上,结合微电子技术的发展及生产工艺有所改进[2].利用时间差比对的途径测量频率,对于频率信号间的相对测量是普遍适用的,尤其适合于频率稳定度较高的点频信号的高精度测量,且随着频率值的增加,测量的分辨率也将会大大提高.用异频相位检测原理,结合信号在延迟线中传输的高度稳定性和准确性,提出了一种优于皮秒分辨率的特高频率测量新方法.特高频率的精密测量不仅在微波量子频标方面而且对光频标的构成及研究都有重要意义.
1 测量原理 1.1 基于异频相位处理的频率测量原理大量实验结果表明,两异频信号可以通过其相互间的相位关系来探索它们之间的周期性变化规律,这种周期性变化规律是以等效鉴相频率、相位差群、群相位差、群周期及相位群同步等概念为基础的[3].
任意两异频信号f1和f2,若严格满足f1=Afmax,c和f2=Bfmax,c,其中A和B是2个互素的正整数,设A>B,则fmax,c为它们之间的最大公因子频率,fmax,c的倒数为最小公倍数周期Tmin,c,即
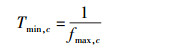
|
(1) |
两异频信号相位比对时,在任意Tmin,c内没有完全相同的相位差且相邻相位差在排列上不具有线性分布特征,因此不具备相位的可比性.但是若从最大公因子频率的数学意义上分析,相位差变化的结果必然以Tmin,c为间隔呈现周期性变化.也就是说,若把Tmin,c内所有的相位差作为一个群,打乱群内相位差的顺序,并按照相位差的大小重新排列,则发现这些相位差是按照量化步进的规律线性单调的.设量化步进值为ΔT,在A>B的情况下,这种相位差关系为ΔT、2ΔT, …, NΔT.实验结果证明量化步进的最大值NΔT为BΔT,恰好等于比对信号中频率较高信号的周期:

|
(2) |
重排后相位差的线性变化相当于2个相位不同步的频率信号以ΔT为分辨率相位跟踪的过程,故ΔT称为量化相移分辨率.当两信号之间的量化步进满足式(2) 时,在Tmin,c处会发生严格的相位重合.因此,由式(2) 可推出

|
(3) |
令fequ=ABfmax,c,则
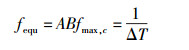
|
(4) |
这里fequ称为等效鉴相频率.等效鉴相频率反映了异频信号间的频率关系以及相位重合过程中相位差变化的快慢.由式(4) 可知,对于2个频率固定的信号,ΔT是个不变的值,它表示量化相位差的一个不可分割的最小的基本单元,有时也称为相位量子. fequ越大,ΔT越小,分辨率越高.在吉赫兹到太赫兹的等效鉴相频率下,可以获得皮秒甚至飞秒的测量分辨率.因此,在特高频率测量中,希望在大的频率差异下能拥有小的最大公因子频率.由等效鉴相频率表现出的相位比对通常称为异频鉴相.这里值得注意的是,异频鉴相建立在相位分析的基础之上,因此所有以最小公倍数周期为测量闸门且以等效鉴相频率为理论支撑的时间、频率及相位差测量和同步,均可获得较高的测量分辨率.由于外界的各种干扰,频率信号间存在相位扰动或频率漂移等现象.也就是说,f1和f2并不能严格保持A:B关系,而是具有微小相对频差Δf,由Δf引起的相位漂移为Δt.这使得相位比对时群与群以及群相位差之间会发生平行的移动,称为群相移.群相移的结果导致了群周期的产生,按群周期所进行的相位处理称为群周期相位处理,这种相位处理是任意频率信号下更具有代表性、更具有普遍意义的,如图 1所示.

|
图 1 任意信号之间的群周期相位处理 |
图 1中,以一个Tmin,c为间隔的重复性特征为基础,群内相位差以量化步进值Δt为分辨率呈现线性倍增.相位差Δt延迟的积累使得两异频信号在群周期处发生严格的相位重合.设发生严格相位重合的时间间隔为Tgp,称为群周期[4].由异频鉴相原理得知,必有Tgp=nTmin,c,也就是说,1个群周期由若干标称最小公倍数周期或者说群组成,且群相位差量化步进到满周期时所能达到的最大值nΔt恰恰等于一个相位量子,即nΔt=ΔT.实质上,群相位差变化的过程是两异频信号发生严格相位重合的过程.这种群相位差的变化规律是普遍的,它存在于任意异频信号之间,是异频相位检测、测量及处理的基础,同时也是对自然界中周期性运动现象做出本质性解释的表征.
图 1中的fout为鉴相输出结果.由式(4) 可知,在f1:f2严格成比例关系A:B时,ΔT为已知量,那么两异频信号的相对频差就可以表示为

|
(5) |
由式(5) 可知,异频相位比对方法开拓了一种测量特高频率的新思想,即在Δf已知的基础上,通过频率和时间间隔的对应关系,采用直接测量时间间隔的方法获得被测信号的频率,取代传统的基于频率处理的测量方法.如果能保证时间测量的精度,则高精度的特高频率的测量便易于实现.
1.2 电磁波信号的传输特性电磁波信号在空间或特定介质中的传输具有高度准确性和稳定性[5],若把这一固有的自然规律应用到频率测量中,将会提高频率测量准确度,如图 2所示.

|
图 2 时空转换关系实验装置 |
图 2中用正弦波作为信号源,以同轴电缆作为延迟线并被分为a、b、c, …,n个等间隔的检测点.用SR620时间间隔测量仪测出各检测点间的时间间隔,并与延迟线的长度间隔作一一对应,部分实验曲线如图 3所示.示出了10 MHz正弦波在间隔5 cm延迟线上对应的时间间隔.信号在延迟线上的传输整体上是线性的,且具有很好的稳定性.外部测量设备的介入可能会在微细范围内影响传输性能,但若屏蔽措施得当,对传输性能的影响将非常小[6].

|
图 3 信号在延迟线上传输的线性和稳定性 |
电磁波信号在同轴电缆线中的传输速度约为2×108 m/s,那么纳秒和皮秒的传输延迟分别为20 cm和0.2 mm.根据电磁波信号的传输特性,把其中一路信号进行延迟,使比对信号的相位重合点产生移动,通过提取和处理相位重合点边缘脉冲,达到特高频率的稳定测量.测量方案如图 4所示.

|
图 4 基于边缘重合脉冲的特高频率测量方案 |
由图 4所示,输入信号为高频信号fH和低频信号fL,为了便于测量,设两路信号的频率关系为fH=MfL+Δf, 其中Δf为两信号的相对微小频率差, M为标称频率下高、低频率的比值.由异频相位检测原理可知,高、低频率之间的标称最大公因子频率为fmax,c=fL,最小公倍数周期Tmin,c=1/fL=TL,相位量子ΔT=T1/B=1/fequ=TH.
高频信号经过放大电路后进入延迟传输线模块,低频信号经过整形电路和脉冲发生电路形成足够窄的尖脉冲信号fLP.在延迟线传输路径上每隔一定的距离v/MfL(1个延迟线传输模块)设置一路相位重合检测电路,这里,v表示信号在同轴电缆延迟线中的传输速度.通过低频脉冲信号对高频信号幅值的采样检测高频信号相位变化情况.检测结果中含有Δf信息,同时也反映高频信号频率值的情况.
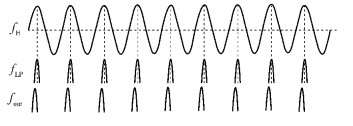
理想情况下的高频信号fH与低频信号fL成严格的整数倍关系,假设第1次相位重合检测电路检测到的是fH的波峰,由异频相位比对原理可知,之后每一路相位重合检测点必为fH的波峰,如图 5所示,其中fout为高、低信号相位重合检测的结果.
|
图 5 严格倍数关系的相位重合检测结果 |
在实际的相位比对中,由于相对频率偏差Δf的存在,那么波形的比对情况如图 6所示.

|
图 6 有频率微差的相位重合检测结果 |
在图 6中,因为存在由Δf引起的相位漂移Δt,使得相邻2个检测点之间的距离v/MfL对应的时间不再是TH.结合群相位差变化的规律性,Δt发生满周期变化的时间为TH,发生这样的变化所对应的时间恰恰为1个群周期[7].若群周期时间长度为τ,则τ必为TL的整数倍,代入式(5) 可得
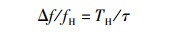
|
(6) |
图 5是图 6中Δt=0时的一种特殊情况,这种情况只有在fH严格等于MfL的情况下才能发生,此时式(6) 中的τ等于TL.在具体方案中考虑到信号在传输线中的损耗、延迟器件的速度以及噪声的影响,实验前需对传输线进行屏蔽隔离且采用无源同轴延迟导线.高频信号在延迟线中传输时,作为负载被每一个重合检测电路使用,因此在高频信号fH进入延迟传输线之前须对其进行放大处理,以保证有足够大的功率.另外,在传输线的末端添加匹配电阻,以防止高频信号在延迟线中的反射传播,同时延迟传输系统还应附加缓冲器,增强被测信号的驱动能力等.
4 实验及其分析根据图 4的设计方案,为实现2个频率成103以上倍数关系的频率信号之间的准确时间差比对,实验时采用了3235B铯原子钟、OSA8607B超高稳定度晶体振荡器及Agilent8664A精密频率合成器.
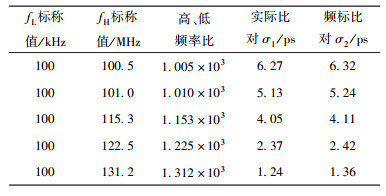
具体实验中由OSA8607B10MHz晶体振荡器作为Agilent8664A频率合成器的标频信号,合成输出10 kHz、100 kHz等一些与晶体振荡器有同样稳定度的低频信号fL.高频信号fH是以铯原子频标为基准合成的10~100 MHz以上的频率信号,并且可通过微调整铯原子频标的频率值,改变Δf的大小.在高、低频标比M为103以上时,很容易得到线性相位比对区域,提高比对精度.实验结果如表 1所示.
|
|
表 1 2种相位比对的实验结果 |
由表 1可知,实验结果与理论分析所达到的精度基本一致.微小频差Δf不同时,实际比对结果与频标比对测量结果有微小偏差,这种偏差是设备自身误差等因素引起的,不影响测量精度.可见,所提出的特高频率测量方法与频率的粗侧方法配合使用,即在两频率信号的比值M已知的情况下,可以实现高精度特高频率信号的测量.这里值得提出的是,本实验也可以通过李沙育图形法来实现,通过模拟示波上的李沙育图形,不仅可以观察出高低频信号或大频率比信号之间的频率关系,还可以得到频率稳定度的测量结果.
5 结束语针对特高频率测量难、精度不易保证等问题,提出了一种基于时空转换关系的特高频率测量方法.利用信号在延迟线中传输的稳定性及群周期变化的规律性,通过测量精度较低的长度量完成对短时间间隔高精度的测量,实现低频窄脉冲信号与高频信号幅值的重合检测,结合粗测频率值方法,最终算出特高频率的值.实验证明该方法可获得10-12/s量级的测量分辨率.
| [1] | Du Baoqiang, Dong Shaofeng, Wang Yanfeng, et al. High-resolution frequency measurement method with a wide-frequency range based on quantized phase step technique[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2013, 60(11): 2237–2243. doi: 10.1109/TUFFC.2013.6644729 |
| [2] | Du Baoqiang, Zhou Wei. Super-high resolution time interval measurement method based on time-space relationships[J]. Chinese Physics Letters, 2009, 26(10): 100601–100604. doi: 10.1088/0256-307X/26/10/100601 |
| [3] |
杜保强, 刘丹, 郭淑婷, 等. 基于时间间隔测量的宽范围高分辨率时间同步检测方法[J]. 电子学报, 2013, 41(6): 77–83.
Du Baoqiang, Liu Dan, Guo Shuting, et al. High-resolution and wide-range time synchronization detection method based on time interval measurement[J]. Chinese Journal of Electronics, 2013, 41(6): 77–83. |
| [4] |
周渭, 董绍锋, 杜保强. 长度游标与群周期比对相结合的频率测量方法[J]. 北京邮电大学学报, 2011, 34(3): 11–17.
Zhou Wei, Dong Shaofeng, Du Baoqiang. Super-high precision frequency measurement method combining length vernier and group-period phase comparison[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(3): 11–17. |
| [5] | Du Baoqiang, Zhou Wei, Dong Shaofeng. A group-period phase comparison method based on equivalent phase comparison frequency[J]. Chinese Physics Letters, 2009, 26(7): 0706021–0706024. |
| [6] | Kawagoe J, Kawasaki T. A new precision digital phase meter and its simple calibration method[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(2): 396–403. doi: 10.1109/TIM.2009.2024366 |
| [7] | Du Baoqiang, Wang Yanfeng. Ultra-resolution phase comparison method combining phase synchronous detection and common frequency source[J]. Measurement, 2013, 46(1): 374–377. doi: 10.1016/j.measurement.2012.07.011 |