为减少短喷泉码硬译码的延时和抖动,进行了理论分析和仿真优化.首先,推导了任意删除概率下硬译码延时和抖动的表达式,并分析了度数分布对这两者的影响;其次,针对几种典型短喷泉码,通过仿真优化降低了延时和抖动,其中,码长为1 024包的2种Raptor码的最小延时和抖动分别可优化至9.56%和3.22%,比现有短喷泉码有较大提升,具有较强的实用性.
Due to high flexibility to different channels, fountain codes with hard-decoding algorithm are used in many applications such as the board-band Internet. However, hard-decoding suffers from the delay and jitter caused by the randomness of encoding. The delay and jitter were minimized with analysis and computational optimization. Firstly, expressions of delay and jitter determined by degree distribution were deduced under any erasure probability. Secondly, several short-length fountain codes with small delay and jitter were developed from previous work through simulation and optimization. As a significant improvement, two raptor codes with length at 1 024 will offer minimized delay and jitter as 9.56% and 3.22%.
随着互联网业务的快速增长,传统信道编码和自动重传请求(ARQ, automatic repeat-request)面临着信道适应性低、译码复杂度高和重传延时长等问题[1-2].为此,Luby[3]在2002年提出喷泉码(fountain code)的概念,以一种随机分组的方式对信源数据进行编码,所产生的编码包是信源数据的线性随机组合. 2004年,Sharholaic[4]在路比变换(LT, Luby transform)码的基础上提出Raptor码,其译码性能较LT码有较大提高.喷泉码特有的随机编码特性使其无需获得信道的任何信息,在高噪声、强干扰等恶劣情况下,仍然具有良好的信道适应性.目前对喷泉码的应用研究主要集中在宽带互联网、无线广播网络和深空通信等方面.研究结果表明,喷泉码能显著减少重传所需的反馈,并能充分利用恶劣情况下信道的可用带宽[5-6].
喷泉码的译码方式分为硬译码和软译码.在加性高斯白噪声信道(AWGN, additive white Gaussian noise)下,通常采用以单位为比特的尽量接近信道容量的软译码方式[7].但是,仅当译码器与编码器严格同步时才能译码,所以在恶劣的信道情况下这种方式并不实用[8].更为广泛的方式是将信道等效成删除信道,并采用以包为单位的异步硬译码方式[9].硬译码的缺点是译码器的延时较大,对实时的通信业务造成影响;而且,延时是一个随机值,使译码器的输出产生抖动.
笔者在已有研究的基础上,推导了喷泉码在任意删除概率下硬译码延时和抖动的表达式,分析了度数分布对硬译码性能的影响,并针对几种典型短喷泉码(码长为16~1 024包)的硬译码性能,通过仿真进行优化,得出延时和抖动均小的喷泉码.
1 喷泉码的硬编译码原理LT码是一种非系统的喷泉码,对由k个数据包组成的信源数据[S1, S2, …, Sk],LT编码器可以生成任意数量n的编码包[B1, B2, …, Bn].每个编码包由d个数据包通过线性运算(异或)生成,并称编码包的度数为d. d是一个随机变量,其出现的概率取决于度数分布Ω.
Raptor码是对LT码的一种改进,在LT编码前先加一层低密度奇偶校验码(LDPC, low-density parity-check codes)预编码[b1, b2, …, bn],以提高译码的成功率.仿真结果证明, 利用一种简单的LDPC码进行预编码,即可达到较低的开销.
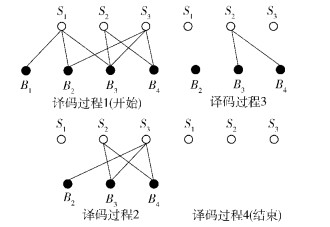
LT码的硬译码算法是一种简化的置信传播(BP, belief propagation)算法.如图 1所示,编码包到数据包的每一线段表示它们之间的异或运算关系.利用d=1的编码包(等于数据包)对d>1的编码包进行异或运算,每次运算使d减1.若k个数据包的d全部减到1,则译码成功结束[4].可见,LT码的译码过程与d密切相关,d过大或过小均不利于译码. Raptor码的译码过程与LT码类似,先用BP算法对LT译码,再对LDPC进行补充译码.
|
图 1 LT码译码过程 |
硬译码的延时和抖动主要受2个因素的影响:第1个因素是信道的删除概率,概率越大,延时和抖动也越大; 第2个因素是喷泉码本身的度数分布. LT码和Raptor码的度数分布设计均是启发性的,在码长足够大的情况下有较好的译码性能[3-4],但未达到最优.进一步的研究是把译码过程等效为Markov链,并利用其转移矩阵推导译码开销的表达式,再计算最优的度数分布.但是,随着码长的增大,转移矩阵的阶数成超几何级数增大,当码长大于4时无法计算.当只考虑接收编码包数量等于数据包数量的特殊情况时,计算可稍简化,并得到次优的度数分布.但是计算量也随码长增大成几何级数增大,只对码长为20以内的喷泉码适用[9].目前实用码长喷泉码的设计仍以仿真为主,即对译码器输入足够数量编码包的随机组合,遍历译码器的所有状态,然后根据仿真结果对设计进行修改[9-10].
硬译码方式下,编码器随机地产生n个编码包,直到译码器成功译码时,发送反馈到编码器终止编码.由于每个编码包均加入如32位循环校验等的检错码,所以通过检错的编码包被认为是无差错的[9].在删除信道下,通过n的分布可以直接推导延时和抖动的表达式.
定义1 对于码长为k的喷泉码,在固定删除概率θ(0≤θ≤1) 下,分别定义n、m为成功译码所需编码器发送的编码包数量、译码器接收的编码包数量.
定义2 分别定义Pr (n)、Pr (m)为成功译码的事件合集中某一n、m值出现的概率.
定义3 定义Pr (n|m)为译码器接收m个编码包并成功译码的条件下,编码器发送n个编码包的概率.
定义4 定义n的平均值为〈n〉,方差为〈n2〉; m的平均值为〈m〉,方差为〈m2〉.
定义5 定义硬译码的延时为ε=〈m〉/k-1,抖动为 
为说明喷泉码的硬译码抖动与σ值之间的关系,以文献[9]的一个Raptor码(k=1 024) 为例,在大于平均值的σ、2σ、3σ的3个范围内,Pr(m)分别包含了86.5%、96%、99%的不同m值,与正态分布类似.这说明,在99%的成功译码概率下,该Raptor码的译码过程要等待额外297个编码包的传输时间.下面将通过上述定义,推导ε和σ的表达式.
由定义2可知,Pr (m)是喷泉码未经过删除信道的译码特性,只与Ω有关,与信道无关.而Pr (n)是喷泉码经过删除信道的译码特性,与信道相关,由此可得
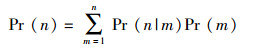
|
(1) |
其中,Pr (n|m)代表删除信道特性,Pr (m)代表喷泉码特性.根据定义3可得

|
(2) |
式(2) 所描述的现象为编码器在发送了前n-1个编码包后,译码器只收到其中未被删除的m-1个编码包,译码未成功.而当编码器发送第n个编码包时,该包未被删除.译码器接收到该包后,译码成功.将式(1)、式(2) 合并,得到
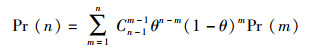
|
(3) |
根据式(3) 和定义4、定义5,可得
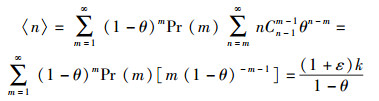
|
(4) |
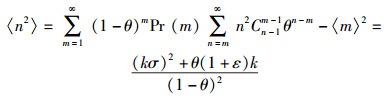
|
(5) |
为验证式(4)、式(5) 的正确性,对文献[10]中一个已知ε值的次优LT码(k=16) 进行译码过程的106次仿真,得到其在不同删除信道中(θ=0, 0.2, 0.6) 的性能.经比较,仿真结果与式(4)、式(5) 的理论值完全吻合.
式(4) 表明,〈n〉仅与θ成简单的线性反比关系,具有较小ε值的喷泉码通过任意删除信道后,〈n〉值仍然较小.而式(5) 表明,〈n2〉不仅与σ成正比,还与θε成正比.这说明,ε值和σ值均小的喷泉码才能在删除信道下有较小的〈n2〉值.删除信道中,噪声和干扰均可等效成信道的删除概率θ.当θ增大时,〈n〉和〈n2〉随之增大,但这种增长仅与θ成线性反比关系,证明喷泉码对信道具有良好的适应性.而且当编码包的包长足够小、喷泉码的码长足够大时,θ接近比特的出错概率,ε值也接近0,喷泉码可以接近信道容量.所以,在设计喷泉码时,不需要对不同的删除概率调整度数分布Ω,仅需对ε和σ进行优化.
3 度数分布对硬译码性能的影响确定了〈n〉、〈n2〉与ε、σ的关系后,讨论ε和σ的优化.由于译码过程是一个随机过程,而且译码器的每一状态只与前一状态和当前接收到的编码包有关,所以可以等效成一个Markov链.其转移矩阵的元素是各种译码状态出现的概率.这些概率均由Ω推导而来,ε值和σ值的表达式实际上就是Ω的函数.在文献[10]的基础上,将表达式的推导从一阶的ε扩展至二阶的σ.以k=3的LT码为例,Ω=[Ω1, Ω2, Ω3],利用转移矩阵得出[10]

|
(6) |
扩展至二阶,则得

|
(7) |
当k=4时,ε、σ表达式的项数均超过50项,未在此详细列出.分别对k=3、4时的LT码进行优化,在{0<Ω1<1, 0<Ω2<1, Ω1+Ω2<1}的范围内取值,分别令ε、σ最小,结果如表 1所示.
|
|
表 1 LT码(k=3、4) 的ε值和σ值仿真结果 |
文献[10]中提出,ε作为Ω的函数,存在一个函数值的平缓区域.在此区域内,不同Ω取值下的ε值均相当接近.利用式(7) 对σ值进行分析,发现σ值也存在平缓区域.以上述k=3、4的LT码为例,由表 1可见,令ε、σ分别最小的2种Ω取值差别很小.这说明,ε值和σ值均小的喷泉码是存在的.进行仿真优化时,可先以较大的步长进行,得到平缓区域的大致范围,再以较小的步长在此区域内进行精确仿真,得到最小值.这种改进的仿真方法能大量节省仿真次数.
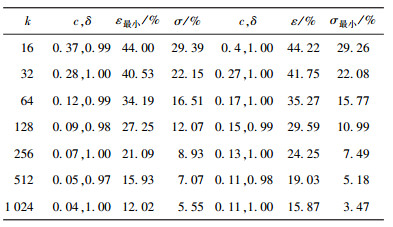
4 对几种典型短喷泉码的仿真优化 4.1 对典型LT码的优化Luby提出的典型LT码的Ω是固定的Ideal Soliton分布和可调节的Robust Soliton分布的组合.通过调节Robust Soliton分布的参数c和δ[3]可以使译码过程更容易开始并更加稳定,得到ε和σ均小的LT码.对实用码长为16~1 024包的典型LT码的译码过程分别进行106次仿真后,得到ε和σ分别最小的2种LT码,如表 2所示.
|
|
表 2 典型LT码(k=16~1 024) 的ε值和σ值仿真结果 |
由表 2可知,随着k的增大,ε和σ减小,但减小的趋势更平缓.当k趋近无穷大时,ε和σ均可趋近于0.
文献[10]中提出了k=16的经过理论推导的次优LT码,ε=42.81%,σ=30.1%.优化后的典型LT码的σ值已经小于次优码,但ε值仍然稍大于次优码,这说明两者性能已经接近.
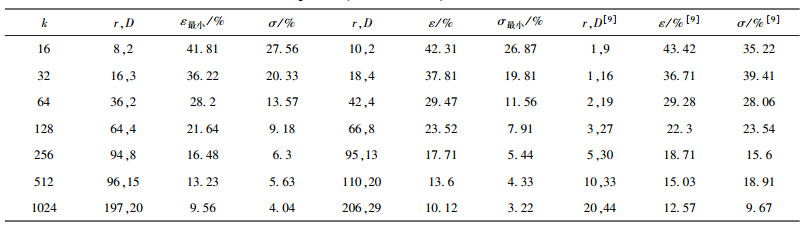
4.2 对典型Raptor码的优化Raptor码在同等长度下比LT码的硬译码性能更好.由于文献[9]中Raptor码的Ω已经过充分优化,这里不对Ω进行修改,仅对其LDPC码的冗余长度r和冗余节点的度数D进行调整,得到的优化结果如表 3所示.
|
|
表 3 典型Raptor码(k=16~1 024) 的ε值和σ值仿真结果 |
表 3中附有文献[9]的短Raptor码的仿真结果.可见,优化后的Raptor码对比文献[9]的Raptor码,ε值减小1%~3%,σ值减小6%~19%.特别是k=1 024的2种Raptor码,其最小ε值仅为9.56%、最小σ值仅为3.22%,性能比文献[9]中分别提高了3.01%和6.45%,提升幅度较大.所以,优化后的Raptor码能大幅减小译码器的延时和抖动,使其应用场合更加广泛.
5 结束语采用理论推导与计算机仿真结合的方式,得到硬译码延时和抖动均小的码长为16~1 024包的短喷泉码.其中,码长为1 024包的2种Raptor码的最小延时和抖动分别为9.56%和3.22%,比现有短喷泉码的性能有较大提升,具有较强的实用性.未来的研究将集中在利用硬件发挥其良好的译码性能.与现场可编程门阵列(FPGA, field programmable gate array)相结合后,可实现结构简单、高速运行的短喷泉码异步译码器,在各种恶劣信道中提供高速、可靠、接近信道容量的宽带应用.
| [1] | Lee S, Liu Y, Chiu H, et al. Fountain codes with PAPR constraint for multicast communications[J]. IEEE Trans Broadc, 2011, 57(2): 319–325. doi: 10.1109/TBC.2011.2104690 |
| [2] | Badarla V, Subramanian V, Leith D. Low-delay dynamic routing using fountain codes[J]. IEEE Commun Lett, 2009, 13(7): 552–554. doi: 10.1109/LCOMM.2009.081997 |
| [3] | Luby M. LT codes[C]//Proc 43rd Annual IEEE Symp Found Comput Sci. 2002: 271-280. |
| [4] | Shokrollahi A. Raptor codes[C]//Proc Int Symp Inform Theory. 2004: 36. |
| [5] | Byers J W, Luby M, Mitzenmacher M, et al. A digital fountain approach to asynchronous reliable multicast[J]. IEEE J Sel Area Commun, 2002, 20(8): 1528–1540. doi: 10.1109/JSAC.2002.803996 |
| [6] | Chieochan S, Hossain E. Wireless fountain coding with IEEE 802.11e block ACK for media streaming in Wireline-cum-WiFi networks: a performance study[J]. IEEE Trans Mobile Comput, 2011, 10(10): 1416–1433. doi: 10.1109/TMC.2010.251 |
| [7] | Mackay D J. Fountain codes[J]. IEE Proc Commun, 2005, 152(6): 1062–1068. doi: 10.1049/ip-com:20050237 |
| [8] | Abdulhussein A, Oka A, Lampe L. Rateless coding for hybrid free-space optical and radio-frequency communication[J]. IEEE Trans Wireless Commun, 2010, 9(3): 907–913. doi: 10.1109/TWC.2010.03.090108 |
| [9] | Zhang W, Hranilovic S, Shi C. Soft-switching hybrid FSO/RF links using short-length raptor codes: design and implementation[J]. IEEE J Sel Area Commun, 2009, 27(9): 1698–1708. doi: 10.1109/JSAC.2009.091219 |
| [10] | Hyytia E, Tirronen T, Virtamo J. Optimal degree distribution for LT codes with small message length[C]//IEEE 26th Int Conf Comput Commun. 2007: 2576-2580. |