针对分布式系统的特点,提出了一种基于网格空间的测度属性关联度计算方法,并以此建立了网络模型来刻画分布式系统测度属性的关系;提出了基于隐马尔可夫模型的测度属性关系网络划分方法;利用最新监测的属性关联度信息,设计了基于测度属性关系网络划分的分布式系统异常检测算法;对多种攻击进行异常检测实验,从而验证了提出方法的有效性.
The anomaly detection methods based on measurement attributes relationship analysis is proposed. The correlation between the measurement attributes in space grid structure is calculated, and hereby the relationship network model of measurement attributes is established. The network segmentation method is put forward based on hidden Markov model. The anomaly detection algorithm for distributed systems is designed by using the newest monitoring attributes correlation. The anomaly detection experiments demonstrate the effectiveness of the proposed method.
分布式系统的硬件资源、通信资源、软件及信息资源等容易遭到破坏、更改、功能失效等事件,使分布式信息系统处于异常状态[1].国内外的研究学者对信息系统异常检测方法包括:1) 基于安全模式的异常检测技术[2];2) 协议异常检测技术;3) 数据流量异常检测[3].然而分布式系统的特点无法直接应用现有的方法[4].目前研究学者建立了基于关联性的异常检测模型[5-7],但现有的工作只集中在单一的关联类型,因而不能准确地描述整个分布式系统,并且缺少对测度属性的时间相关性分析.
1 测度属性关系网络模型定义1 测度属性是构成分布式系统中与计算机运行紧密相关的可测量属性,如:Ⅰ/O吞吐量等.
分布式系统中所处理业务具有的流程相关性使各计算机的测度属性满足一定的关联,这种关系可通过对测度属性的历史数据分析得到.因此本研究首先给出分布式系统主机间测度属性关联度的计算方法.
1.1 测度属性的网格映射在时刻t,将2个测度属性值q1, q2看做一个2维特征向量xi=(q1, q2),首先建立描述数据x1, x2…, xt, …的相关性模型M,假设x取自一个2维有限数值空间,将这个空间分割为若干个非重叠的矩形单元网格,所有这些非重叠矩形单元的集合形成一个网格结构G=(c1, c2, …, cp).
首先取一个维度上的上下界构成一个区间,然后将这个区间以单位长度的大小进行分割,并计算落入每个单元内点的数量B,如果B对于事先设定的分布相似阈值β是相似的,则合并临近的单元格,对每一维度都采用以上过程来获得所有的网格.在更新过程中,大部分情况下一个新的观测值xt+1落入网格结构G其中的一个网格中,然而xt+1也可能超出这个范围(上界即为u).由于监测数据通常是逐渐变化的,所以当xt+1与网格的边界的距离在一定范围内才进行更新,首先需要计算历史数据中数据的平均间隔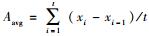
用贝叶斯理论计算测度属性对的概率转化过程,为了方便讨论,使用P(xt→xt+1)代表P(xt+1|xt),用P(ci→cj)代表P(xt+1∈cj|xt∈ci).因此有P(ci→cj|D)=P(D|ci→cj)P(ci→cj)/P(D),其中D是历史数据集,由于推导从ci到cj的概率转化过程与P(D)无关,可以忽略.有P(ci→cj|D)∝P(ci→cj)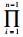
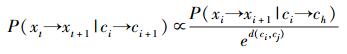
|
(1) |
其中:xt+1∈ch,xt∈ci;d(ci, cj)是ci到cj的距离;e为概率衰减的比例.因此有
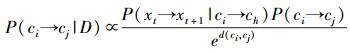
|
(2) |
根据约束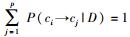
对于时间t+1的测度属性qa和qb,设从时间1到t监视数据的更新模型为Mt+1a,b. x表示包含来自qa和qb的测量值的2维特征向量.在t+1时刻,模型Mt+1a,b输出ci到网格结构中任何单元cj的转化概率.定义等级函数
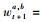

采用无监督算法发现测度属性的异常情况.隐马尔可夫随机场(HMRF,hidden Markov random field)理论是一种研究分析物理现象的空间或时间相关特性的概率理论.
2.1 测度属性关系网络划分算法首先,将测度属性构成的关系网络模型表示为图G=(V, W),V表示测度属性节点{v1, v2, …, vm},W是对称的m行m列的网络邻接矩阵,其中wij=wi.j是2个对象vi和vj连接的平均关联度.
HMRF模型具有如下特征.
1) 隐含划分符号
Z={z1, z2, …, zm}是一组隐含随机变量,其值是不可观测的.每个变量zi表示vi的划分.设有K个划分,那么zi∈{0, 1, …, K}.
2) 邻近系统
权重为W的连接可以在隐含符号中推导出依赖关系,如果2个对象vi和vj的关联度超过设定的阈值χ,那么它们属于相同的划分的概率较大.然而,离群点是随机产生的,所以离群点的邻近点不一定仍是离群点.因此将邻近关系系统调整为

|
这里Ni代表对象vi的邻近点集.当zi≠0时,那么vi的邻近关系在G中包含正常的邻近点.
3) 隐含变量间的依赖
在隐含变量Z上定义的随机变量场,是一个马尔可夫变量场,满足马尔可夫属性
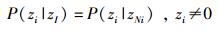
|
该式表明,如果zi和一个共同体对应,zi的概率分布仅依赖于vi在G中的邻近点的符号.如果zi=0,vi是离群点,且没有和该随机场中的其他任何对象的关联度超过χ,使P(zi=0)=η(η是一个常量).通过Hammersley-Clifford定理,马尔可夫随机场(MRF,Markov random field)可以相当于具有吉布斯分布的特征
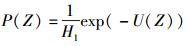
|
(3) |
其中:H1是规格化常量,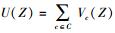

|
(4) |
其中:λ是常量,wij表示2个对象vi和vj之间有连接,而且zi和zj都不等于0. δ函数定义如下:如果x=0, δ(x)=1;否则,δ(x)≠0.
本研究的目标是寻找概率最大化的测度属性划分符号,Z={z1, z2, …, zm}.基本思路是保持其他对象的符号固定,并按顺序更新每个对象的符号.通过最大化P(zi|zI-{i})来更新zi.下面讨论当zi取非0或者0值时的2种情况.
1) 如果zi≠0,有P(zi|zI-{i})∝P(Z).
由式(3) 和式(4) 得出Z的概率分布为
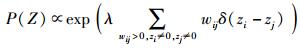
|
(5) |
在P(zi|zI-{i})中,包括除了vi以外的对象的连接都是不相关的,因此有
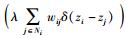
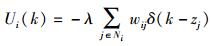
|
(6) |
2) 如果zi=0,vi没有邻近点,因此
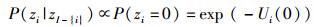
|
(7) |
且有Ui(0)=-ln(η)=a.因此,找到使P(zi|zI-{i})最大化的zi,等价于使能量函数最小化,即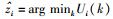
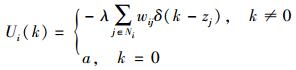
|
(8) |
测度属性关系网络划分算法如下.
输入 关联矩阵W,划分数K,阈值a,属性数m
输出 关系划分后的隐含符号Z
1 int t=0, i=1, k=0; //更新次数、循环控制参数
2 Randomly set variable Z0; //随机集合Z0
3 while(Ztis not close enough to Zt+1) {
4 t=t + 1;
5 for(i=1; i < = m; i ++) {
6 for(k=0; kK; j ++)
7 Calculate Ui(k) using formula 6;
8 if(Ui(k) > a) zit= 0;//为离群点
9 else {zit=k which k has minimal Ui(k); }}}
10 return Zt
使用平均Silhouette(Sil)指标来评价K值,另a(t)为划分Zj中的测度属性t与类内所有其他样本的平均关联度,d(t, Zi)为测度属性t到另一个划分Zi的平均距离,则b(t)=min {d(t, Zi)}, i=1, 2, …, k, i≠j,每个测度属性的Sil指标为Sil(t)=(b(t)-a(t))/max {a(t), b(t)}.
2.2 分布式系统异常检测算法分布式系统测度属性的数据在时序上是相关的,系统在正常情况下划分结果不会发生改变,因此系统的异常可以通过这种划分结果的变化来体现.
测度属性关系分析的异常检测算法如下.
输入 测度属性划分的隐含符号Z={z1, z2, …, zm},阈值a,最新的测度属性值i与其他测度属性值的关联度wij,其中j=1, 2, …, m且j≠i
输出 测度属性异常检测符号A={a1, a2, …, am}
1 int t=0, i=1, k=0; //更新次数、循环控制参数
2 for(i=1; i < =m; i ++) {
3 for(k=0; k < =K; j ++)
4 calculate Ui(k) using formula 6;
5 if (Ui(k) > a) zi′= 0;
6 else {zi′=k which k has minimal Ui(k); }
7 if(zi! =zi′)//划分结果发生变化
8 ai=1;}
9 Updata Z=Z′;
10 return A;
在测度属性异常检测符号A={a1, a2, …, am}中,若对应位置为1,则表明该测度属性异常.该算法的时间复杂度为O(Km),其中K为类的个数,m为测度属性的个数.异常检测算法包括网格生成和异常检测2部分,因此其总的时间复杂度为O(2m2n+Km)=O(m2n).
3 实验与分析选取了实验室环境中具有16个计算机节点的服务器集群,包括:网页服务器8台;数据库服务器4台;应用服务器4台.选取中央处理器使用率、内存使用量等40个测度属性进行实验.为了体现在不同情况下的测试结果,使用Nessus-3.2作为漏洞扫描工具,使用Coral-3.7.5记录测度属性值. 图 1显示了分布式系统的并发访问量与训练数据集长度的检测模型测试结果.当分布式系统并发访问量增加时,需要使用更长时间的训练集进行训练,以保证建立稳定的检测模型,如果训练时间太短会使数据稀疏导致模型过于敏感,误报率较高.训练时间长度为一周时,达到稳定.

|
图 1 训练集长度与系统访问量之间的关系 |
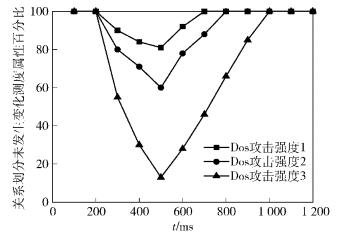
选择3种拒绝服务(Dos,denial of service)攻击强度进行了对比实验,如图 2所示.攻击强度1为1万个链接/s、攻击强度2为2万个链接/s、攻击强度3为3万个链接/s,攻击从300ms开始,到500ms结束.从图 2可知,不同的攻击强度造成的异常检测效果不同,攻击强度低时导致部分同类功能的计算机测度属性关系变化明显.当DoS攻击强度达到一定程度时,大部分计算机的测度属性关系都发生了变化,并且随着攻击强度的增加,攻击恢复的时间也会增加.如在攻击强度3时,恢复时间的长度是攻击的2倍.这是因为系统进行恢复时,系统受到对缓存中的攻击数据进行后续处理的影响,同样也会导致关系划分需要从异常转变到正常的过程.
|
图 2 拒绝服务攻击对比实验数据 |
U2R(user to root)攻击是用户获取超级权限的攻击.可通过暂停被控制主机的服务方式进行模拟实验,如图 3所示.其中U2R攻击强度分别为:控制1台计算机、2台计算机和4台计算机.

|
图 3 U2R攻击对比实验数据 |
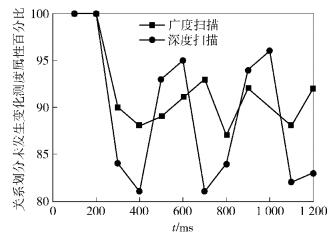
从图 3可知,攻击强度的增加会使关系发生变化的测度属性数量同时增加,但不同U2R攻击强度的恢复时间基本一致,这是因为主机恢复工作的时间基本一致.探测(PROBE)攻击是一种探测类攻击,根据探测方式的不同可以分为广度探测和深度探测,图 4给出了用2种扫描进行异常检测的对比实验.
|
图 4 PROBE攻击对比实验数据 |
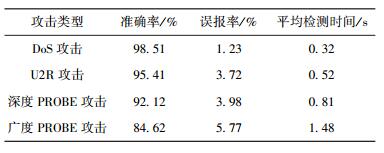
分析图 4可知,由于广度扫描分散了扫描数据对系统的影响,所以对系统的影响比较小.而深度扫描针对每台计算机进行探测, 导致该计算机的测度属性关系变化较大,因此深度扫描的异常检测指标在广度扫描的检测指标上下波动.本研究使用一周的数据训练,对所提出的检测方法在多种攻击事件中进行了统计测试,在实验环境中对每种攻击分别进行1000次(共10组)实验,平均检测结果如表 1所示.
|
|
表 1 检测方法性能分析表 |
分布式系统的资源分布化、计算分布化的特点使得传统的异常检测方法无法直接应用.本研究的主要贡献有:1) 提出了刻画分布式系统测度属性关系的网络模型;2) 设计了分布式系统测度属性关系网络的划分算法;3) 提出了基于测度属性关系网络划分的异常检测算法.下一步的工作主要是设计融合测度属性关系和属性测量值的划分方法等.
| [1] | Chandola V, Banerjee A, Kumar V. Anomaly detection: a survey[J]. ACM Computing Surveys, 2009, 41(3): 1–58. |
| [2] |
张晓惠, 林柏钢. 基于特征选择和多分类支持向量机的异常检测[J]. 通信学报, 2009, 30(10A): 68–73.
Zhang Xiaohui, Lin Bogang. Anomaly detection based on feature selection and multi-class support vector machines[J]. Journal on Communications, 2009, 30(10A): 68–73. |
| [3] | Torres R, Hajjat M, Rao S G, et al. Inferring undesirable behavior from P2P traffic analysis[C]//Proceedings of the Eleventh International Joint Conference on Measurement and Modeling of Computer Systems. Seattle: ACM, 2009: 156-167. |
| [4] |
钟尚勤, 徐国胜, 姚文斌, 等. 基于主机安全组划分的网络安全性分析[J]. 北京邮电大学学报, 2012, 35(1): 19–23.
Zhong Shangqin, Xu Guosheng, Yao Wenbin, et al. Network security analysis based on host-security-group[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(1): 19–23. |
| [5] | Chen M Y, Kiciman E, Fratkin E, et al. Pinpoint: problem determination in large, dynamic internet services [C]//Dependable Systems and Networks, 2002(DSN 2002). San Francisco: IEEE, 2002: 595-604. |
| [6] | Bahl P, Chandra R, Greenberg A, et al. Towards highly reliable enterprise network services via inference of multi-level dependencies [C]//ACM SIGCOMM Computer Communication Review. Seattle: ACM, 2007: 13-24. |
| [7] | Munawar M A, Jiang M, Ward P A S. Monitoring multi-tier clustered systems with invariant metric relationships[C]//The 2008 International Workshop on Software Engineering for Adaptive and Self-managing Systems. Seattle: ACM, 2008: 73-80. |