为了分析大规模天线系统能效与谱效、基站天线个数及小区半径间的关系,为实际通信系统参数设置提供理论依据,针对采用迫零检测算法的上行大规模多输入多输出系统,引进实际功耗模型,推导出能效与谱效、接收天线个数及小区半径间的闭式关系,进而根据此闭式得到系统的最优能效、相应的谱效和消耗的功率.仿真结果表明,合理的谱效工作点设置、增加基站接收天线个数和减小小区半径是增强系统能效的重要手段.
Analyzing the relation among energy efficiency, spectrum efficiency, the number of antennas at the base station and cell radius is helpful to the parameter design of the practical communication system. When zero-forcing detector was adopted in the uplink massive multiple-input multiple-output system, the closed-form expression among energy efficiency, the spectrum efficiency, the number of receiving antennas and the cell radius were derived according to the realistic power consumption model. Further, the optimal energy efficiency, corresponding spectrum efficiency and power consumption were deduced based on the closed-form. It is shown that the setting up of rational spectrum efficiency, the deploying of more receiving antennas at the base stations and the shrinking of cell radius are three key measures to enhance the system energy efficiency.
随着无线通信网络引起的二氧化碳排放量和运营商运营资本的增加,能效成为通信系统重要的衡量指标[1].大规模多输入多输出(massive MIMO, massive multiple-input multiple-output)系统被认为是提高下一代无线通信系统容量、能效和可靠性的重要技术[2].前期研究结果表明,迫零(ZF, zero-forcing)算法是折中系统容量和复杂度的高效线性预编码和检测算法[3-4].但在ZF检测算法下上行massive MIMO的理论能效尚未给出[2-3].
为了研究采用ZF检测算法的上行massive MIMO系统能效,首先引进实际的功耗模型[5],包括发射功率和电路功率,结合ZF检测算法的上行massive MIMO系统谱效[3],推导了能效与谱效、接收天线个数和小区半径间的闭式关系.进一步,根据凸优化理论,求得系统的最优能效、相应的谱效和功率消耗.仿真结果表明,合理的谱效工作点设置、增加接收天线个数和减少小区半径可以增强系统能效,同时结果容易扩展到下行massive MIMO系统,并为系统参数设计提供理论依据.
1 Massive MIMO系统模型和谱效考虑一个上行massive MIMO系统,如图 1所示,基站和用户终端分别架设N根和单根天线.有K个均匀分布在小区半径为R的用户同时同频向基站发送信息.

|
图 1 massive MIMO系统模型 |
假设从K个用户到基站的信道为G=HD1/2,D=diag{β1, β2, …, βK}为大尺度衰落矩阵,由路径损耗和阴影衰落组成,即βk=φdk-αζ.其中:φ为与载波频率、天线增益有关的常数,dk为用户k和基站间的距离,α∈[2, 6]为路径损失指数,ζ为服从对数正态分布的阴影衰落,即
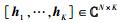
基站的接收信号为
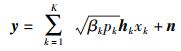
|
(1) |
其中:pk和xk分别为用户k的发射功率和归一化调制符号,n~CN(0N, σ2IN)为基站的加性复高斯噪声.
假设用户在补偿大尺度衰落后,采用等增益系数ρ0进行信号发射,即
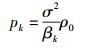
|
(2) |
设用户和基站的电路功耗分别为PUE和PBS,则根据文献[5]可知系统消耗的总功率为

|
(3) |
其中η为功率放大器的效率.
当基站采用ZF检测算法时,即检测矩阵为

|
(4) |
由文献[3]可得基站接收到用户k的信噪比为
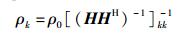
|
(5) |
其中[A]kk为矩阵A的第(k, k)个元素.根据随机矩阵知识可知,[(HHH)-1]kk-1是服从参数(N-K+1, 1) 的伽马分布[6].而由于lb(1+x-1)是凸函数,根据Jensen不等式,有E[lb(1+x-1)]≥lb(1+E-1[x]),故类似文献[3]中谱效的证明过程,系统谱效可近似表示为

|
(6) |
为了给出上行Massive MIMO系统采用ZF检测算法时能效和谱效、接收天线个数及小区半径间的权衡关系,进而给出系统的最优能效、相应的谱效和消耗的功率,本节首先讨论系统的平均功耗.
2.1 系统的平均功耗根据文献[7],当用户均匀分布在半径为R的小区内时,用户k与基站间距离dk的分布为

|
(7) |
其中r0为相对R非常小的距离.根据式(7) 有

|
(8) |
而根据对数正态分布的定义,可以得到

|
(9) |
因此,可以得到
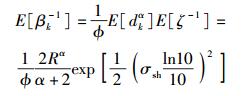
|
(10) |
为了行文方便,记β=E-1[βk-1].进而,可以得到系统消耗的平均总功率为

|
(11) |
根据能效的衡量尺度J/bit[1-4],可以得到小区长期的平均能效为
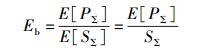
|
(12) |
进而可以得到下面能效和谱效间的关系.
定理1 当基站采用ZF检测算法时,上行massive MIMO系统的能效与谱效间关系表示为

|
(13) |
其中
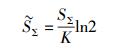
|
(14) |

|
(15) |

|
(16) |
证明 首先根据上行massive MIMO系统的谱效表达式(见式(6)),经过变形可以得到
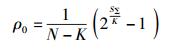
|
(17) |
而根据系统消耗的平均功率(见式(11)),可以得到ρ0的另一表达式为

|
(18) |
根据能效的定义(见式(12)),式(18) 可以写为
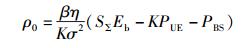
|
(19) |
令式(17) 等于式(19),可以得到

|
(20) |
化简式(20),可以得到能效和谱效间关系为

|
(21) |
记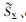
由定理1可得,增加基站接收天线个数可以增强系统能效,增加小区半径,弱化系统能效.而谱效对系统能效的影响将在2.3小节进一步探讨.
2.3 最优能效为了深入研究谱效对能效的影响,有必要建立如下的优化问题:

|
(22) |
利用凸优化知识可以得到如下的最优能效定理.
定理2 当上行massive MIMO系统采用ZF检测算法时,系统的最优能效可以表示为

|
(23) |
此时系统的谱效为

|
(24) |
系统消耗的平均总功率为

|
(25) |
其中:W0(·)为Lambert函数的第1个实分支,满足W0(x)eW0(x)=x,且W0:[-e-1, +∞)→[-1, +∞)[8].
证明 根据定理1可知,系统能效Eb是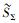

|
(26) |
进而,其二阶导数为

|
(27) |
根据凸函数的判别条件可知,函数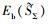


|
(28) |
根据Lambert函数的定义可以得到

|
(29) |
将式(14) 代入式(29),可以得到最优能效下的谱效为
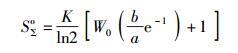
|
(30) |
将式(30) 代入式(13),可以得到系统的最优能效如式(23) 所示.
令式(30) 等于式(6),可以得到
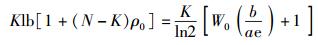
|
(31) |
式(31) 经过化简可得

|
(32) |
将式(32) 代入式(11),可以得到系统消耗的平均总功率,如式(25) 所示.
由定理2可以看出,系统的最优能效与基站的接收天线个数、复用的用户个数、电路功耗和功率放大器效率有关.增加接收天线个数可以增强系统最优能效,降低系统基带复杂度,减少系统电路功耗,有助于增强系统最优能效,提高功率放大器的效率和缩小小区半径.同样,可以增强系统的最优能效.
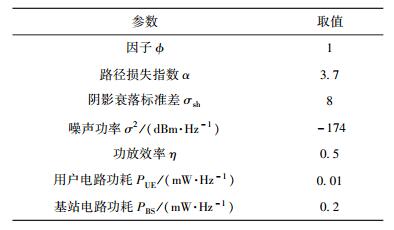
3 仿真结果与分析仿真中,天线个数根据文献[2-3]选取,大尺度参数和电路功率消耗主要根据文献[5]选取,如表 1所示.
|
|
表 1 上行massive MIMO系统参数 |
图 2给出了小区半径R=1km时系统能效与谱效间的关系.可以看出,当系统接收天线个数和用户数固定时,系统能效随着谱效的增加先降低后增加,而求得的最优能效的确在曲线的最低点处,证明了理论推导的正确性.同时表明,合理设置系统谱效工作点是提高系统能效的重要手段.此外,接收天线个数从100增加到500时,系统能效逐渐变好,表明增加天线个数可以增强系统能效.
|
图 2 能效与谱效间的关系(R=1km) |
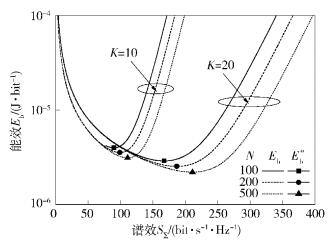
图 3给出了不同小区半径和用户数下,系统最优能效和接收天线数间的关系.固定小区半径和用户个数,随着基站接收天线数的增加,系统能效逐渐增强,与图 2的结论相同.而当小区半径从0.1km增加到1km时,系统能效逐渐弱化,表明微小区可以增强系统能效.当然,在天线阵列空间有限时,天线个数的增加破坏了信道独立性,会给性能带来一定损失,而小区半径减小将增加小区间干扰.考虑这些因素下的massive MIMO性能将是未来的研究方向.

|
图 3 最优能效与天线数及小区半径间的关系 |
为了研究上行Massive MIMO系统采用ZF检测算法时的能效问题,首先引进系统实际功耗模型,建立了能效与谱效、接收天线个数、用户个数和小区半径间的闭式关系,进而根据凸优化理论求得系统的最优能效.仿真结果表明,合理设置系统谱效工作点、增加基站接收天线个数和减少小区半径是增强系统能效的重要手段.
| [1] | Hasan Z, Boostanimehr H, Bhargava V K. Green cellular networks: a survey, some research issues and challenges[J]. IEEE Communication Survey & Tutorials, 2011, 13(4): 524–540. |
| [2] | Rusek F, Persson D, Lau E G, et al. Scaling up MIMO: opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40–60. doi: 10.1109/MSP.2011.2178495 |
| [3] | Ngo H, Larsson E, Marzetta T. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(4): 1436–1449. doi: 10.1109/TCOMM.2013.020413.110848 |
| [4] |
龙航, 旷婧华, 申山山, 等. 迫零中继系统中的空间信道配对与映射[J]. 北京邮电大学学报, 2010, 33(5): 84–88.
Long Hang, Kuang Jinghua, Shen Shanshan, et al. Spatial channel pairing and mapping in ZF relaying systems[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(5): 84–88. |
| [5] | He Chunlong, Sheng Bin, Zhu Pengcheng, et al. Energy efficiency and spectral efficiency tradeoff in downlink distributed antenna systems[J]. IEEE Wireless Communications Letters, 2012, 1(3): 153–156. doi: 10.1109/WCL.2012.022812.120048 |
| [6] | Couillet R, Debbah M. Random matrix methods for wireless communications[M]. New York: Cambridge University Press, 2011: 17-30. |
| [7] | Kim Y, Kwon T, Hong D. Area spectral efficiency of shared spectrum hierarchical cell structure networks[J]. IEEE Transaction on vehicular technology, 2010, 59(8): 4145–4151. doi: 10.1109/TVT.2010.2052938 |
| [8] | Corless R M, Gonnet G H, Hare D E G, et al. On the lambert wfunction[J]. Advances in Computational Mathematics, 1996, 5(4): 329–359. |
| [9] | Boyd S, Vandenberghe L. Convex optimization[M]. New York: Cambridge University Press, 2004: 100-101, 103. |