2. 中国联通研究院, 北京 100032
提出了一种下行多用户中继系统收发机联合优化算法,研究了基站端和中继端都采用预编码技术下基于最小均方误差准则的收发机联合优化问题.在第1跳信噪比较高的情况下,系统误差协方差矩阵可以简化分解为2个独立的部分,从而将两跳收发机联合优化问题的求解转化单跳多输入多输出(MIMO)优化问题进行求解,同时可以获得基站端预编码的闭式解,不仅简化了求解过程也降低了算法的计算复杂度和系统的信道信息反馈开销.仿真结果验证了算法的性能.
2. China Unicom Research Institute, Beijing 100032, China
A joint transceiver optimization is proposed for downlink multiuser multiple-input multiple-output (MIMO) relay systems. The proposed method is based on minimum mean-square error criterion. Using high signal-to-noise ratio approximation, the error covariance matrix is decomposed into two individual error matrices, which leads to two simple problems for the optimization, the simple traditional MIMO optimization and the traditional multiuser optimization. Moreover, the closed-form solution of the source precoding matrix can be obtained. The decomposition greatly degrades the complexity of the joint transceiver design and mitigates the feedback overhead. Simulations verify the effectiveness of the proposed method.
近年来,中继技术成为未来移动通信中一项非常重要的技术,得到了广泛的研究.而中继技术与MIMO系统的结合能进一步提高系统的容量和分集增益[1-2].为了最大限度地利用多天线中继系统的优势,需要进行合理的收发机设计. Oyman和Lzi等[3-4]进行了多用户中继系统的中继预编码矩阵的研究,但是并未考虑基站端预编码的联合设计,性能较差. Jang等[5]提出了一种基于最小均方误差(MSE, mean square error)准则的多用户中继系统中的联合收发机设计方法,该方法需要各节点已知两跳的信道信息,需要较大的信道信息的反馈开销.笔者提出了一种低复杂度低反馈开销的下行多用户中继系统中联合收发机设计,该方案通过对误差协方差矩阵进行分解,将联合优化的问题近似为2个相对独立的子问题:传统的点对点MIMO优化问题和传统的多用户MIMO问题.基于这种分解,推导得到基站预编码矩阵的闭式解,降低了系统实现的复杂度.并且算法实现中基站只需要知道第1跳的信道信息,用户接收端也只需要第2跳信道信息,降低了系统信道信息反馈开销.仿真结果表明,所提出的算法性能优于文献[3]中的算法,在计算复杂度和信道信息反馈量更低的情况下获得与文献[5]算法基本相同的性能.
1 下行多用户中继系统考虑下行多用户中继系统,系统中有1个基站,1个中继,K个用户,基站和中继各有Ns根天线和Nr根天线,用户k(k=1, 2,…, K)配置Nk根天线.接收天线总数为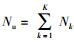

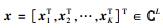
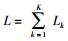
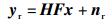
|
(1) |
其中: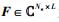
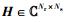

在第2个传输时隙,中继对接收到的信号进行预编码后发送给用户,第k个用户接收到的信号为

|
(2) |
其中:
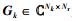
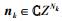
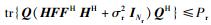
用户k利用线性接收矩阵
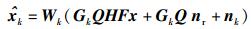
|
(3) |
因此,K个用户总的误差协方差矩阵可以表示为
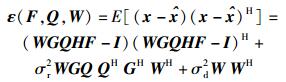
|
(4) |
其中: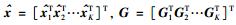
下行多用户中继系统中,基于最小MSE准则的联合收发机设计问题可以描述为
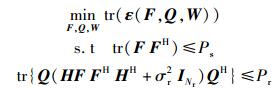
|
(5) |
上述问题不是关于F、Q、W的凸问题,不能直接用凸优化理论求解.本研究的求解思路是通过对总误差协方差矩阵进行分析和推导,将联合优化问题近似转换为2个独立传统的优化问题进行求解.
利用矩阵求逆定理,式(4) 可以表示为
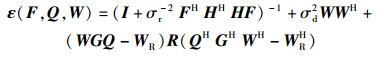
|
(6) |
其中:R=HFFHHH+σr2INr,WR=FHHHR-1.根据文献[5],中继处最优的预编码矩阵满足
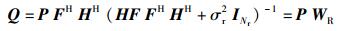
|
(7) |
即中继的预编码矩阵可以分解为一个前向线性预编码矩阵P和一个接收机WR的级联,因此对Q的优化可以转化为对P的优化.
将式(7) 代入式(6),得到

|
(8) |
其中

|
(9) |

|
当

|
即ε2只与矩阵W和矩阵P有关,而与基站端预编码F无关.而ε1只与F有关.则式(5) 可转化为2个相对独立的问题
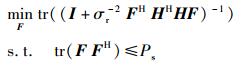
|
(10) |

|
(11) |
式(10) 等效于点对点MIMO系统的优化问题[6],而式(11) 与多用户MIMO优化问题[7]类似,式(11) 的目标函数可以理解为传统多用户MIMO系统中所有用户MSE的总和.因此式(5) 的求解转化为对式(10) 和(11) 的求解.
2.2 问题求解传统点对点MIMO优化问题(见式(10))最优解结构[6]为

|
(12) |
其中:V为H的右奇异矩阵,H=UΣ VH,Σ=diag{λ1, λ2, …, λNs}, Δf=diag{f1, f2, …, fNs}为功率矩阵,应用拉格朗日乘数法可得到Δf为
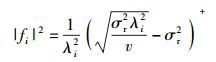
|
(13) |
其中(x)+=max (x, 0),v为引入的拉格朗日因子,v的值需要满足基站端的功率限制.
式(11) 可以看做一个基于MSE准则的多用户MIMO的收发机设计,P为下行多用户MIMO的发送预编码矩阵,W为用户接收矩阵.类似于文献[7],根据卡罗需-库恩-塔克条件[8],得到P和W.
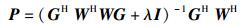
|
(14) |

|
(15) |
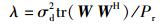
|
(16) |
其中P=[P1, P2, …, PK],Pk可以理解为用户k的预编码矩阵. P和W互为函数,因此可以采用如下的迭代算法对W和P进行求解.
1) 初始化:设W=IL×Nu,最大迭代次数为tmax;
2) 根据式(14) 和(16) 计算前向预编码矩阵P;
3) 判断如果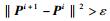
4) 根据更新后的P以及式(15) 更新用户接收均衡矩阵Wk;跳转2);
5) 归一化矩阵P以满足中继发送功率限制.
因为上述迭代算法在每次更新P和W时,式(11) 的目标函数都是单调递减的,并且问题(11) 的目标函数的是非负的,所以上述迭代算法能收敛.求解得到的得到P之后,再根据式(7),可计算得到中继预编码矩阵Q.
2.3 算法分析从上述求解的过程中可以看出,提出的算法可以获得基站预编码矩阵的闭式解,基站只需要知道第1跳的信道信息H.同时所提算法中用户k的接收均衡矩阵只与第2跳信道Gk有关.基站和用户只需要利用信道估计获得自己的本地等效信道信息就可以完成整个传输矩阵的设计.而文献[5]中算法的所有节点都需要同时知道H和Gk.因此,相比于文献[5]中算法,所提算法减少了用户反馈信道Gk给基站和中继反馈信道H给用户的信道反馈过程.
在计算复杂度方面,所提算法基站预编码矩阵具有闭式解.对中继预编码矩阵和用户接收矩阵间的迭代求解算法只在中继前向预编码矩阵和用户接收矩阵间进行.而文献[5]中的迭代算法涉及W、P、F,并且由于使用了上下行的对偶特性,迭代中的计算流程需要在上行与下行的处理矩阵之间来回进行.下面将对提出的算法和文献[5]中的算法进行复杂度分析.采用Flop数对复杂度进行度量.由于迭代过程占复杂度的主要部分,所以对算法单次迭代复杂度进行统计.所提出的算法复杂度和文献[5]中的算法计算复杂度分别如表 1和表 2所示.其中C表示对于式(14) 的计算复杂度.
|
|
表 1 提出的算法单次迭代复杂度 |
|
|
表 2 文献[5]中算法单次迭代复杂度 |
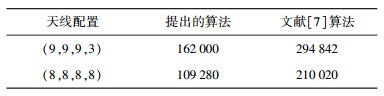
由于提出的算法中式(14) 与文献[5]中式(19) 均为类似的运算,在此近似地以相同的复杂度C来表示.由于C远小于其他运算的复杂度,在此忽略. 表 3给出了不同天线和用户发送数据流数配置下提出的算法与文献[5]中算法的Flop数量比较. (Ns, Nr, Nu, K)分别表示发射天线数、中继天线数、用户总天线数及用户数.这里假设L=Ns, Nk=Lk=Nu/K, k=1, 2, …,K.
|
|
表 3 提出的算法与文献[5]中算法的复杂度比较 |
从表 3可看出,提出算法的单次迭代复杂度相比于文献[5]减少近40%,即在相同的收敛特性情况下,提出算法的复杂度远小于文献[5]中的算法.仿真结果中将给出新算法和文献[5]中算法收敛性的比较.
3 仿真结果在仿真中,假设Ps=Pr,σr2=σd2=1.迭代算法的收敛门限为ε=10-4.信道样本为1万次.考虑3种方案进行比较.
1) 简单放大转发(AF, amplify and forward)方案

|
用户接收矩阵采用最小均方误差检测;
2) 基于最小均方误差(MMSE,minimum MSE)中继预编码方案[3]

|
3) 文献[5]方案.
图 1所示为提出的算法与文献[5]中算法在不同迭代次数下的误比特率(BER,bit error rate)性能.从图中可看出,该算法的收敛特性与文献[5]算法基本相同.根据上文单次迭代复杂度分析(见表 3)可以看出,在相同迭代次数的情况下,本算法的复杂度大大降低.

|
图 1 不同迭代次数下BER性能 |
图 2所示为提出的算法和上述3种方案在64QAM调制下的误比特率随基站和中继发射功率变化的曲线.假设有3个用户,每个用户配置3根天线,并且每个用户都发送3个数据流,基站和中继都配置9根天线,BER性能比较如图 2所示. 图 2显示,所提算法的BER性能要明显优于文献[3]中的AF和MMSE方案,因为提出的算法联合考虑收发的优化设计,而AF方案和MMSE方案都只单独考虑了中继的预编码.在所有信噪比范围内,该算法均实现了与文献[5]中算法几乎完全相同的BER性能.

|
图 2 BER性能比较 |
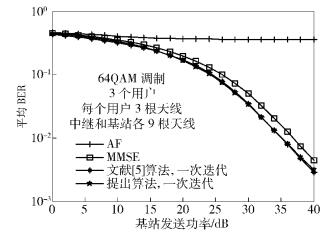
图 3给出了提出的算法在一次迭代时的BER性能比较.从图 3可以看出,所提的算法在迭代1次的情况下就能得到较好的性能,误比特率性能明显优于AF和文献[3]中的MMSE方案,并在计算复杂度和信道信息反馈开销大大下降的情况下获得与文献[5]在1次迭代时基本相同的性能.
|
图 3 一次迭代BER性能比较 |
对于下行多用户中继系统,提出一种联合收发机的设计方案,在高信噪比区域将误差协方差矩阵近似分解为2个独立的部分,将联合优化问题转化为一个传统的点对点的MIMO优化问题和一个传统的多用户MIMO问题进行求解.所提算法优化过程中,基站端可以获得基站预编码矩阵的闭式解,并且只需要知道第1跳的信道,且用户侧接收矩阵只需要知道第2跳的信道.所提算法具有较低的计算复杂度和信道信息反馈开销.仿真结果表明,在所有信噪比范围内,提出算法性能均优于AF方案和MMSE方案[3],并在计算复杂度和信道信息反馈开销大大下降的情况下,实现与文献[5]中算法几乎完全相同的BER性能.
| [1] | Tang Xiaojun, Hua Yinbo. Optimal design of non-regenerative MIMO wireless relays[J]. IEEE Transactions on Wireless Communication, 2007, 6(4): 1398–1407. doi: 10.1109/TWC.2007.348336 |
| [2] | Hua Y, Bliss D W, Gazor S, et al. Guest editorial: theories and methods for advanced wireless relays-issue Ⅱ[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(8): 1361–1367. doi: 10.1109/JSAC.2013.130801 |
| [3] | Oyman O, Paulraj A J. Design and analysis of linear distributed MIMO relaying algorithms[J]. IEE Proceedings Communications, 2006, 153(4): 565–572. doi: 10.1049/ip-com:20050406 |
| [4] | Lzi Y A, Falahati A. Amplify-forward relaying for multiple-antenna multiple relay networks under individual power constraint at each relay[J]. EURASIP Journal on Wireless Communications and Networking, 2012(50): 1–10. |
| [5] | Jang S, Yang J, Kim D K. Minimum MSE design for multiuser MIMO relay[J]. IEEE Communications Letters, 2010, 14(9): 812–814. doi: 10.1109/LCOMM.2010.072610.100583 |
| [6] | Palomar D P, Cioffi J M, Lagunas M A. Joint Tx-Rx beamforming design for multicarrier MIMO channels: a unified framework for convex optimization[J]. IEEE Trans on Signal Process, 2003, 51(9): 2381–2401. doi: 10.1109/TSP.2003.815393 |
| [7] | Xu Daofeng, Yang Luxi, He Zhenya. Linear transceiver design for multi-user MIMO downlink[J]. Electronic Letters, 2008, 44(22): 1310–1311. doi: 10.1049/el:20081062 |
| [8] | Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004. |