为了将全球定位系统(GPS)和基站定位系统相结合,以实现城市环境中的无缝定位及更高的定位精度,提出了一种针对GPS/基站定位系统的信息融合算法.通过分析接收机运动特点,建立系统状态模型,采用联邦卡尔曼滤波器,对2个定位系统的定位信息进行先分散后集中处理.分析了信息分配因子对滤波效果的影响,并提出了一种根据精度因子及载噪比来进行信息分配的方法.该算法通过融合GPS和基站的定位数据,可有效提高定位精度.仿真及实测结果说明了算法的有效性.
An information fusion algorithm was proposed for using both global positioning system (GPS)/base-station positioning system to get high positioning accuracy. The system state was modeled by analyzing the movement features, and the federated Kalman filter was used to fuse the two systems. The effect of information distribution factor was analyzed. A distribution method was proposed by horizontal dilution of precision and carrier to noise ratio. The positioning accuracy was improved by using the proposed algorithm. Simulations and examinations show the effectiveness of the algorithm.
近年来,GPS得到越来越广泛的应用.但GPS有着信号弱、易受干扰等缺点,在城市峡谷、楼宇内部等遮挡、干扰较为严重的区域很难正常工作,定位精度会严重下降甚至无法定位[1-2].基于移动数据通信网的TC-OFDM(time&code division-orthogonal frequency division multiplexing)定位系统,利用通信基站在OFDM信号体制上融合了高精度定位信号,可实现定位信号的广域覆盖,不仅能有效补充GPS信号盲点,甚至可覆盖GPS信号无法达到的室内、隧道等区域.
将GPS与基站进行融合定位,可以有效提高定位覆盖区域和定位精度,是一种实现室内外高精度无缝定位的有效手段.提出了一种基于联邦卡尔曼的GPS /基站定位信息融合算法.该算法先通过局部卡尔曼滤波器分别对GPS、基站子系统进行局部最优估计;再利用全局滤波器,通过一定的权值分配策略,将各子滤波器结果进行融合,得到最优融合结果.仿真及实测结果说明了算法的有效性.
1 GPS/基站组合导航系统GPS /基站组合导航系统的上行站将基于现有OFDM体制的节目信号与授时信号上行至卫星;卫星将节目信号与授时信号播发至地面广播基站,由卫星授时接收机对广播基站进行高精度时间同步;广播基站将高精度定位信号融合到OFDM信号上,形成高同步精度的TC-OFDM定位信号;终端同时接收多颗GPS卫星信号及多个基站的定位信号,将二者的定位信息进行融合,得到高精度定位结果.
2 定位信息融合模型 2.1 系统运动模型在二维空间中,系统的状态变量为[3]
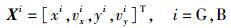
|
(1) |
其中:G、B分别为GPS子系统和基站子系统,x、y分别为东向及北向位置,vx、vy分别为东向及北向速度.状态方程为
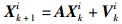
|
(2) |
其中:A为状态转移矩阵;V为过程噪声,符合均值为零,标准差为σvi的高斯分布,并记Q为V的协方差矩阵;下标k表示更新历元.以T表示定位信息更新周期,则

|
(3) |
联邦卡尔曼滤波模型由2个子卡尔曼滤波器和1个全局主滤波器构成. GPS与基站子滤波器分别对GPS和基站测得的定位信息进行局部卡尔曼最优估计,得到XG和XB,同时得到估计误差协方差矩阵PG和PB;主滤波器将局部最优估计与主滤波器状态信息XM、PM进行融合,得到全局最优估计X和全局估计误差P;主滤波器将X和P反馈给各子滤波器,同时利用信息分配因子βG和βB分别对GPS及基站子滤波器进行加权.
3 定位信息融合算法 3.1 信息融合流程信息融合最初是指对来自不同传感器的测量信息进行优化融合处理[4].可分别将GPS与基站的定位信息视为不同传感器的测量值,二者的测量方程为
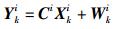
|
(4) |
其中:C为系统测量矩阵,由于GPS与基站子系统均能测得位置及速度,所以C为单位矩阵;W为测量噪声,符合均值为零,标准差为σwi的高斯分布,并记R为W的协方差矩阵.在子滤波器中利用测量值中带来的新息对一步预测值进行修正,得到局部最优估计为
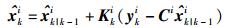
|
(5) |
其中K为卡尔曼增益.采用融合—反馈模式联邦卡尔曼滤波器[5],将各子滤波器的局部最优估计送入主滤波器,按式(6) 进行信息融合,得到全局最优融合.
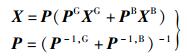
|
(6) |
主滤波器中不进行测量,只进行时间更新,因此将主滤波器的过程信息按照式(7) 所示的分配准则与子滤波器进行信息分配.
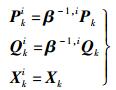
|
(7) |
其中信息分配因子β满足信息守恒定理:
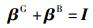
|
(8) |
其中I为单位矩阵.
3.2 信息分配方法信息分配因子在联邦卡尔曼中起十分重要的作用,它完成了全局滤波估计对局部滤波估计的加权:
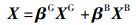
|
(9) |
由式(9) 和式(6) 可得
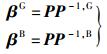
|
(10) |
由式(10) 可以看出,若对系统i的估计误差Pi越大,则相应的βi越小;反之越大.说明系统i越不精确,它对滤波结果的影响越小.事实上,估计误差反映了系统对最终状态的估计精度,当某一系统的测量噪声过大,测量结果不准时,应动态调整测量误差协方差矩阵R,“通知”滤波器做出适当调整,以减小P,从而保持最优滤波.但实际系统中实时得到测量误差协方差的精确值是不现实的,联邦卡尔曼滤波是在不改变R的情况下,通过改变β来达到间接改变各子系统估计误差的目的,从而达到全局最优滤波的.
图 1对上述情况进行了仿真.以一维情况为例,接收机以5 m/s的速度做匀速直线运动.前200个测量历元中,GPS和基站系统的测量值分别满足σxG =3 m、σxB =5 m的高斯分布,记为场景1;后200个测量历元中,由于GPS丢星或受到干扰等原因,导致测量噪声变为σxG =10 m的高斯噪声,记为场景2.滤波器初始噪声协方差矩阵满足场景1的噪声统计特性;信息分配因子初始值满足βG : βB =(σxB )2: (σxG )2,即βG =0.69、βB =0.31.
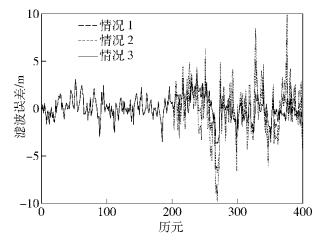
|
图 1 信息分配因子的影响 |
图 1中的3条曲线分别表示以下3种情况下的全局估计:① 滤波器参数未做任何改变(长虚线);② 场景2中,信息分配因子变为βG =0.2、βB =0.8,但测量噪声协方差不变(短虚线);③ 场景2中,测量噪声协方差根据场景2的噪声特性做出相应更改,而信息分配因子不变(实线).
由图 1可以看出,实线的滤波效果最好,说明获得噪声统计特性是得到最优滤波估计最有效的途径,但是实际情况中实时获得噪声统计特性却是不现实的;短虚线的滤波效果次优,说明通过更改信息分配权重,即使不了解噪声统计特性,也可以达到较好的滤波效果;长虚线的滤波效果最差,说明滤波器在不做任何调整的情况下无法达到最优滤波.
注意到图 1中短虚线的信息分配因子是根据场景2的噪声统计特性得出的,这仍不适用于实际情况,因此,需要通过其他途径估计2个子系统的信息分配权重.可以利用式(11) 来表征GPS水平定位精度:

|
(11) |
其中:h为水平精度因子,它只与接收机和卫星的相对位置有关;σρ为伪距测量误差,它与载噪比CN0之间符合SIGMA -ε模型[6],即
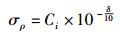
|
(12) |
其中:δ表示载噪比,Ci为方差比例因子.构造满足以下条件的函数:
1) 以h及δ为自变量,β为因变量;
2) 定义域∈(0, +∞),值域∈[0, 1];
3) 关于各自变量的偏导数单调不增/减;
4) 在定义域上连续可导.
为了构造上述函数,可先构造βG关于h的函数:

|
(13) |
其中X1、X2为阈值,且有0 < X1 < X2.当h<X1时认为GPS足够精确,只利用GPS定位信息;而h>X2时认为GPS已失效,只利用基站定位信息.信息分配曲线如图 2所示,曲线在(X1, X2)内随h单调递减,说明随GPS精度下降,GPS子系统在联邦卡尔曼滤波器中的作用减小,基站子系统作用加大.
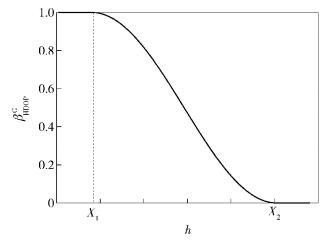
|
图 2 关于HDOP的信息分配曲线 |
同理构造βG关于δ的函数:
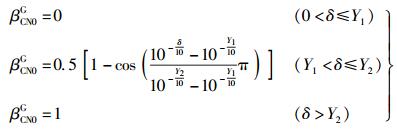
|
(14) |
其中Y1、Y2为阈值,且有0 < Y1 < Y2.这里δ越大,信号质量越好,因此βCN0G是单调增函数.由式(13) 和式(14) 可得βG关于h及δ的二元函数为
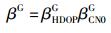
|
(15) |
利用信息守恒定理可求出βB的表达式.在实际应用中,不能出现β为零的情况,否则会导致滤波发散,这时只需将β置为较小值即可.
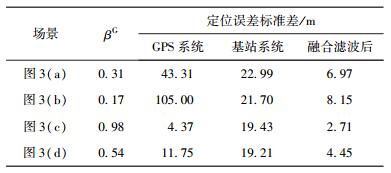
4 仿真结果假设接收机以2 m/s的速度进行匀速直线运动,基站定位系统的定位误差符合均值为0,标准差为20 m的高斯分布,GPS系统的δ有35 dB·Hz和45 dB·Hz两种情况,h有2.0和5.0两种情况.取X1=1.5,X2=8.0,Y1=33 dB·Hz,Y2=50 dB·Hz,则4种情况下的滤波结果如图 3所示.
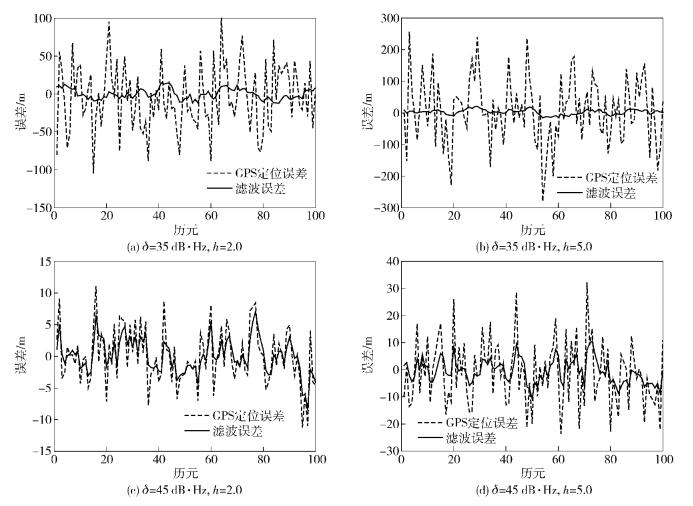
|
图 3 滤波效果对比 |
从图 3中可以看出,CN0对GPS定位误差影响较大,HDOP影响相对较小. 4种情况下的滤波误差都小于GPS单系统定位误差. 表 1列出了4种情况下的误差标准差和信息分配因子对比,当GPS系统CN0较大且HDOP较小时,GPS系统的定位误差较小,其信息分配因子较大. 4种情况下滤波误差标准差均小于任一系统的定位误差标准差.在图 3(a)及图 3(b)场景中,虽然GPS定位误差很大,但滤波误差没有受到过多影响,仅有小幅增加.综上可以说明,所提出的联邦卡尔曼滤波算法有较好的滤波效果.
|
|
表 1 测试结果对比 |
2011年,在北京邮电大学校园内建立了基于移动数据通信网的TC-OFDM定位系统.实验网中包括4个定位基站,它们可提供精度优于10 ns的时间同步,并覆盖校园内大部分区域. 图 4中标出了位于学三楼及教三楼的2个基站,另外2个基站分别位于学三基站东侧(学29基站)及教三基站东南侧(明光楼基站).通过北京邮电大学自主研发的定位接收机同时利用GPS和基站系统进行定位,并对定位信息利用所提出的算法进行数据融合,得到的定位结果如图 4所示.
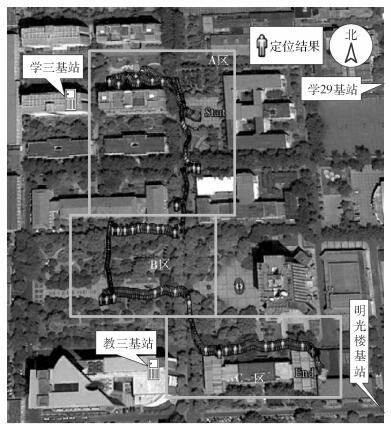
|
图 4 实测定位结果 |
实验路径大致可分为3个区域.
1) A区.周围楼房较为密集,在行走过程中,GPS卫星时隐时现,且载噪比波动较大. A区北部误差较大,这里处于高楼之间,卫星被严重遮挡,又处于基站定位系统的覆盖边缘,几何精度较差,因此融合误差也较大.但基站与GPS的融合保证了定位结果的连续性,且误差仍优于独立GPS系统.随着南行,A区GPS可见星逐渐增多并趋于稳定,同时进入基站覆盖区,定位精度明显提高.
2) B区.周围较空旷,卫星信号理想,GPS权重比较大,融合定位结果精度很高.
3) C区.南面被遮挡严重,GPS可见星数减少,但此处基站定位信号良好,且几何精度较高,融合后的定位结果也较为精确.结束部分处于宽约5 m的楼房夹缝中,卫星几乎被全部遮挡,GPS失效,但从图 4中可看出仍有较高的定位精度,说明在信号和几何分布良好时,基站定位系统也有较高的定位精度.
6 结束语根据GPS和基站定位系统的特点,提出了一种基于联邦卡尔曼滤波器的定位信息融合算法.通过信息融合,提高了系统的定位精度及定位鲁棒性.通过分析信息分配权重对滤波结果带来的影响,提出了基于HDOP及CN0的信息分配方法.通过仿真验证了算法的有效性.利用基于移动数据通信网的TC-OFDM定位实验网,测试了实际应用效果.仿真及测试结果表明,GPS /基站定位系统可以实现高精度室外无缝定位.
| [1] |
滕云龙, 师奕兵, 郑植. 恶劣环境下GPS接收机定位算法研究[J]. 仪器仪表学报, 2011, 32(8): 1879–1884.
Teng Yunlong, Shi Yibing, Zheng Zhi. Research on GPS receiver positioning algorithm under bad conditions[J]. Chinese Journal of Scientific Instrument, 2011, 32(8): 1879–1884. |
| [2] | Alexandre V P, Nel S. Interference mitigation in a repeater and pseudolite indoor positioning system[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(5): 810–820. doi: 10.1109/JSTSP.2009.2027805 |
| [3] | Deng Zhongliang, Yin Lu, Yang Lei. Virtual noise and variable dimension Kalman filter for maneuvering target tracking[C]//Advanced Technology in Teaching-Proceedings of the 2009 3rd International Conference on Teaching and Computational Science (WTCS 2009). Shenzhen: Springer Press, 2012: 909-917. |
| [4] |
万树平. 基于熵权的多传感器目标识别方法[J]. 系统工程与电子技术, 2009, 31(3): 500–510.
Wan Shuping. Multi-sensor target recognition based on entropy weight[J]. Systems Engineering and Electronics, 2009, 31(3): 500–510. |
| [5] |
付梦印, 邓志红, 张继伟.
Kalman滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 2003: 167-169.
Fu Mengyin, Deng Zhihong, Zhang Jiwei. Kalman filtering theory and its application in navigation system[M]. Beijing: Science Press, 2003: 167-169. |
| [6] | Brunner F K, Hartinger H, Troyer L. GPS signal diffraction modelling: the stochastic SIGMA-Δ model[J]. Journal of Geodesy, 1999, 73(5): 259–267. doi: 10.1007/s001900050242 |