2. 咸阳师范学院数学与信息科学学院, 陕西 咸阳 712000
基于整数环Zn上圆锥曲线的多重签名思想,提出了一种高效的整数环Zn上圆锥曲线的多重签密方案.在基于大整数分解和圆锥曲线离散对数的双重困难问题下对方案的安全性进行了证明.该方案中的签密和解签密运算是在圆锥曲线上进行的,因此明文嵌入方便,求逆简单,元素阶的计算及曲线上点的运算均更加容易.与现有方案的效率进行对比,提出的多重签密方案在信息运算量方面有极大的改进.
2. Mathematics and Information Science College, Xianyang Normal University, Shanxi Xianyang 712000, China
A scheme for efficient multiple signcryption on the conic curve over the ring Zn is presented based on multiple digital signature. The security of the proposed scheme is proved based on the two hard problems of large integer factorization and discrete logarithm on conic curve. As the signcryption and de-signcryption are calculated on conic curve, plaintexts can be embedded easily, and in inverse, the element order and points' operation on conic curve over can be calculated more simply and easily in the proposed scheme. Compared with the exiting scheme in efficiency, the proposed scheme is greatly improved in information computation.
为了在网络信息传输中同时满足机密性和认证性,Zheng[1]在1997年首次提出了基于有限域上的签密方案,将签名和加密相结合的同时保证了机密性、认证性、不可伪造性.显然,签密方案相对于传统“先签名后加密”的方法而言,在计算时间和存储空间上的代价都有所降低.所以签密体制的设计引起了研究者的极大兴趣[2-9].多重签密是指多个发送者对同一消息进行签密,并使多重签密数据长度大致与单独的签密数据相同,从而在完成对多个发送者认证的同时,大大降低数据的传输量.基于以上原因,许多密码学研究者对多重签密的工作原理进行了深入研究,设计出了许多高效且安全的签密方案[6-8].现有的一些方案多数是利用椭圆曲线构造双线性形成的,虽然保证了方案的安全性,但信息运算量较大.所以提高签密的运算效率是一个重要的研究课题.肖龙等[9]提出了一个整数环Zn上的圆锥曲线数字签名及多重签名方案,并说明在大整数分解和离散对数双重困难问题下方案是安全的.
根据圆锥曲线上的多重签名思想,提出一个基于整数环Zn上的圆锥曲线的多重签密方案.该方案由签密、组合数据、解签密及验证4个部分构成.经过分析,在基于大整数分解和圆锥曲线离散对数双重困难问题下,该方案具有更好的安全性和抗破解性.与文献[7]进行比较,提出的方案在签密和解签密阶段的运算效率方面都具有很好的优势,降低了信息运算量.
1 整数环Zn上的圆锥曲线Cn(a, b)的群结构设n是一个正整数,Zn是一个模n的剩余类环.定义环Zn上的圆锥曲线Cn(a, b)是同余方程y2=ax2-bx(mod n)在Zn上的解集[10].其中,n=pq,p、q是2个不同的奇素数. (a, n)=(b, n)=1,a、b∈ Zn.文献[10]证明了环Zn上的圆锥曲线(Cn(a, b), ⊕)构成一个有限加法交换群,并且给出了曲线上所有有理点的坐标表示和运算法则.
定理 1 [10] 设n=pq,其中p、q是2个不同的大素数,满足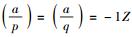
文献[11]指出Cn(a, b)总存在着阶为Nn的基点,并且给出了计算基点的方法.
相比椭圆曲线,圆锥曲线是具有以下性质的代数曲线:明文嵌入容易,同时也易于从曲线中恢复出明文、曲线群的阶容易计算、点易于求逆等.研究结果表明[12],由于圆锥曲线明文嵌入容易,点的运算简单,如果利用标准二进制来表示,则更能节约近1/4的运算量,并被证明无法再改进.所以,在圆锥曲线上建立密码体制和签名体制比在有限域上更具有吸引力.
2 Cn(a, b)上的多重签密方案 2.1 系统参数设置选择一条密码学上的圆锥曲线Cn(a, b),其中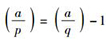
公开:n, a, b, G, H, H1, H2;保密:p, q, Nn.
2.2 密钥提取算法该算法由密钥中心(PKG,public key generation)执行.输入系统参数和身份D∈{0, 1}*,算法步骤为:假设有n个签密者Ui,用户Ui的身份为Di∈{0, 1}*,计算KDi=H(Di)且(KDi, Nn)=1, KDiLDi≡1(mod Nn),Si=LDiG(mod n),每个签密者的公钥私钥对为(KDi, Si);相应的接收者B的身份为DB∈{0, 1}*,则其密钥对为(KDB, SB).再选择一个对称密码算法的加密、解密算法EK()、DK().
2.3 签密算法用户Ui对待签密消息m∈{0, 1}*的签密过程如下:
1) 每个签密者随机选择一个正整数ki∈ Z N\{0},计算Ci=kiG(mod n),若Ci=0,则重新选择整数ki.
2) 每个签密者计算δi=Ci+SiH(m).若(δi-Ci)KDi=0(mod n),则重新选择ki.
3) 每个签密者将数据信息(Ci, δi)发送给聚合者(签密者之一).聚合者收到(Si, Ci, δi)后,验证
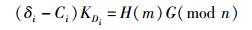
|
是否成立.若成立,则计算C=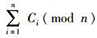
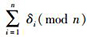
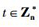
接收者收到密文(δ, C, U, V, r)后,解密f=tKDB利用自己的私钥SB计算m=V+H2(fSB(mod n)).
2.5 验证算法接收者利用聚合者的公钥K′检验
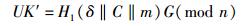
|
是否成立?若成立,则接收该密文;否则,拒绝.
3 方案分析由签密算法过程可以看出,本方案的安全性是基于大整数分解的困难性和圆锥曲线上的离散对数困难问题.每个成员利用选择的随机数ki和自己的私钥Si对消息m进行加密,所以基于大数分解和离散对数双重困难问题下,任何第三方无法对不合法的消息进行合法的签密或者恢复出明文消息.
该方案也可以抵抗小解密指数攻击.文献[10]指出,圆锥曲线上的RSA加密方案可以抵抗低加密指数攻击和低解密指数攻击,因而比有限域上的RSA方案更安全.
Wiener[13]提出了一种攻击方案,利用有限简单连分数展式可有效地求出解密私钥,有如下定理.
定理 2 Wiener定理:设n=pq, (n, c)表示一个RSA用户的公开信息,c是加密指数,d是私钥指数,如果素数p、q满足q < p < 2q且1 < d < 4 n /3,则通过(n, e)可有效地求出d.
王标等[11]将该性质继承到曲线Cn(a, b)上,给出了定理3.
定理 3 设n=pq, (n, K, a, b)表示Cn(a, b)上的公开信息,K″是签名指数,L″是验证指数,若素数p、q满足q < p < 2q且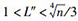
所以在选择合适的K使得L满足定理3的条件下,该方案能够抵抗小解密指数攻击.可见,该方案具有更强的安全性和抗破解性.
4 方案效率分析如果记Pm表示圆锥曲线上点的数乘运算,Ad表示圆锥曲线上点加运算,Iv表示环Z Nn\{0}上求逆运算,I′ v为乘群上的求逆运算,P′ m表示乘群上的乘法运算,E表示对运算,e′表示指数运算,h表示哈希运算,忽略数的乘法运算量及bit或运算量,那么与文献[7]的签密方案进行比较,信息计算量比较如表 1所示.
|
|
表 1 运算效率比较 |
由表 1可见,虽然在信息聚合过程中聚合者的运算量较大,但是在其他过程所需要的运算量却非常少,所以如果将总的运算量加在一起,本方案在运算量上明显优于文献[7]所提方案,此外,由于圆锥曲线上的点乘运算和椭圆曲线上的点乘运算相比计算量要小得多[14],如果利用标准二进制表示,则计算量能节约近1/4.所以提出的多重签密方案具有更优的运算效率.
5 结束语利用正整数环Zn上圆锥曲线的公钥密码体制和签名算法,提出了一种基于双重困难问题的多重签密方案.分析结果表明,在基于大整数分解和曲线上离散对数双重困难问题下,签密方案具有更强的安全性和抗破解性.此外,由于圆锥曲线具有明文嵌入简单、点的计算量小等特点,所以与文献[7]的方案相比,提出的方案运算更加简单,运算效率更高,实用性更强.
| [1] | Zheng Yuliang. Digital signcryption or how to achieve cost (signature & encryption) cost(signature)+cost(encryption) [C]//Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology. Berlin: Spring, 1997: 165-179. |
| [2] |
庞辽军, 崔静静, 李慧贤, 等. 新的基于身份的多接收者匿名签密方案[J]. 计算机学报, 2011, 34(11): 2014–2113.
Pang Liaojun, Cui Jingjing, Li Huixian, et al. A new multi-receiver ID-based anonymous signcryption[J]. Chinese Journal of Computer, 2011, 34(11): 2014–2113. |
| [3] |
刘文琦, 顾宏, 杨建华. 基于身份的同时生效签密体制研究[J]. 电子与信息学报, 2011, 33(7): 1582–1588.
Liu Wenqi, Gu Hong, Yang Jianhua. Identity-based concurrent signcryption scheme[J]. Journal of Electronics and Information Technology, 2011, 33(7): 1582–1588. |
| [4] |
刘连东, 冀会芳, 韩文报, 等. 一种无随机预言机的无证书广义签密方案[J]. 软件学报, 2012, 23(2): 394–410.
Liu Liandong, Ji Huifang, Han Wenbao, et al. Certificate less generalized signcryption scheme without random oracles[J]. Journal of Software, 2012, 23(2): 394–410. |
| [5] |
赵秀凤, 徐秋亮. 一个有效的多PKG环境下基于身份签密方案[J]. 计算机学报, 2012, 35(4): 673–681.
Zhao Xiufeng, Xu Qiuliang. An efficient multi-PKG ID-based signcryption scheme[J]. Chinese Journal of Computer, 2012, 35(4): 673–681. |
| [6] | Zhang Bo, Xu Qiuliang. Identity-based multisigncryption scheme without random oracles[J]. Chinese Journal of Computers, 2010, 33(1): 103–110. doi: 10.3724/SP.J.1016.2010.00103 |
| [7] |
张秋璞, 叶顶锋. 对一个基于身份的多重签密方案的分析与改进[J]. 电子学报, 2011, 39(12): 2714–2720.
Zhang Qiupu, Ye Dingfeng. Cryptanalysis and improvement of an identity-based multi signcryption scheme[J]. Acta Electronica Sinica, 2011, 39(12): 2714–2720. |
| [8] | Yap W S, Heng S H, Goi B M. On the security of an identity-based aggregate signature scheme[C]//The 22nd International Conference on Advanced Information Networking and Applications-Workshops, AINAW 2008. Okinawa: IEEE Press, 2008: 1523-1528. |
| [9] |
肖龙, 王标, 孙琦. 基于环Zn上圆锥曲线数字签名和多重数字签名[J]. 西安交通大学学报, 2006, 40(6): 648–718.
Xiao Long, Wang Biao, Sun Qi. Digital signature and multiple digital signatures based on the conic curve over Zn[J]. Journal of Xi'an Jiao Tong University, 2006, 40(6): 648–718. |
| [10] |
孙琦, 朱文余, 王标. 环Zn上圆锥曲线和公钥密码协议[J]. 四川大学学报:自然科学版, 2005, 42(3): 471–478.
Sun Qi, Zhu Wenyu, Wang Biao. The conic curve over Zn and public-key cryptosystem protocol[J]. Journal of Sichuan University: Natural Science Edition, 2005, 42(3): 471–478. |
| [11] |
王标, 方颖珏, 林宏刚, 等. 基于环Zn上圆锥曲线的QV签名方案[J]. 中国科学, 2009, 39(2): 212–217.
Wang Biao, Fang Yingjue, Liu Honggang, et al. QV signature protocol on conic curve over ring Zn[J]. Science in China, 2009, 39(2): 212–217. |
| [12] | Dai Zongduo, Pei Dingyi, Yang Junhui, et al. Cryptanalysis of a public key cryptosystem based on conic curves [C]//The International Workshop on Cryptographic Techniques and E-Commerce. Hong Kong:, 1999: 259-261. |
| [13] | Wiener M J. Cryptanalysis of short RSA secret exponents[J]. IEEE Trans Inf Theory, 1990, 36(3): 553–558. doi: 10.1109/18.54902 |
| [14] | Li Hangyu. The scalar multiplication of points on a conic over finite fields[J]. Information Security and Communications Privacy, 2007(8): 64–69. |



