阿尔茨海默病(Alzheimer's disease,AD)是典型的慢性神经退行性疾病之一,会随着患者认知能力的下降而影响其正常生活[1, 2].静息态功能磁共振成像(resting state-functional magnetic resonance imaging,rs-fMRI)已成为探索脑功能网络的重要工具.目前,大多用于rs-fMRI数据的分析方法都假设在成像过程中脑功能连接(functional connectivity,FC)是恒定的,该假设有可能忽略神经系统疾病导致的脑部功能连通性的变化[3].针对上述问题,有研究[4, 5]提出了基于rs-fMRI的动态功能连接(dynamic functional connectivity,dFC)分析方法.dFC可以揭示静态功能连接(static functional connectivity,sFC)分析方法无法显示的脑网络的快速波动和时变特征.dFC方法构建脑网络的一种常用技术是滑动窗口技术[6].采用滑动窗口技术可以观察到特定时间点或时间窗口间的波动性,更能体现大脑的时变特性.
目前AD领域的研究主要是对sFC结合图论指标进行分析[7],dFC在AD研究领域的应用还不多. Schumacher等[8]研究了AD、路易氏体痴呆(dementia with Lewy bodies,DLB)患者与正常对照(normal controls,NC)组的动态脑网络差异性,主要对图论指标中全局效率和本地效率进行了分析;de Vos等[9]采用图论指标中的连接度和聚类系数作为特征进行了AD的分类研究.这些dFC在AD领域的研究均采用基于图论的分析方法,在单尺度上对大脑网络进行过滤,存在尺度值及阈值选择的问题.而基于持久同调的分析方法研究动态脑网络可在多尺度上对大脑网络进行过滤,避免了尺度值及阈值选择的问题,而且该方法已经在静态脑网络中表现出良好的应用效果[10, 11].持久同调是拓扑数据分析的一个重要研究方向,核心思想是研究多过滤尺度的拓扑结构,分析其各个维度下贝蒂数(Betti numbers plot,BNP)β0、β1和β2的变化,在过滤尺度的变化过程中,持续时间较短的拓扑特征为噪声,持续时间较长的特征用来表示其内在特性.它已经广泛应用于三维模型检索[12]、复杂网络以及脑影像学分析[9, 10]等领域.在脑网络研究中,本课题组[10]提出将基于持久同调的集成持久特征(integrated persistent feature,IPF)作为一种新的拓扑属性,并使用其斜率(the slope of IPF plot,SIP)作为单变量特征来衡量静态脑网络的多尺度过滤过程.相对于传统的图论方法,它更能体现大脑的动力学过程,而且避免了传统方法单一尺度值或阈值选择的问题.但是IPF将脑区和脑区之间FC作为边权,结合最小生成树对脑网络进行全部尺度的过滤,完成了多尺度的量化,其更多考虑的是用平均时间序列来研究空间尺度的拓扑特性.然而FC的强度在几秒到几分钟时间范围内都会发生很大变化,所以将时间信息通过滑动窗加入到持久同调的研究对于探索脑网络动力学时空特性至关重要,该研究可能探寻到基于磁共振图像的AD患者脑功能网络的潜在生物标志物.
本文的主要研究内容如下:
(1) 构建静态脑功能网络,以及基于滑动窗口的动态功能脑网络,对构建后的全脑和默认模式网络(default mode network,DMN)子网的图论指标与持久同调指标进行统计检验.
(2) 采用k均值聚类对AD患者和NC被试的滑动窗口进行聚类,分析AD患者和NC被试dFC的时间属性.
1 数据与方法 1.1 数据来源本研究所使用的rs-fMRI数据集来源于ADNI(Alzheimer’s disease neuroimaging initiative)-2公开数据集(http://adni.loni.usc.edu),我们选择了在年龄、受教育年限、性别以及头部运动等方面都没有显著性差异的被试参与本次研究,剔除预处理不符合要求的个体后,共对68例被试(包括31例AD和37例NC)进行了分析.68例被试的脑影像数据均为利用3.0 T飞利浦MRI扫描仪,采用回波平面成像(Echo Planar Imaging,EPI)序列获得的高分辨率的rs-fMRI三维影像数据.扫描参数如下:回波时间(echo time,TE)=30 ms,切片厚度=3.3 mm,切片数=48,矩阵大小=64×64,翻转角=80˚,重复时间(repetition time,TR)=3 000 ms,时间点个数(volume)=140.表 1为被试者的人口统计学特征的详细信息.
| 表 1 被试者的人口统计学特征 Table 1 Demographic characteristics of the subjects |
使用SPM12 (http://www.fil.ion.ucl.ac.uk/spm/)[13]和DPARSF工具箱[14]进行rs-fMRI数据的预处理.主要包含:
(1) 丢弃每个被试的rs-fMRI数据前10个时间点,以获得信噪比较高和稳定的信号.剩下的130个时间点用于进一步分析.
(2) 针对扫描层之间的差异,进行切片的时间层校正.将TR/2时间点的切片作为参考扫描层,其他扫描层向其对齐,以保证每个切片的数据对应相同的时间点.
(3) 针对每个被试的结构图像(T1图像),将其功能数据标准化到MNI(Montreal neurological institute)空间,以进行空间校正.
(4) 依次对图像使用4 mm半高宽的高斯核进行空间平滑,去除信号中的线性趋势,对带通滤波(0.01~0.08 Hz)进行了数据处理.
(5) 对时间序列进行协变量回归分析,消除由脑脊液、白质信号及刚体变换六个头动参数(三个方向的平移,三个轴向的旋转)引起的信号波动.
由于目前研究对是否消除全脑信号还有争议[15],因此本研究未对全脑信号进行回归.
1.3 脑网络构建对预处理后的数据使用自动解剖标记模板(anatomical automatic labeling 90,AAL90)将大脑划分为90个脑区(不包括小脑)[16-18],使用每个区域内所有体素的平均来获得每个脑区的时间序列.考虑到采用的无向加权网络,因此采用皮尔逊(Pearson)相关系数来计算FC.
1.3.1 传统静态脑网络的构建将90个脑区作为网络节点,计算每对脑区在130个时序信号下的Pearson相关系数,作为网络边的定义,从而为每例被试构建一个90×90的Pearson相关矩阵,如(1)式所示.
| $ r = \frac{{\sum\nolimits_{i = 1}^n {({x_i} - \bar x)} ({y_i} - \bar y)}}{{\sqrt {\sum\nolimits_{i = 1}^n ( {x_i} - \bar x{)^2}\sum\nolimits_{i = 1}^n ( {y_i} - \bar y{)^2}} }} $ | (1) |
其中n为时间点个数(本文n=130),r为x脑区与y脑区之间的Pearson相关性.xi表示第i个时间点第x个脑区的平均时间序列,yi表示第i个时间点第y个脑区的平均时间序列.
由于做Fisher z变换需要Pearson相关矩阵满足正态分布,而该矩阵是否服从正态分布目前还有不同见解[8, 19, 20],有些研究[10, 19, 20]并未对Pearson相关矩阵作Fisher z变换,本文也采用这种方式.脑网络构建之后对该矩阵的图论指标和持久同调指标进行双样本t检验.
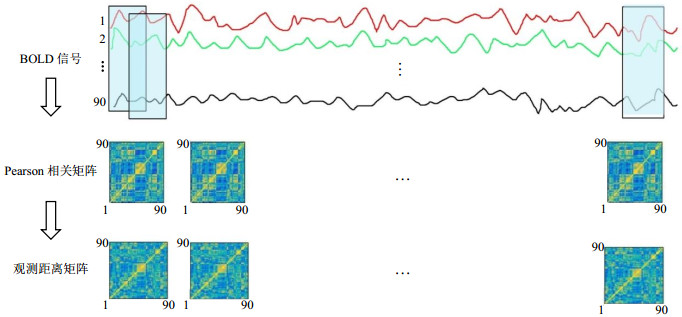
1.3.2 基于滑动窗口的动态脑网络的构建本研究使用Matlab(R2016b),对基于Pearson相关的观测距离矩阵进行动态脑网络构建(以全脑为例).使用滑动窗口方法计算每个窗口90个脑区之间的Pearson相关性.具体而言,使用滑动窗口(长度=20 TR=60 s)与高斯核(σ=3 TR)[6, 21]进行卷积来创建锥形窗口.锥形窗口的优点是减少了子序列窗口滑动时边界时间点的权重.每个窗口的起始位置与上一个窗口的起始位置以1个TR的步长逐渐滑动,从而形成111(130-20+1)个窗口,在每个时间窗内计算了每对脑区之间的Pearson相关,并计算得到观测距离矩阵.之所以选择60 s的窗口长度,是因为先前的研究[22]表明30~60 s的窗口长度可能会在FNC估计的质量和时间特性之间进行良好的折衷.之后为每个被试生成了时变Pearson相关矩阵(111个90×90),这些相关矩阵可以捕捉静止状态扫描期间FC的动态变化,并用作进一步分析FC状态和时间变异性研究的输入.
构建动态脑网络的具体细节如下(令时间序列长度为L,滑窗窗口长度为W,
a) 滑动窗口的构建:对于90个脑区长度为L的时间序列,提取出K个子序列,
算法选择:本研究采用的血氧水平依赖(blood oxygen level-dependent,BOLD)fMRI信号为连续变量,针对脑区间的FC进行分析,因此采用基于Pearson相关的方法来计算边权.对于产生的第k个子序列(
b) 对每个Pearson相关矩阵取绝对值后通过(2)式计算观测距离矩阵.
| $ {W_x}\left( {{x_i}, {x_j}} \right) = 1 - corr\left( {{x_i}, {x_j}} \right) $ | (2) |
c) 每个被试构建
图 1为构造观测距离矩阵的步骤:
|
图 1 使用滑动窗口构建观测距离矩阵 Fig. 1 Estimating observed distance matrix using sliding windows |
为了探索脑网络动力学可变性,本文从脑网络FC的时间变异性的角度进一步研究了组间差异.将时间变异性定义为对每个被试所有窗口的观测距离矩阵阈值过滤后取标准偏差形成一个标准差矩阵,来定量估计随时间变化的FC的稳定性,然后结合动态网络分析(包括动态图论指标和持久同调指标)与k均值聚类来计算AD患者和NC被试脑网络动力学时空特性的差异性.
1.4 脑网络FC分析 1.4.1 图论指标图论分析方法已被广泛应用于静态脑网络的研究[7].本文主要比较了目前广泛使用的图论指标:全局效率、本地效率、特征路径长度、向量中心度、聚类系数、小世界属性、网络半径指标,用以计算网络全局及部分传输能力(全局效率,本地效率)、脑区之间的最短路径(特征路径长度)、节点的重要程度(向量中心度)、节点的集聚程度(聚类系数)、小世界网络特性以及整个网络水平的度量(网络半径)等.这些图论指标通常是在单尺度上对脑网络进行度量,在对其计算之前需对脑网络构建得到的观测距离矩阵进行过滤.统计分析是常用的过滤阈值方法,它首先删除观测距离矩阵中无显著连接的边(p﹥0.05)以获得较稀疏的网络结构[7, 23],然后对过滤后的矩阵取标准偏差计算图论指标,最后再对结果进行双样本t检验.本文图论指标的计算都是采用脑连接工具BCT(brain connectivity toolbox)[24]实现的.
1.4.2 持久同调指标持久同调是一个新兴的数学概念.基于BNP的持久性特征被认为是一种有用的特征描述符.BNP[25]可以在图过滤过程中区分持久存在的特性和噪声.在一些神经退行性疾病中,BNP已成功地应用于基于氟脱氧葡萄糖正电子发射断层扫描(fluorodeoxyglucose positron emission tomography,FDG-PET)[19, 20]和T1加权磁共振成像数据[20]的脑网络研究.本文使用的0维贝蒂数(
| $ {\beta _0}(T, {\lambda _i}) = m - i, \;\;\;\;0≤i≤m - 1 $ | (3) |
其中m为最大连通分支数,
IPF定义如(4)式所示:
| $ IP{F_\lambda } = \left\{ \begin{array}{l} \frac{{m - i}}{{m(m - 1)}}\sum\limits_{k = i + 1}^{m - 1} {{\lambda _k}} , \;\;\;0≤i≤m - 2\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = m - 1n \end{array} \right. $ | (4) |
其中
由于IPF值是一条单调递减的收敛函数,因此IPF的斜率的绝对值(SIP)可以作为一个脑网络多尺度研究的量化指标;而且医学领域倾向于使用单一指标,所以本文也选取SIP作为单一的持久同调衡量指标.本文中持久同调指标的计算都是基于Matlab实现的.
基于持久同调的属性描述的是多尺度空间信息,将其与脑网络动力学中的时间信息相结合,将为脑网络的演化研究提供一种新思路.
1.4.3 动态FC状态的时间属性本研究首先使用k均值聚类捕捉动态时间序列的FC状态变化,进而对所有AD患者和NC被试中动态FC重复出现的状态进行组间差异性分析.
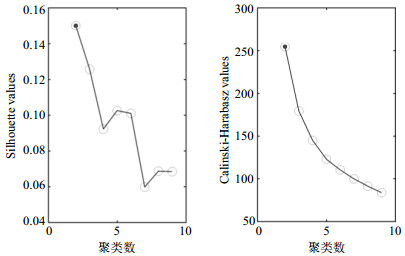
k均值聚类方法通过迭代的方式,使用距离函数把数据集聚成不同的簇,簇内相似性很高,簇间相似性极低.具体为将k均值算法根据其曼哈顿距离(L1距离)应用于Pearson相关矩阵.为了确定k值(即聚类数,本文将k值设定为2~9),本文对每个k值重复k均值过程100次.使用Silhouette得分和Calinski-Harabasz指数评估聚类结果的有效性.Silhouette得分和Calinski-Harabasz指数标准都显示2为最合适的聚类数(k=2),聚类数的选择如图 2所示(实心点为最佳聚类数).为每种状态的所有窗口计算一个特定FC矩阵(聚类中心),矩阵中的每个元素都是所有窗口矩阵中属于一个状态的相应元素的中值.
|
图 2 最优聚类数(k值)的选择 Fig. 2 Optimization for the number of clusters (k values) |
针对每种状态,本文从两个方面量化了AD和NC组间动态FC状态时间属性的差异,包括窗口比例的分布(即停留在每个状态窗口的比例)和每个状态的平均停留时间(即在一个状态上的连续窗口数).本文利用DynamicBC工具箱进行了上述聚类分析[26].
1.4.4 统计检验对静态脑网络和动态脑网络的图论指标、持久同调指标以及动态FC状态聚类分析的时间属性进行双样本t检验,p<0.05表示两组的差异具有统计学意义.本文使用Matlab(R2016b)进行统计检验.
2 实验结果与讨论 2.1 全脑(AAL90)FC分析AD患者的脑FC研究中,全脑FC分析能够反映全脑网络的功能耦合程度,可以从全局角度把握脑网络各个感兴趣区域(region of interest,ROI)之间的FC状态,对于AD的病理研究具有深刻的意义.
2.1.1 全脑网络连接指标分析本研究首先基于静态和动态全脑网络对AD患者和NC被试的图论指标和持久同调指标进行了分析(表 2为双样本t检验对应的p值),结果显示,基于静态脑网络的图论指标中网络半径属性在AD患者和NC被试间表现出显著差异(AD患者平均值±标准差:6.17±2.63;NC被试平均值±标准差:5.97±2.64,p=0.049 3<0.05);全局效率属性虽然在静态脑网络中组间差异更大,但是组间也没有显著差异(p﹥0.05).说明图论指标在动态全脑网络研究中并没有显著优于静态全脑网络.静态脑网络持久同调指标中,SIP属性在组间表现出非常显著差异(AD:-0.67±0.13;NC:-0.75±0.10,p=0.007 7<0.01)、BNP属性在两组被试组间也有显著差异(AD:-257.16±43.18;NC:-283.12±56.82,p=0.040 7<0.05);然而基于动态脑网络分析结果显示,BNP在AD和NC的组间差异更显著(AD:-718.53±84.92;NC:-793.13±109.96),p值显著低于静态脑网络(p=0.003 0<0.01,远小于0.040 7);而SIP属性的表示组间差异性(AD:-0.52±0.11;NC:-0.59±0.09)的p值也低于静态脑网络(p=0.001 7<0.007 7).但是无论是基于静态全脑网络还是动态全脑网络,持久同调指标在AD和NC的组间差异性均明显大于图论指标;所以基于持久同调的动态脑网络分析更有可能探寻到潜在的生物标记物.
| 表 2 基于静态全脑网络和动态全脑网络,AD患者与NC被试间的图论指标和持久同调指标分析 Table 2 Characteristics analysis based on graph theory and persistent homology between AD and NC with static whole brain network and dynamic whole brain network |
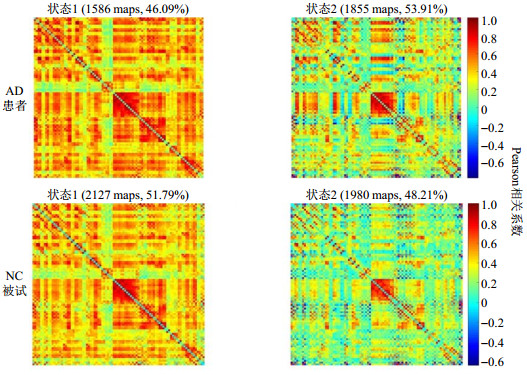
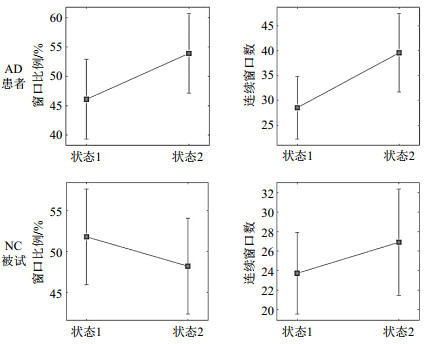
为了验证AD患者与NC对照的脑网络FC的时间属性是否存在差异.本文对AD组和NC组所有被试全部窗口的Pearson相关矩阵进行聚类分析,将AD和NC被试窗口分别聚类为两个簇(状态1和状态2,相对而言,状态1是强连接状态,状态2是弱连接状态),并从窗口比例分布和平均停留时间两个方面量化了动态全脑网络FC状态时间属性的差异.窗口比例分布以百分比表示(即图 3中每种状态对应的百分比),阐述了停留在每个状态窗口的比例,maps对应为状态内窗口数.平均停留时间表示属于一个状态的连续窗口数,该时间是通过将从一个状态更改为另一种状态之前的连续窗口数进行平均而得出的(图 4).
|
图 3 AD患者和NC被试的动态全脑网络的聚类中心图 Fig. 3 Cluster center diagram based on the dynamic whole brain network of AD patients and normal controls |
|
图 4 AD患者和NC被试的动态全脑网络的状态窗口比例和连续窗口数 Fig. 4 Window percentage rate distribution and average numbers of window stayed based on the dynamic whole brain network of AD patients and normal controls |
从图 3和图 4可知相对于NC被试,AD患者在强连接状态(状态1)的窗口比例减少了约5.70%,而在弱连接状态(状态2)的比例相应增加;而且在状态2的连续窗口数相对较多[AD:(40±8)个窗口;NC:(27±5)个窗口,p<0.05].这表明AD患者的脑网络FC更倾向于停留在弱连接状态.
2.2 DMN子网网络连接分析DMN是AD研究中广泛研究的功能子网络,集中了AD产生认知障碍的相关脑区,持久同调相关方法虽然在静态脑网络中效果显著[10, 11],但是在DMN动态脑网络中的研究还是未知.作为AD患者变异性最明显的的功能子网络之一,其时变网络的研究在神经病理学方面有着重要的意义.AAL90脑模板中DMN的划分[27]如表 3所示.
| 表 3 AAL90脑模板中默认模式网络(DMN)的划分[27] Table 3 The division of the default mode network in (DMN) the AAL90 brain template[27] |
在静态网络分析中,DMN的FC在AD患者中发生了变化[27],但是关于DMN子网的动态FC研究依然有限.基于全脑FC的研究,本文首先使用滑动窗口方法为每个被试的26个脑区计算动态DMN,每个滑动时间窗都会求得一个观测距离矩阵,对每个被试的观测距离矩阵阈值过滤后跨越所有窗口求标准偏差,然后对其进行图论指标和持久同调指标分析,并使用双样本t检验比较了AD组和NC组指标是否表现出差异性(p<0.05),结果如表 4所示.
| 表 4 基于静态DMN网络和动态DMN网络,AD患者与NC被试间的图论指标和持久同调指标分析 Table 4 Characteristics analysis based on graph theory and persistent homology between AD and NC with static DMN network and dynamic DMN network |
由表 4可知在静态DMN网络图论指标中,向量中心度在两组间具有非常显著差异性(AD:0.104 6 ±0.01;NC:0.104 7±0.01,p<0.01),在动态网络中也有差异(AD:0.194 6±0.01;NC:0.195 0±0.01,p<0.05),而这个指标在全脑研究中并没有差异,表明了DMN网络相对于全脑更能显示AD与NC的差异性.全局效率基于静态DMN网络时在两组间的差异大于动态网络,但是这种差异也没有显著性;静态DMN网络中小世界属性在两组间没有显著差异(p﹥0.05),但是在动态DMN网络中在两组被试中显示出了非常显著的差异(AD:1.03±0.02;NC:1.02±0.01,p<0.01),说明小世界属性在动态DMN网络中能够显示出细微的时间变异性差异.动态DMN子网FC分析中,双样本t检验结果显示SIP(AD:-0.69±0.12;NC:-1.46±0.10,p=0.003 3)与BNP(AD:-171.41±32.24;NC:-198.84±34.08,p=0.001 2)在AD和NC组间均具有显著差异性;而在静态脑网络中,SIP(AD:-0.67±0.13;NC:-0.75±0.10,p=0.004 0)组间具有显著差异,BNP(p﹥0.05)无显著差异.但是无论是基于动态DMN子网还是静态DMN子网,相对于图论指标,基于持久同调的指标均更能将AD和NC区分开来,所以基于持久同调的动态DMN子网分析更有可能探寻到AD成像的潜在生物标志物.
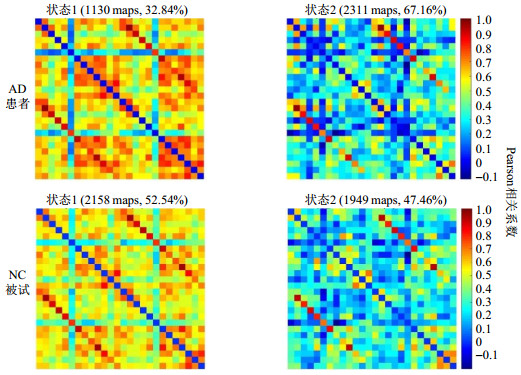
2.2.2 动态DMN子网聚类分析DMN子网的聚类分析与全脑网络类似,每种状态窗口的比例以百分比表示(图 5).平均停留时间表示某组参与者属于一个状态的连续窗口数(图 6).由图 5和图 6可知,聚类结果包含了两个高度结构化的FC状态,这两个状态在整个个体扫描期间以及跨被试窗口之间重复出现.DMN子网的聚类分析结果与全脑网络表现相似,且AD与NC组间差异更加显著.相对于NC被试,AD患者在强连接状态(状态1)窗口比例减少了19.70%,在弱连接状态(状态2)相应增加了19.70%.图 6中AD患者在状态2的窗口比例(AD:67.16%±5.58%;NC:47.46%±5.52%,p<0.05)明显较高,AD在状态2的连续窗口数也相对较多(AD:(47±8)个窗口;NC:(28±6)个窗口,p<0.05),说明AD患者的DMN脑网络FC更倾向于弱连接状态.
|
图 5 AD患者和NC被试的动态DMN子网的聚类中心图 Fig. 5 Cluster center diagram based on the dynamic DMN network of AD patients and normal controls |

|
图 6 AD患者和NC被试的DMN子网的状态窗口比例和连续窗口数 Fig. 6 Window percentage rates distribution and average numbers of window stayed based on dynamic DMN network of AD patients and normal controls |
本研究的创新之处在于:将持久同调的多尺度空间信息与滑动窗口的时间信息相结合,研究了脑网络的时间演化和空间演化,这将为AD相关的脑网络生物标志物的研究提供新见解,也可以为其他动态脑网络群体差异性,以及脑网络分类性研究[2, 28]提供新思路.本研究的不足之处在于:首先,本文未对纵向数据以及ApoE数据进行验证.其次,虽然本文虽然较好诠释了功能脑网络的时空信息,而且得到了较好的实验结果,但是本文未与行为学数据进行相关性分析.
3 结论本文研究了AD患者与NC被试在脑网络动力学和动态脑网络时空特性方面的差异,得到如下几点结论:(1)滑动窗口与持久同调相结合的方法在动态脑网络中的表现强于图论属性;(2)聚类结果显示,AD更倾向于弱连接状态,但是聚类的状态分析t检验结果也没有优于基于持久同调的分析方法;(3)相对于全脑研究,动态DMN网络更能显示出AD时间变异性差异.总之,AD患者动态脑网络所包含的时间演化信息以及基于持久同调的的FC所包含的多尺度空间演化信息的结合,为AD脑网络演化的研究提供了新的见解.
致谢 感谢"山西省自然科学基金资助项目(201901D111150)"对本研究的支持
利益冲突 无
| [1] | PIEVANI M, HAAN W D, WU T, et al. Functional network disruption in the degenerative dementias[J]. The Lancet Neurology, 2011, 10(9): 829-843. DOI: 10.1016/S1474-4422(11)70158-2. |
| [2] |
SUN J W, YAN S J, HAN Y S, et al. Classifying the course of Alzheimer's disease with brain MR images and a method based on three-dimensional local pattern transformation[J].
Chinese J Magn Reson, 2019, 36(3): 268-277.
孙京文, 闫士举, 韩勇森, 等. 基于脑部磁共振图像三维局部模式变换特征提取进行阿尔茨海默病病程预测分类[J]. 波谱学杂志, 2019, 36(3): 268-277. |
| [3] | HUTCHISON R M, WOMELSDORF T, ALLEN E A, et al. Dynamic functional connectivity: promise, issues, and interpretations[J]. Neuroimage, 2013, 80: 360-378. DOI: 10.1016/j.neuroimage.2013.05.079. |
| [4] | CALHOUN V D, ADALI T. Time-varying brain connectivity in fMRI data: whole-brain data-driven approaches for capturing and characterizing dynamic states[J]. IEEE Signal Proc Mag, 2016, 33(3): 52-66. DOI: 10.1109/MSP.2015.2478915. |
| [5] | PRETI M G, BOLTON T A W, VAN DE VILLE D. The dynamic functional connectome: State-of-the-art and perspectives[J]. Neuroimage, 2017, 160: 41-54. DOI: 10.1016/j.neuroimage.2016.12.061. |
| [6] | SHEN K, HUTCHISON R M, BEZGIN G, et al. Network structure shapes spontaneous functional connectivity dynamics[J]. J Neurosci, 2015, 35(14): 5579-5588. DOI: 10.1523/JNEUROSCI.4903-14.2015. |
| [7] | WANG J H, ZUO X N, DAI Z J, et al. Disrupted functional brain connectome in individuals at risk for Alzheimer's disease[J]. Biol Psychia, 2013, 73(5): 472-481. DOI: 10.1016/j.biopsych.2012.03.026. |
| [8] | SCHUMACHER J, PERAZA L R, FIRBANK M, et al. Dynamic functional connectivity changes in dementia with Lewy bodies and Alzheimer's disease[J]. NeuroImage Clin, 2019, 22: 101812. DOI: 10.1016/j.nicl.2019.101812. |
| [9] | DE VOS F, KOINI M, SCHOUTEN T M, et al. A comprehensive analysis of resting state fMRI measures to classify individual patients with Alzheimer's disease[J]. Neuroimage, 2017, 167: 62-72. |
| [10] | KUANG L Q, HAN X, CHEN K W, et al. A concise and persistent feature to study brain resting-state network dynamics: Findings from the Alzheimer's Disease Neuroimaging Initiative[J]. Hum Brain Mapp, 2019, 40(4): 1062-1081. DOI: 10.1002/hbm.24383. |
| [11] | 况立群. 持久同调与共形映射下三维点云的特征表示研究[D]. 太原: 中北大学, 2018. |
| [12] |
KUANG L Q, LI L, XING J C, et al. 3D model retrieval method based on persistent homology[J].
Computer Engineering and Design, 2020, 41(6): 1773-1778.
况立群, 李丽, 幸嘉诚, 等. 基于持久同调的三维模型检索方法[J]. 计算机工程与设计, 2020, 41(6): 1773-1778. |
| [13] | PENNY W D, FRISTON K J, ASHBURNER J T, et al. Statistical parametric mapping: the analysis of functional brain images[M]. Elsevier: 2011. |
| [14] | YAN C G, ZANG Y F. DPARSF: a MATLAB toolbox for "pipeline" data analysis of resting-state fMRI[J]. Front Syst Neurosci, 2010, 4: 13. |
| [15] | FOX M D, ZHANG D, SNYDER A Z, et al. The global signal and observed anticorrelated resting state brain networks[J]. J Neurophysiol, 2009, 101(6): 3270-3283. DOI: 10.1152/jn.90777.2008. |
| [16] | ZHUO Z Z, MO X, MA X Y, et al. Identifying aMCI with functional connectivity network characteristics based on subtle AAL atlas[J]. Brain Res, 2018, 1696: 81-90. DOI: 10.1016/j.brainres.2018.04.042. |
| [17] | KHAZAEE A, EBRAHIMZADEH A, BABAJANI-FEREMI A. Application of pattern recognition and graph theoretical approaches to analysis of brain network in Alzheimer' s disease[J]. J Med Imag Health In, 2015, 5(6): 1145-1155. |
| [18] | TZOURIO-MAZOYER N, LANDEAU B, PAPATHANASSIOU D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J]. Neuroimage, 2002, 15(1): 273-289. DOI: 10.1006/nimg.2001.0978. |
| [19] | CHOI H, KIM Y K, KANG H, et al. Abnormal metabolic connectivity in the pilocarpine-induced epilepsy rat model: a multiscale network analysis based on persistent homology[J]. Neuroimage, 2014, 99: 226-236. DOI: 10.1016/j.neuroimage.2014.05.039. |
| [20] | LEE H, KANG H, CHUNG M K, et al. Integrated multimodal network approach to PET and MRI based on multidimensional persistent homology[J]. Hum Brain Mapp, 2017, 38(3): 1387-1402. DOI: 10.1002/hbm.23461. |
| [21] | WANG J J, WANG Y, HUANG H Y, et al. Abnormal intrinsic brain functional network dynamics in unmedicated depressed bipolar Ⅱ disorder[J]. J Affect Disorders, 2019, 253: 402-409. DOI: 10.1016/j.jad.2019.04.103. |
| [22] | PRETI M G, BOLTON T A W, VAN DE VILLE D. The dynamic functional connectome: State-of-the-art and perspectives[J]. Neuroimage, 2017, 160: 41-54. DOI: 10.1016/j.neuroimage.2016.12.061. |
| [23] | SMITH S M, NICHOLS T E. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference[J]. Neuroimage, 2009, 44(1): 83-98. DOI: 10.1016/j.neuroimage.2008.03.061. |
| [24] | RUBINOV M, SPORNS O. Complex network measures of brain connectivity: uses and interpretations[J]. Neuroimage, 2010, 52(3): 1059-1069. DOI: 10.1016/j.neuroimage.2009.10.003. |
| [25] | CHUNG M K, HANSON J L, YE J P, et al. Persistent homology in sparse regression and its application to brain morphometry[J]. IEEE T Med Imaging, 2015, 34(9): 1928-1939. DOI: 10.1109/TMI.2015.2416271. |
| [26] | LIAO W, WU G R, XU Q, et al. DynamicBC: a MATLAB toolbox for dynamic brain connectome analysis[J]. Brain Connect, 2014, 4(10): 780-790. DOI: 10.1089/brain.2014.0253. |
| [27] | KUANG L Q, JIA J Y, ZHAO D Y, et al. Default mode network analysis of APOE genotype in cognitively unimpaired subjects based on persistent homology[J]. Front Aging Neurosci, 2020, 12: 188. DOI: 10.3389/fnagi.2020.00188. |
| [28] |
LIU K W, LIU Z L, WANG X Y, et al. Prostate cancer diagnosis based on cascaded convolutional neural networks[J].
Chinese J Magn Reson, 2020, 37(2): 152-161.
刘可文, 刘紫龙, 汪香玉, 等. 基于级联卷积神经网络的前列腺磁共振图像分类[J]. 波谱学杂志, 2020, 37(2): 152-161. |
 2021, Vol. 38
2021, Vol. 38 
