2. 厦门理工学院 光电与通信工程学院, 福建 厦门 361024;
3. 波谱与原子分子物理国家重点实验室, 武汉磁共振中心(中国科学院 武汉物理与数学研究所), 湖北 武汉 430071;
4. 厦门大学 电子科学系, 福建省等离子体与磁共振重点实验室, 福建 厦门 361005
2. School of Opto-Electronic and Communication Engineering, Xiamen University of Technology, Xiamen 361024, China;
3. State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, National Center for Magnetic Resonance in Wuhan(Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences), Wuhan 430071, China;
4. Department of Electronic Science, Xiamen University, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen 361005, China
核磁共振(Nuclear Magnetic Resonance,NMR)波谱是利用NMR现象检测物质的成分和结构的强有力工具,在生物[1]、化学[2]和医学[3]等领域应用广泛.比如,NMR波谱可用于分析化合物基团[4]、解析蛋白质结构[5-8]、无创伤探测活体组织物理化学特性[3]等.随着检测对象的越发复杂,传统的1D NMR波谱由于容易造成谱峰拥挤,在化合物识别和定量分析方面便有所不足.多维NMR波谱(维度≥2)能更好地表示相同或不同原子核(比如氢、碳、氧等)之间的耦合关系[9],可以提供比1D NMR波谱更加丰富的信息,广泛用于研究复杂的生物分子.此外,一些特殊的多维谱还能提供额外信息.比如,扩散排序谱(Diffusion-Ordered NMR SpectroscopY,DOSY)的扩散系数维可通过估计扩散系数来分析混合物特性,并应用于药物筛选[10]等.可见,多维NMR波谱在物质结构分析中发挥着重要作用.
采样时间长是多维NMR面临的主要挑战之一,NMR波谱的采集时间随着分辨率和维度的增加而迅速增长,2D谱到4D谱的全采样时间从分钟上升至几十天[9].非均匀采样(Non-Uniformly Sampling,NUS)是通过降低采集数据量来实现NMR快速采样的典型方法之一[11-16].但是,由于NUS采集的数据量低于奈奎斯特采样准则,谱峰存在明显伪峰,因而需要引入合适的信号模型来重建NMR波谱[11-16].
在过去的20多年里,研究者陆续提出了一系列有效地从NUS数据中重建出高质量NMR波谱的方法(图 1).早在1984年,最大熵方法(Maximum Entropy,MaxEnt)被引入NMR信号处理[17],该方法在满足采样到的数据约束下,从可能的解中选择熵最大的作为重建的完整谱,能够有效的减少采样伪峰[9],但噪声较强时容易产生谱峰失真[18].1988年,CLEAN方法采用启发式的迭代重建,在迭代中确定最大峰再进行去卷积,然后从源信号减去后再确定下一个次高峰再去卷积,以此类推直到给定残差水平[18].之后,研究人员结合随机同心壳采样大大提高该方法的欠采样和去伪谱峰能力[19]. 2001年,多维分解方法(MultiDimensional Decomposition,MDD)被引入波谱重建,其数学模型假设是N(N > 2)维张量分解为少数张量的和,每个张量中只有一个或者少量几个谱峰[9, 20].2007年,压缩感知(Compressed Sensing,CS)方法首次应用于二维NMR谱的欠采样重建,其假定在小波变换域内谱是稀疏的[21].但2010年第18届国际医学磁共振大会摘要中指出NMR谱具有自稀疏特性,并从稀疏性和相干性的角度分析认为小波变换不适合NMR谱重建,建议最小化波谱Lp(0 < p≤1)范数进行稀疏谱重建[11].2011年,利用同样的自稀疏特性,研究人员将CS应用于蛋白质NMR快速采集[13].2015年,研究人员提出NMR时域信号的低秩(Low-Rank,LR)重建方法[15]:该方法首先将NUS数据转化为数据缺失的Hankel矩阵,然后通过低秩矩阵恢复得到完整频谱.2016年,多维稀疏迭代峰型增强(Sparse Multidimensional Iterative Lineshape-Enhanced,SMILE)算法利用NMR谱的已知相位和时域信号的指数衰减特性重建2D到4D的NMR数据[22].该方法能够有效处理大数据集,并且可用于扩展常规的均匀采样数据.2019年,深度学习(Deep Learning,DL)方法采用密集卷积神经网络去除NUS引入的频谱伪影,然后进一步精炼中间重构的频谱以保持数据与采样数据一致性.随着不断地重建,伪影逐渐被去除,最终产生完整的频谱[16, 23].该方法能实现毫秒到秒超快速重建,具有很好的鲁棒性。在给定的NUS密度和波谱维数下对网络进行一次训练,然后将其用于不同样品的不同光谱.只要数据集具有相同的维数(2D或3D),并且波谱点数和NUS级别的差异不大,就不需要对不同的样本和频谱类型的网络进行重新训练[16].

|
图 1 磁共振谱重建方法发展的时间轴 Fig. 1 Development timeline of NMR spectrum reconstruction methods |
最近几年,研究人员主要利用NMR波谱的数学性质进行谱图重建.NMR波谱的数学性质主要包括稀疏性[11-14, 24-26]和低秩性[15],前者假定NMR波谱中非零值很少[11-14],后者假定谱峰个数很少[15]. 稀疏重建在频域实施,该方法假定谱峰(非零值)所占频率范围远低于观测频率范围,即NMR波谱在频域是稀疏的,然后通过最小化谱的L1(或L0)范数来进行谱图重建[11-14],它也称为CS-NMR方法.低秩重建主要是在时域实施,该方法假定谱峰个数很少,先将时域信号,也称自由感应衰减(Free Induction Decay,FID)信号,转化为Hankel矩阵,然后利用Hankel矩阵的秩(谱峰个数)远小于矩阵维度这一低秩数学特性,通过核范数最小化重建FID,最后进行傅里叶变换得到完整波谱.与稀疏重建相比,低秩重建可以同时适用于满足稀疏特性的窄谱峰和无法满足稀疏特性的宽谱峰,从而提高重建波谱的有效灵敏度,在理论上被认为是最适合NMR谱图重建的方法[27].
本文主要综述了近五年来基于低秩矩阵的NMR波谱重建方法的发展.首先介绍低秩矩阵的相关数学基础;然后从一般低秩矩阵和结构化低秩Hankel矩阵两个角度来论述重建模型,并讨论相关的数值算法及其NMR应用;最后分析了该技术存在的不足,并展望其未来发展的趋势.
1 相关数学背景 1.1 稀疏性稀疏信号指绝大多数元素为0的信号.从数学角度来看,对于一个长度为N的信号
R阶子式:设A为
矩阵的秩:在矩阵A中存在一个不等于0的R阶子式,且所有
如果矩阵之间各行的相关性很强,就表示这个矩阵可以投影到更低维的线性子空间,即用几个向量就能完全表达整个矩阵,则该矩阵是低秩的[29].一般认为
核范数(Nuclear Norm)是指矩阵奇异值的和,矩阵A的核范数用
对于低秩矩阵
| $\mathop {\min }\limits_{\bf{X}} rank({\bf{X}}), {\rm{ s}}{\rm{.t}}.{\rm{ }}{P_\Omega }({\bf{M}}) = {P_\Omega }({\bf{X}})$ | (1) |
其中,
秩最小化问题是一个非凸的优化问题,直接求解比较困难.而解决这一问题的常用方法是采用核范数最小化代替秩最小化,于是得到凸优化问题[30, 31]:
| $\mathop {\min }\limits_{\bf{X}} {\left\| {\bf{X}} \right\|_{\rm{*}}}, {\rm{ s}}{\rm{.t}}{\rm{. }}{P_\Omega }({\bf{M}}) = {P_\Omega }({\bf{X}})$ | (2) |
低秩Hankel矩阵(Low Rank Hankel Matrix,LRHM)方法将FID建模成有限个指数函数叠加,先把FID转化为Hankel矩阵,再利用Hankel矩阵的低秩性进行重建,即Hankel的秩远小于矩阵维度(远小于是指两者之间至少相差一个数量级以上).它主要分为四个步骤[5, 6, 15, 32]:(1)获取NMR信号的欠采样数据;(2)构建欠采样FID的低秩Hankel矩阵重建模型;(3)用数值算法求解FID;(4)将重建的完整FID经傅里叶变换后得到完整的NMR谱图.
2.1.1 指数函数与低秩Hankel矩阵LRHM方法基于FID信号可以建模成复指数函数叠加的形式,即:
| ${y_m} = \sum\limits_{j = 1}^J {({A_j}{{\rm{e}}^{{\rm{i}}{\phi _j}}}){{\rm{e}}^{ - \frac{{m\Delta t}}{{{\tau _j}}}}}{{\rm{e}}^{{\rm{i}}m\Delta t{\omega _j}}}} $ | (3) |
其中,
为方便描述,设满足奈奎斯特采样数据点数的条件为
Hankel矩阵是一种类斜对角矩阵,可由向量
| ${\bf{X}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{N - 1}}}&{{x_N}} \\ {{x_2}}&{{x_3}}& \cdots &{{x_N}}&{{x_{N + 1}}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{x_N}}&{{x_{N + 1}}}& \cdots &{{x_{2N - {\rm{2}}}}}&{{x_{2N - {\rm{1}}}}} \end{array}} \right]$ | (4) |
其中,
| ${\bf{X}} = {\bf{Rx}}$ | (5) |
这里,R是将FID信号x转换为Hankel矩阵X的算子.
FID的Hankel矩阵主要包含以下重要性质:(1)Hankel矩阵的秩R与谱峰个数J相等,即
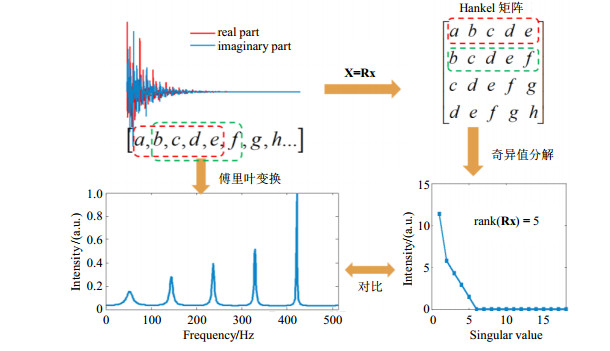
|
图 2 FID信号转Hankel矩阵及低秩特性.注:Hankel矩阵的非零奇异值个数(秩)等于谱峰个数,且与谱峰宽度无关,FID点数为511 Fig. 2 Transforming the FID signal into a Hankel matrix and its low rank property. Note: The number of non-zero singular values, i.e., rank, is equal to the number of spectral peaks and is independent on the width of peaks. The number of FID data points is 511 |
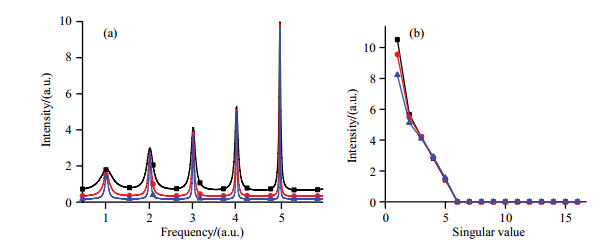
|
图 3 三种不同谱峰宽度的(a)谱峰和(b)谱的奇异值分布(非零奇异值的个数表示矩阵的秩)(根据文献[15]附录修改) Fig. 3 Independence of the rank on the peak line width. (a) Three simulated spectra with peaks of different widths; (b) Singular value curves of the three corresponding FIDs rearranged into the Hankel matrix (Reproduced from the appendix of Ref. [15]) |
LRHM解决的是FID在非均匀采样下的缺失数据恢复问题.其核心思想是将欠采样的FID信号转化成一个部分元素缺失的Hankel矩阵,具体流程如图 4所示.假定FID由数量有限的复指数函数组成,LRHM通过矩阵的低秩特性来重建FID,其数学模型为:
| $\mathop {\min }\limits_{\bf{x}} {\left\| {{\bf{Rx}}} \right\|_*} + \frac{\lambda }{2}\left\| {{\bf{y}} - {\bf{Ux}}} \right\|_2^2$ | (6) |
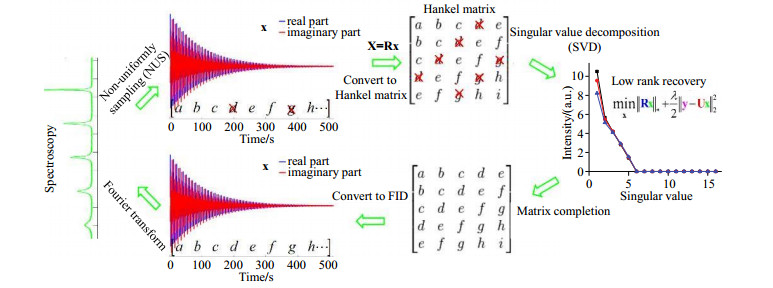
|
图 4 基于低秩Hankel矩阵重建NMR谱图的流程图(根据文献[15]修改) Fig. 4 The flowchart of NMR spectrum reconstruction with the low rank Hankel matrix method (Reproduced from Ref. [15]) |
其中,x为待重建的FID,y为欠采样的FID,U为欠采样算子,
由于时域FID的Hankel矩阵的秩不依赖于谱峰宽度[15],LRHM方法突破了现有的谱稀疏重建方法[11-14]对频谱内(频域)非零值数量的限制.仿真数据(图 5)和蛋白质NMR谱图(图 6)测试表明,LRHM方法可以克服最前沿的波谱稀疏重建方法—CS-NMR[13, 36]时的谱峰失真和丢失问题.
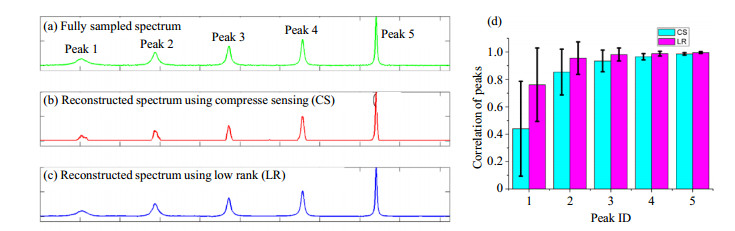
|
图 5 仿真指数函数在20%数据量的重建谱.(a)全采样谱图;(b)稀疏重建;(c)低秩重建;(d)各个谱峰的相关性(100次随机采样和重建实验)(摘自文献[15]).注:误差线是100个NUS实验中相关性的标准偏差 Fig. 5 Reconstructed spectra from 20% data of synthetic exponential functions. (a) The fully sampled spectrum; (b) and (c) are reconstructed spectra using compressed sensing (CS) and low rank (LR) method, respectively; (d) the correlation of each reconstructed peak and the original peak (Excerpted from Ref.[15]). Note: Error bars are the standard deviations of correlations in 100 NUS experiments |
|
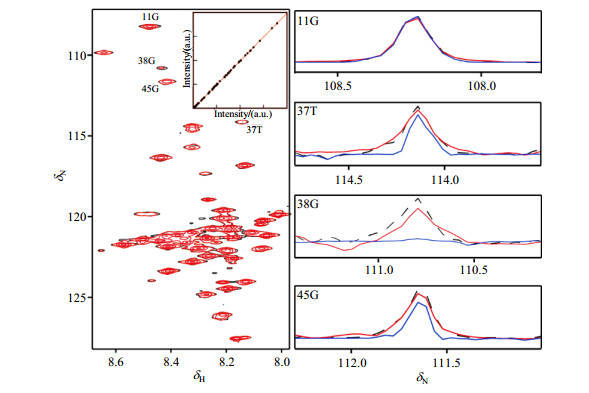
图 6 35%数据量的CD79b蛋白质的2D 1H-15N HSQC谱图.虚线、红色实线和蓝色实线分别表示全采样谱、低秩重建和稀疏重建的谱(根据文献[15]修改) Fig. 6 2D 1H-15N HSQC spectrum of 35% data of the cytosolic domain of CD79b. The dashed, red solid, and blue solid lines show 1D 15N-traces through the peaks in the fully sampled spectra, reconstructed spectrum using low rank method, and reconstructed one using compressed sensing method, respectively (Reproduced from Ref. [15]) |
在LRHM方法中,常用的快速数值算法有3种:交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[15]、无奇异值分解(Singular Value Decomposition-Free,SVD-Free)[5]和并行计算[5].
ADMM通过增广变量和交替迭代求解,是快速求解凸优化重建的典型数值算法.利用ADMM来求解LRHM问题[15],首先引入中间变量Z=Rx和拉格朗日乘子D,将(6)式中的优化问题转化为:
| $\mathop {\max }\limits_{\bf{D}} \mathop {\min }\limits_{{\bf{x}}, {\bf{Z}}} {\left\| {\bf{Z}} \right\|_*} + \frac{\lambda }{2}\left\| {{\bf{y}} - {\bf{Ux}}} \right\|_2^2 + \left\langle {{\bf{D}}, {\bf{Rx}} - {\bf{Z}}} \right\rangle + \frac{\beta }{2}\left\| {{\bf{Rx}} - {\bf{Z}}} \right\|_F^2$ | (7) |
其中,变量Z将核范数项和二范数项分离,β为大于0的参数(一般取1),
但是,核范数最小化在迭代算法中采用了耗时的SVD,SVD的计算复杂度与矩阵大小的幂呈正比[5], 导致在谱重建尤其是大规模Hankel矩阵的多维谱重建中明显增加重建时间.解决这一问题的一种有效方式就是避免耗时的SVD,即SVD-Free算法[5].目前,SVD-Free算法主要通过矩阵分解来回避SVD,又能很好地逼近核范数,计算公式如下:
| $\mathop {\min }\limits_{\bf{x}} \left\{ {\frac{1}{2}(\left\| {\bf{P}} \right\|_F^2 + \left\| {\bf{Q}} \right\|_F^2) + \frac{\lambda }{2}\left\| {{\bf{y - Ux}}} \right\|_2^2} \right\}{\rm{ s}}{\rm{.t}}{\rm{. }}{\bf{Rx}} = {\bf{P}}{{\bf{Q}}^H}$ | (8) |
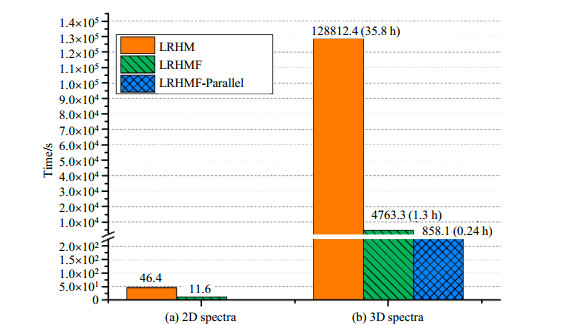
这一方法也被称为低秩Hankel矩阵分解方法(Low Rank Hankel Matrix Factorization,LRHMF).图 7所示的计算时间表明,与基于SVD的LRHM算法相比,LRHMF可以把2D谱和3D谱的重建时间分别降为1/4和1/27.即便如此,LRHMF重建3D谱的时间仍然达到1.3 h,还是比较长.
|
图 7 LRHM、LRHMF和LRHMF-Parallel谱重建时间比较(根据文献[5]修改).注:2D谱和3D谱的数据大小分别为256(t1间接维)×116(t2直接维)和128(t1间接维)×64(t2间接维)×512(t3直接维),3D谱的NUS在t1与t2形成的间接维平面进行非均匀采样.计算机GPU型号是具有24个计算核的Intel Xeon E5-2650v4 Fig. 7 Computation time of spectra reconstruction using LRHM, LRHMF methods with and without parallel computing (Reproduced from Ref. [5]). Note: The data size of the 2D and 3D NMR are 256 (t1 indirect dimension)×116 (t2 direct dimension), and 128 (t1 indirect dimension)×64 (t2 indirect dimension)×512 (t3 direct dimension), respectively. In 3D NMR, the NUS is performed on the t1-t2 plane. There are 24 computing cores in the Intel Xeon E5-2650v4 CPUs |
除上述外,现代计算机的多核心处理器允许采用并行任务以提高计算速度.以图 8所示的3D谱重建为例,低秩方法对每一个间接维平面的非均匀采样数据独立重建,因此可以把重建任务独立分配到多个处理核心.图 7所示并行计算把时间降低为LRHMF的

|
图 8 3D NMR谱的并行低秩重建(摘自文献[5]) Fig. 8 Parallel low rank reconstruction for 3D NMR spectrum(Excerpted from Ref. [5]) |
除了上述核范数最小化的基本方法及快速算法,研究者们还提出了降低谱重建误差和更高维谱重建的新方法.
LRHM在数学模型和NMR重建谱上存在一定局限.首先,作为秩的替代函数,核范数[37, 38]偏离了秩的严格数学定义(非零奇异值的个数)[图 9(a)],这意味着核范数最小化的LRHM方法[15]并没有直接约束NMR谱峰个数.其次,在重建中观察到当FID高度欠采样时,LRHM容易导致低强度谱峰丢失或减弱[图 9(b)].加权低秩Hankel矩阵(Weighted Low Rank Hankel Matrix,WLRHM)方法[6]通过对核范数加权以更好地逼近低秩约束.最理想的权重应该为奇异值倒数,但由于欠采样不存在真实信号而无法获得理想的权重,研究人员提出先通过LRHM预重建得到完整波谱再学习权重,以此达到更好地逼近Hankel矩阵的秩,从而降低重建谱误差[6].在蛋白质谱的测试表明,WLRHM在低采样率下能更好地保持低强度谱峰,防止谱峰丢失(图 10)和峰高降低(图 11).

|
图 9 核范数最小化的局限性.(a)秩与核范数的比较;(b)使用核范数最小化的LRHM重建谱.注:阿拉伯数字表示谱峰编号,从左到右谱峰宽度从宽到窄(根据文献[6]修改) Fig. 9 Limitations of nuclear norm minimization. (a) Comparisons between rank and nuclear norm; (b) Reconstructed NMR spectra using LRHM with nuclear norm minimization. Note: The Arabic numerals denote the identifier on spectral peaks of the ground truth spectrum. From left to right, the peak widths are from broad to narrow (Reproduced from Ref. [6]) |
|
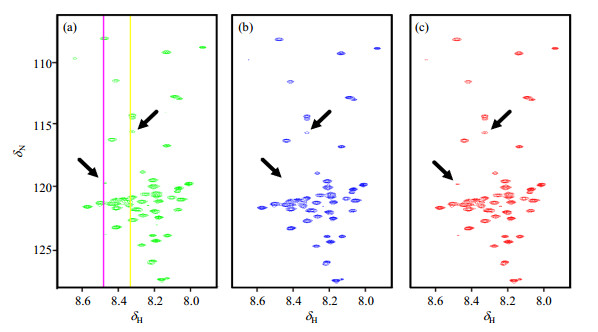
图 10 25%数据量重建2D HSQC谱.(a)全采样谱;(b)和(c)分别为LRHM和WLRHM重建的谱(根据文献[6]修改).注:全采样数据与图 6相同 Fig. 10 Reconstructed 2D HSQC spectrum from 25% data. (a) The fully sampled spectrum; (b) and (c) are reconstructed spectra using the LRHM and WLRHM, respectively (Reproduced from Ref. [6]). Note: The fully sampled data are the same as those in Fig. 6 |
|
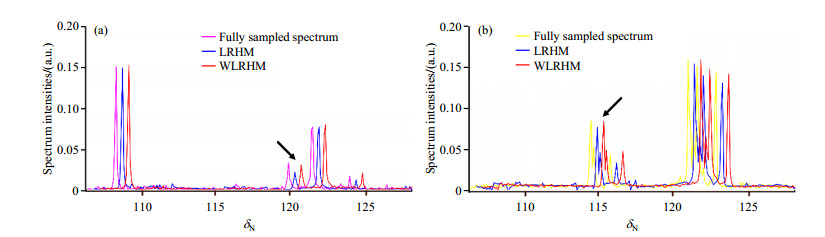
图 11 重建的2D HSQC谱的1D谱线.(a)和(b)分别取自图 10(a)中的紫色和黄色线.注意:为了获得更好的可视化效果,1D谱被稍微移动了距离(根据文献[6]修改) Fig. 11 1D traces of reconstructed 2D HSQC spectra. (a) and (b) are taken at the purple and yellow lines in Fig. 10(a), respectively. Note: 1D traces of reconstruction are shifted for better visualization (Reproduced from Ref. [6]) |
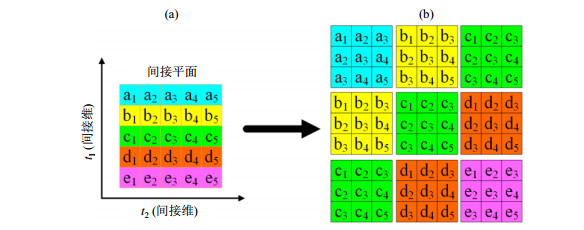
典型的LRHM方法只能重建1D信号的欠采样(图 4),并应用于2D谱中的间接维欠采样重建,无法重建3D甚至更多维NMR谱.以3D谱为例,非均匀采样实施在t1和t2组成的间接维平面(图 8)以达到加速NMR采样目的.为重建2D平面的非均匀采样信号,研究者又提出一种基于低秩分块Hankel矩阵(Low Rank Block Hankel Matrix,LRBHM)的NMR重建方法[5].该方法的核心在于构建分块Hankel矩阵(图 12),首先将每一行转化为Hankel矩阵,然后把这些Hankel矩阵视为单个元素并填充组合得到分块Hankel矩阵.由于分块Hankel矩阵的秩等于2D谱的谱峰数,如果2D FID中谱峰数量远远小于数据点的数量,则分块Hankel矩阵是低秩的,也可以用核范数最小化进行重建[5, 39].需要指出,由于构造的分块Hankel矩阵规模很大,SVD时间长,需要采用2.1.3节提到的SVD-Free算法和并行计算[5].
|
图 12 构造分块Hankel矩阵的示例图.(a)间接维平面的FID;(b)分块Hankel矩阵(摘自文献[5]) Fig. 12 An illustrative example of transforming (a) 2D NUS data into (b) block Hankel matrix. (Excerpted from Ref. [5]) |
对于更多维(大于3D)的非均匀采样,虽然可以构造更多维度的分块Hankel矩阵,但矩阵规模非常大、难以求解.为解决这一棘手问题,研究人员提出一种Hankel矩阵核范数正则化的CP低秩张量补全(Hankel Matrix Nuclear Norm Regularized Tensor Completion,HMRTC)方法[32],其信号假设包括两个方面[图 13(a)]:(1)多维谱可以表示成多维空间中单个谱峰相加,单个谱峰所属多维空间的CANDECOMP/PARAFAC(CP)张量的秩为1,R个谱峰张量的秩为R,由于谱峰个数远小于多维谱数据点数,因此多维谱的张量是低秩的;(2)单个多维谱峰可以由各维的单个指数函数外乘得到,如果将该1D指数函数转化为Hankel矩阵,该矩阵的秩为1,且小于数据点数,因此每个指数函数的Hankel矩阵是低秩的.因此,可以同时约束CP张量低秩和Hankel矩阵低秩进行多维NUS的数据重建.研究人员曾提出过MDD并应用在蛋白质多维NMR谱重建[20].但是,MDD方法只利用了CP张量低秩,没有利用Hankel矩阵低秩来正则化每个维度的信号.在3D HNCO谱仿真的3D NUS重建表明[图 13(b)~(d)],HMRTC比CP张量低秩得到的重建谱更加完整,前者只需要10%的数据量即可重建高质量波谱.但是,目前HMRTC只是方法原型,因缺乏4D NMR数据的3D NUS数据等无法验证实测数据结果.

|
图 13 3D NMR谱与低秩张量重建.(a)基于多维指数的张量;(b)全采样的3D HNCO谱的投影;(c)和(d)分别是用低秩CP张量和HMRTC从10%数据的重建结果(根据文献[32]修改) Fig. 13 3D NMR spectra and low-rank tensor reconstruction. (a) Tensor with multi-dimensional exponential functions; (b) The 1H-15N and 1H-13C skyline projection spectra in the 3D HNCO experiment; (c) and (d) are reconstructions from 10% NUS data obtained by low-rank CP tensor and HMRTC, respectively (Reproduced from Ref. [32]) |
分子自扩散运动会导致NMR信号强度衰减[40].Johnson等[41]提出了DOSY谱,这种谱与传统2D谱(频率-频率)不同,其第一维是频率(即化学位移),第二维是扩散系数.不同组分的扩散系数一般不同,DOSY利用这一特性来分析复杂混合物中的各组分[42].
给定扩散排序谱H和拉普拉斯变换矩阵L,扩散衰减信号S可以表示为S=LH.由于矩阵L的病态性,直接由S经逆拉斯变换矩阵求解H会导致数值上不稳定,对噪声非常敏感.此外,扩散梯度的离散个数比扩散系数的离散个数少得多,使得反演问题存在无穷多个解.因此,可以引入正则化项求解H:
| $\mathop {\min }\limits_{\bf{H}} \left\| {{\bf{S}} - {\bf{LH}}} \right\|_F^2 + \lambda \Omega \left( {\bf{H}} \right)$ | (9) |
其中,
扩散系数不同组分的谱峰强度衰减曲线相似,导致能够分辨的组分数目较少或者难以分辨扩散系数接近的几个组分,所以实际应用中采取分而治之的策略[48].Yuan等[10]认为不同组分对应不同的扩散系数,同一组分不同基团的扩散谱相同.当组分数目较小时,矩阵H是低秩的,可通过逆拉普拉斯变换(Simultaneous Inversion of Laplace Transform,SILT)并用低秩约束DOSY,有利于降低各组分在扩散维的线性相关性.其模型如下:
| $\mathop {\min }\limits_{\bf{H}} \left\| {{\bf{S}} - {\bf{LH}}} \right\|_F^2 + \lambda {\left\| {\bf{H}} \right\|_*}{\rm{, s}}{\rm{.t}}{\rm{. }}{{\bf{H}}_{ik}} \geqslant 0$ | (10) |
其中
文献[10]对混合物M6的测试表明(图 14):典型的单指数拟合扩散系数容易出现孤立的伪扩散谱,从而导致组分区分错误[图 14(a)],SILT利用低秩特性得到的所有峰都出现在代表单个组分的实际自扩散系数的网格线上,能有效区分六个组分,提高了多变量分析方法的极限.对于DOSY谱峰重叠区域,由于低秩正则化重建后是一种线性叠加,可通过局部非负矩阵分解的方法解开重叠.

|
图 14 混合物M6的DOSY谱.(a)逐个谱峰单指数拟合结果,(b)低秩SILT方法结果.注:每个分子得出的扩散系数由网格线定义;峰重叠的区域用红色虚线矩形标记;黑色箭头指示偏离真实位置的峰.色带表示谱峰强度,数值越高,谱峰强度越强(根据文献[10]修改) Fig. 14 DOSY plot for the mixture M6 by peak-wise mono-exponential fit (a) and SILT-DOSY (b). The derived diffusion coefficient for each molecule is defined by the grid line. The regions with overlapped peaks are labeled with red dash rectangles. The black arrows indicate the peaks off the true positions. The colorbar represents peak intensity. The higher the value, the stronger peak intensity (Reproduced from Ref. [10]) |
但是,低秩SLIT方法是由多个衰减谱反演至扩散维,并没有充分利用DOSY谱(H矩阵)的在扩散维的稀疏性,也没有讨论多维DOSY的非均匀采样等问题[43].
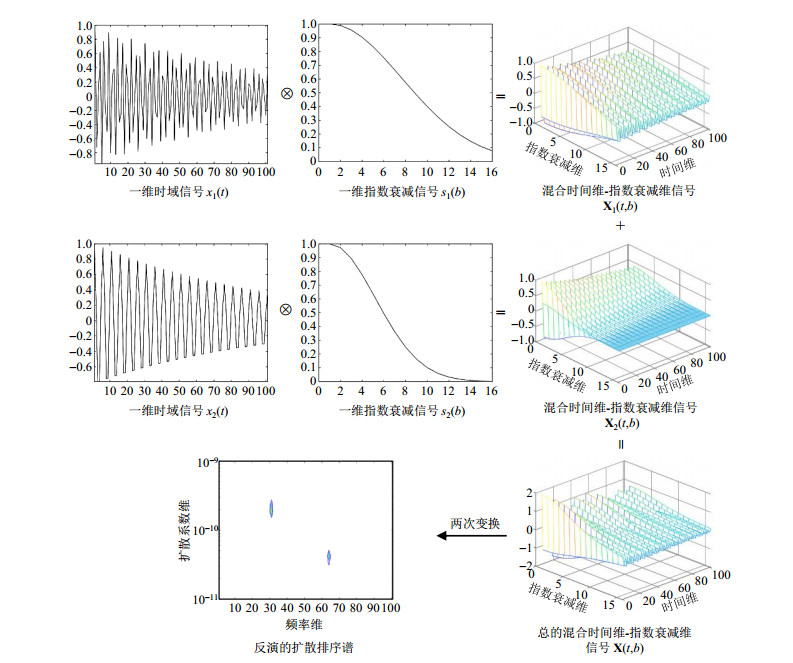
研究者提出一种结合稀疏和低秩特性的欠采样DOSY谱重建方法[45, 46].从采样信号角度分析,DOSY的时间域信号可以建模为混合时间维-指数衰减维信号
| ${\bf{X}}\left( {t, b} \right) = \sum\limits_{i = 1}^I {{x_i}(t) \otimes {s_i}(b)} $ | (11) |
其中,I表示1D时域信号的个数,
| ${s_i}\left( b \right) = \int_0^\infty {{h_i}\left( D \right)\exp \left( { - bD} \right){\rm{d}}D} $ | (12) |
其中,
|
图 15 混合时间维-指数衰减维信号的生成和反演(摘自文献[45]) Fig. 15 Generation and inversion of hybrid time and exponential decay signal in DOSY (Excerpted from Ref. [45]) |
研究人员提出结合低秩和稀疏特性的欠采样重建模型(Constraining Spectrum with Low Rank and Sparsity,CSLRS)[46]:
| $\mathop {\min }\limits_{\bf{h}} \frac{1}{2}\left\| {{\bf{UAh}} - {\bf{x}}} \right\|_2^2 + {\lambda _1}{\left\| {\bf{h}} \right\|_1} + {\lambda _2}{\left\| {{\bf{Ph}}} \right\|_*}$ | (13) |
其中,x表示欠采样混合信号的向量化形式,h表示扩散谱H的向量化形式,P表示向量转为矩阵的算子,A为傅里叶-拉普拉斯联合变换矩阵,
与只约束扩散谱稀疏性的多变量衰减迭代阈值方法(Iterative Thresholding Algorithm for Multiexponential Decay,ITAMeD)[43, 44]相比,CSLRS在混合物的DOSY谱(图 16)重建表明:CSLRS重建的峰型更好(如放大的正丙醇谱峰)、伪峰更少,而ITAMeD可能出现明显伪峰.

|
图 16 甲醇、乙醇和正丙醇溶于重水的DOSY谱重建结果.(a) CSLRS方法[45, 46];(b) ITAMeD方法[43, 44].注:采样10%数据且DOSY谱投影至直接维和扩散维(根据文献[45]修改) Fig. 16 DOSY spectra reconstruction of methanol, ethanol, and n-propanol in deuterium oxide. (a) CSLRS method[45, 46]; (b) ITAMeD method[43, 44]. Note: 10% data are sampled and the spectra are obtained by projecting to direct and diffusion dimensions (Reproduced from Ref. [45]) |
与只约束扩散谱低秩性的SILT方法[10]相比,研究人员提出全采样信号下[即(13)式中,欠采样矩阵U取单位阵]的联合低秩-稀疏逆拉普拉斯逆变换(Low-Rank and Sparse Inverse Laplace Transform,LRSpILT)[47]方法.混合样品数据的重建(图 17)表明:稀疏项的引入可以降低扩散谱的宽度,明显提高了扩散维方向的分辨率,便于从谱图上直接区分扩散系数比较接近的多个组分.

|
图 17 QGC样品的重建DOSY谱.(a)单指数拟合;(b)利用低秩特性的SILT方法;(c)利用低秩-稀疏特性的LRSpILT方法.注:红色矩形标记的是重叠谱峰,黑色箭头标记的是伪峰. QGC样品是奎宁、香叶醇和莰烯溶于氘代甲醇[摘自文献[47],(2020)美国化学学会版权所有] Fig. 17 Reconstructed spectra for experimental data QGC with (a) mono-exponential fitting, (b) SILT and (c) LRSpILT. Areas marked by the red rectangular are of overlapping peaks. Artifacts in Fig. (b) and (c) are marked with black arrows. The sample is named QGC, consisting of quinine, geraniol, and camphene dissolved in deuterated methanol. [Adapted with permission from Ref. [47]. copyright (2020) American Chemical Society] |
上述低秩重建利用的是扩散谱在化学位移(频率)-扩散二维平面整体的低秩特性,实验观察到重建波谱的基线会出现震荡现象[45].考虑频率维对应时间信号的指数函数特性,将FID低秩Hankel矩阵特性引入到DOSY谱重建中,研究人员提出基于LRHM的混合时间维-指数衰减维信号的重建原型(Constraining Spectrum with Low Rank Hankel Matrix and Sparsity,CSLRHMS)[45]:
| $\mathop {\min }\limits_{\bf{h}} \frac{1}{2}\left\| {{\bf{UAh}} - {\bf{x}}} \right\|_2^2 + {\lambda _1}{\left\| {\bf{h}} \right\|_1} + {\lambda _2}\sum\limits_{m = 1}^M {{{\left\| {{\bf{R}}{{\bf{Q}}_m}{\bf{Ah}}} \right\|}_*}} $ | (14) |
其中,算子
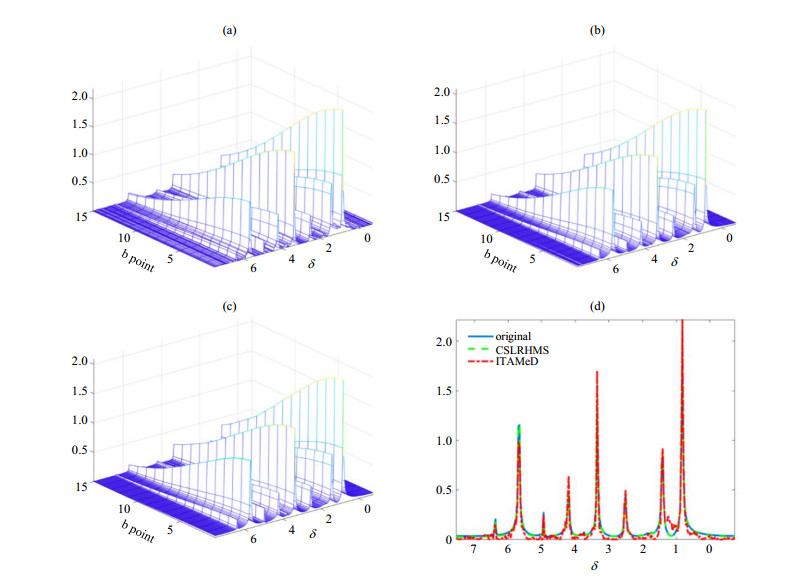
一个混合物的测试结果(图 18)表明,与典型稀疏重建方法ITAMeD[43, 44]相比,CSLRHMS的化学位移及基线重建结果更接近真实值,可以实现高保真谱重建.但是该方法还处于原型阶段,尚未分析DOSY扩散谱性能,也没有与扩散谱低秩的CSLRS方法相比.
|
图 18 实测正丙醇、二氢呋喃和二氯甲烷溶于氘代二甲基亚砜的信号恢复结果(10%采样率).(a) ITAMeD方法;(b) CSLRHMS方法;(c)全采样的混合频率维-指数衰减维信号;(d)第一个扩散梯度(m=1)下重建的1D谱(根据文献[45]修改) Fig. 18 DOSY spectra reconstruction of n-propanol, dihydrofuran and dichloromethane dissolved in deuterated dimethyl sulfoxide. (a) ITAMeD method; (b) CSLRHMS method; (c) Fully sampled hybrid frequency-exponential decay signal; (d) Reconstructed 1D spectra at the first diffusion gradient (Reproduced from Ref. [45]) |
低秩重建是一种新型的NMR波谱重建方法,它利用NMR波谱的低秩特性将指数信号转化为Hankel矩阵来重建频谱,并结合非均匀采样降低采集数据量从而缩短采样时间.该方法不仅适用于2D NMR波谱,还可结合张量等进一步拓展到更高维谱(维度≥3)重建.但是,当低强度NMR波谱受到噪声污染且噪声跟最低谱峰比较接近时,或加速采样倍数比较大导致波谱信号混叠严重时,噪声或伪峰的奇异值与真实谱峰很接近,容易导致低强度谱峰重建失真,如何开发高保真NMR波谱重建方法是一大挑战.此外,现有迭代重建方法需要几分钟到几十分钟,建立快速低秩Hankel矩阵重建数值算法,尤其是借鉴深度学习实现1 s内超快速算法[16]亟待探索.针对一些特殊的谱,诸如扩散谱或动态谱,如何更充分利用多维信息并验证在化学生物样品的实测优势尚需进一步佐证.总之,信号处理、机器学习和人工智能[23]的迅速发展,为快速采样、重建和分析多维高分辨率NMR波谱提供了令人激动的发展契机.
| [1] | BORGIA A, BORGIA M B, BUGGE K, et al. Extreme disorder in an ultrahigh-affinity protein complex[J]. Nature, 2018, 555(7694): 61-66. DOI: 10.1038/nature25762. |
| [2] | LIU G, LEVIEN M, KARSCHIN N, et al. One-thousand-fold enhancement of high field liquid nuclear magnetic resonance signals at room temperature[J]. Nat Chem, 2017, 9(7): 676-680. DOI: 10.1038/nchem.2723. |
| [3] | NGUYEN H M, PENG X, DO M N, et al. Denoising MR spectroscopic imaging data with low-rank approximations[J]. IEEE T Bio-Med Eng, 2013, 60(1): 78-89. DOI: 10.1109/TBME.2012.2223466. |
| [4] | HUANG Y, CAO S H, YANG Y, et al. Ultrahigh-resolution NMR spectroscopy for rapid chemical and biological applications in inhomogeneous magnetic fields[J]. Anal Chem, 2017, 89(13): 7115-7122. DOI: 10.1021/acs.analchem.7b01036. |
| [5] | GUO D, LU H, QU X B. A fast low rank Hankel matrix factorization reconstruction method for non-uniformly sampled magnetic resonance spectroscopy[J]. IEEE Access, 2017, 5: 16033-16039. DOI: 10.1109/ACCESS.2017.2731860. |
| [6] | GUO D, QU X B. Improved reconstruction of low intensity magnetic resonance spectroscopy with weighted low rank Hankel matrix completion[J]. IEEE Access, 2018, 6: 4933-4940. DOI: 10.1109/ACCESS.2018.2794478. |
| [7] | HILLER S, GARCES R G, MALIA T J, et al. Solution structure of the integral human membrane protein VDAC-1 in detergent micelles[J]. Science, 2008, 321(5893): 1206-1210. DOI: 10.1126/science.1161302. |
| [8] |
GAO D L, SUN P, WANG Q W, et al. Interactions between albumin and fatty acids studied by NMR spectroscopy[J].
Chinese J Magn Reson, 2018, 35(3): 338-344.
高东莉, 孙鹏, 王倩文, 等. 运用NMR研究白蛋白与脂肪酸的相互作用[J]. 波谱学杂志, 2018, 35(3): 338-344. |
| [9] | MOBLI M, HOCH J C. Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR[J]. Prog Nucl Magn Reson Spectrosc, 2014, 83: 21-41. DOI: 10.1016/j.pnmrs.2014.09.002. |
| [10] | YUAN B, DING Y, KAMAL G M, et al. Reconstructing diffusion ordered NMR spectroscopy by simultaneous inversion of Laplace transform[J]. J Magn Reson, 2017, 278: 1-7. DOI: 10.1016/j.jmr.2017.03.004. |
| [11] | QU X B, CAO X, GUO D, et al. Compressed sensing for sparse magnetic resonance spectroscopy[C]//18th Sci. Meeting Int Soc Magn Reson Med (ISMRM), Stockholm, Sweden. 2010, 10: 3371. |
| [12] | HOLLAND D J, BOSTOCK M J, GLADDEN L F, et al. Fast multidimensional NMR spectroscopy using compressed sensing[J]. Angew Chem Int Ed, 2011, 50(29): 6548-6551. DOI: 10.1002/anie.201100440. |
| [13] | KAZIMIERCZUK K, OREKHOV V Y. Accelerated NMR spectroscopy by using compressed sensing[J]. Angew Chem Int Ed, 2011, 123(24): 5670-5673. DOI: 10.1002/ange.201100370. |
| [14] | QU X B, GUO D, CAO X, et al. Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension[J]. Sensors, 2011, 11(9): 8888-8909. DOI: 10.3390/s110908888. |
| [15] | QU X B, MAYZEL M, CAI J F, et al. Accelerated NMR spectroscopy with low-rank reconstruction[J]. Angew Chem Int Ed, 2015, 54(3): 852-854. DOI: 10.1002/anie.201409291. |
| [16] | QU X B, HUANG Y H, LU H F, et al. Accelerated nuclear magnetic resonance spectroscopy with deep learning[J]. Angew Chem Int Ed, 2020, 132(26): 10383-10386. DOI: 10.1002/ange.201908162. |
| [17] | SIBISI S, SKILLING J, BRERETON R G, et al. Maximum entropy signal processing in practical NMR spectroscopy[J]. Nature, 1984, 311(5985): 446-447. DOI: 10.1038/311446a0. |
| [18] | BARNA C J, TAN S M, LADE E D. Use of CLEAN in conjunction with selective data sampling for 2D NMR experiments[J]. J Magn Reson, 1988, 78(2): 327-332. |
| [19] | COGGINS B E, ZHOU P. High resolution 4-D spectroscopy with sparse concentric shell sampling and FFT-CLEAN[J]. J Biomol NMR, 2008, 42(4): 225-239. DOI: 10.1007/s10858-008-9275-x. |
| [20] | JARAVINE V, IBRAGHIMOV I, OREKHOV V Y. Removal of a time barrier for high-resolution multidimensional NMR spectroscopy[J]. Nat Methods, 2006, 3(8): 605-607. DOI: 10.1038/nmeth900. |
| [21] | DRORI I. Fast minimization by iterative thresholding for multidimensional NMR spectroscopy[J]. Eurasip J Adv Sig Pr, 2007, 2007(1): 020248. DOI: 10.1155/2007/20248. |
| [22] | YING J F, DELAGLIO F, TORCHIA D A, et al. Sparse multidimensional iterative lineshape-enhanced (SMILE) reconstruction of both non-uniformly sampled and conventional NMR data[J]. J Biomol NMR, 2017, 68(2): 101-118. DOI: 10.1007/s10858-016-0072-7. |
| [23] | CHEN D C, WANG Z, GUO D, et al. Review and prospect:deep learning in nuclear magnetic resonance spectroscopy[J]. Chem-Eur J, 2020. |
| [24] |
ZHENG H, HAN M Y, HU B W, et al. Comparison of different sampling schemes in compressed sensing reconstruction for DQ-SQ experiments[J].
Chinese J Magn Reson, 2014, 31(4): 535-547.
郑慧, 韩明月, 胡炳文, 等. 不同采样模式的固体DQ-SQ实验的压缩感知重建比较[J]. 波谱学杂志, 2014, 31(4): 535-547. |
| [25] |
ZHANG Z Y, QU X B, LIN Y Q, et al. Sparse reconstruction algorithm of NMR spectrum based on minimizing approximate L0 norm[J].
Chinese J Magn Reson, 2013, 30(4): 528-540.
张正炎, 屈小波, 林雁勤, 等. 基于近似L0范数最小化的NMR波谱稀疏重建算法[J]. 波谱学杂志, 2013, 30(4): 528-540. DOI: 10.3969/j.issn.1000-4556.2013.04.006. |
| [26] |
NIE L S, JIANG B, ZHANG X, et al. A compressed sensing and resampling based noise suppression method for NMR[J].
Chinese J Magn Reson, 2016, 33(2): 244-256.
聂莉莎, 蒋滨, 张许, 等. 基于压缩感知/重采样的NMR噪声抑制新方法[J]. 波谱学杂志, 2016, 33(2): 244-256. |
| [27] | SHCHUKINA A, KASPRZAK P, DASS R, et al. Pitfalls in compressed sensing reconstruction and how to avoid them[J]. J Biomol NMR, 2016, 68(2): 79-98. |
| [28] | CANDÈS E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Proc Mag, 2008, 25(2): 21-30. DOI: 10.1109/MSP.2007.914731. |
| [29] | 张贤达. 矩阵分析及应用[M]. 北京: 清华大学出版社, 2015. |
| [30] | CANDÈS E J, RECHT B. Exact matrix completion via convex optimization[J]. Found Comput Math, 2009, 9(6): 717-772. DOI: 10.1007/s10208-009-9045-5. |
| [31] | CAI J F, CANDÈS E J, SHEN Z. A singular value thresholding algorithm for matrix completion[J]. SIAM J Optimiz, 2010, 20(4): 1956-1982. DOI: 10.1137/080738970. |
| [32] | YING J X, LU H, WEI Q. Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals[J]. IEEE T Signal Proce, 2017, 65(14): 3702-3717. DOI: 10.1109/TSP.2017.2695566. |
| [33] | KOEHL P. Linear prediction spectral analysis of NMR data[J]. Prog Nucl Magn Reson Spectrosc, 1999, 34(3, 4): 257-299. |
| [34] | MAN P P, BONHOMME C, BABONNEAU F. Denoising NMR time-domain signal by singular-value decomposition accelerated by graphics processing units[J]. Solid State Nucl Mag, 2014, 61: 28-34. |
| [35] | QIU T Y, LIAO W J, GUO D, et al. Gaussian noise removal with exponential functions and spectral norm of weighted Hankel matrices[J]. arXiv: 2001.11815, 2020. |
| [36] | MAYZEL M, KAZIMIERCZUK K, OREKHOV V Y. The causality principle in the reconstruction of sparse NMR spectra[J]. Chem Commun, 2014, 50(64): 8947-8950. DOI: 10.1039/C4CC03047H. |
| [37] | RECHT B, FAZEL M, PARRILO P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J]. SIAM Rev, 2010, 52(3): 471-501. DOI: 10.1137/070697835. |
| [38] | FAZEL M, PONG T K, SUN D F, et al. Hankel matrix rank minimization with applications to system identification and realization[J]. SIAM J Matrix Anal A, 2013, 34(3): 946-977. DOI: 10.1137/110853996. |
| [39] | LU H F, ZHANG X L, QIU T Y, et al. Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy[J]. IEEE T Bio-Med Eng, 2018, 65(4): 809-820. DOI: 10.1109/TBME.2017.2719709. |
| [40] | HAHN E L. Spin echoes[J]. Phys Rev, 1950, 80: 580-594. DOI: 10.1103/PhysRev.80.580. |
| [41] | MORRIS K F, JOHNSON C S. Diffusion-ordered two-dimensional nuclear magnetic resonance spectroscopy[J]. J Am Chem Soc, 1992, 114(8): 3139-3141. DOI: 10.1021/ja00034a071. |
| [42] |
HUANG J L, YU Y H. Effects of digital resolution on diffusional dimension in DOSY experiments[J].
Chinese J Magn Reson, 2018, 35(3): 287-293.
黄俊霖, 余亦华. 扩散序谱(DOSY)实验中扩散系数维数字分辨率的影响[J]. 波谱学杂志, 2018, 35(3): 287-293. |
| [43] | URBAŃCZYK M, KOŹMIŃSKI W, KAZIMIERCZUK K. Accelerating diffusion-ordered NMR spectroscopy by joint sparse sampling of diffusion and time dimensions[J]. Angew Chem Int Ed, 2014, 53(25): 6464-6467. DOI: 10.1002/anie.201402049. |
| [44] | URBAŃCZYK M, BERNIN D, KOŹMIŃSKI W, et al. Iterative thresholding algorithm for multiexponential decay applied to PGSE NMR data[J]. Anal Chem, 2013, 85(3): 1828-1833. DOI: 10.1021/ac3032004. |
| [45] | 张自飞.联合稀疏与低秩特性的磁共振扩散谱重建[D].厦门: 厦门大学, 2019. |
| [46] | 陈忠, 张自飞, 郭迪, 等.结合稀疏和低秩特性的欠采样磁共振扩散谱的重建方法: 中国, 10874832.4[P]. 2018-11-16. |
| [47] | LIN E P, YANG Y, HUANG Y Q, et al. High-resolution reconstruction for diffusion-ordered NMR spectroscopy[J]. Anal Chem, 2020, 92(1): 634-639. DOI: 10.1021/acs.analchem.9b03865. |
| [48] | COLBOURNE A A, MORRIS G A, NILSSON M. Local covariance order diffusion-ordered spectroscopy:a powerful tool for mixture analysis[J]. J Am Chem Soc, 2011, 133(20): 7640-7643. DOI: 10.1021/ja2004895. |
 2020, Vol. 37
2020, Vol. 37 
