2. 华东师范大学, 上海市磁共振重点实验室, 上海 200062;
3. 上海健康医学院, 上海市分子影像学重点实验室, 上海 201318;
4. 上海健康医学院, 医学影像学院, 上海 201318
2. Shanghai Key Laboratory of Magnetic Resonance, East China Normal University, Shanghai 200062, China;
3. Shanghai Key Laboratory of Molecular Imaging, Shanghai University of Medicine & Health Sciences, Shanghai 201318, China;
4. College of Medical Imaging, Shanghai University of Medicine & Health Sciences, Shanghai 201318, China
核磁共振(NMR)波谱是解析物质结构的重要技术.二维NMR[1]谱图可以将化学位移、耦合关系等参数在二维平面展开,降低谱线的重叠度,提高谱图分辨率,是大分子化合物结构解析[2]的常用方法.异核单量子相干(HSQC)脉冲序列[3]是大量二维NMR实验的基本组成部分,一些复杂的多脉冲序列也是由此基本序列演化而来.HSQC实验利用HSQC脉冲序列对自旋IS体系(一般是H-C或H-N)进行激发,得到两个独立的时域信号,经傅里叶变换即可得到二维NMR谱图[4].在特定脉冲的作用下,IS体系的双核之间发生了极化转移现象,具体表现为I核能级上的磁化量子布居数倒转[5],引起S核的极化发生变化,从而将灵敏度较高的I核的磁化矢量极化转移到低灵敏度的S核,进而提高了S核的NMR信号强度.HSQC实验的极化转移效率决定了谱图的质量,但是极化转移效率受实验参数设置和实验条件影响较大.即便是在最原始版本的HSQC实验中,也包含了10个脉冲(不考虑最后采样阶段的去耦脉冲),而任何一个脉冲的强度设置不当或者脉冲间隔时间改变,都会影响到最后的频谱信号,因此HSQC实验效果存在较大的不稳定性.利用计算机模拟HSQC实验,通过改变实验参数,可以获得相应的HSQC模拟谱图,对比模拟与实验的结果,对于指导获得高质量HSQC实验谱图具有重要意义.
计算机模拟是辅助NMR实验的重要工具[6, 7].通过理论计算对每次实验参数调整后的NMR谱图进行模拟和实验结果预测,可以有效减少实验开销;同时计算机模拟可以不受NMR实验条件的限制,获得理想的实验结果,有利于NMR实验的教学和脉冲序列的开发设计.自“NMR实验的计算机模拟”概念提出至今,研究人员开发了许多计算机程序来模拟NMR实验:GAMMA[8]作为NMR完整模拟程序包的经典开山之作,是面向对象的NMR仿真工具库,基于自旋体系的量子力学计算原理,能够模拟各种实验条件下的NMR现象,但它需要额外编写接口程序来执行模拟;SIMPSON[9]是一种通用的固体NMR实验模拟程序,计算过程遵循核自旋动力学与量子力学原理,并拥有可设置NMR实验相关条件的程序用户界面,通过将实验参数输入命令脚本来驱动模拟,但该程序对射频脉冲的适用性有限,且后续的数据处理需依赖外部软件完成,计算效率较低;SPINEVOLUTION[10]是液体和固体NMR实验模拟的优化程序,它在SIMPSON的基础上不仅提高了大型自旋系统的计算效率,而且优化了程序执行接口,非常适合作为构建复杂脉冲序列的有效模拟的框架.上述三种程序是用于NMR模拟的经典程序,基于自旋动力学与量子力学原理,采用哈密顿量描述NMR实验中的所有相互作用,利用乘积算符建立自旋密度矩阵演化方程并进行编程计算,实现NMR实验的模拟,后续NMR模拟程序[11, 12]都是以这类算法的原理为基础优化与发展而来.
本文遵循NMR计算机模拟的基本流程,通过量子化学计算,推导自旋1/2的双核体系的角动量算符,计算了自旋体系在HSQC脉冲作用下的密度矩阵演化方程,最后采用二维NMR实验数据的采集与处理方法,专门针对液体NMR中的HSQC实验构建了Matlab模拟程序,模拟过程中无需额外编写调用脚本,只需根据实际实验参数的设置调整模拟参数、输入被测样品的化学位移与耦合作用参数、执行模拟程序便能得到HSQC模拟谱图,而且整个计算过程可以精确追踪实验每个脉冲节点的作用效果.
1 HSQC模拟设计根据图 1所示的NMR计算机模拟的经典流程[13],本文实现模拟主要分为三个步骤:第一步计算自旋体系的自旋基算符,根据化学位移和J耦合常数构建哈密顿函数;第二步将脉冲序列转换成旋转算符瞬时作用于自旋基算符,从而建立密度矩阵随时间演化的方程;第三步根据二维NMR信号的采集方法对密度矩阵中的自旋信号进行检测和采样,并对时域信号进行二维傅里叶变换生成NMR频谱图.

|
图 1 计算机模拟NMR实验的经典流程图 Fig. 1 The classical flow diagram of NMR simulation |
在量子力学的描述中,自旋核在空间坐标系各方向的自旋角动量分量可用自旋算符表示,自旋1/2的单核自旋算符定义[14]如下:
| $ {\mathit{\boldsymbol{I}}_z} = \frac{1}{2}\left. {\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{ - 1} \end{array}} \right.} \right], {\mathit{\boldsymbol{I}}_x} = \frac{1}{2}\left. {\left[ {\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right.} \right], {\mathit{\boldsymbol{I}}_y} = \frac{1}{2}\left. {\left[ {\begin{array}{*{20}{c}} 0&{ - {\rm{i}}}\\ {\rm{i}}&0 \end{array}} \right.} \right], $ | (1) |
其中,Iz、Ix、Iy分别表示自旋核在z、x、y轴方向的角动量算符.
根据相关文献,多核体系的自旋算符不仅可根据其物理定义求得[15],也可通过计算单核自旋算符的直积[16]得到,本文使用该方法计算自旋1/2双核体系的自旋算符,结果由表 1所示.其中,Sz、Sx、Sy分别表示S核在z、x、y轴方向的角动量算符,E是单位矩阵,下标(2×2)表示矩阵大小.
| 表 1 自旋1/2双核体系的自旋算符 Table 1 Product operators of two coupled spins with spin of 1/2 |
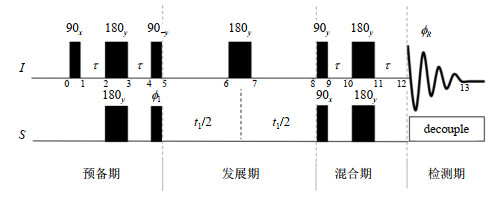
二维NMR实验包括四个脉冲作用阶段:预备期、发展期、混合期、检测期[17].预备期内自旋系统为相干的非平衡态,主要包括极化转移、低灵敏度核的极化增强;发展期又称演化期,自旋系统在哈密顿的作用下自由演化,也可添加脉冲去耦;混合期可将实验中单量子相干转化成可供观测的磁化矢量,增加图谱信息;检测期测量的是I核在t2期间磁化矢量的演化,是二维谱中直接维的特征信号,而间接维的信号是在发展期t1时间内产生的.
作用在IS体系上的HSQC基本脉冲序列[18]如图 2所示.其中脉冲注释的格式为θφ,θ表示射频脉冲翻转角,是脉冲持续时间的描述,φ表示脉冲作用的方向,主要为x,y;ϕ描述脉冲的相位,其中ϕ1是相位变量,ϕR表示信号接收相位;τ表示脉冲的间隔时间,即时延参数;数字0~13用于标记各脉冲作用的节点.在HSQC实验中,脉冲序列分为图示两个通道,I核通道与S核通道的脉冲有着不同的频率,只激发该通道的自旋核,最后在I核通道采集信号.
在自旋1/2的IS体系中,两自旋核化学位移的对应频率分别记作ωI、ωS,耦合常数记作JIS,单位为Hz.整个过程中IS体系受到相互作用的哈密顿量[14]为:
| $ \mathit{\boldsymbol{H}} = {\omega _I}{\mathit{\boldsymbol{I}}_z} + {\omega _S}{\mathit{\boldsymbol{S}}_z} + 2{\rm{ \mathsf{ π} }}{J_{IS}}{\mathit{\boldsymbol{I}}_z}{\mathit{\boldsymbol{S}}_z} $ | (2) |
HSQC脉冲预备期是一组低灵敏核的极化转移增强(INEPT)脉冲[19],它的作用是把高灵敏度I核的自旋极化传递给低灵敏度的S核,用于提高S核的信号强度.在稳定外磁场B0的作用下,IS体系初始状态的密度矩阵为:
| $ {\mathit{\boldsymbol{\rho }}_0} = {\mathit{\boldsymbol{I}}_z} + {\mathit{\boldsymbol{S}}_z} $ | (3) |
在I核通道施加x方向的90°瞬时脉冲,I核z方向上的自旋分量在脉冲作用下的演化方程为:
| $ {{\mathit{\boldsymbol{\rho }}}_1} = \exp [ - {\rm{i}}{{({\rm{\pi }}} \mathord{\left/ {\vphantom {{({\rm{\pi }}} 2}} \right. } 2}){{\mathit{\boldsymbol{I}}}_x}]{{\mathit{\boldsymbol{\rho }}}_0}\exp [{\rm{i}}{{({\rm{\pi }}} \mathord{\left/ {\vphantom {{({\rm{\pi }}} 2}} \right. } 2}){{\mathit{\boldsymbol{I}}}_x}] = - {{\mathit{\boldsymbol{I}}}_y} + {{\mathit{\boldsymbol{S}}}_z} $ | (4) |
该方程的结果表示I核自旋矢量翻转到-y轴,得到横向磁化.在2τ期间,对I核与S核通道施加y方向上的180°反转脉冲,在系统哈密顿量作用下的密度矩阵演化为:
| $ \begin{array}{l} {\mathit{\boldsymbol{\rho }}_4} = \exp ( - {\rm{i}}\mathit{\boldsymbol{H}}\tau )\exp [ - {\rm{i}}\pi ({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_y})]\exp ( - {\rm{i}}\mathit{\boldsymbol{H}}\tau ){\mathit{\boldsymbol{\rho }}_1}\exp ({\rm{i}}\mathit{\boldsymbol{{\rm H}}}\tau )\exp [{\rm{i}}\pi ({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_y})]\exp ( - {\rm{i}}\mathit{\boldsymbol{H}}\tau )\\ \;\;\;\;\; = - {\mathit{\boldsymbol{I}}_y}\cos (2\pi {J_{IS}}\tau ) + 2{\mathit{\boldsymbol{I}}_x}{\mathit{\boldsymbol{S}}_z}\sin (2\pi {J_{IS}}\tau ) - {\mathit{\boldsymbol{S}}_z} \end{array} $ | (5) |
由于系统哈密顿的作用,I核的密度矩阵包含化学位移项和耦合项.为了消除耦合项,令脉冲间隔τ=1/(4JIS),化简(5)式可得:
| $ {\mathit{\boldsymbol{\rho }}_4} = 2{\mathit{\boldsymbol{I}}_x}{\mathit{\boldsymbol{S}}_z} - {\mathit{\boldsymbol{S}}_z} $ | (6) |
此时I核受到了S核的耦合调制,同时实现化学位移在x轴的重聚,最后得到相对于x轴的反向磁化IxSz.然后在I核通道施加-y方向的90°瞬时脉冲,取ϕ1=90°x,在S核通道施加90°瞬时脉冲,密度矩阵演化为:
| $ {\mathit{\boldsymbol{\rho }}_{{\kern 1pt} 5}} = \exp \left\{ { - {\rm{i[}}({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. } 2}){\mathit{\boldsymbol{I}}_y} + ({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}){\mathit{\boldsymbol{I}}_x}]} \right\}{\mathit{\boldsymbol{\rho }}_{{\kern 1pt} 4}}\exp \left\{ {{\rm{i[}}({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. } 2}){\mathit{\boldsymbol{I}}_y} + (\pi /2){\mathit{\boldsymbol{I}}_x}]} \right\} = - 2{\mathit{\boldsymbol{I}}_z}{\mathit{\boldsymbol{S}}_y} + {\mathit{\boldsymbol{S}}_y} $ | (7) |
此时I核的磁化矢量回到z轴,产生的IxSz项实现了I核与S核之间的极化转移.
发展期的作用是标记S核化学位移的演化.经过t1/2时刻在I核通道y方向施加180°脉冲,密度矩阵的演化方程为:
| $ \begin{array}{l} {\mathit{\boldsymbol{\rho }}_8} = \exp ( - {\rm{i}}\mathit{\boldsymbol{H}}{{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} 2}} \right. } 2})\exp ( - {\rm{i}}\pi {\mathit{\boldsymbol{I}}_y})\exp ( - {\rm{i}}\mathit{\boldsymbol{H}}{{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} 2}} \right. } 2}){\mathit{\boldsymbol{\rho }}_5}\exp ({\rm{i}}\mathit{\boldsymbol{H}}{{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} 2}} \right. } 2})\exp ({\rm{i}}\pi {\mathit{\boldsymbol{I}}_y})\exp ({\rm{i}}\mathit{\boldsymbol{H}}{{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} 2}} \right. } 2})\\ \;\;\;\; = 2{\mathit{\boldsymbol{I}}_z}{\mathit{\boldsymbol{S}}_y}\cos ({\omega _s}{t_1}) - 2{\mathit{\boldsymbol{I}}_z}{\mathit{\boldsymbol{S}}_x}\sin ({\omega _s}{t_1}) \end{array} $ | (8) |
此时体系中的耦合作用被重聚,只剩下S核化学位移的演化.
混合期是一组反转INEPT脉冲.对I核通道施加y方向的90°脉冲,S核通道施加x方向的90°脉冲,密度矩阵演化如下:
| $ {\mathit{\boldsymbol{\rho }}_9} = \exp [ - {\rm{i}}(\pi /2)({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_x})]{\mathit{\boldsymbol{\rho }}_8}\exp [{\rm{i}}(\pi /2)({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_x})] = 2{\mathit{\boldsymbol{I}}_x}{\mathit{\boldsymbol{S}}_z}\cos ({\omega _s}{t_1}) - 2{\mathit{\boldsymbol{I}}_x}{\mathit{\boldsymbol{S}}_x}\sin ({\omega _s}{t_1}) $ | (9) |
此时I核上的90°脉冲使极化从S核转移回I核,I核磁化矢量翻转至x轴.在2τ中间对体系双通道施加y方向的180°脉冲,密度矩阵演化为:
| $ \begin{array}{l} {\mathit{\boldsymbol{\rho }}_{12}} = \exp ( - {\rm{i}}\mathit{\boldsymbol{H}}\tau )\exp [ - {\rm{i}}\pi ({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_y})]\exp ( - {\rm{i}}\mathit{\boldsymbol{H}}\tau ){\mathit{\boldsymbol{\rho }}_9}\exp ({\rm{i}}\mathit{\boldsymbol{H}}\tau )\exp [{\rm{i}}\pi ({\mathit{\boldsymbol{I}}_y} + {\mathit{\boldsymbol{S}}_y})]\exp ({\rm{i}}\mathit{\boldsymbol{H}}\tau )\\ \;\;\;\;\; = {\mathit{\boldsymbol{I}}_y}\cos ({\omega _s}{t_1}) - 2{\mathit{\boldsymbol{I}}_x}{\mathit{\boldsymbol{S}}_x}\sin ({\omega _s}{t_1}) \end{array} $ | (10) |
此时的脉冲实现了I核磁化分量的重聚,并产生自旋回波信号,使得采样能从回波信号最大值开始.对I核通道进行信号采样,采集到I核的磁化矢量信息中包含了S核的化学位移信息和耦合信息.
综上,IS体系在HSQC脉冲作用下,I核密度矩阵演化过程为:
| $ \begin{align} & {\mathit{\boldsymbol{I}}_{z}}\xrightarrow{{{90}^{\circ }}{\mathit{\boldsymbol{I}}_{x}}}-{\mathit{\boldsymbol{I}}_{y}}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{y}})}2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{z}}\xrightarrow{{{90}^{\circ }}(-{\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{x}})}-2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{y}} \\ & \xrightarrow[\mathit{\boldsymbol{H}}{{t}_{1}}]{{{180}^{\circ }}{\mathit{\boldsymbol{I}}_{y}}}2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{y}}\cos ({{\omega }_{s}}{{t}_{1}})-2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}}) \\ & \xrightarrow{{{90}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{x}})}2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{z}}\cos ({{\omega }_{s}}{{t}_{1}})-2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}}) \\ & \xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{y}})}{\mathit{\boldsymbol{I}}_{y}}\cos ({{\omega }_{s}}{{t}_{1}})-2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}}) \end{align} $ | (11) |
为了满足信号正交检测[20]的要求,当脉冲序列中ϕ1=-90°y时可获得Iy对应的正弦信号,密度矩阵演化方程如下:
| $ \begin{align} & {\mathit{\boldsymbol{I}}_{z}}\xrightarrow{{{90}^{\circ }}{\mathit{\boldsymbol{I}}_{x}}}-{\mathit{\boldsymbol{I}}_{y}}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{y}})}2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{z}}\xrightarrow{-{{90}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{y}})}-2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{x}} \\ & \xrightarrow[\mathit{\boldsymbol{H}}{{t}_{1}}]{{{180}^{\circ }}{\mathit{\boldsymbol{I}}_{y}}}2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{x}}\cos ({{\omega }_{s}}{{t}_{1}})+2{\mathit{\boldsymbol{I}}_{z}}{\mathit{\boldsymbol{S}}_{y}}\sin ({{\omega }_{s}}{{t}_{1}}) \\ & \xrightarrow{{{90}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{x}})}2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{x}}\cos ({{\omega }_{s}}{{t}_{1}})+2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{z}}\sin ({{\omega }_{s}}{{t}_{1}}) \\ & \xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({\mathit{\boldsymbol{I}}_{y}}+{\mathit{\boldsymbol{S}}_{y}})}{\mathit{\boldsymbol{I}}_{y}}\sin ({{\omega }_{s}}{{t}_{1}})+2{\mathit{\boldsymbol{I}}_{x}}{\mathit{\boldsymbol{S}}_{x}}\cos ({{\omega }_{s}}{{t}_{1}}) \end{align} $ | (12) |
HSQC脉冲序列INEPT模块中的时延参数τ决定了实验的极化转移效率,在实际应用中该参数通常需额外设置为某一定值,此时HSQC实验密度矩阵演化过程表示如下:
| $ \begin{align} & {{\mathit{\boldsymbol{I}}}_{z}}\xrightarrow{{{90}^{\circ }}{{\mathit{\boldsymbol{I}}}_{x}}}-{{\mathit{\boldsymbol{I}}}_{y}}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}-{{\mathit{\boldsymbol{I}}}_{y}}\cos (2\pi {{J}_{IS}}\tau )+2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{z}}\sin (2\pi {{J}_{IS}}\tau )-{{\mathit{\boldsymbol{S}}}_{z}} \\ & \xrightarrow{{{90}^{\circ }}(-{{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{x}})}-{{\mathit{\boldsymbol{I}}}_{y}}\cos (2\pi {{J}_{IS}}\tau )-2{{\mathit{\boldsymbol{I}}}_{z}}{{\mathit{\boldsymbol{S}}}_{y}}\sin (2\pi {{J}_{IS}}\tau ) \\ & \xrightarrow[\mathit{\boldsymbol{H}}{{t}_{1}}]{{{180}^{\circ }}{{\mathit{\boldsymbol{I}}}_{y}}}-{{\mathit{\boldsymbol{I}}}_{y}}\cos (2\pi {{J}_{IS}}\tau )+[2{{\mathit{\boldsymbol{I}}}_{z}}{{\mathit{\boldsymbol{S}}}_{y}}\cos ({{\omega }_{s}}{{t}_{1}})-2{{\mathit{\boldsymbol{I}}}_{z}}{{\mathit{\boldsymbol{S}}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}})]\sin (2\pi {{J}_{IS}}\tau ) \\ & \xrightarrow{{{90}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{x}})}-{{\mathit{\boldsymbol{I}}}_{y}}\cos (2\pi {{J}_{IS}}\tau )+[2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{z}}\cos ({{\omega }_{s}}{{t}_{1}})-2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}})]\sin (2\pi {{J}_{IS}}\tau ) \\ & \xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}[-{{\mathit{\boldsymbol{I}}}_{y}}\cos (2\pi {{J}_{IS}}\tau )+2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{z}}\sin (2\pi {{J}_{IS}}\tau )]\cos (2\pi {{J}_{IS}}\tau ) \\ & +[2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{z}}\cos (2\pi {{J}_{IS}}\tau )+{{\mathit{\boldsymbol{I}}}_{y}}\sin (2\pi {{J}_{IS}}\tau )]\cos ({{\omega }_{s}}{{t}_{1}})\sin (2\pi {{J}_{IS}}\tau )-2{{\mathit{\boldsymbol{I}}}_{x}}{{\mathit{\boldsymbol{S}}}_{x}}\sin ({{\omega }_{s}}{{t}_{1}})\sin (2\pi {{J}_{IS}}\tau ) \\ \end{align} $ | (13) |
保留异核相干项与可观测项,上述密度矩阵演化结果可简化为:
| $ {{\mathit{\boldsymbol{\rho }}}_{{\rm{12}}}}' = {I_y}\cos ({\omega _s}{t_1}){\sin ^2}(2\pi {J_{IS}}\tau ) $ | (14) |
对比时延参数τ在理论设置下的演化结果,表明当τ设置为某一定值时,HSQC实验的极化转移效率与自旋体系的耦合作用有关,信号强度与sin2(2πJISτ) 呈正比.
1.3 HSQC模拟信号的采集与处理根据HSQC基本脉冲的磁化矢量演化过程,可得检测期的密度矩阵为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\rho}} _{{\rm{cos}}}}({t_1}) = {{\mathit{\boldsymbol{I}}}_y}\cos ({\omega _s}{t_1}) - 2{{\mathit{\boldsymbol{I}}}_x}{{\mathit{\boldsymbol{S}}}_x}\sin ({\omega _s}{t_1})\\ {\mathit{\boldsymbol{\rho}} _{{\rm{sin}}}}({t_1}) = {{\mathit{\boldsymbol{I}}}_y}\sin ({\omega _s}{t_1}) + 2{{\mathit{\boldsymbol{I}}}_x}{{\mathit{\boldsymbol{S}}}_x}\cos ({\omega _s}{t_1}) \end{array} \right. $ | (15) |
式中IxSx是不可观测的双量子相干项[21],对自由感应衰减(FID)信号无贡献,可简化不计.
在I核通道采样期间,IS体系仍在自由进动,但是S核的共振和异核间耦合作用被解耦脉冲平均化为0,因此系统在t2采样期间哈密顿量可简化为:
| $ {\mathit{\boldsymbol{H}}_r} = {\omega _I}{\mathit{\boldsymbol{I}}_z} $ | (16) |
采样时的信号可表示为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\rho }}}_{{\rm{cos}}}}({t_1},{t_2}) = \exp ( - {\rm{i}}{{\mathit{\boldsymbol{H}}}_r}{t_2}){{\mathit{\boldsymbol{\rho }}}_{{\rm{cos}}}}({t_1})\exp ({\rm{i}}{{\mathit{\boldsymbol{H}}}_r}{t_2})\\ {{\mathit{\boldsymbol{\rho }}}_{{\rm{sin}}}}({t_1},{t_2}) = \exp ( - {\rm{i}}{{\mathit{\boldsymbol{H}}}_r}{t_2}){{\mathit{\boldsymbol{\rho }}}_{{\rm{sin}}}}({t_1})\exp ({\rm{i}}{{\mathit{\boldsymbol{H}}}_r}{t_2}) \end{array} \right. $ | (17) |
使用I核的观测算符[15]记录FID信号如下:
| $ \left\{ \begin{array}{l} FI{D_{\cos }}({t_1},{t_2}) = Tr\left\{ {{\mathit{\boldsymbol{I}}^{{ + }}}\left[ {{\mathit{\boldsymbol{\rho}} _{\cos }}({t_1},{t_2})} \right]} \right\}\exp ( - {{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} {{T_1}}}} \right. } {{T_1}}})\exp ( - {{{t_2}} \mathord{\left/ {\vphantom {{{t_2}} {{T_2}}}} \right. } {{T_2}}})\\ FI{D_{\sin }}({t_1},{t_2}) = Tr\left\{ {{\mathit{\boldsymbol{I}}^{{ + }}}\left[ {{\mathit{\boldsymbol{\rho}} _{\sin }}({t_1},{t_2})} \right]} \right\}\exp ( - {{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} {{T_1}}}} \right. } {{T_1}}})\exp ( - {{{t_2}} \mathord{\left/ {\vphantom {{{t_2}} {{T_2}}}} \right. } {{T_2}}}) \end{array} \right. $ | (18) |
式中Tr表示取矩阵的迹运算、I+表示I核的观测算符,用于获取自旋核的信号;exp(-t1/T1)、exp(-t2/T2)分别表示在采样期间各自旋核横向磁化矢量的衰减指数.随着t1阶段性递增而采集一次t2期间的信号,最后组成一个二维信号矩阵,信号采样方案如图 3所示.
采样得到的时域信号需要经过傅里叶变换形成频谱图,得到纯吸收型二维NMR频谱的方法有States[15]、TPPI[22]等,本文采用的是States方法.该方法首先将每次正交采样得到的正弦和余弦时域信号对t2进行一次傅里叶变换,分别得到FIDcos(t1, ω2)的实部作为信号的实部,FIDsin(t1, ω2)的实部作为信号的虚部,组成信号:
| $ {{S}_{\text{States}}}({{t}_{1}}, {{\omega }_{2}})=\operatorname{Re}\left[ FI{{D}_{\cos }}({{t}_{1}}, {{\omega }_{2}}) \right]\text{+i Re}\left[ FI{{D}_{\sin }}({{t}_{1}}, {{\omega }_{2}}) \right] $ | (19) |
最后将信号进行t1维的傅里叶变换,并取实部作为频域信号.
1.4 HSQC模拟程序的实现基于上述流程与方法,本文进一步在Matlab平台编写计算程序,执行HSQC实验的模拟,实现方案如下:
(1)设置可输入变量.
实验参数:数据矩阵(m,n),其中m表示间接维的数据点数,n表示直接维的数据点数;演化期时长t1;采样时间t2;时域信号衰减系数T1、T2,单位为ms;针对时延参数τ提供默认选项τ=1/(4JIS)、自由输入选项τ,单位为ms.
样品参数:化学位移对应频率ω,单位为kHz;耦合常数J,单位为Hz.
(2)设置自旋体系参数:自旋算符,观测算符,哈密顿函数H,初始密度矩阵ρ0.
(3)计算在HSQC脉冲作用下,自旋体系的密度矩阵从初态到终态的演化过程:
| $ \left\{ \begin{align} & {{\mathit{\boldsymbol{\rho}}_{0}}}\xrightarrow{{{90}^{\circ }}{{\mathit{\boldsymbol{I}}}_{x}}}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}\xrightarrow{{{90}^{\circ }}(-{{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{x}})}\xrightarrow[\mathit{\boldsymbol{H}}{{t}_{1}}]{{{180}^{\circ }}{{\mathit{\boldsymbol{I}}}_{y}}}\xrightarrow{{{90}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{x}})}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}{{\mathit{\boldsymbol{\rho}} }_{cos}}({{t}_{1}}) \\ & {{\mathit{\boldsymbol{\rho}}_{0}}}\xrightarrow{{{90}^{\circ }}{{\mathit{\boldsymbol{I}}}_{x}}}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}\xrightarrow{-{{90}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}\xrightarrow[\mathit{\boldsymbol{H}}{{t}_{1}}]{{{180}^{\circ }}{{\mathit{\boldsymbol{I}}}_{y}}}\xrightarrow{{{90}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{x}})}\xrightarrow[\mathit{\boldsymbol{H}}\cdot 2\tau ]{{{180}^{\circ }}({{\mathit{\boldsymbol{I}}}_{y}}+{{\mathit{\boldsymbol{S}}}_{y}})}{{\mathit{\boldsymbol{\rho}} }_{sin}}({{t}_{1}}) \\ \end{align} \right. $ |
(4)采样期间密度矩阵的演化:
| $ \left\{ \begin{align} & {{\mathit{\boldsymbol{\rho}} }_{cos}}({{t}_{1}})\xrightarrow{{{\mathit{\boldsymbol{H}}}_{r}}{{t}_{2}}}{{\mathit{\boldsymbol{\rho }}}_{cos}}({{t}_{1}},{{t}_{2}}) \\ & {{\mathit{\boldsymbol{\rho }}}_{sin}}({{t}_{1}})\xrightarrow{{{\mathit{\boldsymbol{H}}}_{r}}{{t}_{2}}}{{\mathit{\boldsymbol{\rho }}}_{sin}}({{t}_{1}},{{t}_{2}}) \\ \end{align} \right. $ |
(5)FID信号的检测:
| $ \left\{ \begin{align} & Tr\left\{ {\mathit{\boldsymbol{I}}^{\bf{+}}}\left[ {{\mathit{\boldsymbol{\rho}} }_{cos}}({{t}_{1}}, {{t}_{2}}) \right] \right\}\exp (-{{{t}_{1}}}/{{{T}_{1}}}\;)\exp (-{{{t}_{2}}}/{{{T}_{2}}}\;)\xrightarrow{{}}FI{{D}_{\cos }}({{t}_{1}}, {{t}_{2}}) \\ & Tr\left\{ {\mathit{\boldsymbol{I}}^{\bf{+}}}\left[ {{\mathit{\boldsymbol{\rho}} }_{sin}}({{t}_{1}}, {{t}_{2}}) \right] \right\}\exp (-{{{t}_{1}}}/{{{T}_{1}}}\;)\exp (-{{{t}_{2}}}/{{{T}_{2}}}\;)\xrightarrow{{}}FI{{D}_{\sin }}({{t}_{1}}, {{t}_{2}}) \\ \end{align} \right. $ |
(6)循环采样:演化期t1从0开始,每完成一次检测期t2的采样,t1时间递增t1/m,重复步骤(3)~(5),直到完成采样矩阵.
(7)NMR频域信号的产生:采用States方法对采样矩阵做以下处理,其中fft表示傅里叶变换.
| $ \left\{ \begin{align} & S({{t}_{1}}, {{\omega }_{2}})=\operatorname{Re}\left\{ fft\left[ FI{{D}_{\cos }}({{t}_{1}}, {{t}_{2}}) \right] \right\}\text{+i Re}\left\{ fft\left[ FI{{D}_{\sin }}({{t}_{1}}, {{t}_{2}}) \right] \right\} \\ & S({{\omega }_{1}}, {{\omega }_{2}})=\operatorname{Re}\left\{ fft\left[ S({{t}_{1}}, {{\omega }_{2}}) \right] \right\} \\ \end{align} \right. $ |
(8)分别绘制数据点阵的二维堆积图与等高线图,实现HSQC实验的谱图模拟.
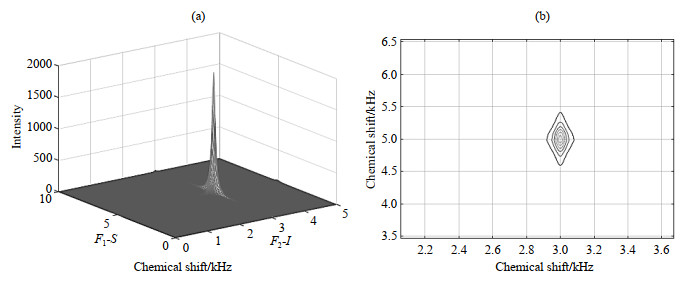
2 结果与讨论 2.1 IS体系的模拟自旋1/2的IS体系的HSQC模拟实验,设置数据点阵为1 024×512;采样时间t2=102.4 ms;演化期t1=10.24 ms;信号衰减系数T1=1 ms、T2=5 ms;时延参数τ选择模拟方案中设定的默认项.输入ωI=3 kHz、ωS=5 kHz、JIS=100 Hz,得到HSQC模拟谱图如图 4所示.图 4(a)是HSQC二维堆积谱图,图 4(b)是HSQC二维等高线谱图.根据图谱信息显示,IS基团的特征峰位于(3 kHz,5 kHz)处,模拟结果与理论输入一致.
|
图 4 IS体系HSQC模拟的谱图:(a)二维堆积图;(b)二维等高线图 Fig. 4 The simulation of HSQC spectrum for IS ensemble: (a) 2D stacked plot; (b) 2D contour plot |
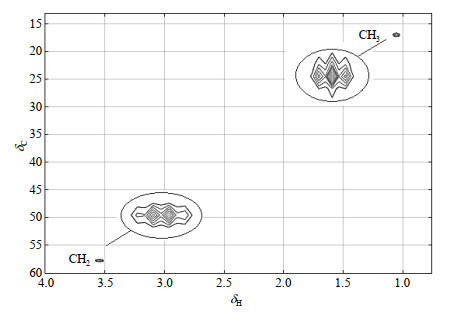
在双核体系HSQC实验计算模拟的框架上,通过设置多核体系的自旋算符和哈密顿函数,可实现多核体系的模拟.以乙醇(C2H6O)分子为例,生物磁共振数据库(BMRB)中乙醇的1H-13C HSQC实验谱图[23]如图 5所示,实验仪器为Bruker DMX-400MHz.其中CH2的化学位移为δH 3.544、δC 57.720,CH3的化学位移为δH 1.057、δC 17.063.谱图中小方框内为对应区域放大的特征峰信号,可以看到特征峰发生裂分.
在HSQC模拟中乙醇分子的CH2、CH3基团组成七核体系,该体系自旋算符的求解方程如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{I}}_{1m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}}\\ {\mathit{\boldsymbol{I}}_{2m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}}\\ {\mathit{\boldsymbol{I}}_{3m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}}\\ {\mathit{\boldsymbol{I}}_{4m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}}\\ {\mathit{\boldsymbol{I}}_{5m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}}\\ {\mathit{\boldsymbol{S}}_{1m}} = {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}}\\ {\mathit{\boldsymbol{S}}_{2m}} = {\mathit{\boldsymbol{I}}_{m(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \otimes {\mathit{\boldsymbol{E}}_{(2 \times 2)}} \end{array} \right.\begin{array}{*{20}{c}} \begin{array}{l} \\ \end{array}&{(m = [x, y, z])} \end{array} $ | (20) |
其中m表示坐标系中x、y、z各轴方向;I、S分别表示H、C的自旋算符,I的数字下标1~3分别标记CH3基团中不同的H,数字下标4~5标记CH2基团中的H,S的数字下标1~2分别标记CH2、CH3基团中的C.
该七核体系的哈密顿函数可表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{{ H}}} = {\omega _1}({\mathit{\boldsymbol{I}}_{1z}} + {\mathit{\boldsymbol{I}}_{2z}} + {\mathit{\boldsymbol{I}}_{3z}}) + {\omega _2}({\mathit{\boldsymbol{I}}_{4z}} + {\mathit{\boldsymbol{I}}_{5z}}) + {\omega _{1s}}{\mathit{\boldsymbol{S}}_{1z}} + {\omega _{2s}}{\mathit{\boldsymbol{S}}_{2z}}\\ \;\;\;\; + 2\pi {J_{1S}}({\mathit{\boldsymbol{I}}_{1z}}{\mathit{\boldsymbol{S}}_{1z}} + {\mathit{\boldsymbol{I}}_{2z}}{\mathit{\boldsymbol{S}}_{2z}} + {\mathit{\boldsymbol{I}}_{3z}}{\mathit{\boldsymbol{S}}_{3z}}) + 2\pi {J_{2S}}({\mathit{\boldsymbol{I}}_{4z}}{\mathit{\boldsymbol{S}}_{2z}} + {\mathit{\boldsymbol{I}}_{5z}}{\mathit{\boldsymbol{S}}_{2z}})\\ \;\;\;\;+ 2\pi J({\mathit{\boldsymbol{I}}_{1z}}{\mathit{\boldsymbol{I}}_{4z}} + {\mathit{\boldsymbol{I}}_{2z}}{\mathit{\boldsymbol{I}}_{4z}} + {\mathit{\boldsymbol{I}}_{3z}}{\mathit{\boldsymbol{I}}_{4z}} + {\mathit{\boldsymbol{I}}_{1z}}{\mathit{\boldsymbol{I}}_{5z}} + {\mathit{\boldsymbol{I}}_{2z}}{\mathit{\boldsymbol{I}}_{5z}} + {\mathit{\boldsymbol{I}}_{3z}}{\mathit{\boldsymbol{I}}_{5z}}) \end{array} $ | (21) |
其中,ω1、ω2分别表示CH2、CH3基团中质了化学位移的对应频率,ω1s、ω2s分别表示CH2、CH3基团中13C化学位移的对应频率;J1s、J2s分别表示CH2、CH3基团中C-H的耦合常数;J表示不同基团中质子之间的耦合常数.
参考实验数据调整模拟参数为:数据矩阵为1 024×512;采样时间t2=276 ms;演化期t1=40.96 ms;信号衰减系数T1=18 ms,T2=90 ms;时延参数τ=1.72 ms.CH2化学位移的对应频率(ωH=1.418 kHz,ωC=5.807 kHz),CH3化学位移的对应频率(ωH=0.423 kHz,ωC=1.717 kHz);耦合常数[24]设置为JCH(CH2)=140.2 Hz,JCH(CH3)=126.9 Hz,JHH=6.9 Hz.
执行模拟后得到的频谱信号如图 6所示,CH2特征峰位于δH 3.54、δC 57.71,CH3特征峰位于δH 1.05、δC 17.06,模拟结果与实验谱图一致.图中圆圈内的信号表示放大的特征峰,其中CH3受到CH2中的两个质子的耦合作用,对应的特征峰裂分为三重峰;CH2受到CH3中的三个质子的耦合作用,对应的特征峰裂分为四重峰.由于氢核之间耦合作用很小,在模拟结果中特征峰只是发生轻微的裂分,但相比于实验HSQC谱,模拟频谱图中特征峰裂分的效果比较明显.
|
图 6 乙醇分子的HSQC模拟谱图 Fig. 6 The simulated HSQC spectrum of ethanol |
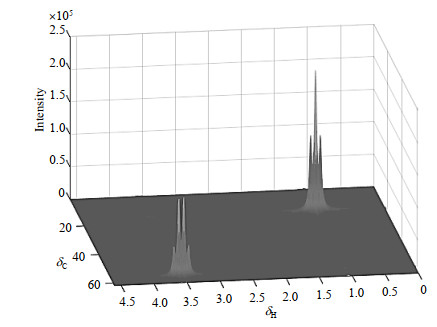
放大H-H耦合作用的效果,模拟产生的二维堆积图如图 7所示,图中CH2基团对应特征峰产生4个裂分,强度之比为1:3:3:1;CH3基团对应特征峰产生3个裂分,强度之比为1:2:1;模拟的结果符合液体NMR中耦合作用产生的频谱裂分规律.
|
图 7 乙醇分子的HSQC模拟中放大耦合作用的二维堆积图 Fig. 7 The 2D stacked plot of HSQC simulation with amplified coupling of ethanol |
本文基于NMR的量子力学原理建立了HSQC实验的计算模型,可根据输入的实验参数,将IS自旋体系所涉及的哈密顿量都写入密度矩阵演化方程中,在脉冲作用下自旋体系从初态到终态自行演化,详细记录密度矩阵在各个脉冲节点的状态,并对信号进行采样和傅里叶变换,在Matlab软件平台进行数值模拟得到HSQC谱图,谱图显示的结果与理论输入相符合.密度矩阵演化的计算过程都由计算机执行,能直观反应理论推导的效果.基于双核体系的模拟计算框架,本文通过设置多核自旋体系的相关参数,模拟了乙醇分子HSQC谱图,与实验HSQC谱图一致.
本文基于化学位移和J耦合作用建立液体NMR HSQC实验的计算模型,模型中暂未考虑NMR中其他相互作用和相关因素,如弛豫效应对HSQC实验的影响,尚未能对HSQC实验实现精确模拟,而且多核体系的计算效率有待优化.尽管如此,从量子计算角度建立理论模型来模拟NMR实验,能够实现难以直接求解的多核自旋体系的模拟,对辅助分析和研究HSQC实验都具有重要意义.
致谢 姚叶锋致谢“华东师范大学微观磁共振平台”,李鹏和何培忠致谢国家自然科学基金重点项目(No.81830052)、上海市分子影像学重点实验室建设项目(18DZ2260400)、上海市Ⅱ类高原学科建设计划(2018-2020)和国家重大科学仪器设备开发专项(2013YQ170463).
利益冲突 无
附件材料附录
IS 体系和 I2S 体系 HSQC 模拟视频
| [1] | ERNST R R, BODENHAUSEN G, WOKAUN A. Principles of nuclear magnetic resonance in one and two dimensions[M]. London: Oxford Science Publications, Clarendon Press, 1987. |
| [2] |
ZHANG M G, FENG X H, YU S T, et al. Spectral analysis and structural elucidation of besifloxacin hydrochloride[J].
Chinese J Magn Reson, 2018, 35(3): 374-384.
张明光, 冯小虎, 于水涛, 等. 盐酸贝西沙星的波谱学数据与结构确证[J]. 波谱学杂志, 2018, 35(3): 374-384. |
| [3] | SAMI H, MERJA M, TOIKKA P, et al. Quantitative 2D HSQC (Q-HSQC) via suppression of J-dependence of polarization transfer in NMR spectroscopy: application to wood lignin[J]. J Am Chem Soc, 2003, 125: 4362-4367. DOI: 10.1021/ja029035k. |
| [4] | 王乃兴. 核磁共振谱学: 在有机化学中的应用[M]. 第三版. 北京: 化学工业出版社, 2015. |
| [5] | DODDRELL D M, PEGG D T, BENDALL M R. Distortionless enhancement of NMR signals by polarization transfer[J]. J Magn Reson, 1982, 48(2): 323-327. |
| [6] | MEAKIN P, JESSON J P. Computer simulation of multipulse and Fourier transform NMR experiments. I. Simulations using the Bloch equations[J]. J Magn Reson, 1973, 10(3): 290-315. |
| [7] |
WANG H Z, WANG S L, HU B W, et al. A virtual NMR spectrometer based on numerical computational simulations[J].
Chinese J Magn Reson, 2019, 36(3): 288-297.
汪红志, 王申林, 胡炳文, 等. 基于数值计算模拟的仿真核磁共振波谱仪开发[J]. 波谱学杂志, 2019, 36(3): 288-297. |
| [8] | SMITH S A, LEVANTE T O, ERNST R R, et al. Computer simulations in magnetic resonance. An object-oriented programming approach[J]. J Magn Reson, 1994, 106(1): 75-105. DOI: 10.1006/jmra.1994.1008. |
| [9] | BAK M, RASMUSSEN J T, NIELSEN N C. SIMPSON: A general simulation program for solid-state NMR spectroscopy[J]. J Magn Reson, 2000, 147(2): 296-330. DOI: 10.1006/jmre.2000.2179. |
| [10] | VESHTORT M, GRIFFIN R G. SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments[J]. J Magn Reson, 2006, 178(2): 248-282. DOI: 10.1016/j.jmr.2005.07.018. |
| [11] | NICHOLAS P, FUSHMAN D, RUCHINSKY V, et al. The virtual NMR spectrometer: A computer program for efficient simulation of NMR experiments involving pulsed field gradients[J]. J Magn Reson, 2000, 145(2): 262-275. DOI: 10.1006/jmre.2000.2108. |
| [12] | HOGBEN H, KRZYSTYNIAK M, CHARNOCK G, et al. Spinach-a software library for simulation of spin dynamics in large spin systems[J]. J Magn Reson, 2011, 208(2): 179-194. DOI: 10.1016/j.jmr.2010.11.008. |
| [13] | KUPROV I. Large-scale NMR simulations in liquid state: A tutorial (Article)[J]. Magn Reson Chem, 2018, 56(6): 415-437. DOI: 10.1002/mrc.4660. |
| [14] | D'ALESSANDRO D. Introduction to quantum control and dynamics[M]. London: Chapman&Hall/CRC, 2008. |
| [15] | LEVITT M H. Spin dynamics: basics of nuclear magnetic resonance[M]. Chichester: John Wiley&Sons Ltd, 2008. |
| [16] | GORDON S, RULE T. Fundamentals of protein NMR spectroscopy[M]. Berlin: Springer, Dordrecht, 2006. |
| [17] | 赵天增. 核磁共振二维谱[M]. 北京: 化学工业出版社, 2017. |
| [18] | PRAVAT K, MANDAL, ANANYA M. A comprehensive discussion of HSQC and HMQC pulse sequences[J]. Concept Magn Reson A, 2004, 20(1): 1-23. |
| [19] | 杨立. 二维核磁共振简明原理及图谱解析[M]. 兰州: 兰州大学出版社, 1996. |
| [20] | HOMANS S W. A dictionary of concepts in NMR[M]. London: Oxford Science Publications, Clarendon Press, 1995. |
| [21] | KAREN D L, MANUEL A. The heteronuclear single-quantum correlation (HSQC) experiment: vectors versus product operators[J]. J Chem Educ, 2015, 92(3): 482-487. DOI: 10.1021/ed500575p. |
| [22] | JAY H B. Advances and applications of dynamic-angle spinning nuclear magnetic resonance spectroscopy[D]. Berkeley: University of California, 1993. |
| [23] | https://bmrb.io/metabolomics/mol_summary/show_data.php?id=bmse000297[OL]. |
| [24] |
WANG Y. Theoretical study on nuclear spin-spin coupling constants of C-H bonds[J].
Journal of Sichuan University of Science&Engineering (Natural Science Edition), 2009, 22(3): 57-59.
王莹. C-H键核自旋耦合常数的理论研究[J]. 四川理工学院学报(自然科学版), 2009, 22(3): 57-59. |
 2021, Vol. 38
2021, Vol. 38