2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
传统的梯度(Gradient)线圈和匀场(Shim)线圈是由多个Maxwell线圈或Golay线圈组合而成[1, 2],目前主要是利用目标场法[3, 4]和流函数[5]等方法进行设计.根据Maxwell方程,静态磁场可用球面谐波(Spherical Harmonic,SH)函数表示[6],即由一组无穷正交球谐函数项组成.线圈的次数和阶数对应SH函数的次数和阶数,本文称这类线圈为常规线圈或传统线圈.常规线圈之间相互独立,将这些线圈安装在空间有限的扫描孔内,用于产生线性梯度场G,并进行有源匀场,即改善主磁场B0的均匀性.线圈设计完成后,产生的磁场形态仅与电流呈正比,不能灵活改变磁场形态;受线圈个数和效率的限制,也不可能实现无穷级数和无振幅约束的建模[7].另外,随着SH函数次数和阶数的增加,线圈结构变得越来越复杂,占用空间也越来越多.此外,对于磁场均匀性要求较高的场合,如空气-组织交界处磁化率变化明显的地方,常规线圈不能有效地实现高阶局部磁场的补偿[8];对于非线性的空间编码磁场(Spatial Encoding Magnetic Field,SEM),无法灵活产生非线性场,则可能无法满足新型磁共振成像(Magnetic Resonance Imaging,MRI)技术的需求.在超高场环境下,梯度线圈和匀场线圈距离太近很容易产生耦合现象[9].MRI需要在磁场中心某个球形区域(Diameter of Spherical Volume,DSV)内产生满足要求的磁场.常规线圈在DSV内产生的磁场不能灵活跟随目标体位置的变化而变化.因此为满足MRI需求,需要设计较大范围的DSV.
矩阵梯度线圈(Matrix Gradient Coil)可以弥补常规线圈的不足.理论上,只需使用一组矩阵梯度线圈即可产生简单和/或复杂的磁场[10].本文对矩阵梯度线圈研究现状进行了介绍,主要包括其结构、功能和应用等,有助于我国研究人员进一步了解该技术.
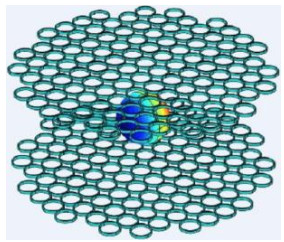
1 矩阵梯度线圈概念及特性矩阵梯度线圈由一组通用的、位置固定的线圈组成,每个小线圈称为一个线圈元素[11-14].由于线圈元素数量较多,可称之为多线圈(Multi Coil,MC)[11];又因其分布呈矩阵或阵列状,也可称之为矩阵梯度线圈[15, 16]或阵列(Arrays)[17]等,而本文选择称之为矩阵梯度线圈或MC线圈,其代表性结构如图 1所示.图 1(a)和1(b)中的线圈元素形状分别为圆形[11]和矩形[15].通过对每个线圈元素独立控制,产生一组非正交磁场,将这些磁场叠加求和,合成场即为MC线圈产生的磁场[12].
|
图 1 MC线圈的代表性结构. (a)线圈元素为圆形线圈[11];(b)线圈元素为矩形线圈[15] Fig. 1 Typical structures of MC coils. (a) Circular coil[11]; (b) Rectangular coil[15] |
本文根据MC线圈结构及其产生磁场原理,总结了其主要特性.
(1) MC线圈产生磁场的灵活性较强
通过优化MC线圈的各个元素电流,可以产生多样化磁场,或灵活改变磁场形态,从而满足梯度、高阶匀场和非线性编码等需求.MC线圈还可以针对切片位置产生相应的梯度[18],缩小DSV范围,为不同的成像区域提供灵活、准确的磁场[14],如非中心位置.
(2) MC线圈的鲁棒性较好
线圈的鲁棒性是指维持产生原磁场的能力.常规线圈导线呈串联关系,任意一段出现故障,线圈将停止工作,从而影响该线圈对应的梯度或匀场功能.MC线圈元素之间相互独立,产生的磁场为各个元素磁场之和.因此,当某些线圈元素产生故障时,不影响其他元素的工作,具有维持产生原有磁场的能力,提高了线圈的鲁棒性和可靠性,但其维持程度需要继续研究.
(3) MC线圈的安全性能较高
梯度场强度随时间的变化,可诱导产生感应电场,引起周围神经刺激(Peripheral Nerve Stimulation,PNS)(如刺痛或叩击感)、骨骼肌细胞刺激、磁致光幻视,甚至心脏兴奋或室颤等安全问题[19, 20],特别是在因提高梯度强度和线性度而需要使用高电压和高电流的情况下.所以,梯度系统性能更主要是受到安全问题的限制,而不仅仅是技术和经济的限制[21].线圈电感值影响梯度场切换速度和成像时间.常规线圈电感值较大,需要使用较高的电压和电流进行驱动,不仅存在电压、电流上升时间长,梯度切换速度慢,成像时间长等问题,安全性也有待考量.而MC线圈元素的电感值较小,使用低压电流放大器即可实现对线圈的驱动以及电流的快速切换[22],使得MC线圈更适合用于动态匀场[12].在需要产生强度较高的梯度场时,可通过增加线圈匝数来实现.
MRI和光谱成像等通常是建立在多切片或多体素基础之上的,MC线圈展现出较高的灵活性,其产生的磁场并不局限于轴向切片,还可以满足其他切片方向磁场的需求[12, 22].因此,MC线圈适用于对磁场准确性要求较高的场合,例如功能MRI,用于局部高分辨率成像的SEM,如PatLoc(Parallel Imaging Technique Using Localized Gradients)或ExLoc(Excitation and Geometrically Matched Local Encoding)[22].用于动态多线圈匀场(如对脊柱、乳腺、前列腺或四肢等局部进行成像的应用)等场合.但是,MC线圈元素数量较多、距离较近、磁场非正交、线圈元素之间相互耦合[23],导致其整体工作效率比常规线圈低;每个线圈元素都需要使用一个梯度放大器进行驱动,增加了线圈控制和驱动电路设计的难度;由MC线圈诱发的涡流问题[24]也亟待研究.MC线圈的优势和劣势为MC线圈的发展带来了机遇和挑战.
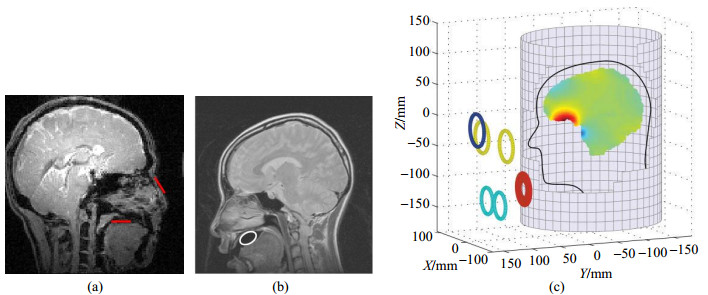
2 MC线圈的前期研究在形成MC线圈概念和结构之前,已有研究人员利用若干个局部线圈实现梯度、匀场和非线性编码等功能,为后续MC线圈的发展奠定了理论和实验基础.2004年,为改善下额叶皮层(Inferior Frontal Cortex,IFC)区域成像时磁场的均匀性,Wong等[25]将局部匀场线圈放置于被试口腔内部和鼻子外部上方[如图 2(a)].2005年,为改善下额叶(Inferior Portion of the Frontal Lobe)区域成像时磁场的均匀性,Hsu等[26]将局部匀场线圈放置于被试口腔内部,如图 2(b)所示.两者均实现了较好的匀场效果.
|
图 2 早期应用研究中,局部匀场线圈的放置位置. (a)口腔内部和鼻子外部上方[25];(b)口腔内部[26];(c)面罩外部[27] Fig. 2 Locations of shimming coil during the initial application research. (a) Intra-oral position and external position over the nose[25]; (b) Intra-oral position[26]; (c) Outside of the facial mask[27] |
在体内放置匀场线圈可能会降低患者的舒适度,2010年,Juchem等[27]在面罩外部安装直流线圈,减小或消除人脑额叶皮层处磁场的不均匀性,如图 2(c)所示.
多线圈组合还可以应用于其他场合.四川大学刘冀成等[28]使用半球形和平面形两种磁聚焦线圈阵列很好地实现了电磁聚焦功能,该阵列还具备聚焦至多个非中心点靶目标的能力.Gleich等[21]使用三组线圈产生三个正交均匀场.Hennig等[29]使用八边形梯度系统产生非线性梯度场等.Lin等[30]使用8个圆形梯度线圈生成线性和非线性SEM.
3 MC线圈的研究现状本文根据MC线圈的结构、功能和应用等,对其研究现状进行介绍.
3.1 经典结构的MC线圈经典结构的MC线圈是指线圈元素的形状(可为圆形、矩形等形状)、大小等均一致,使用多匝导线绕制而成,分布在圆柱体或平面表面,可分别实现梯度和匀场功能,或同时实现这两个功能,是最早提出并应用于成像的结构之一.
2010年,Juchem等[11]首次使用多线圈技术实现小鼠头部的线性成像[31][图 1(a)],并对线性梯度和2~3阶SH磁场进行了研究,证明MC线圈可以生成任意磁场形状,但没有达到传统梯度水平.辐射成像中,X梯度磁场强度为47 mT/m.MC线圈位于射频(Radio Frequency,RF)线圈和目标场之间,影响RF线圈灵敏度和效率.2010年,Wintzheimer等[15]仿真并制作了一个双平面矩阵梯度系统,如图 1(b)所示.该结构可同时实现梯度和匀场两个功能,产生的X梯度磁场强度为23.3 mT/m.
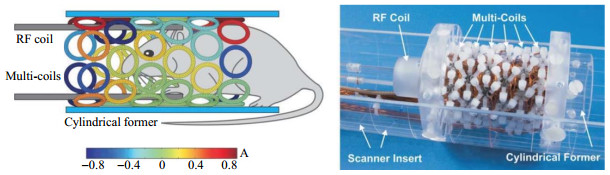
为提高RF线圈的灵敏度和效率,Juchem等[7, 32, 33]将RF线圈放置于MC线圈和目标场之间,如图 3所示,分别实现了动态多线圈匀场、对小鼠大脑区域的空间选择和产生所有1~4阶SH函数项.其中,线性梯度强度为94 mT/m;线性梯度场效率与最先进的SH梯度线圈具有相同数量级,但仍然较小.随着组合SH项的增加,MC线圈表现的性能越来越好.但由于位于RF线圈外部,MC线圈效率降低了.
|
图 3 RF线圈放置于MC线圈和目标场之间[7]. 工程设计图(左)和实验装置图(右) Fig. 3 RF coil is placed between MC coil and the target field[7]. Technical design drawing (left) and experimental setup drawing (right) |
为尽量减少与射频线圈的相互作用,Juchem等[12]将MC线圈分为上、下两部分,RF信号从中间穿过[12],如图 4所示.该结构可用于消除人脑中大部分的不均匀磁场,一定程度上减小RF信号畸变和信噪比损失,但对匀场性能产生了一定影响.
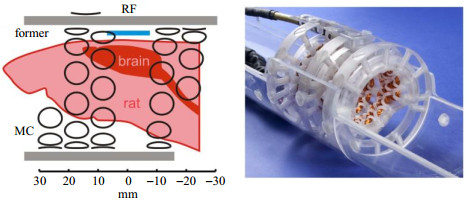
为进一步减少MC线圈和RF线圈的相互作用,Juchem等[31]将匀场直流线圈和表面收发RF线圈集成到同一组线圈中,如图 5所示.应用动态多线圈(Dynamic Multi-Coil Technique,DYNAMITE)匀场技术对活体大鼠脑部进行成像,并与3阶SH匀场进行比较,认为DYNAMITE是目前对大鼠体内整体磁场均匀化最有效的方法.该结构避免了MC线圈和RF线圈的重叠和直接接近,从而防止两者相互作用引起的RF线圈收发效率的降低.
|
图 5 集成的MC/RF结构[31]. 工程设计图(左)和实验装置图(右) Fig. 5 Integrated MC/RF setup[31]. Technical design drawing (left) and experimental setup drawing (right) |
Juchem等[18]继续利用MC线圈首次实现MRI所需的全部梯度场.获得的图像保真度表明,使用常规梯度线圈和DYNAMITE产生的效果几乎相同.Topfer等[23]针对人体脊髓成像所需的磁场进行校正,将非正交线圈放置在患者身体下面,靠近受试者脊柱,可以很好地提高磁场均匀性.Jia等[34]针对圆柱体表面具有大量线圈的结构进行研究,并提出一种性能评估的方法,为确定径向和纵向线圈个数提供理论支撑.Aghaeifar等[35]设计了一种用于人脑的16通道MC匀场装置.该装置和扫描仪内置匀场线圈一起实现了1阶动态匀场,减轻了超高场下B0场的严重畸变,改善了人类大脑成像和光谱质量.Rudrapatna等[36]使用两种不同的DYNAMITE方法分别同时实现编码和匀场功能,验证MC线圈可以实现基于傅里叶的k空间编码和回波平面成像(Echo Planar Imaging,EPI).
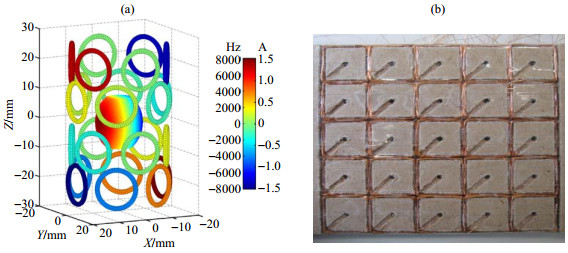
2016年,中国科学院电工研究所杨文晖课题组[37, 38]对矩阵梯度线圈展开研究:针对纵向、横向和平板、圆柱形梯度阵列进行讨论,并对不同形状的矩阵线圈进行探索.他们还使用粒子群与遗传算法对开放式永磁型MRI系统的矩阵梯度线圈进行优化设计[39],如图 6所示,验证了矩阵梯度电流计算方法的有效性.
2018年,中国科学院苏州生物医学工程技术研究所徐雅洁等[40]利用阵列线圈对Halbach磁体进行匀场,选择马鞍形线圈作为阵列线圈单元.该结构能够有效地产生X、Z2、X2-Y2和X+XZ 4组SH分量,可应用于基于Halbach磁体的小型化磁共振系统中.
3.2 基于流函数设计的MC线圈基于流函数设计的MC线圈是指线圈元素形状是根据流函数计算得到的,然后将其分布在圆柱体表面,实现梯度和匀场功能.
2014年,While等[17]提出了一种非规则阵列线圈的设计方法,结合低阶SH和MC线圈匀场的优点,利用流函数优化线圈元素几何形状,如图 7所示.该方法使用两层MC线圈,分别产生1阶和2阶SH项以提高其性能.其中,1阶和2阶项强度分别为5 mT/m和5 mT/m2.当单个线圈的驱动电流峰值受到限制时,该结构的优势比较明显.但是,内层线圈会对外层线圈匀场效果造成影响,且由于设计参数个数的增加,该方法扩展到更高阶时可能会导致计算困难.

|
图 7 一个象限中6个线圈绕组分布[17]. (a) 1阶复合阵列;(b) 2阶复合阵列 Fig. 7 Coil windings for the six subregions in one quadrant[17]. (a) First-order composite array; (b) Second-order composite array |
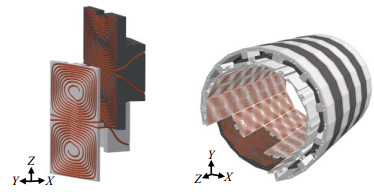
2015年,Jia等[16, 22]基于流函数提出一种主动屏蔽矩阵梯度线圈的优化设计方法,增加对屏蔽层的设计,旨在提高梯度线圈性能,降低涡流影响,如图 8所示.随后,Littin等[41]将该结构缩小到头部尺寸进行实验验证,可以实现24 mT/m~78 mT/m之间的梯度强度,涡流小于1%.
|
图 8 优化的线圈元素导线路径和矩阵梯度线圈效果图[22] Fig. 8 Optimized coil element wire path and matrix gradient coil rendering[22] |
当MC线圈元素更多、更接近目标体时,会增加其与RF线圈之间的相互影响,造成空间关系紧张[42].为解决上述问题,经典结构已提出一些改进方法.本节将介绍另一种改进方法,即将匀场和RF功能集成到同一线圈,通过在RF交流回路中增加扼流线圈来实现.扼流线圈的作用是给匀场提供直流回路,这种结构被称为iPRES(Integrated Parallel Reception, Excitation, and Shimming)[43],交流/直流(Alternating Current/Direct Currents,AC/DC)[42],或RF-shim array[44]等.其基本理论依据为:不同频率的电流可以在同一电路中独立共存,它们之间没有电磁干扰[43].这种同时实现RF功能和B0匀场功能的MC线圈(简称为RF-shim线圈),可以提高信噪比和匀场性能[45];但也有文献[46]认为,该结构增加了扼流线圈,引起效率和信噪比的损失.
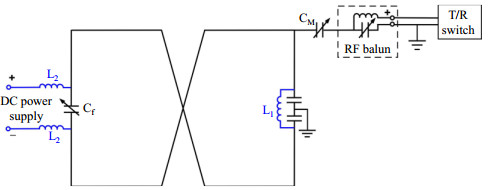
2013年,Han等[43]第一次提出将RF并行激励/接收线圈(AC交流)和B0匀场线圈(DC直流)集成至同一线圈的概念,即iPRES,电路原理如图 9所示.该电路能同时流入交流和直流,不会影响RF线圈特性,包括线圈方向、几何形状以及每个线圈元素的RF电流属性,但匀场性能与RF线圈结构相关.扼流线圈的引入,增加了电路结构的复杂程度.
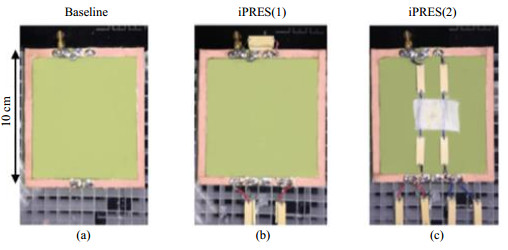
为了提高iPRES匀场性能,2017年,Darnell等[47]在RF线圈中设计多条独立直流回路,该方法被称为iPRES(N),N表示每个RF线圈中直流回路个数(图 10).由于RF线圈面积有限,划分的直流回路越多,电路越复杂,使用的直流电源数量也越多.独立直流回路个数与磁场效果之间的关系还需进一步研究.
|
图 10 射频线圈[47].(a)基础线圈;(b) iPRES(1);(c) iPRES(2) Fig. 10 RF coil[47].(a) Baseline; (b) iPRES(1); (c) iPRES(2) |
Rudrapatna等[36]和Stockmann等[44]将RF-shim线圈应用于脑部成像.头盔型结构更接近人脑形状,离目标体更近,提高了匀场效率,节约了空间.Stockmann等[48]对头部线圈个数进行仿真和实验,结果表明32通道线圈的匀场性能可与3阶全局匀场和4阶切片优化匀场效果相媲美;128通道线圈可达到5阶或6阶SH匀场效果(除了离窦腔很近的切片).该文献认为MC线圈匀场性能主要受到通道数的限制,而不是通道中实际电流的限制.
2018年,Winkler等[46]提出两种将RF-shim电路分开的线圈结构 ,目的是最大限度减少两个系统之间的干扰,提高利用率.该结构没有引入扼流线圈,减少了额外损耗和设计难度,但却降低了电路的集成度.
2019年,浙江大学Gao等[45]利用集成的AC/DC阵列线圈(图 11)对猴子全脑进行成像,结果显示该结构可以较好地检测脑部激活效果,提高功能性成像质量.
2019年,Zhou等[8]设计并实现了一种匀场线圈阵列,使匀场线圈平面与相邻RF线圈平面相垂直,并验证了其垂直结构的匀场效果.
3.4 使用开关结构的MC线圈使用开关结构的MC线圈是指通过使用开关器件改变直流电流路径,增加其自由度,在保证匀场效果和性能的前提下,尽可能地减少直流电源(梯度放大器)的使用.
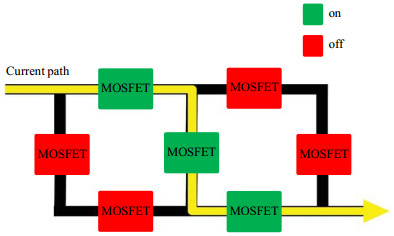
2014年,Harris等[10]结合MC线圈和金属-氧化物半导体场效应晶体管(Metal-Oxide-Semiconductor Field-Effect Transistor,MOSFET)开关特点,将线路设计成网格状,实现对圆柱体表面电流的动态自适应控制,提高了磁场均匀性,如图 12所示.该结构仅使用一个电流放大器即获得了高效率的匀场效果[49].整个电流路径都对目标场起作用,避免了MC线圈可能出现的效率损失[50].但该结构对开关器件具有依赖性:开关数量较少,网格较稀疏,匀场效果较差;开关数量较多,匀场效果较好,但增加了额外损耗和路径选择问题.
|
图 12 MOSFET处于开关两个状态时的电流流通路径[10] Fig. 12 Two separate current pathways depending on which MOSFETs are in the open or closed state[10] |
2017年,Darnell等[51]在iPRES(N)结构基础上增加微电机系统(Microelectromechanical Systems,MEMS)开关,只需一台直流电源即可实现对线圈元素中多条直流电路的驱动,该方法被称为iPRES(N)-A,如图 13所示.在保证射频和匀场功能的前提下,通过减少直流电源个数达到降低设计成本的目的.

|
图 13 RF线圈[51].(a)基础线圈;(b) iPRES(2)-A集成4个MEMS开关 Fig. 13 RF coil[51].(a) Baseline; (b) iPRES(2)-A integration with four MEMS switches |
2018年,Kroboth等[49]对梯度放大器个数和目标场性能之间的关系进行研究,在前期研究[16, 22, 41]基础上,为每个线圈元素配置一组桥式开关以增加直流电流路径的自由度.该方法结合MC线圈和开关器件的优点,针对目标场寻找一组线圈元素之间最佳的连接方式,减少了梯度放大器的使用.放大器个数的减少,在一定程度上降低了产生磁场的灵活性.
3.5 优化线圈结构的MC线圈优化线圈结构的MC线圈是指根据磁场性能,对线圈形状、位置、大小等参数进行优化,从而确定MC线圈结构.
2020年,Aghaeifar等[52]对32个矩形线圈的角度、轴向位置以及线圈尺寸进行优化,图 14(a)为多线圈初始状态,图 14(b)为优化后状态,图 14(c)根据优化结果制作的实验装置.将其应用于人脑匀场,在不增加局部线圈数量的前提下改善了匀场性能.考虑到优化后的线圈可能部分或全部重叠,重叠线圈在制作过程中被安装在不同的层.

|
图 14 圆柱表面线圈分布[52].(a)多线圈初始状态;(b)优化后状态;(c)根据优化结果制作的实验装置 Fig. 14 The distribution of coils on the surface of the cylinder[52].(a) Before multi-coil optimization; (b) After optimization; (c) Experimental setup according to the optimized result |
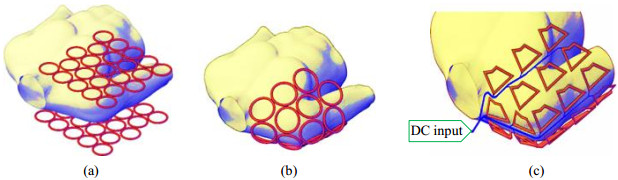
2019年,厦门大学Chen等[53]使用不规则形状的多线圈结构对肩关节进行匀场(图 15).基于遗传算法和模拟退火算法,将线圈形状作为优化目标进行研究.对于多边形多线圈结构,线圈边数越多,标准差越小,匀场效果越好;但当边数到达一定数量后,匀场效果将接近饱和.相同条件下,使用较少数量的不规则多线圈就能获得较多圆形线圈的匀场效果.
|
图 15 MC线圈模型[53].(a)平板结构;(b)肩关节结构;(c)优化线圈分布 Fig. 15 MC model[53].(a) Flat structure; (b) Shoulder structure; (c) Arrangement of optimized coils |
通过对上述MC线圈的发展现状进行介绍,可得到如下结论:MC线圈具有良好的灵活性,对其研究主要集中在改善MC线圈性能和应用方面.MC线圈性能的改善主要体现在磁场强度、均匀性、准确度和工作效率等.应用主要体现在对不同目标体的成像、动态匀场技术以及扩展MC线圈功能,即同时实现射频和匀场功能.目前,经典结构的MC线圈以及RF-shim线圈研究较多,优化线圈结构的MC线圈也已经开始研究.表 1对MC线圈主要结构特点、实现功能和在研国家进行了汇总.表 2对MC线圈主要优缺点进行了汇总.
| 表 1 MC线圈主要结构、实现功能和在研国家 Table 1 The main structure, implementation function and countries under research of MC coils |
| 表 2 不同类型MC线圈的主要优缺点 Table 2 Main advantages and disadvantages of MC coils |
由于圆柱体或平面表面有限,实际线圈个数也受到限制,导致MC线圈产生的磁场始终与目标磁场之间存在误差,该误差只能尽可能减小.而且受线圈间相互作用等因素的影响,MC线圈性能较低.在MC线圈实际应用方面,有关硬件支持的研究也相对较少.基于此,MC线圈的发展大体有以下三个方向.
(1) 关于MC线圈特性的研究
MC线圈具有良好的灵活性和较强的鲁棒性,但前提是拥有足够多的线圈元素产生足够多的基础磁场[11].实际应用中,线圈结构会对磁场产生影响.因此,需要更加重视对MC线圈的基础研究,分析线圈与磁场之间的关系,深入了解MC线圈特性,为磁场产生等提供理论基础.
(2) 关于MC线圈性能的研究
MC线圈可以弥补传统线圈中出现的问题,但其性能的优劣决定该线圈是否具有实际应用价值.MC线圈元素个数较多、距离较近,电流之间的相互作用会造成部分电能损耗,降低电流效率和磁场强度.因此,可以从提高磁场准确度、磁场强度,降低线圈电流和涡流,减小与目标体之间的距离等方面对MC线圈进行建模,以改善其性能.对于RF-shim线圈,其电路结构也是需要进一步研究的问题.为了扩大MC线圈应用范围,还可以对全身MC线圈进行研究.
(3) 关于MC线圈硬件装置的研究
MC线圈硬件装置不仅包括线圈制作,还包括电路结构、连接方式、驱动放大器、谱仪控制器、通讯设备、散热系统等.目前,已有文献[54]根据MC线圈的耦合作用对其驱动电路进行研究.当功率损耗较大时,需要提供充足的空气或水冷却,保障系统的安全.在保证磁场性能的同时,对放大器个数进行研究,以降低系统成本.实现MC线圈的模块化,便于对MC线圈的安装和维修.
5 总结"十三五"医疗器械科技创新专项规划[55]中明确指出,新一轮医疗器械科技革命的重要方向是"以人为本,以健康为中心".对于医学影像领域而言,则需更好地满足实时、快速、精确诊断以及术中精准治疗等应用需求.梯度线圈是产生梯度磁场的直接工具,如果没有高性能的硬件设备,仅改进软件技术,MRI技术的发展终将进入瓶颈期.从MC线圈基础研究出发,不仅仅是对梯度线圈的改进,更能使MRI技术焕发新生.MC线圈经历近十年的发展,已经成功地实现对小鼠、大鼠、猴脑和人脑等组织的成像,并取得了较好的效果,但距离临床应用还有很大的距离.本文通过对MC线圈的研究现状进行分析总结,并对其发展趋势进行讨论,希望有助于我国研究人员更全面地了解MC线圈及其特性,更好地实现其灵活性、准确性、安全性,缩小与国内外该技术的差距,并进一步推动MC线圈的基础研究和临床应用等提供参考价值.
利益冲突 无
| [1] | GOLAY, MARCEL J E. Field homogenizing coils for nuclear spin resonance instrumentation[J]. Rev Sci Instrum, 1958, 29(4): 313-315. DOI: 10.1063/1.1716184. |
| [2] | SIEBOLD H. Gradient field coils for MR imaging with high spectral purity[J]. IEEE T Magn, 1990, 26(2): 897-900. DOI: 10.1109/20.106462. |
| [3] | TURNER R. A target field approach to optimal coil design[J]. J Phys D Appl Phys, 1986, 19(8): L147-L151. DOI: 10.1088/0022-3727/19/8/001. |
| [4] | TURNER R. Minimum inductance coils[J]. J Phys E Sci Instrum, 1988, 21(10): 948-952. DOI: 10.1088/0022-3735/21/10/008. |
| [5] | PEEREN G N. Stream function approach for determining optimal surface currents[J]. J Comput Phys, 2003, 191(1): 305-321. DOI: 10.1016/S0021-9991(03)00320-6. |
| [6] | JUCHEM C, BIERL B M, SCHICK F, et al. Combined passive and active shimming for in vivo MR spectroscopy at high magnetic fields[J]. J Magn Reson, 2006, 183: 278-289. DOI: 10.1016/j.jmr.2006.09.002. |
| [7] | JUCHEM C, BROWN P B, NIXON T W, et al. Multicoil shimming of the mouse brain[J]. Magn Reson Med, 2011, 66(3): 893-900. DOI: 10.1002/mrm.22850. |
| [8] | ZHOU J Z, STOCKMANN J P, ARANGO N, et al. The orthogonal shim coil for 3T brain imaging[J]. Magn Reson Med, 2019, 83(1): 1-13. |
| [9] | WINKLER S A, SCHMITT F, LANDES H, et al. Gradient and shim technologies for ultra high field MRI[J]. Neuroimage, 2018, 168: 59-70. DOI: 10.1016/j.neuroimage.2016.11.033. |
| [10] | HARRIS C T, HANDLER W B, CHRONIK B A. A new approach to shimming: The dynamically controlled adaptive current network[J]. Magn Reson Med, 2014, 71(2): 859-869. DOI: 10.1002/mrm.24724. |
| [11] | JUCHEM C, NIXON T W, MCINTYRE S, et al. Magnetic field modeling with a set of individual localized coils[J]. J Magn Reson, 2010, 204(2): 281-289. DOI: 10.1016/j.jmr.2010.03.008. |
| [12] | JUCHEM C, NIXON T W, MCINTYRE S, et al. Dynamic multi-coil shimming of the human brain at 7 T[J]. J Magn Reson, 2011, 212(2): 280-288. DOI: 10.1016/j.jmr.2011.07.005. |
| [13] | JUCHEM C, NIXON T W, GRAAF R A D. Multi-coil imaging with algebraic reconstruction[C]//Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Australia, 2012. Abstract: 2545. |
| [14] | JUCHEM C, GRAAF R A D. The public multi-coil information (PUMCIN) policy[J]. Magn Reson Med, 2017, 78(5): 2042-2047. DOI: 10.1002/mrm.26558. |
| [15] | WINTZHEIMER S, DRIESSLE T, LEDWIG M, et al. A 50-channel matrix gradient system: a feasibility study[C]. In Proceedings of the joint annual meeting ISMRM-ESMRMB, Stockholm, Sweden, 2010: 3937 |
| [16] | JIA F, LITTIN S, LAYTON K J, et al. Design of a shielded coil element of a matrix gradient coil[C]//Proc Intl Soc Mag Reson Med, 23, 2015: 3091 |
| [17] | WHILE P T, KORVINK J G. Designing MR shim arrays with irregular coil geometry: theoretical considerations[J]. IEEE T Biomed Eng, 2014, 61(6): 1614-1620. DOI: 10.1109/TBME.2013.2293842. |
| [18] | JUCHEM C, NAHHASS O M, NIXON T W, et al. Multi-slice MRI with the dynamic multi-coil technique[J]. NMR Biomed, 2015, 28(11): 1526-1534. DOI: 10.1002/nbm.3414. |
| [19] |
YANG S G, LU X F, FU J Q, et al. Safety alert of high field or ultra-high field MRI for using[J].
Biomedical Engineering and Clinical Medicine, 2014, 18(1): 94-98.
杨述根, 陆笑非, 付家庆, 等. 高场或超高场MRI使用安全警示[J]. 生物医学工程与临床, 2014, 18(1): 94-98. |
| [20] |
TIAN J G, LIU M L, XIA Z F, et al. Safety of magnetic resonance imaging[J].
Chinese J Magn Reson, 2000, 17(6): 505-511.
田建广, 刘买利, 夏照帆, 等. 磁共振成像的安全性[J]. 波谱学杂志, 2000, 17(6): 505-511. |
| [21] | GLEICH B, WEIZENECKER J. Tomographic imaging using the nonlinear response of magnetic particles[J]. Nature, 2005, 435(7046): 1214-1217. DOI: 10.1038/nature03808. |
| [22] | JIA F, LITTIN S, LAYTON K J, et al. Design of a shielded coil element of a matrix gradient coil[J]. J Magn Reson, 2017, 281: 217-228. DOI: 10.1016/j.jmr.2017.06.006. |
| [23] | TOPFER R, STAREWICZ P, LO K M, et al. A 24-channel shim array for the human spinal cord: design, evaluation, and application[J]. Magn Reson Med, 2016, 76(5): 1604-1611. DOI: 10.1002/mrm.26354. |
| [24] |
SONG R, HE Y F, ZHANG B. A method for eddy current field measurement in permanent magnet magnetic resonance imaging systems[J].
Chinese J Magn Reson, 2018, 35(1): 52-59.
宋瑞, 何砚发, 张波. 一种永磁磁共振中磁体涡流场的测量方法[J]. 波谱学杂志, 2018, 35(1): 52-59. |
| [25] | WONG E C, MAZAHERI Y. Shimming of the inferior frontal cortex using an external local shim coil[J]. Proc Intl Soc Mag Reson Med, 2004, 11: 520. |
| [26] | HSU J J, GLOVER G H. Mitigation of susceptibility-induced signal loss in neuroimaging using localized shim coils[J]. Magn Reson Med, 2005, 53(2): 243-248. DOI: 10.1002/mrm.20365. |
| [27] | JUCHEM C, NIXON T W, MCINTYRE S, et al. Magnetic field homogenization of the human prefrontal cortex with a set of localized electrical coils[J]. Magn Reson Med, 2010, 63(1): 171-180. DOI: 10.1002/mrm.22164. |
| [28] |
LIU J C, HUANG K M, HU Y Y, et al. Design and field calculation of coil array for functional magnetic stimulation[J].
Space Medicine & Medical Engineering, 2004, 5: 365-369.
刘冀成, 黄卡玛, 胡雅毅, 等. 功能磁刺激线圈阵列设计与场分布计算[J]. 航天医学与医学工程, 2004, 5: 365-369. |
| [29] | HENNIG J, WELZ A M, SCHULTZ G, et al. Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study[J]. MAGMA, 2008, 21(1, 2): 5-14. DOI: 10.1007/s10334-008-0105-7. |
| [30] | LIN F H, WITZEL T, SCHULTZ G, et al. Reconstruction of MRI data encoded by multiple nonbijective curvilinear magnetic fields[J]. Magn Reson Med, 2012, 68(4): 1145-1156. DOI: 10.1002/mrm.24115. |
| [31] | JUCHEM C, HERMAN P, SANGANAHALLI B G, et al. DYNAmic Multi-coIl TEchnique (DYNAMITE) shimming of the rat brain at 11.7Tesla[J]. NMR Biomed, 2014, 27(8): 897-906. DOI: 10.1002/nbm.3133. |
| [32] | JUCHEM C, NIXON T W, BROWN P B, et al. Spatial selection through multi-coil magnetic field shaping[C]//Proceedings of the 19th Annual Meeting of ISMRM, Montreal, Canada: 2011. Abstract 385. |
| [33] | JUCHEM C, GREEN D, GRAAF R A D. Multi-coil magnetic field modeling[J]. J Magn Reson, 2013, 236C: 95-104. |
| [34] | JIA F, SCHULTZ G, TESTUD F, et al. Performance evaluation of matrix gradient coils[J]. MAGMA 29, 2016: 59-73. |
| [35] | AGHAEIFAR A, MIRKES C, BAUSE J, et al. Dynamic B0 shimming of the human brain at 9.4 T with a 16-channel multi-coil shim setup[J]. Magn Reson Med, 2018: 1-12. |
| [36] | RUDRAPATNA S, FLUERENBROCK F, NIXON T W, et al. Combined imaging and shimming with the dynamic multi-coil technique[J]. Magn Reson Med, 2019, 81(2): 1424-1433. DOI: 10.1002/mrm.27408. |
| [37] | 中国科学院电工研究所. 杨文晖, 王铮. 一种磁共振成像系统的梯度磁场产生方法及其装置: 中国. 105301536 A[P], 2016-02-03. |
| [38] | 中国科学院电工研究所. 杨文晖, 魏树峰, 王铮, 等. 磁共振成像系统的阵列梯度线圈: 中国. 107219480 A[P], 2017-09-29. |
| [39] |
WANG Q, WEI S F, WANG Z, et al. Design of matrix gradient coils with particle swarm optimization and the genetic algorithm[J].
Chinese J Magn Reson, 2019, 36(4): 463-471.
王强, 魏树峰, 王铮, 等. 基于粒子群与遗传算法的矩阵式梯度线圈优化设计[J]. 波谱学杂志, 2019, 36(4): 463-471. |
| [40] | 徐雅洁, 郁朋, 吴振洲, 等. Halbach阵列磁体中阵列线圈主动匀场技术[C]//2018第二十届全国波谱学学术年会会议论文摘要集. 中国物理学会波谱专业委员会, 2018: 326-327. |
| [41] | LITTIN S, JIA F, LAYTON K J, et al. Development and implementation of an 84-channel matrix gradient coil[J]. Magn Reson Med, 2018, 79(2): 1181-1191. DOI: 10.1002/mrm.26700. |
| [42] | STOCKMANN J P, WALD L L. In vivo B0 Field shimming methods for MRI at 7 T[J]. NeuroImage, 2017, 168: 71-87. |
| [43] | HAN H, SONG A W, TRUONG T K. Integrated parallel reception, excitation, and shimming (iPRES)[J]. Magn Reson Med, 2013, 70(1): 241-247. DOI: 10.1002/mrm.24766. |
| [44] | STOCKMANN J P, WITZEL T, BLAU J, et al. Combined shim-RF array for highly efficient shimming of the brain at 7 Tesla[C]//Proceedings of the 21st Annual Meeting of ISMRM; Salt Lake City, Utah, USA: 2013: 665. |
| [45] | GAO Y, MAREYAM A, SUN Y, et al. A 16-channel AC/DC array coil for anesthetized monkey whole-brain imaging at 7 T[J]. NeuroImage, 2020, 207: 116396. DOI: 10.1016/j.neuroimage.2019.116396. |
| [46] | WINKLER S A, WARR P A, STOCKMANN J P, et al. Comparison of new element designs for combined RF-shim arrays at 7 T[J]. Concepts Magn Reson B, 2018: e21364. |
| [47] | DARNELL D, TRUONG T K, SONG A W, et al. Integrated parallel reception, excitation, and shimming (iPRES) with multiple shim loops per RF coil element for improved B0 shimming[J]. Magn Reson Med, 2017, 77(5): 2077-2086. DOI: 10.1002/mrm.26267. |
| [48] | STOCKMANN J P, WITZEL T, KEIL B, et al. A 32-channel combined RF and B0 shim array for 3 T brain imaging[J]. Magn Reson Med, 2016, 75(1): 441-451. DOI: 10.1002/mrm.25587. |
| [49] | KROBOTH S, LAYTON K J, JIA F, et al. Optimization of coil element configurations for a matrix gradient coil[J]. IEEE T Med Imaging, 2018, 37(1): 284-292. DOI: 10.1109/TMI.2017.2743463. |
| [50] | STOCKMANN J P, WITZEL T, KEIL B, et al. A 32ch combined RF-shim brain array for efficient B0 shimming and RF reception at 3 T[C]//Proceedings of the 22nd Annual Meeting of ISMRM, Milan. Italy: 2014: 400. |
| [51] | DARELL D, MA Y X, WANG H Y, et al. Adaptive integrated parallel reception, excitation, and shimming (iPRES-A) with microelectromechanical systems switches[J]. Magn Reson Med, 2018, 80(1): 371-379. DOI: 10.1002/mrm.27007. |
| [52] | AGHAEIFAR A, ZHOU J Z, HEULE R, et al. A 32-channel multi-coil setup optimized for human brain shimming at 9.4 T[J]. Magn Reson Med, 2020, 83(2): 749-764. DOI: 10.1002/mrm.27929. |
| [53] | CHEN W J, CHEN J, SUN H J, et al. Simulation and analysis of irregular multicoil B0 shimming in C-type permanent magnets using genetic algorithm and simulated annealing[J]. Appl Magn Reson, 2019, 50(1-3): 227-242. DOI: 10.1007/s00723-018-1094-y. |
| [54] | ERTAN K, TARAGHINIA S, ATALAR E. Driving mutually coupled gradient array coils in magnetic resonance imaging[J]. Magn Reson Med, 2019, 82(3): 1187-1198. |
| [55] | "十三五"医疗器械科技创新专项规划. 科技部国科办社[2017] 44号. [2017.5.26]. http://www.most.gov.cn/tztg/201706/t20170612_133477.htm. |
 2021, Vol. 38
2021, Vol. 38