2. 中国科学院 苏州生物医学工程技术研究所, 江苏 苏州 215163;
3. 苏州大学附属儿童医院, 江苏 苏州 215000
2. Suzhou Institute of Biomedical Engineering and Technology, Chinese Academy of Science, Suzhou 215163, China;
3. Children's Hospital of Soochow University, Suzhou 215000, China
发育性髋关节脱位(developmental dysplasia of the hip,DDH)也称为发育性髋关节发育不良,是儿童骨科最常见的髋关节疾病.由于髋关节的发育是一个长期的动态过程,因此DDH治疗不仅与其严重程度相关,还取决于孩子的年龄[1].18个月以内的DDH患儿可以采用Pavlik吊带或者石膏固定来进行矫正,稍微严重的需要进行关节镜下清除术[2];18个月以上的DDH患儿可能需要髋臼周围截骨术、股骨截骨术[3]等治疗方法.随着患儿的年龄增大,病变程度更复杂、治疗难度更大,疗效也越差,也会过早的面临髋关节骨性关节炎、股骨头缺血性坏死(avascular necrosis,AVN)等风险,因而DDH的早诊断、早治疗非常重要.
DDH的治疗分为保守治疗和手术治疗,每种治疗方法都有各自的优缺点.对DDH治疗方式的选择应根据病儿的年龄、头臼发育状况等因素进行综合考虑,从而制定个体化方案[4].手术治疗方案的确定将大大影响治疗效果以及预后,但是依靠体格检查或者肉眼观测髋关节影像来制定手术方案存在困难.计算机断层扫描(computed tomography,CT)作为DDH的保留检查手段,因产生电离辐射,目前使用频率不高.磁共振成像(magnetic resonance imaging,MRI)技术与其相比,具有高分辨率、无电离辐射、骨骼和软组织区分能力高等优点,对髋臼发育不良的软骨及软组织诊断价值较高,因此成为目前DDH检查的重要影像学手段.
近年来出现了一些利用医学图像辅助诊断DDH的研究.Starr等[5]通过与超声和CT成像手段对比,探究了MRI对于DDH诊断的优势.Audenaert等[6]基于CT图像完成了自动股骨头球率评估用来制定在股骨髋臼撞击中凸轮变形的三维检测方法.Hareendranathan等[7]结合先验知识构建Random Walker网络结构,对磁共振图像中髋关节部分进行分割,以便为DDH患儿的诊断和治疗提供支持.国内也出现了利用医学影像技术开展DDH评价的相关报道.南昌大学第二附属医院通过MRI观察DDH患儿病变的髋关节和软骨髋臼是否存在过度前倾,测量正常儿童不同年龄软骨髋臼前倾度,分析其发育演变[8].苏州大学附属儿童医院针对63例经手术证实的DDH患者进行MRI成像,观察影响DDH复位的因素[9].
另外,也出现了一些通过形态学参数辅助诊断DDH的研究.Beltran等[10]通过手动测量髋关节磁共振图像三维重建模型的中心边缘角(center-edge angle,CEA)、股骨颈前倾角(femoral neck anteversion,FNA)等形态学参数,发现髋臼及股骨的形态学变化,为青少年DDH早期诊断及治疗提供了依据.Douira-Khomsi等[11]通过研究髋臼骨性以及软骨性的形态学参数来探究MRI在评估残余髋臼缺陷方面的作用及其对DDH手术方案的影响.Xia等[12]使用统计形状模型(statistical shape model,SSM)完成髋关节磁共振图像的自动分割与三维重建,用最小二乘法拟合股骨头与股骨颈最终实现了股骨头颈结构中立体α角的自动评估测定.Al-Bashir等[13]针对16名儿童的髋关节X射线图像,结合边缘检测、霍夫(Hough)变换等图像处理方法提出一种自动测量CEA的算法,辅助医师测量CEA,诊断DDH.国内第四军医大学基于髋关节的CT图像,利用PV(partial volume)算法分割髋臼等骨结构,对分割结果进行三维重建,实现对髋臼角(acetabular index,AI)、FNA等形态学参数的手动测量,为DDH的治疗提供计算机辅助诊断计划[14].解放军总医院和中国医科大学附属第二医院利用MRI研究了DDH患儿的AI与其实际髋臼状况的关系[15].但是至今尚未出现针对儿童DDH磁共振图像中多项形态学参数的自动测量及其定量评估.
在髋关节形态学参数中,CEA反映股骨头与髋臼的关系,可以作为股骨头在髋臼窝的稳定指数,并反映髋臼的发育程度[16];AI又称sharp角,主要反映髋臼与股骨头的包容程度,临床常以此诊断髋臼发育不良[17].AI和CEA是髋关节测量的重要参数,使髋关节疾病的诊断能够标准化、数字化.另外,FNA的异常是导致髋关节不稳定的因素之一,DDH患者术后常因为FNA的异常引起髋关节再次脱位[18],因此FNA的准确测量对保髋治疗或者全髋关节置换都至关重要.上述三项髋关节形态学参数共同作为髋关节发育状况监测的重要指标常用来作为判定DDH的重要标准[19].但对医生来说,这些参数的目测存在不准确性,且耗费时间精力,因此需要一个针对DDH疾病的自动化形态学定量评估方法.
本文面向DDH疾病的临床需求,基于DDH患儿的磁共振图像,建立DDH的髋关节三维模型,并设计针对CEA、AI以及FNA重要形态参数的自动测量算法,量化髋关节形态学参数,从而形成DDH磁共振形态学定量评估方法,辅助医师为DDH患儿制定诊疗方案.
1 实验部分 1.1 临床资料本实验共收集来自12名儿童的共24例双髋数据.12名儿童年龄均为15岁以内:5名儿童在0~5岁,4名儿童6~10岁,3名儿童11~15岁;12名儿童中男性5例、女性7例.12名儿童中包含DDH患者6例,该6例均为单侧DDH患者,其中4例患儿患髋为左侧,2例患儿患髋为右侧;其余6例为正常对照者.6例患儿中0~5岁3例、6~10岁2例、11~15岁1例.所有儿童均采用GE 3.0 T超导型MRI扫描仪(型号为Discovery 750W)和32通道相控阵体线圈进行髋部MRI扫描,使用脉冲序列为3D-CUBE T1.扫描体位为冠状扫描,扫描范围上至股骨上部髋臼,下至股骨大粗隆,扫描层厚为1.6 mm,显示视野为380 mm,重复时间为400~650 ms,回波时间为10~18 ms,翻转角度为90˚,以便得到使髋关节中股骨、盆骨等结构最清晰显示的可用于形态学参数观测的结构像.患者体位仰卧位,所有患者均无既往髋关节手术史.
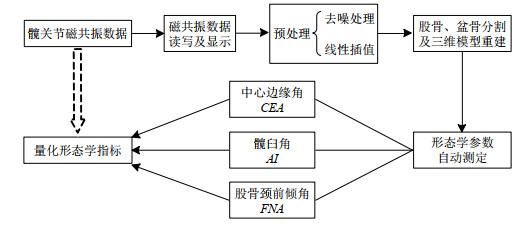
1.2 定量评估方法为实现高精度的形态学参数(CEA、FNA、AI)定量分析,首先在对DDH患儿的磁共振图像进行预处理后,利用图像分割算法对股骨、盆骨进行分割,再对分割后的图像进行三维重建.在重建图像的基础上,根据所需形态学参数的特性设计算法实现其自动测定.针对儿童DDH的磁共振形态学评估方法流程如图 1所示.
|
图 1 本研究中针对DDH患儿的磁共振形态学定量评估方法
Fig. 1 Schematic diagram of quantitative MRI-based morphological evaluation for children with DDH in this research
|
本实验前期采用了3D-FSPGR(fast spoiled gradient recalled)、3D-Fiesta-C(fast imaging employing steady state acquisition with cycled phases)、3D-MERGE(multiple-echo recalled gradient echo)、3D-CUBE T1等序列进行模拟成像实验.经过比较各个序列的成像效果,最终选择对髋关节中股骨、盆骨等区域显示对比度最佳的3D-CUBE T1序列为本实验成像序列.成像结果以医学图像标准格式DICOM(digital imaging and communications in medicine)格式存储.获取实验所需图像数据后,由于原始医学图像中存在噪声和各向异性的问题,因此需要对数据进行预处理,以消除不必要的影响,防止干扰接下来的分割与测量过程.图像的预处理主要包括去噪和各向同性处理,通过编写Matlab脚本程序实现.
(1)去噪处理
用于磁共振图像去噪的方法包括基于小波变换的滤波方法、基于稀疏性的去噪方法、中值滤波和高斯滤波等[20].基于小波变换的滤波可以较好地刻画信号的边缘、断点等特征,但是计算速度慢.基于稀疏性的去噪方法对于图像平滑区的处理效果较好,但是容易损耗图像丰富的纹理信息.中值滤波可以很好地过滤椒盐噪声,但是易导致图像不连续.而磁共振图像中的噪声主要为里斯噪声、高斯噪声和瑞利噪声.当磁共振图像中的信噪比大于2时,里斯分布将转换为高斯噪声分布;而当信噪比接近0时,它将收敛为瑞利分布.临床磁共振图像的信噪比大多数较高,因此主要出现高斯噪声.高斯滤波作为一种线性滤波器,被广泛应用于图像平滑和噪声处理,对高斯噪声的平滑效果最好.因此本实验选择高斯滤波对图像进行去噪处理[21],高斯滤波的模板为:
| $G(x, y) = \frac{1}{{2{\rm{ \mathsf{ π} }}{\sigma ^2}}}\exp ( - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}})$ | (1) |
(1) 式所示近似高斯核生成的二维矩阵模板与原始图像相乘得到平滑后的图像.其中
(2)各向同性处理
医学图像采集时以层方式进行三维扫描,因而所得二维层图像的分辨率和层间距不同,一般情况下层间距是大于分辨率的,即图像在x、y轴方向的分辨率和z轴方向不同.在这种情况下,取得的三维医学图像是各向异性的,而在后续图像处理时要求图像各向同性.本文采集的磁共振数据二维分辨率为0.74 mm,层间距为0.8 mm,因此需要对髋关节磁共振图像在z轴方向进行重取样,使其达到各个方向一致.通常使用插值法调整图像分辨率,本文使用缩放性较好的双线性插值方法对图像数据的分辨率进行调整[22].对目标像素点,设置其浮点坐标为
| $\begin{gathered} p(x' + \mathit{\Delta} x', y' + \mathit{\Delta} y') = (1 - \mathit{\Delta} x')(1 - \mathit{\Delta} y')^*p(x', y') + (1 - \mathit{\Delta} x')\mathit{\Delta} y'^*p(x', y' + 1) \\ {\rm{ }} + \mathit{\Delta} x'(1 - \mathit{\Delta} y')^*p(x' + 1, y') + \mathit{\Delta} x'\mathit{\Delta} y'^*p(x' + 1, y' + 1) \\ \end{gathered} $ | (2) |
其中,
本研究使用开源图像处理软件3D Slicer选定感兴趣区域(region of interest,ROI),包括盆骨及股骨的区域.经临床骨科及放射科医师指导,结合软件内置level-set工具、Graph-cut分割算法完成对磁共振数据的半自动分割.与其他类似软件相比,3D Slicer软件是完全开源的,可以轻松扩展和重新编译.并且可以通过开发插件的形式开发新功能,因此未来可将后文提及的自动测量算法以插件的形式集成到3D Slicer中.
随着MRI技术的日趋发展,MRI扫描时间大大缩短,但这也使得数据量较大的三维磁共振图像的重建更加复杂.三维磁共振图像重建时,复杂的算法极易耗尽计算机内存,并且多个片层图像的重建受计算机硬件影响较大[23].本文结合3D Slicer软件,只需在软件三维渲染功能基础上,改善三维模型边缘平滑度,调整各项参数即可得到分割后股骨及盆骨的三维立体模型,缺点在于分割过程并不完全自动.未来可开发针对髋关节的分割算法,提高分割过程的自动化程度.图 2所示为由1例正常对照者髋关节磁共振图像分割重建后所得的髋关节三维模型,绿色为股骨部分,黄色为盆骨部分.图中字母标识为五个方向,分别为右(right,R)、上(superior,S)、左(left,L)、下(interior,I)和后(posterior,P).导出三维模型,以立体光刻(stereo lithography,STL)格式储存.

|
图 2 包含股骨及盆骨的髋关节三维模型.R(右),L(左),S(上),I(下),P(后) Fig. 2 3D model of hip joint including femur and pelvis. R (right), L (left), S (superior), I (interior), P (posterior) |
基于髋关节三维分割结果,我们设计了算法,并编写Matlab脚本程序实现髋关节三项形态学参数,包括CEA、AI和FNA的自动测定.
(1)CEA自动测量的算法设计
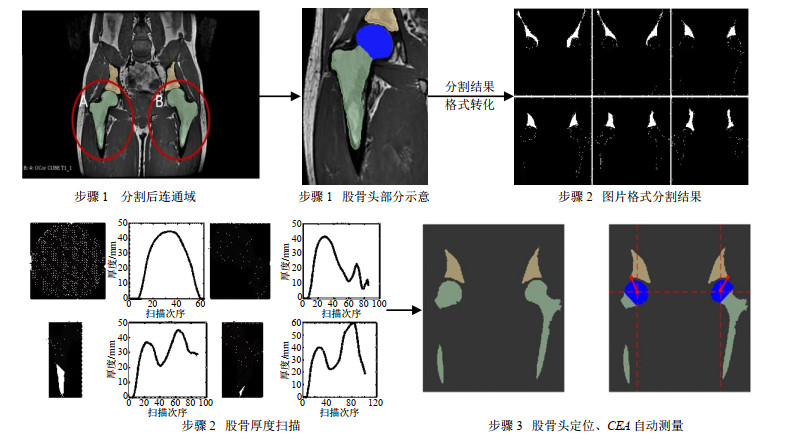
CEA定义为垂直于穿过股骨头中心的基线绘制的线和连接股骨头中心与髋臼上边界的线所形成的角度.如图 3所示,虚线为垂直于两侧股骨头中心点连线,实线为连接股骨头中心与髋臼最外缘的连线,虚线与实线之间的夹角即为CEA.基于上述分割结果,提取股骨部分的股骨头区域.转化分割结果为图片格式,绘制股骨厚度分布图,以此定位股骨头及其中心点,具体实现步骤如下所述,并如图 4所示.

|
图 3 中心边缘角示意图(左)及中心边缘角手动测定(右) Fig. 3 Schematic diagram (left) and manual measurement (right) of CEA |
|
图 4 本文设计的中心边缘角自动测量方法 Fig. 4 The proposed method for CEA automatic measurement |
步骤1:按照冠状面磁共振数据,在每一帧分割得到连通区域A和B部分,定位黄色盆骨区域的最外缘,对股骨区域定位股骨头类圆形部分(图 4蓝色部分)质心.
步骤2:基于分割所得三维重建模型,导出分割结果,转化为单帧图像格式.对股骨头部分实现左右两侧股骨的平面厚度扫描(对左侧股骨行自右上至左下的扫描,对右侧股骨行自左上至右下的扫描)并生成左右两侧股骨厚度分部图,找到厚度图中最大厚度所对应区域,即为股骨头中心点所在层面,厚度值两次为0(或第一次到达波谷处)之间所包含的区域即为股骨头所在平面.
步骤3:确定股骨头部分及股骨头中心点所在位置,寻找连接股骨头中心点与盆骨连通域内的斜率最小正值点和负值点,即可确定两侧髋臼最外缘.连接两侧股骨头中心点并分别过两侧股骨头中心点作股骨头中心点连线的垂线,分别连接两侧股骨头中心点与髋臼最外缘点.计算两侧股骨头中心点与两侧髋臼最外缘点的连线与垂线之间所成角度.
经过以上步骤,每帧磁共振图像都可得到左右髋各一角度.根据CEA定义,股骨头中心点所在帧的角度为待测的CEA.多帧图像中股骨厚度最大点所对应的帧为股骨头中心点所在帧,该帧角度即为本例数据的CEA.
(2)AI自动测量的算法设计
AI定义为髋关节两侧髂骨最低点(泪点)之间的连线与泪点和髋臼最外缘之间连线的夹角,如图 5所示.AI的自动测定算法设计与CEA类似.根据AI定义,可知AI的自动测量需要实现泪点与髋臼最外缘点的定位.CEA的自动测量中股骨头中心点的位置可以辅助泪点与髋臼最外缘点的定位,如CEA自动测量的算法设计中步骤2所述.因此结合CEA算法流程可得到AI的自动测量方法.具体实现步骤如下所述,并如图 6所示.

|
图 5 髋臼角示意图(左)及髋臼角的手动测定(右)
Fig. 5 Schematic diagram (left) and manual measurement (right) of AI
|

|
图 6 本文设计的髋臼角自动测量方法 Fig. 6 The proposed method for AI automatic measurement |
步骤1:按照厚度搜索的方法,绘制髋关节磁共振图像股骨部分逐帧厚度分布图,确定股骨头区域及股骨头中心点所在位置.
步骤2:基于股骨头中心点的位置遍历盆骨区域,确定使股骨头中心点与盆骨区域某点连线的最大及最小角度,以此确定泪点及髋臼最外缘位置.
步骤3:自动连接髋关节两侧泪点,再分别连接两侧泪点与髋臼最外缘,计算两线之间所夹锐角.
经过以上步骤,每帧磁共振图像都可得到左右髋各一角度.根据AI角定义,泪点所在帧为待测的AI角.而步骤2基于股骨头中心点遍历盆骨区域所得角度中,最小角度对应层面即为泪点所在帧,因此该帧角度结果为本例数据的AI.
(3)FNA自动测量的算法设计
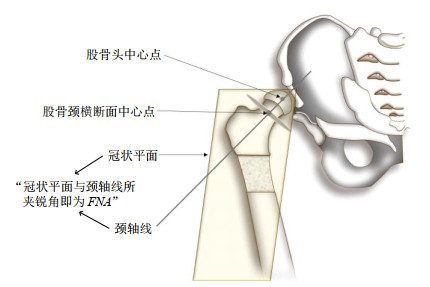
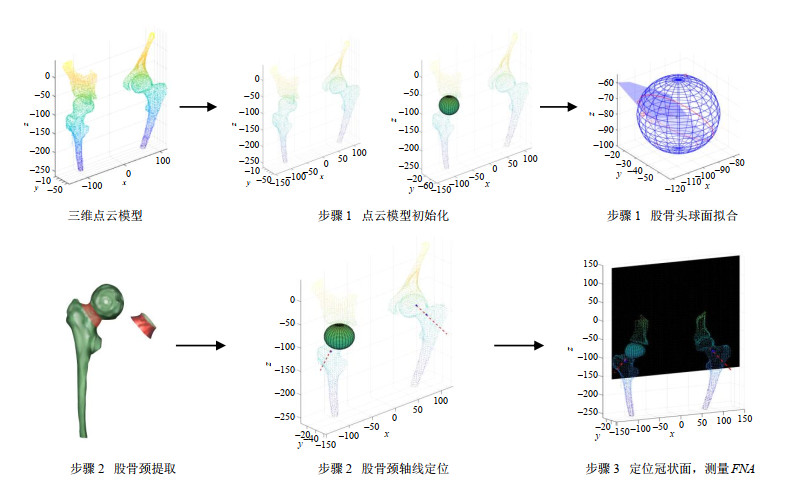
如图 7所示,有一贯穿股骨轴的冠状平面,连接股骨头中心点与股骨颈横断面的中点的直线即股骨颈轴线,冠状平面与股骨颈轴线之间的夹角即为FNA.实现FNA的自动测量需实现股骨头中心点与股骨颈轴线的自动定位.为方便对三维模型的形态学测量,我们对上述分割重建后的.STL格式的三维模型降采样得到三维点云模型,点云中每点对应唯一的三维坐标.具体实现步骤如下所述,并如图 8所示.
|
图 7 股骨颈前倾角示例 Fig. 7 Schematic diagram of FNA |
|
图 8 本文设计的股骨颈前倾角自动测量方法 Fig. 8 The proposed method for FNA automatic measurement |
步骤1:股骨头中心的确定.使用三维霍夫变换初始化磁共振图像,检测股骨头类球部分,然后采用迭代最小二乘算法拟合股骨头球心坐标.适用于球体表面中每个点的霍夫变换极坐标映射方程如(3)式所示,r为球体半径,
| $\begin{gathered} {c_x} = x - r\cos \theta \sin \varphi \\ {c_y} = y - r\sin \theta \sin \varphi \\ {c_z} = z - r\cos \varphi \\ \end{gathered} $ | (3) |
接下来,利用最小二乘算法拟合股骨头球面,三维空间中球面方程如(4)式所示:
| ${x^2} + {y^2} + {z^2} - 2{x_0}x - 2{y_0}y - 2{z_0}z + x_0^2 + y_0^2 + z_0^2 = {R^2}$ | (4) |
其中
| $cx + dy + ez + f = {x^2} + {y^2} + {z^2}$ | (5) |
然后得到最小二乘法的误差方程表达式:
| $V = AX - L$ | (6) |
其中
步骤2:股骨颈轴线的确定.股骨颈轴线是与股骨颈的三维点云最匹配的单叶双曲面模型的中心轴,即股骨头中心点与股骨颈切面的中心点之间的连线.基于最小二乘法可以估计该双曲面模型的各项几何参数.单叶双曲面方程具有(7)式所示的表达形式:
| ${(\frac{x}{a})^2} + {(\frac{y}{b})^2} - {(\frac{z}{h})^2} = 1$ | (7) |
其中a、b决定股骨颈的椭圆度,h决定增长率,该双曲面的平均形状参数为:
步骤3:股骨颈轴线与点云冠状面之间的夹角即为待测角FNA.
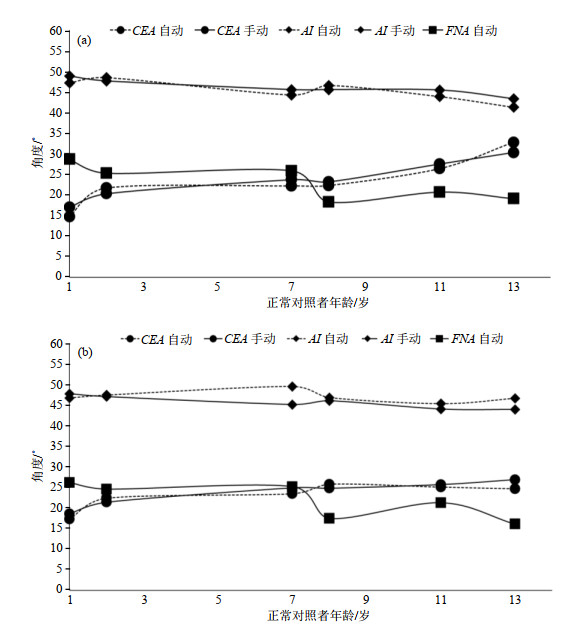
2 结果与讨论图 9为正常儿童左髋和右髋的髋关节形态学参数测量结果,横坐标为年龄.CEA、AI的手动测量结果经两名从业5~10年的放射科及骨科医师确认,数据上传影像归档和通信系统(picture archiving and communication systems,PACS),测量平台为GE AW VolumeShare5后处理工作站.图 9中没有FNA手动测量结果,这是由于FNA的临床测量一般需要结合股骨髁部位辅助定位冠状面,再进行手动计算.而本文实验数据扫描范围下至股骨大粗隆,并不包含股骨髁部分,所以无法获得FNA的手动测量结果.正常对照者中0~5岁2例,6~10岁2例,11~15岁2例.从图 9可以发现正常儿童的CEA随着年龄呈上升趋势,而AI、FNA呈下降趋势.健康儿童的左髋CEA测量范围为17.0˚~30.3˚,AI为43.4˚~48.9˚,FNA为19.1˚~28.7˚.右髋CEA测量范围为18.7˚~27.0˚,AI为44.1˚~47.9˚,FNA为16.2˚~26.3˚.对健康儿童左右髋的CEA、AI、FNA测量结果分别进行成对t检验,p值分别为:
|
图 9 正常对照者的(a)左髋和(b)右髋的CEA、AI的自动及手动测量结果、FNA的自动测量结果 Fig. 9 Results of CEA, AI automatic and manual measurements, and FNA automatic measurement for (a) left and (b) right hips of the normal children |
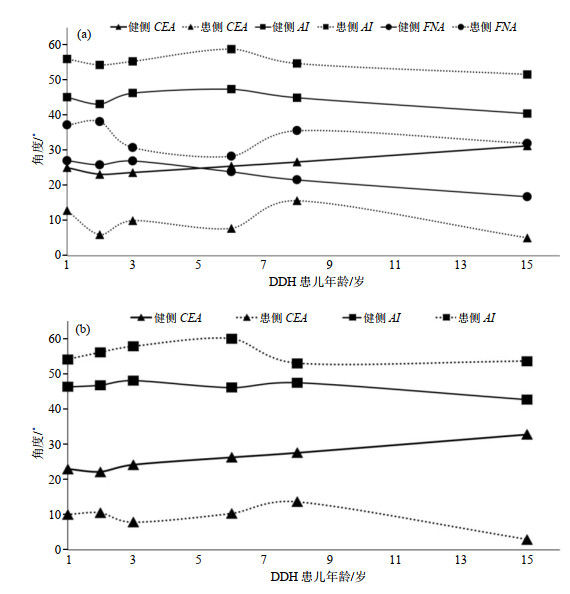
图 10(a)为6例单侧DDH患儿健侧髋与患侧髋的CEA、AI、FNA自动测量结果,横坐标为年龄,其中0~5岁3例,6~10岁2例,11~15岁1例.可以发现单侧DDH患儿的健侧髋CEA、AI、FNA的自动测量结果与图 9一致.而患侧髋的CEA较健侧髋显著减小,基本在15˚以下;患侧髋AI较健侧髋明显增大,基本在50˚以上;患侧髋FNA较健侧髋显著增大,基本在30˚以上.且对比图 10(b),DDH患儿CEA、AI角度自动测量结果与手动测量基本吻合.
|
图 10 (a) DDH患儿患侧髋和健侧髋的CEA、AI、FNA自动测量结果;(b) DDH患儿患侧髋和健侧髋的CEA、AI手动测量结果 Fig. 10 (a) Results of CEA, AI and FNA automatic measurements of children with DDH; (b) Results of CEA and AI manual measurements of children with DDH |
文献表明,4岁儿童的CEA正常范围为(21.62˚±6.23˚);10~14岁时快速增长,发生从(24.54˚±5.47˚)到(31.11˚±6.20˚)的变化,CEA小于正常范围提示DDH可能[25].AI在10岁的时候平均值是46.72˚,10岁以后会有所下降,18岁时保持在约39.10˚,18岁以后在38˚~39˚波动,AI大于正常范围提示DDH可能[26].FNA在6岁时平均为26.60˚,10岁时平均为20.89˚,呈现随年龄增长而逐渐减小的趋势,成年后一般在12˚~15˚,FNA大于正常范围的儿童可能伴有DDH[27].
本文DDH患儿患侧髋的自动测量结果符合上述DDH所致角度异常变化,而且其健侧髋及健康儿童双侧髋的测量结果均属于临床正常范围.由此可知,本文方法能有效测量DDH相关的CEA、AI、FNA三个参数,且对DDH患儿角度变化较为敏感.
使用SPSS软件对全部24例儿童双侧髋的CEA、AI的自动测量与手动测量结果分别计算相关系数,发现手动测量与自动测量的CEA、AI具有统计学强相关性(CEA相关系数r1=0.97,AI相关系数r2=0.91).自动测量数据与手动测量数据的方差分析如表 1所示.
| 表 1 24例儿童双侧髋的CEA、AI的自动测量与手动测量结果的方差分析 Table 1 Variance analysis between automatic measurements and manual measurements for CEA and AI |
CEA方差分析中,p=0.891,大于0.05;且F=0.019,小于F crit=4.052,说明在置信区间内,CEA自动测量与手动测量结果没有显著差异.AI方差分析中,p=0.861,大于0.05;且F=0.031,小于F crit=4.052,说明在置信区间内,AI自动测量与手动测量结果同样无显著差异.这进一步说明本文方法能够有效地测量CEA与AI.
根据DDH的Tonnis分型[28],DDH脱位程度分为Ⅰ˚、Ⅱ˚、Ⅲ˚和Ⅳ˚,其中Ⅰ、Ⅱ度为半脱位,Ⅲ、Ⅳ˚为全脱位.因此在有效测量髋关节形态学参数的基础上,若扩大数据量,本文方法未来可建立基于形态学量化指标的DDH分级标准.
3 结论本文提出了一种DDH儿童的磁共振形态学定量评估方法,该方法运用图像处理技术,结合开源软件3D Slicer完成髋关节的分割和三维重建.在此基础上设计定量算法,最终实现CEA、AI、FNA三项髋关节形态参数的测定.实验表明,本文方法可以有效地实现髋关节形态参数的自动测定,在置信区间内,CEA和AI的手动测量结果与自动测量结果没有显著差异.且健康儿童和DDH患儿健侧髋CEA、AI、FNA自动测量结果均在临床正常范围.在后续实验中可收集扫描范围至股骨髁的磁共振数据,完善FNA的自动测量与手动测量的对比.本文所述针对儿童DDH的形态学定量评估方法可以帮助医生对DDH更直接地做出诊断,更好地制定治疗方案.
本文主要从DDH所致形态学改变来制订DDH的定量评估方法,临床发现,在DDH更早期,软骨中蛋白多糖和含水量分布等生化成分有显著变化[29].MRI的弛豫时间等参数与成像组织的蛋白结构等密切相关[30],T2 mapping、T1rho等序列常用于软骨的生化成分定量[31].因此后期可制订DDH磁共振生化参数的定量评估方法,结合本文所提及的形态学参数定量评估方法,更好地利用MRI的优势,形成全面的儿童DDH的磁共振定量评估.
| [1] | ROOF A C, JINGUJI T M, WHITE K K. Musculoskeletal screening:developmental dysplasia of the hip[J]. Pediatr Ann, 2013, 42(11): 229-235. |
| [2] | ÖZTÜRK H, ÖZTEMÜR Z, BULUT O, et al. Arthroscopic-assisted surgical treatment for developmental dislocation of the hip before the age of 18 months[J]. Arch Orthop Traum Su, 2013, 133(9): 1289-1294. DOI: 10.1007/s00402-013-1781-y. |
| [3] | TÖZÜN İ R, AKGÜL T, ŞENSOY V, et al. The results of monoblock stem with step-cut femoral shortening osteotomy for developmentally dislocated hips[J]. Hip Int, 2016, 26(3): 270-277. DOI: 10.5301/hipint.5000338. |
| [4] |
WANG L, SHENG M, ZHANG M, et al. Correlation study of MRI and pathology findings of children with developmental dislocation of the hip[J].
Radiologic Practice, 2015, 30(3): 282-285.
王亮, 盛茂, 张闽, 等. 儿童发育性髋关节脱位MRI表现与病理对照研究[J]. 放射学实践, 2015, 30(3): 282-285. |
| [5] | STARR V, HA B Y. Imaging update on developmental dysplasia of the hip with the role of MRI[J]. Am J Roentgenol, 2014, 203(6): 1324-1335. DOI: 10.2214/AJR.13.12449. |
| [6] | AUDENAERT E A, BAELDE N, HUYSSE W, et al. Development of a three-dimensional detection method of cam deformities in femoroacetabular impingement[J]. Skeletal Radiol, 2011, 40(7): 921-927. DOI: 10.1007/s00256-010-1021-2. |
| [7] | HAREENDRANATHAN A R, ZONOOBI D, MABEE M, et al. Hip segmentation from MRI volumes in infants for DDH diagnosis and treatment planning[C]//201638th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2016: 1046-1049. |
| [8] |
TU Y J. MRI measurement of cartilaginous acetabular anteversion in DDH and normal children[J].
Orthopedic Journal of China, 2014, 22(17): 1557-1562.
涂以济. 发育性髋关节脱位儿童与正常儿童软骨性髋臼前倾角的MRI研究[J]. 中国矫形外科杂志, 2014, 22(17): 1557-1562. |
| [9] |
WANG L, SHENG M, GUO W L, et al. MRI study of the infantile developmental dislocation of the hip[J].
Journal of Practical Radiology, 2014, 30(4): 649-652.
王亮, 盛茂, 郭万亮, 等. 婴幼儿发育性髋关节脱位MRI评价[J]. 实用放射学杂志, 2014, 30(4): 649-652. |
| [10] | BELTRAN L S, ROSENBERG Z S, MAYO J D, et al. Imaging evaluation of developmental hip dysplasia in the young adult[J]. AJR Am J Roentgenol, 2013, 200(5): 1077-1088. DOI: 10.2214/AJR.12.9360. |
| [11] | DOUIRA-KHOMSI W, SMIDA M, LOUATI H, et al. Magnetic resonance evaluation of acetabular residual dysplasia in developmental dysplasia of the hip:a preliminary study of 27 patients[J]. J Pediatr Orthop, 2010, 30(1): 37-43. |
| [12] | XIA Y, FRIPP J, CHANDRA S S, et al. Automated 3D quantitative assessment and measurement of alpha angles from the femoral head-neck junction using MR imaging[J]. Phys Med Biol, 2015, 60(19): 7601-7616. |
| [13] | AL-BASHIR A K, AL-ABED M, SHARKH F M A, et al. Algorithm for automatic angles measurement and screening for developmental dysplasia of the hip (DDH)[C]//201537th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2015. |
| [14] | LI B, LU H B, CAI W L, et al. Computer aided diagnosis and treatment planning for developmental dysplasia of the hip[J]. Proceedings of the SPIE, 2005, 5744: 781-788. DOI: 10.1117/12.595645. |
| [15] |
LIU Z X, LIU W D, WANG J F, et al. The study of acetabular index in children with developmental dislocation of the hip using MRI[J].
Radiologic Practice, 2004, 19(1): 1-2.
刘志新, 刘卫东, 王继芳, 等. 幼儿发育性髋关节脱位髋臼指数的MRI研究[J]. 放射学实践, 2004, 19(1): 1-2. |
| [16] | BERNARD M. Normal values of the hip joint for the evaluation of X-rays in children and adults[J]. Joint Replacement Arthroplasty, 2007, 73(7): 815-817. |
| [17] | BURKE N G, DEVITT B M, BAKER J F, et al. Outcome of periacetabular osteotomy for the management of acetabular dysplasia:experience in an academic centre[J]. Acta Orthop Belg, 2011, 77(1): 33-40. |
| [18] | SPENCE G, HOCKING R, WEDGE J H, et al. Effect of innominate and femoral varus derotation osteotomy on acetabular development in developmental dysplasia of the hip[J]. JBJS, 2009, 91(11): 2622-2636. DOI: 10.2106/JBJS.H.01392. |
| [19] | SUGANO N, NOBLE P C, KAMARIC E, et al. The morphology of the femur in developmental dysplasia of the hip[J]. J Bone Joint Surg BR, 1998, 80(4): 711-719. DOI: 10.1302/0301-620X.80B4.0800711. |
| [20] |
ZHANG B, XIE H B, YAN X, et al. Rotation invariant non-local means for noise reduction in magnetic resonance images[J].
Chinese J Magn Reson, 2018, 35(2): 162-169.
张波, 谢海滨, 严序, 等. 旋转不变的非局域均值算法在磁共振图像去噪中的应用[J]. 波谱学杂志, 2018, 35(2): 162-169. |
| [21] | YU Z, BAJAJ C. A fast and adaptive method for image contrast enhancement[C]//2004 International Conference on Image Processing, 2004, 2004, 2: 1001-1004. |
| [22] |
FENG H J, TAO S J, LI L. Doublelinear inserting algorithm based image zooming and its realization with VC++[J].
Computer Applications and Software, 2004, 21(7): 117-119.
冯慧君, 陶素娟, 李隆. 基于双线性插值算法的图像放缩技术与实现[J]. 计算机应用与软件, 2004, 21(7): 117-119. |
| [23] |
XU J W, XU J, ZHOU X D, et al. Multi-GPU distributed magnetic resonance image reconstruction based on gadgetron[J].
Chinese J Magn Reson, 2018, 35(3): 303-317.
徐嘉文, 徐健, 周晓东, 等. 基于Gadgetron平台的多GPU分布式磁共振图像重建[J]. 波谱学杂志, 2018, 35(3): 303-317. |
| [24] | MASJEDI M, HARRIS S J, DAVDA K, et al. Mathematical representation of the normal proximal human femur:application in planning of cam hip surgery[J]. Proc Inst Mech Eng H, 2013, 227(4): 421-427. |
| [25] |
SHI Y Y, LIU T J, ZHAO Q, et al. The measurement of center-edge angle of hips in a healthy Chinese population[J].
Chinese Journal of Pediatric Surgery, 2010, 2: 118-122.
石永言, 刘天婧, 赵群, 等. 中国人髋关节中心边缘角正常值的测量[J]. 中华小儿外科杂志, 2010, 2: 118-122. |
| [26] |
SHI Y Y, LIU T J, ZHAO Q, et al. The measurements of normal acetabular index and Sharp acetabular angle in Chinese hips[J].
Chinese Journal of Orthopedics, 2010, 8: 748-753.
石永言, 刘天婧, 赵群, 等. 中国人髋关节髋臼指数和Sharp角正常值的测量[J]. 中华骨科杂志, 2010, 8: 748-753. |
| [27] | GULAN G, MATOVINOVIĆ D, NEMEC B, et al. Femoral neck anteversion:values, development, measurement, common problems[J]. Coll Antropol, 2000, 24(2): 521-527. |
| [28] | COLEMAN S S. Congenital dysplasia and dislocation of the hip[M]. St. Louis: Mosby, 1978. |
| [29] | NING B, WANG P, PEI X H, et al. Early cartilage degeneration in a rat experimental model of developmental dysplasia of the hip[J]. Connect Tissue Res, 2012, 53(6): 513-520. DOI: 10.3109/03008207.2012.700346. |
| [30] |
WEN Y, LIN D H. Protein dynamics studied by NMR spin relaxation[J].
Chinese J Magn Reson, 2012, 29(2): 288-306.
文祎, 林东海. 基于NMR自旋弛豫技术的蛋白质动力学研究[J]. 波谱学杂志, 2012, 29(2): 288-306. |
| [31] | GOLD S L, BURGE A J, POTTER H G. MRI of hip cartilage:joint morphology, structure, and composition[J]. Clin Orthop Relat Res, 2012, 470(12): 3321-3331. DOI: 10.1007/s11999-012-2403-7. |
 2020, Vol. 37
2020, Vol. 37 
