2. 中国科学院大学, 北京 100049;
3. 医学人工智能研究中心(中国科学院 深圳先进技术研究院), 广东 深圳 518055
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Research Center for Medical AI, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China
目前,已有很多加快数据采集速度的方法用于磁共振成像(Magnetic Resonance Imaging,MRI),以解决其采集速度较慢的问题[1].比如,早期基于笛卡尔空间的部分傅里叶重建[2]方法,只需采集约1/2的k空间数据,然后利用k空间本身的复数共轭对称特性,即可填充未采集的k空间,进而得到重建图像;随后的并行成像方法[3, 4]通过在相位编码方进行降采样减少了扫描时间.然而,在实际扫描中,k空间数据并非完全共轭对称,因此,重建图像会产生伪影,且部分傅里叶重建方法的加速倍数较低(小于等于2倍加速),无法满足快速扫描的需求.后来,有研究利用多通道线圈含有的冗余信息进一步加速成像,在k空间恢复出未采样的相位编码线,并消除降采样的混叠伪影,例如GRAPPA(GeneRalized Autocalibrating Partially Parallel Acquisitions)[4]等基于k空间的并行重建方法;或是在图像空间对混叠的像素点进行分离,例如SENSE(SENSitivity Encoding)[3]等基于图像空间的并行重建方法.由于基于k空间和图像空间的并行重建方法降采样相位编码线,并利用多通道线圈所含有的冗余信息进行图像重建,从而相对于全采样有
深度学习方法近年被广泛应用于MRI领域,主要可以分为两类[9, 10]:一类是将传统算法进行网络化学习,另一类是利用神经网络进行端到端的学习[11].第一类方法一般基于图像域和k空间的重建.通常,基于深度学习的重建方法都需要极大的训练数据量,因此有研究提出利用扩展训练样本来提升重建性能[12],但最近提出的基于三层人工神经网络进行重建的k空间差值鲁棒人工神经网络(Robust Artificial-neural-networks for k-space Interpolation,RAKI)方法[13]通过在k空间进行实时插值,避免了深度学习的大数据量学习过程.传统的基于k空间的GRAPPA并行成像方法[4]是从自动校准信号(Auto-Calibration Signal,ACS)数据中,利用欠采样部分和全采样部分,估计出一个线性权重,然后将这个线性权重应用到降采样数据中,从而填充未采集的相位编码线,最后经过逆傅里叶变换和线圈融合技术,获得重建图像.RAKI方法[13]与之类似,区别在于RAKI方法利用一个三层的卷积神经网络(Convolutional Neural Network,CNN)来估计许多个非线性的权重.不同于大多数的深度学习的重建方法,RAKI方法是基于特定扫描数据的方法,不需要其他多余数据来做训练集合.其与最近提出的KIKI-Net方法[14]非常类似,RAKI方法利用了所有射频线圈采集的k空间数据,而并没有对输入网络的数据做数据融合.
目前,对于基于CAIPIRINHA采集[7]的SMS图像重建方法,有传统的基于k空间的SENSE/GRAPPA[15]、Slice-GRAPPA(SG)[5]重建方法.也有基于RAKI的k空间插值方法,其良好的性能已经在传统的并行成像中用不同加速倍数下进行了量化检验[13],还可被应用于SMS图像重建之中[16].此外,虚拟线圈概念(Virtual Coil Concept,VCC)利用了MRI信号在k空间的复数共轭对称性质,利用实际采集的复数信号生成虚拟信号,增加了额外的相位信息,从而实现更高倍速的加速.VCC已被用于GRAPPA重建,实现了4~7倍的成像加速[17].
本文提出了一种基于VCC和RAKI的SMS图像重建方法,并将其命名为VIRGINIA(VIRtual conjuGate coIls Neural-networks InterpolAtion).VIRGINIA方法首先将实际采集的ACS数据和通过VCC方法生成的虚拟共轭数据结合成为一个训练样本集合,然后利用该训练样本分别构建RAKI网络的输入和输出.在RAKI网络的训练过程中,我们使用ADAM优化器[18]以0.001的学习率在TensorFlow的框架下搭建模型进行1 500轮的训练.在重建过程中,实际采集的SMS混叠数据作为网络的输入,并将网络的输出数据和输入的SMS数据进行融合后则得到完整的多个单片层多通道k空间数据.在将k空间数据进行傅里叶逆变换后,经过平方和(Sum of Square,SoS)进行多通道数据融合,得到最终的重建图像.本文将SG、RAKI和VIRGINIA在2、3、4、5和15倍加速下的重建结果进行了对比,并且利用结构相似指数(Structural SIMilarity index,SSIM)、峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和均方根误差(Root Mean Square Error,RMSE)对使用不同方法获得的重建图像质量进行了客观分析和评价.
1 理论基础 1.1 SMS原理SMS利用MB复合射频脉冲对多个片层同时激发,并利用多通道线圈的空间敏感性来解开接收到的SMS混叠信号,分离各层图像.SMS技术可以在一个层的采集时间里同时获得被激发的多个层图像,从而有效地缩短采集时间.由于在不同层的同一位置的像素之间的线圈敏感度差异性对解开混叠的影响非常较大,因此,CAIPIRINHA方法对同时激发的每一层引入了FOV偏移[7](图 1).该方法使得不同层图像之间的同一对应像素位置处的线圈敏感度差异性变大,非常有利于重建性能提升.层间FOV偏移的SMS数据采集方法如(1)式所示:
| $\rho (y) = \sum\limits_{m = - N{\rm{/2}}}^{N{\rm{/2}} - {\rm{1}}} {\left[ {\sum\limits_{z = 1}^{MB} {{S_z}(m\mathit{\Delta} k){{\rm{e}}^{{\mathit{\Phi} _z}(m)}}} } \right] \times {{\rm{e}}^{{\rm{i}}m \cdot \mathit{\Delta} k \cdot y}}} = \sum\limits_{z = 1}^{MB} {{\rho _z}(y - \mathit{\Delta} {y_z})} $ | (1) |
|
图 1 以3倍层加速为例,层间相位偏移为2π/3,对应FOV/3偏移 Fig. 1 Example of 3× slice acceleration, the inter-slices phase shift is 2π/3, corresponding to FOV/3 shift |
其中,N表示空间编码点数;m是k空间编码位置索引,取值范围为
在具体实现的时候,选择合适的
SG方法是用来从SMS采集的多层同时混叠数据中恢复多层数据的一种经典的线性重建方法[5].对于SG算法,k空间信号的拟合方程如下:
| ${S_{j, z}}({k_x}, {k_y}) = \sum\limits_{l = 1}^L {\sum\limits_{{b_x} = - {B_x}}^{{B_x}} {\sum\limits_{{b_y} = - {B_y}}^{{B_y}} {w_{j, z, l}^{{b_x}, {b_y}}{S_{l, collapse}}({k_x} - {b_x}\mathit{\Delta} {k_x}, {k_y} - {b_y}\mathit{\Delta} {k_y})} } } $ | (2) |
其中,L是磁共振采集的实际线圈数目,
| ${w_{opt}} = \arg \mathop {\min }\limits_w \left\| {\left. {b - Aw} \right\|} \right.$ | (3) |
以核大小
RAKI方法本质上是一种针对SG方法的非线性改进,它虽然基于人工神经网络进行重建,但是又区别于传统的深度学习方法,具有如下特点[13]:(1)非大数据集的深度学习方法.由于RAKI中无论是训练数据还是测试数据都不依赖于其他扫描对象的扫描数据,因此只需要基于本次扫描对象的ACS数据构建训练数据,实际采集的降采样数据作测试数据,即可根据该方法得到最终的重建图像. (2)多线圈通道输入.RAKI直接使用了采集的多通道数据作为训练和测试的网络输入数据.(3)k空间直接重建.RAKI网络的输入输出都是基于k空间进行的.(4)兼容传统的数据采集协议.基于RAKI的前三项特点,采集获得的k空间数据直接可以用RAKI网络进行重建.RAKI原理可用(4)式表示:
| ${S_{j, z}}({k_x}, {k_y} - m\mathit{\Delta} {k_y}) \approx {f_{j, m}}\{ {[{S_{l, collapse}}({k_x} - {b_x}\mathit{\Delta} {k_x}, {k_y} - {b_y}\mathit{\Delta} {k_y})]_{{b_x} \in [ - {B_x}, {B_x}], {b_y} \in [ - {B_y}, {B_y}], l \in [1, L]}}\} $ | (4) |
其中,m为k空间位置编码索引,非线性拟合体现在函数f上,它代替(2)式中线性核w,代之以三层CNN中的共享权和ReLu函数[16],通过非线性函数隐式表达来联系输入输出数据之间的映射关系.CNN应用需要在实数域进行,复数信号的虚数部分可以直接扩展到线圈方向.经过数次实验比较,本文使用两层CNN而非三层CNN,减少了参数量和训练时间,但和三层CNN相比,重建图像质量并没有明显变化.
1.4 VIRGINIA重建原理本文提出的用于SMS图像重建的VIRGINIA方法首先生成VCC信号.如(5)式所示,它表示线圈j的k空间信号
| $S_j^{vcc}(k) = S_j^*( - k)\ \ \ \ \ \ \ \ \ \ j = 1, \cdots , L$ | (5) |
其中,*表示转置操作,L是相控阵列的部件数,即线圈个数.
两层CNN网络实现的简要表达式如(6)式所示:
| $F(s) = {F_2}({F_1}(s)) = {w_2} * (ReLu({w_1} * s))$ | (6) |
其中,网络信号

|
图 2 VIRGINIA网络的训练数据构建图,以MB=3为例.对于采集到的3层k空间的ACS数据(图中左上蓝色方框所示),利用VCC方法生成和原数据同样大小的虚拟ACS数据(左下黑色方框所示),然后,对采集的ACS数据和虚拟ACS数据,分别按图中所示,进行逆傅里叶变换(IDFT)后,在读出方向(即频率编码方向)上连接各层图像(如图右上方和右下方所示),最后傅里叶变换回到k空间,获得所有片层连接的k空间数据(橙色方框所示).一组训练数据中一共包含了两份数据,即真实ACS数据和虚拟ACS数据.橙色方框中的数据在读出方向上的所有红色线数据用于训练输入,橙色和蓝色线数据用于训练输出 Fig. 2 Training data construction chart for VIRGINIA, taking acceleration factor MB=3 as an example. Firstly, the virtual ACS data (as indicated by the black box at the bottom left) is generated using VCC method from the acquired ACS data (as indicated by the blue box at the upper left), and after inverse Fourier transformation for all the ACS data as figure, the three images of all coils are concatenated along the readout direction (as shown in the upper right and lower right of the figure), which follows Fourier transformation and acquires all the k-space data of all slices and all coils (as indicated by the orange box). The training data includes two samples, one acquired ACS data and one virtual ACS data. All red lines of the data in the orange box are used for training input, and the remain orange and blue lines of the data are used for training output |

|
图 3 (a) VIRGINIA算法流程图,左边的黄色流程框为训练过程,右边的绿色流程框为重建过程,其中,训练数据生成涉及的预处理P与其逆过程详见图 2,网络框架见图(b);(b)基于二层CNN结构的VIRGINIA重建原理图,该示意图以3倍层加速为例(MB=3),第一层输入的是层方向降采样的k空间数据,数据大小为[Ns, Npe, Nfe, 2Nc]:对于RAKI,Ns为1;对于VIRGINIA,Ns为2.由于CNN不能处理复数数据,因此将虚数部分扩展到线圈方向.该层的卷积滤波器的权重参数为w1,大小为[b1y, b1x, 2Nc, N1],其后接着一个非线性的整流线性单元操作,即ReLu函数,从而实现了采集数据经过第一层网络后的非线性输出.第二层网络通过卷积滤波器w2(大小为[b2y, b2x, N1, Nout],其中Nout=2Nc×(MB-1)),得到k空间数据的缺失部分,经过与输入数据在读出方向的数据融合,获得了大小为[Npe, Nfe×MB, 2Nc]的完整SMS的k空间重建数据
Fig. 3 (a) VIRGINIA algorithm flow chart. The yellow flow box on the left is the training process and the green flow box on the right is the reconstruction process. The preprocessing P involved in the generation of training data and its inverse process are shown in Fig. 2, and the specific network framework is shown in Fig. (b); (b) The two-layer CNN network frame for VIRGINIA reconstruction with MB=3. The downsampling k-space data of the first layer along the slice direction are fed into the network, with the size of [Ns, Npe, Nfe, 2Nc] where Ns=1 for RAKI and Ns=2 for VIRGINIA. Because the CNN cannot deal with the complex, the virtual part is concatenated with the real part along the coil direction. The first-layer filter w1 (its size is [b1y, b1x, 2Nc, N1]) convolves with the downsampling k-space data, followed by a ReLu activation function which produces the nonlinear output. After convolved with the second-layer filter w2 (its size is [b2y, b2x, N1, Nout] and Nout=2Nc×(MB-1)), the missing part in entire k-space (the orange and blue data in the second-row box) is acquired. In the final procedure, through the red lines of input are combined with orange lines and blue lines along the readout direction, the entire k-space data of SMS for all coils are acquired. Through Fourier transform and square of sum, the final reconstructed images can be obtained
|
VIRGINIA算法的实现流程如图 3(a)所示,其涉及的数据构建过程与网络实现部分如图 2和图 3(b)所示.假设模型需要构造的网络输入、输出数据的大小分别为[Ns, Npe, Nfe, 2Nc]、[Ns, Npe, Nfe, 2Nc×(MB-1)](Ns、Npe、Nfe、Nc、MB分别表示为样本个数、相位编码长度、读出长度、线圈个数、同时采集的层数.训练过程中,使用VIRGINIA方法时的Ns为2,使用RAKI方法时的Ns为1).具体的实现步骤叙述如下:
(1)生成VIRGINIA的训练数据,如图 2所示.对采集的ACS低分辨率数据,应用VCC方法,即(5)式获得两个训练数据样本.在频率编码/读出方向上连接每一个图像层,然后经过傅里叶变换到k空间,获得大小为[Ns, Npe, Nfe×MB, Nc]的完整k空间数据(如图 2橙色方框中所示);
(2)基于VIRGINIA的模型训练,如图 3所示.对于步骤(1)中得到的完整k空间的复数数据,将其虚数部分连接在线圈方向上,并根据图 3(b),以MB倍的加速因子沿着读出方向降采样该数据,分别获得大小为[Ns, Npe, Nfe, 2Nc]和[Ns, Npe, Nfe, 2Nc, (MB-1)]的训练输入和输出数据.为便于处理,将输出数据的(MB-1)份数据扩展到线圈方向上变为大小为[Ns, Npe, Nfe, 2Nc× (MB-1)]的输出;
(3)生成各层k空间数据.将采集的MB倍片层加速的SMS混叠数据输入到步骤(2)中训练好的双层CNN网络得到大小为[1, Npe, Nfe, 2Nc×(MB-1)]的输出,按照图 3(b)的方式将输入和输出在读出方向上以步骤(2)的逆过程方式融合,即沿着读出方向插值输入和输出数据,从而获得重建的SMS的k空间数据;
(4)重建SMS各层图像.将步骤(3)重建的SMS的k空间数据经过逆傅里叶变换后做线圈的平方和融合,获得有片层间偏移的各层图像(图 1),经过偏移校正后即获得最终的多层图像.
2 实验部分 2.1 实验数据本文采用基于文献[19]报道的多回波偏移技术结合加速的GRE序列(简称为SMSiES技术,可用于同时多平面激发成像数据采集)进行MRI数据采集.该技术在一个有效重复时间(Repetition Time,TR)内同时激发多个片层,应用交错的片层采集方案,结合回波偏移技术,避免了信号损失,而且不影响采集速度;同时也应用CAIPIRINHA技术来增加线圈敏感度的差异性,从而更准确地分离各个层信号.本文数据采自西门子7T MRI系统(MAGNETOM Tim Trio, Siemens AG,Erlangen,Germany),使用32通道头部线圈.扫描对象是一名有MRI实验经历的健康志愿者,并签署了本地的机构伦理审查委员会的知情同意书.扫描部位为头部,采集参数如下:脉冲翻转角为9˚,有效回波时间为24.4 ms,有效TR为27.6 ms,体素大小为1.0×1.0×2.5 mm3,成像矩阵大小为192×192,采集带宽为389 Hz/pixel,GRAPPA加速倍数为2倍,SMS加速倍数为5倍,即MB=5.其中5个层之间的相位偏移距离是[0, π/2, 0, π/2, 0].
基于上述方案采集的3份MB=5的头部SMS数据作为参考数据,实现不同层加速的SMS数据仿真.仿真SMS数据时,各层之间FOV偏移距离设为FOV/MB,回溯降采样了2、3、4、5和15倍层加速下的五组数据.其中,在5倍加速下每个层取20条ACS线,在15倍加速下取60条ACS线,其余情况各取15条中心ACS线.这五组数据分别使用了SG、RAKI和VIRGINIA三种重建方法进行重建.
为了验证算法结果的稳定性,本文对上述2、3和4倍层加速的三组数据分别添加随机生成的高斯白噪声,生成三组64份带噪声的SMS数据,并用VIRGINIA方法和RAKI方法分别进行重建并计算PSNR、SSIM和RMSE.
2.2 实验平台及参数设置本文所有实验均在一台服务器上完成,此服务器配置如下:2个Intel Xeon CPUs,型号为ES-2660(10 cores each,2.6 GHz),125 GB内存,2个GPU(Quadro K4200 GPU和Tesla K40 GPU),系统是Linux 4.5.0(Ubuntu 16.04.3 LTS),编译器是GCC5.4.0.其中,RAKI和VIRGINIA的网络训练和重建均使用Python 3.6.8和TensorFlow 1.13.1实现,并由CUDA 8.0.61和CuDNN 7.0.5支持.此处,Python环境由Anaconda 5.3.1创建.所有方法的最终数据后处理和图像评价指标计算,以及SG重建计算均在MATLAB 2015a计算平台(MathWorks Inc.)中完成.
本文对SG、RAKI与VIRGINIA方法在MB为2、3、4、5和15时进行了比较.为方便比较,RAKI和VIRGINIA网络中的所有实验参数都一致.使用ADAM优化器,MAE损失函数,ReLu激活函数,学习率设置为0.001,并且以指数形式衰减,样本训练次数(Epoch)为1 500.两层卷积核w1和w2的尺寸分别由加速因子决定,一般情况下分别是[5, 3]和[2, 2].第二层的输出通道数目为[(MB-1)·2L];第一层的输出通道数和第二层相等;SG方法中使用的卷积核大小均为[3, 3].
需要注意的是,尽管CNN中没有学习偏置项,但是k空间信号在RAKI网络中还是引入了比较小的直流偏量,具体表现即图像中心会存在一个比较亮的信号,因此将数据输入网络前,需要在k空间读出方向上做一个FOV/2的相位偏移,重建完毕后再偏移回来,从而将该亮信号从目标区域移除.而且在读出方向上做该相位偏移也不会影响到CAIPIRINIHA采集上相位编码方向的相位变化[20].
3 结果与讨论 3.1 结果本文使用SG、RAKI和VIRGINIA三种重建方法,分别对MB=2、3、4、5和15倍片层加速下的SMS混叠数据做了重建,并计算了每层重建图像的性能评价指标(包括PSNR、SSIM和RMSE),表 1对应记录了MB层重建图像的性能评价指标的平均值.其中,表 1计算VIRGINIA方法相对于另外两种方法SG和RAKI的提升百分比时,先对重建的每层图像计算提升百分比(如,VIRGINIA方法相对于RAKI方法在PSNR下的提升百分比为PSNR_percent=(PSNR_VIRGINIA – PSNR_RAKI)/ PSNR_RAKI),然后对MB层重建图像的提升百分比计算值取平均.
| 表 1 不同加速倍数下,利用SG、RAKI和VIRGINIA三种重建方法重建性能的比较 Table 1 Comparison among the reconstruction performances acquired using SG, RAKI and VIRGINIA methods |
根据经验,为获得更好的重建结果,加速倍数增大时需要适度增大卷积核.从表 1可以看出,相对于传统的SG重建方法,基于CNN网络的方法获得的PSNR、SSIM和RMSE测度指标都有显著的性能提升,而且本文提出的VIRGINIA性能优于RAKI.
图 4~7分别给出了MB=2、3、4和5时用SG、RAKI和VIRGINIA方法重建的误差图像,图S1~S4(扫描文章首页OSID码,或者在文章网络版查看附件)给出了对应加速倍数下的三种方法的重建图像的相应参考图像,其中,所有的重建图像均被归一化后显示,误差图像的色度范围在[0, 0.2].结果显示,RAKI方法与VIRGINIA方法均优于传统的SG重建方法.比较MB=2、3和4倍层加速下RAKI和VIRGINIA的重建结果,发现在相同网络参数下,虚拟共轭线圈的引入明显改善了重建图像的质量.由图 7和图 8以及补充材料中的图S4和图S5可看出,在更高倍加速(MB=5和15)下,虽然VCC技术相对于SG和RAKI获得了更优的重建结果,但重建图像的整体误差较大,这也是VCC技术所存在的局限.

|
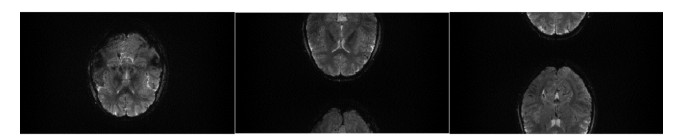
图 4 2倍层加速下,VIRGINIA、RAKI与SG的SMS图像重建误差图.每张图下方的三个数值是由重建图与参考图像计算的PSNR/SSIM/RMSE Fig. 4 The error maps between reference and reconstructed images with VIRGINIA, RAKI and SG approaches under acceleration factor of 2. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |
|
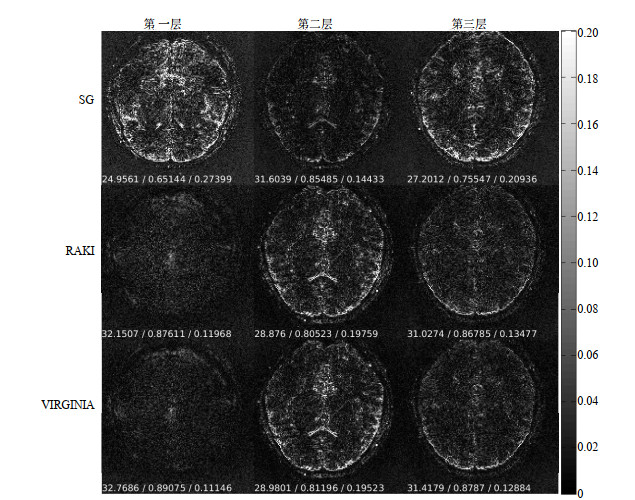
图 5 3倍层加速下,SG、RAKI与VIRGINIA的SMS图像重建误差图.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE Fig. 5 The error maps between reference and reconstructed images with SG, RAKI and VIRGINIA approaches under acceleration factor of 3. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |
|
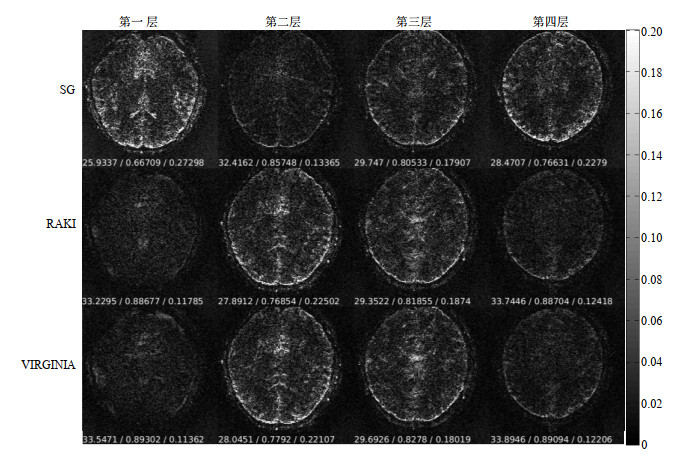
图 6 4倍层加速下,SG、RAKI与VIRGINIA的SMS图像重建误差图.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE Fig. 6 The error maps between reference and reconstructed images with SG, RAKI and VIRGINIA approaches under acceleration factor of 4. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |
|
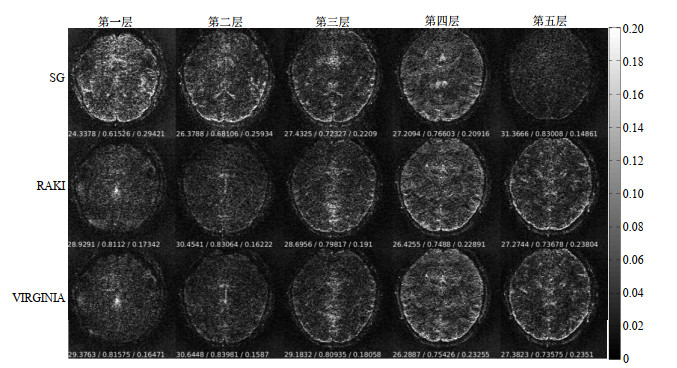
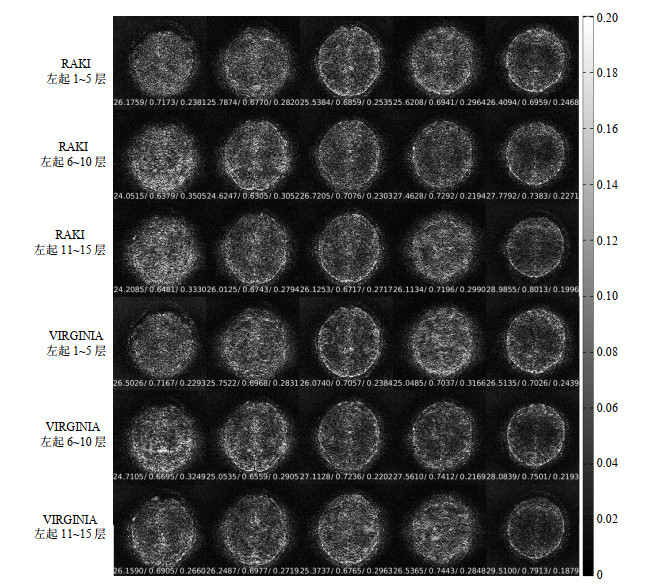
图 7 5倍层加速下,SG、RAKI与VIRGINIA的SMS图像重建误差图.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE Fig. 7 The error maps between reference and reconstructed images with SG, RAKI and VIRGINIA approaches under acceleration factor of 5. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |
|
图 8 15倍层加速下,RAKI与VIRGINIA的SMS图像重建误差图.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE Fig. 8 The error maps between reference and reconstructed images with RAKI and VIRGINIA approaches under acceleration factor of 15. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |
为了验证VIRGINIA方法相对于RAKI方法的提升显著性,本文对64份含高斯噪声的加速数据做了重建,图S6~8分别是2、3和4倍片层加速下使用VIRGINIA方法和RAKI方法计算的PSNR、SSIM和RMSE的曲线图.可以看到,VIRGINIA方法的PSNR、SSIM和RMSE计算结果稳定地好于RAKI方法,而图S8的4倍层加速下的VIRGINIA方法只有SSIM仍好于RAKI方法,因此,更高的加速倍数下,VCC技术对SMS重建图像的提升效果会有一定的局限性.
观察图 4~6可以发现,在2、3和4倍加速时,基于卷积网络的RAKI和VIRGINIA重建方法获得的第一层和最后一层的重建图像的质量明显好于中间片层,而基于SG方法的重建情况却相反,但即使如此,基于神经网络的RAKI和VIRGINIA重建方法整体上仍然优于SG方法;在5倍和15倍加速时(图 7和图 8),此现象存在,但不是特别明显,造成该现象的原因目前还不是很清楚,需要进一步研究.
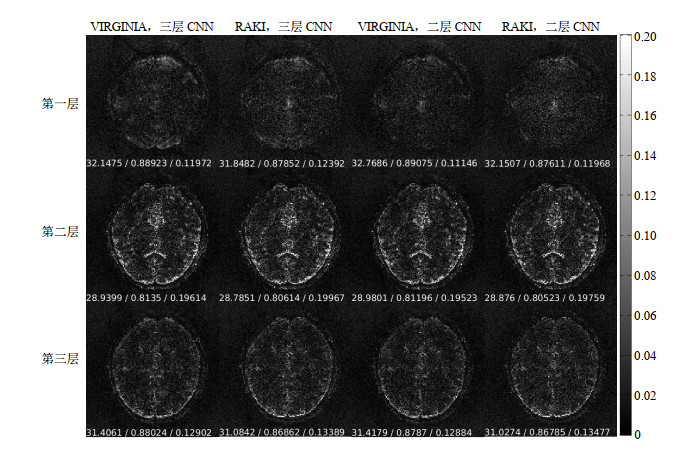
3.2 讨论分析 3.2.1 网络参数及相关函数的选择原始的RAKI使用的是基于三层CNN的磁共振图像重建方法,本文在增加了虚拟训练的基础上不断测试观察,发现二层CNN的重建结果稍好于三层,同时因为网络层数和网络参数的减少,高倍加速下的训练时间也相应有所减少,因此,本文选择二层CNN进行重建.以3倍和4倍层加速的SMS图像重建为例,三层和二层CNN下的重建结果如图 9和图 10所示.从重建误差图和PSNR、SSIM、RMSE数值中可以观察到:3倍层加速下,VIRGINIA方法在二层CNN下的重建性能稍好于三层,而RAKI方法在三层和二层下的结果差异不大,4倍层加速下类似;同时,三层CNN下和二层CNN下,3倍层加速时,VIRGINIA的重建性能均优于RAKI,而4倍层加速下,三层CNN的VIRGINIA的重建性能与RAKI不相上下,二层CNN的VIRGINIA的重建性能稍微好于RAKI.综合上述分析,选择基于二层CNN网络的VIRGINIA和RAKI重建方法具有更佳的重建结果.
|
图 9 3倍层加速下,比较VIRGINIA和RAKI在三层和二层CNN下的重建误差.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE Fig. 9 The error maps between reference and reconstructed images with VIRGINIA and RAKI approaches under 3-layer and 2-layer CNNs at acceleration factor of 3. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE |

|
图 10 4倍层加速下,VIRGINIA和RAKI在三层和二层CNN下的重建误差.每张图下方的三个数值是由重建图与参考图计算的PSNR/SSIM/RMSE
Fig. 10 The error maps between reference and reconstructed images with VIRGINIA and RAKI approaches under 3-layer and 2-layer CNNs at acceleration factor of 4. The three values at the bottom of each map are the corresponding PSNR/SSIM/RMSE
|
由于磁共振的k空间数据是复数,而CNN网络只能处理实数数据,将复数虚部连接到线圈方向,因此第一层网络输入通道数目为2倍的线圈数目,第二层网络输出通道数目为2倍的(MB-1)×Nc,第一层网络输出通道数和第二层网络的输出通道数目设置相同.
调参过程中,Epoch数目增加到一定程度,如5 000时,会产生过拟合.通过观察训练下降曲线,我们认为Epoch数目在3 000以内,重建结果较为理想,因此本文所有方法中,Epoch数目均取值为1 500.
第二层卷积核大小设为[2, 2]、[3, 2]或[3, 3],第一层卷积核在[3, 3]的基础上随着加速倍数增大而逐步适当增加,从而改善重建结果.
为了提升网络的表现能力,需要引入非线性激活函数.相比Sigmoid,ReLu激活函数不存在训练时梯度消失问题,而且运算简单、速度快,因此,本文使用ReLu非线性激活函数.
损失函数是为了最小化真实标签数据和网络预测数据之间误差,一般可以选择均方误差(Mean Square Error,MSE)和平均绝对值误差(Mean Absolute Error,MAE).最小化MSE得到是所有样本点预测值的平均值,最小化MAE得到的则是所有预测值的中位数.当标签值和预测值很接近,即误差很小时,计算得到的MSE和MAE值都较小;而当存在异常预测值时,因为计算MSE时有平方运算,得到的MSE值的对异常点加权的权重更大,因此MAE比MSE更鲁棒.MAE函数如(7)式所示,由真实数据
| $MAE = \sum\limits_i^N {\left| {{y_i} - y_i^{output}} \right|} $ | (7) |
本文使用VCC方法时,其数据扩展方式区别于传统的重建算法.传统的线性重建方法是将扩展的VCC数据连接到线圈方向上,便于在线性重建核中包含所生成虚拟数据的信息.在线圈方向上扩展数据会增加网络的参数量和训练时间.本文提出的VIRGINIA方法在基于神经网络的训练过程中可以从额外增加的训练样本中有效提取生成的虚拟数据的可利用信息,从而得到和在线圈方向扩展相似的结果,但是没有增加训练时间.而且在实际实验时,我们还发现即使在线圈方向上引入VCC扩展的重建结果,并不比VIRGINIA的重建结果更为有效.
4 结论本文通过引入VCC,提出了一种基于CNN的SMS图像重建方法,将其命名为VIRGINIA.其利用k空间信号的复数共轭对称性质生成虚拟共轭数据,从而扩展了训练数据集、增加了训练样本,并更加充分地利用了线圈部分的相位信息;同时,通过利用MRI数据的复数共轭对称性和构造卷积网络实现了快速SMS图像重建,并得到了比传统并行重建方法更高质量的重建图像.
| [1] |
ZHENG H R, WU Y, HE Q, et al. Fast and high-resolution magnetic resonance imaging on high field system[J].
Life Science Instruments, 2018, 16(Z1): 29-44, 54.
郑海荣, 吴垠, 贺强, 等. 基于高场磁共振的快速高分辨成像[J]. 生命科学仪器, 2018, 16(Z1): 29-44, 54. |
| [2] | MCGIBNEY G, SMITH M R, NICHOLS S T, et al. Quantitative-evaluation of several partial fourier reconstruction algorithms used in MRI[J]. Magn Reson Med, 1993, 30(1): 51-59. DOI: 10.1002/mrm.1910300109. |
| [3] | PRUESSMANN K P, WEIGER M, SCHEIDEGGER M B, et al. SENSE:Sensitivity encoding for fast MRI[J]. Magn Reson Med, 1999, 42(5): 952-962. DOI: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S. |
| [4] | GRISWOLD M A, JAKOB P M, HEIDEMANN R M, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA)[J]. Magn Reson Med, 2002, 47(6): 1202-1210. DOI: 10.1002/mrm.10171. |
| [5] | SETSOMPOP K, GAGOSKI B A, POLIMENI J R, et al. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty[J]. Magn Reson Med, 2012, 67(5): 1210-1224. DOI: 10.1002/mrm.23097. |
| [6] | LARKMAN D J, HAJNAL J V, HERLIHY A H, et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited[J]. J Magn Reson Imaging, 2001, 13(2): 313-317. DOI: 10.1002/1522-2586(200102)13:2<313::AID-JMRI1045>3.0.CO;2-W. |
| [7] | BREUER F A, BLAIMER M, HEIDEMANN R M, et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging[J]. Magn Reson Med, 2005, 53(3): 684-691. DOI: 10.1002/mrm.20401. |
| [8] | NUNES R G, HAJNAL J V, GOLAY X, et al. Simultaneous slice excitation and reconstruction for single shot EPI[C]//14th Annual Meeting of ISMRM, Seattle, Washington, USA. 2006: 293. |
| [9] | CHENG J, WANG H, YING L, et al. Model learning: Primal dual networks for fast MR imaging[C]. International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Oct. 13-17, 2019, Shenzhen, China. Springer, Cham, 2019: 21-29. |
| [10] | WANG H, CHENG J, JIA S, et al. Accelerating MR imaging via deep Chambolle-Pock network[C]. 201941st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jul. 23-27, 2019, Berlin, Germany. IEEE, 2019: 6818-6821. |
| [11] |
CHENG H T, WANG S S, KE Z W, et al. A deep recursive cascaded convolutional network for parallel MRI[J].
Chinese J Magn Reson, 2019, 36(4): 437-445.
程慧涛, 王珊珊, 柯子文, 等. 基于深度递归级联卷积神经网络的并行磁共振成像方法[J]. 波谱学杂志, 2019, 36(4): 437-445. |
| [12] |
WANG H Z, ZHAO D, YANG L Q, et al. An approach for training data enrichment and batch labeling in AI+MRI aided diagnosis[J].
Chinese J Magn Reson, 2018, 35(4): 447-456.
汪红志, 赵地, 杨丽琴, 等. 基于AI+MRI的影像诊断的样本增广与批量标注方法[J]. 波谱学杂志, 2018, 35(4): 447-456. |
| [13] | AKCAKAYA M, MOELLER S, WEINGAERTNER S, et al. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction:Database-free deep learning for fast imaging[J]. Magn Reson Med, 2019, 81(1): 439-453. DOI: 10.1002/mrm.27420. |
| [14] | EO T, JUN Y, KIM T, et al. KIKI-net:cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images[J]. Magn Reson Med, 2018, 80(5): 2188-2201. DOI: 10.1002/mrm.27201. |
| [15] | BLAIMER M, BREUER F A, SEIBERLICH N, et al. Accelerated volumetric MRI with a SENSE/GRAPPA combination[J]. J Magn Reson Imaging, 2006, 24(2): 444-450. DOI: 10.1002/jmri.20632. |
| [16] | ZHANG C, MOELLER S, WEINGAERTNER S, et al. Accelerated simultaneous multi-slice MRI using subject-specific convolutional neural networks[C]. Conference Record of the Asilomar Conference on Signals Systems and Computers, Pacific Grove, CA. 2018: 1636-1640. |
| [17] | BLAIMER M, GUTBERLET M, KELLMAN P, et al. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals[J]. Magn Reson Med, 2009, 61(1): 93-102. DOI: 10.1002/mrm.21652. |
| [18] | KINGMA D P, BA J. Adam: A method for stochastic optimization[C]. International Conference on Learning Representations (ICLR), May 7-9, 2015, San Diego, USA. arXiv preprint arXiv: 1412.6980, 2014. |
| [19] | SU S, LU N, JIA L, et al. High spatial resolution BOLD fMRI using simultaneous multislice excitation with echo-shifting gradient echo at 7 Tesla[J]. Magnc Reson Imaging, 2020, 66: 86-92. DOI: 10.1016/j.mri.2018.08.019. |
| [20] | MICKEVICIUS N J, PAULSON E S, TUGAN MUFTULER L, et al. Application of a k-space interpolating artificial neural network to in-plane accelerated simultaneous multislice imaging[OL].[2019-02-01]. https://ui.adsabs.harvard.edu/abs/2019arXiv190208589M |
 2020, Vol. 37
2020, Vol. 37 
