引言

扩散张量成像（Diffusion Tensor Imaging，DTI）作为磁共振成像（Magnetic Resonance Imaging，MRI）的一种，可以无创地量化水分子在体内的自由扩散，以获取人体组织的结构或功能信息，从而进一步进行如人脑白质纤维追踪^[1-3]、配准^{[4, 5]}和脑图谱构建^[6-8]等的研究.张量可以定义为3×3对称正定矩阵^[9]，该矩阵可以用椭球体表示，其3个对称轴的方向和大小分别是张量的特征向量和特征值，即扩散张量的形状和方向可以通过张量的特征值和特征向量表示.这些扩散张量可以用来表示体内各向异性纤维组织以及器官的纤维结构特征，且张量包含方向、扩散的各向异性，以及扩散系数等定量化的微结构信息，这对于临床医学分析具有重要价值.然而，由于采集图像时的技术限制，DTI数据的分辨率通常较低，如心脏的心肌部分是稀疏且不连续的，这对于临床分析会产生较大的误导，因此需要提高图像插值分辨率.此外，在一些应用中，如人脑白质纤维追踪^[1-3]、配准^{[4, 5]}和DTI脑模板构建^[6-8]等方面都需要对图像进行张量插值从而得到像素点之间的信息，因此DTI插值是一个非常重要的图像处理步骤.扩散张量图像插值是利用已知采样点的张量来产生未知点的张量的过程，从而由低分辨率图像生成高分辨率图像^[10].

经典的张量插值方法是通过用欧几里德框架将张量信息转换成标量数据^[11-13].在医学图像配准中，基于欧几里德框架的标量插值方法已广泛应用于临床^{[14, 15]}，但并不能保证张量的正定性和不变性^[16].为了解决这个问题，研究者把黎曼几何中的仿射不变度量、对数欧几里德（Log Euclidean，Log-E）度量和黎曼对称空间（Riemannian Symmetric Space，RSS）度量这几个概念引入张量场，通过对张量空间用黎曼度量变换为黎曼流形，最终在流形上进行张量插值^{[17, 18]}.然而，基于黎曼框架的插值方法总是生成固定的行列式轮廓，而固定的行列式轮廓不能适应生物组织中的各种扩散模式.因此，一些研究者^[19]又提出了基于黎曼测地线上非均匀运动的轮廓控制方法，该方法能够使用一个任意单调轮廓，如线性轮廓、黎曼轮廓以及正弦轮廓等，代替固定轮廓，使得最终插值结果可以随着生物组织扩散模式的特性而改变.虽然这些插值方法能够保证张量行列式的单调变化以避免膨胀效应，但忽略了张量性质的单调性.值得注意的是，扩散张量具有张量形状和张量方向的两个特征.张量的形状大小可以通过三个特征值表示，方向是由三个欧拉角^[20]或单位四元数^[21]表示.通过特征值和欧拉角或四元数插值法重新构造待插值的张量，这不仅保留了黎曼几何插值的轮廓非固定性，而且保留了张量的对称正定性，同时又保持了部分各向异性（Fractional Anisotropy，FA）和平均扩散率（Mean Diffusivity，MD）等扩散特性的单调性.

总体而言，目前的张量图像插值方法根据不同的空间几何框架可以划分为三大类：1）基于欧几里德空间的张量图像插值方法，主要思想是对欧几里德空间中扩散张量的每个矩阵分量进行独立插值，或者对张量进行分段插值，更进一步的是对张量进行参数化约束，以保持扩散张量的对称正定性；2）基于黎曼几何的张量图像插值方法，主要思想是把张量空间变换为黎曼流形，最终在流形上进行插值；3）基于欧拉角或四元数的图像插值方法，主要思想是根据不同的张量特性权重因子对张量矩阵获取的特征值和特征向量进行插值.

本文主要对现有的张量插值方法进行综述，第一部分详细介绍各种张量插值方法的理论基础，阐述张量插值方法中所需解决的技术问题及存在的局限性；第二部分将介绍常用的插值评估指标；第三部分根据现有的典型插值方法进行仿真数据和真实数据实验，并分析总结；第四部分是对张量插值的未来发展趋势提出建议.

1 张量插值方法

扩散张量是一个对称正定矩阵，可以定义为

$D = \left( {\begin{array}{*{20}{c}} {{D_{xx}}}&{{D_{xy}}}&{{D_{xz}}} \\ {{D_{xy}}}&{{D_{yy}}}&{{D_{yz}}} \\ {{D_{xz}}}&{{D_{yz}}}&{{D_{zz}}} \end{array}} \right)$

(1)

其中，${D_{xx}}$、${D_{yy}}$和${D_{zz}}$分别是x、y和z方向上的扩散流动量.假设给定两个已知采样点的张量是${D_1}$和${D_2}$，且${D_1} > 0$、${D_2} > 0$.若计算两个采样点之间的任意插值张量，对于一维情况，张量插值和标量插值一致，两个采样点之间的插值空间可以定义为一个时域函数$v(t)$，$t \in [0, 1]$：时间$t = 0$时，$v(0)$的取值为张量${D_1}$；时间$t = 1$时，$v(1)$的取值为张量${D_2}$.因此，只需要计算时域函数内的$v(t)$就能获取插值张量$D(t), $$t \in [0, 1]$.对于二维情况，此时曲面四个角分别为四个张量，张量插值问题定义为对该曲面插值.下面主要根据不同的几何空间框架，先简要介绍各张量插值方法的理论基础，再重点分析这些方法中所需解决的技术问题及存在的局限性.

1.1 基于欧几里德空间的张量图像插值方法

直观而言，张量可以定义为欧几里德空间中的矩阵，通过矩阵在欧几里德空间中的计算框架能够处理张量的插值问题.一维情况下，一个张量D映射成一个六维向量$v = ({d_{11}}, {d_{12}}, {d_{22}}, {d_{33}}, {d_{13}}, {d_{23}})$，时间$t \in [0, 1]$，此时张量插值表示为

$v(t) = (1 - t){v_1} + t{v_2}$

(2)

其中，$v(t)$是待插值张量，${v_1}$和${v_2}$分别是两个张量${D_1}$和${D_2}$的六维向量.

同时，根据欧几里德空间的计算框架，两个张量${D_1}$和${D_2}$之间的欧几里得距离定义为

$dist({D_1}, {D_2}) = \sqrt {trace[{{({D_1} - {D_2})}^2}]} $

(3)

张量矩阵本身不是由MRI扫描仪直接采集而来，而是由多个具有不同方向扩散和编码梯度的扩散加权图像计算得到的.因此，Kindlmann等^{[11, 12]}认为对原始扩散加权图像进行插值是最有效的方法，他们把采集的扩散加权图像分解为6个扩散加权标量图像的通道，每个通道对应于在扫描获取期间使用的一对梯度编码方向，然后对标量图像进行线性插值.插值重建的结果显示，基于原始数据进行通道分解的线性插值方法得到的最终插值张量与实际张量明显不同.该方法导致张量场的边界过平滑，并且插值过程中无法避免地产生负定张量，这与定义的正定张量是不一致的.

由于对称张量在张量空间中形成线性子空间，对称张量的任何线性组合仍然是对称张量，即在线性组合下对称张量是闭合的.为此，Zhukov等^[13]认为可以使用三分段线性插值插值重建图像中的连续张量场，其中体素内任意点的张量值是顶角上的8个值的线性组合：

$\begin{array}{l} D(x, y, z) = {D_{i, j, k}}(1 - x)(1 - y)(1 - z) + {D_{i + 1, j, k}}x(1 - y)(1 - z) + {D_{i, j + 1, k}}(1 - x)y(1 - z) \\ {\rm{ }} + {D_{i, j, k + 1}}(1 - x)(1 - y)z + {D_{i + 1, j, k + 1}}x(1 - y)z + {D_{i, j + 1, k + 1}}(1 - x)yz \\ {\rm{ }} + {D_{i + 1, j + 1, k}}xy(1 - z) + {D_{i + 1, j + 1, k + 1}}xyz \\ \end{array} $

(4)

其中，$(x, y, z)$是待插值点，$D(x, y, z)$表示待插值点的张量，$(i, j, k)$表示待插值点相邻体素的坐标，${D_{i, j, k}}(x, y, z)$是待插值点相邻体素的张量.

这种思想适用于灰度图像，可以直接应用于欧几里德几何的矩阵中，虽然这种直观的欧几里德插值方法比较简单，但仍存在两个问题：非正定效应和膨胀效应.

为了解决欧几里德空间张量插值方法带来的非正定性问题，Wang等^[22]提出使用Cholesky因子分解对张量进行参数化，以保持扩散张量的对称正变性.研究者们提出了一种新的约束变分原理公式，用于平滑和估计扩散加权图像的张量插值.这是通过脉冲梯度自旋回波序列（Pulse Gradient Spin Echo Sequence，PGSE）的扩散权重成像公式——Stejskal-Tanner方程获取原始数据，也是第一次通过这种方法平滑并估计正定扩散向量场，利用Cholesky分解估计出扩散张量的正定性约束，然后通过改进的拉格朗日方法，将约束变分原理公式转化为无约束问题序列，并进行了数值求解.

然而，在应用Cholesky因子分解插值张量时，可以保证插值张量是对称正定矩阵，但是张量的特征系数FA和MD有所降低.FA反映测量不同方向的水迁移率的变异性，MD是测量与方向无关的平均扩散率.这是临床分析中广泛使用的两个重要参数.在大脑扩散张量图像中，FA和MD通常用于定位其他临床MRI形式中无法显示出的白质病变.FA的减少可能是因为白质纤维组织的崩塌^[23]、白质与年龄有关的恶化^[24]和多发性硬化症^[25]或精神分裂症^[26]的出现，而FA的减少也可能影响完整的白质的特殊结构性质，比如交叉或吻合的纤维^[27]，以及纤维密度的差异性^[28].Chao等^[29]指出，在空间归一化过程中的张量插值可能以不可忽略的程度降低FA值，并使得临床难以区分正常组和异常组，尤其是右侧大脑前冠状.对于心脏DTI，FA和MD在区分正常与梗死区方面也起重要作用.一些试图研究量化心肌梗死发生后的心室重构^[30]的研究中发现，FA的减少和MD的增加是明显的，这被认为是与细胞死亡一致的梗死区域^[30].换而言之，大脑中FA的减少可能是由于疾病或跨界引起的，而心脏中FA的减少则是由梗死引起的.基于以上这些原因，插值引起的FA的减少可能会误导临床分析诊断的结果.

1.2 基于黎曼几何的张量图像插值方法

为了在消除膨胀效应的同时，保持扩散张量的正定性，研究者提出了在黎曼空间进行插值的方法^{[17, 31, 32]}.扩散张量矩阵的本质特征是其所有特征值为正.然而，欧几里德插值方法推导的算子对于正定张量并不特殊，特征值为0或负值的张量却与正定张量处理方式相同.

1.2.1 仿射不变黎曼几何插值

黎曼张量空间是一个规则的流形，相比于向量空间，黎曼张量空间无法使用一般的加性运算.当进行张量场估计时，在标准DTI中，估计的对称矩阵可能具有负的特征值，或者当平滑张量场时，等特征值附近也存在连续性问题.因此，Pennec等^[17]研究了仿射不变量框架内的偏微分方程，首次在张量空间中引入仿射不变黎曼度量，使得张量空间成为黎曼流形.当$t \in [0, 1]$时，仿射不变黎曼几何插值方法定义为

$D(t) = D_1^{\frac{1}{2}}\{ \exp [t\ln (D_1^{ - \frac{1}{2}}{D_2}D_1^{ - \frac{1}{2}})]\} D_1^{\frac{1}{2}}$

(5)

(5) 式中，${D_1}$和${D_2}$分别是起始点张量和终点张量.

这是仿射不变黎曼框架首次应用于DTI插值.仿射不变几何是3×3正定矩阵齐次空间${S^ + }(3)$的自然几何度量，在统计和凸优化中也起着重要的作用^[33].然而，如果对于规则采样张量，如线性或三线性插值，该方法容易定义权重，但对于不规则采样张量却很困难.

1.2.2 黎曼对称空间插值

相比于线性空间，扩散张量空间描述为RSS比较自然.在之前的相关研究中，Fletcher等^[31]引入了主测地线分析（Principal Geodesic Analysis，PGA）代替主成分分析，以研究李群数据的统计变异性.后来，他们将这些思想扩展到对称空间，提供了计算平均值和描述扩散张量数据可变性的新方法.研究证明，这些统计量保留了扩散张量的自然性质，最重要的是正定性，但是线性统计量并没有保留这些性质.基于对称空间公式，当$t \in $[0, 1]时，RSS方法^[32]定义为

${D_{{\rm{RSS}}}}(t) = (gv)[\exp (t\mathit{\Sigma} )]{(gv)^{\rm{T}}}$

(6)

其中g、v和Σ是张量${D_1}$和${D_2}$导出的李群作用对称矩阵.

该方法是根据Batchelor等^[34]提出的测地线插值以及旋转插值方法改进而来.测地线插值描述了用于平均任意数量的张量、测地线各向异性和两个扩散张量之间的插值的对称空间几何：

${D^t} = R{\mathit{\Lambda} ^t}{R^{\rm{T}}} = Rdiag(\lambda _i^t){R^{\rm{T}}}$

(7)

其中，Λ是特征值的对角矩阵，R是特征向量的正交矩阵，λ表示特征值.

然而，研究者自己意识到，这种方法是根据张量的特征值进行插值的.特征值只能反映张量的形状大小，却忽略了张量的方向，因此他们又把测地线插值修改为旋转插值.对称张量可以通过旋转实现对角化，并且旋转矩阵可以用特征值插值时相同的方式进行插值：

$\begin{array}{l} R(t) = {R_1}{(R_1^{\rm{T}}{R_2})^t} \\ D(t) = R(t)\mathit{\Lambda} _1^t\mathit{\Lambda} _2^{1 - t}R{(t)^{\rm{T}}} \\ \end{array} $

(8)

其中，$R(t)$为旋转插值矩阵，${R_1}$、${R_2}$分别是${D_1}$和${D_2}$的旋转矩阵.

因此，RSS度量中的方法可以用于计算张量之间的测地线距离、张量集的加权平均值等，两个张量${D_1}$和${D_2}$间的黎曼距离计算为：

$dist({D_1}, {D_2}) = \sqrt {trace[{{(\ln \mathit{\Sigma} )}^2}]} $

(9)

相比而言，RSS方法更进一步，不仅首次在对称空间框架中描述二阶统计量，即协方差和变化模式，而且可以处理任意数量的张量，而不是局限于只能两个张量的情况.然而，RSS方法虽然具有稳定的理论基础，但计算过于复杂.

1.2.3 对数欧几里德黎曼插值

为了降低算法的计算成本，Arsigny等^[35]提出一种基于log-E度量的张量插值方法.该方法使用矩阵对数定义${S^ + }(3)$的全局嵌入到对称矩阵的（线性）空间中，即利用矩阵空间对数映射将非线性空间${S^ + }(3)$映射到线性空间，log-E插值定义为

${D_{{\rm{log - E}}}}(t) = \exp [(1 - t)\ln {D_1} + t\ln {D_2}]$

(10)

两张量${D_1}$和${D_2}$间的黎曼距离计算为

$dist({D_1}, {D_2}) = \sqrt {trace[{{(\ln {D_1} - \ln {D_2})}^2}]} $

(11)

研究证明，由于log-E方法的计算优势超过仿射不变黎曼几何插值以及RSS插值，所以它是常用的DTI插值方法.实际上，对数欧氏几何是非特征的，与仿射不变量相反.外在几何在接近于同一性时产生内在的一个良好的近似，但近似的质量在远离它时减小.

1.2.4 基于黎曼测地线的轮廓控制插值

虽然RSS插值方法和log-E方法使用的距离度量不相同，但是它们的待插值张量轮廓是相同的.如果基于黎曼框架的插值方法进行插值，生成的行列式轮廓则是固定的，但是生物组织的扩散张量行列式轮廓可能会随着生物不同而发生变化.因此，固定的行列式轮廓并不能满足所有张量插值的需要^[36].

为了解决这个问题，Son等^[19]认为黎曼方法中的插值是通过求时域函数$v(t)$，即两张量之间黎曼测地线的均匀运动进行的，所以才会生成相同的行列式轮廓.如果插值时间系数t修正为$f(t)$，即插值在运动方向上进行非均匀运动，那么就能够在不影响插值正定性和行列式单调性的情况下控制插值的行列式轮廓.因此，插值行列式轮廓修正为$\det \{ {D_{Ri}}[f(t)]\} $，其中$f(t)$表示为

$f(t) = \frac{{\ln [\psi (t)/a]}}{{\ln (b/a)}}$

(12)

其中，$a = \det {D_1}$；$b = \det {D_2}$；$\psi (t)$是插值轮廓，常用的插值轮廓有黎曼轮廓、线性轮廓以及正弦轮廓等.

然而，经研究证明，对于医学扩散张量图像，研究者使用基于黎曼测地线轮廓控制的插值方法能一定程度控制张量行列式的插值变化，可以适当地缩小插值误差，抑制膨胀效应.但该方法在工程方面大范围使用的欧氏误差度量下并不存在优势.因此，甄帅等^[37]引入张量局部特征，待插值点根据相邻4个张量各自沿x, y轴方向相邻张量的空间距离来进行局部特征的权重修正，从而进一步优化插值结果.

1.3 基于欧拉角或四元数插值 1.3.1 基于张量形状的插值

扩散张量图像处理时通常不使用基于黎曼几何的插值方法，主要是因为计算量太大.基于黎曼测地线的轮廓控制插值方法中所涉及的处理步骤是必须使用矩阵指数和矩阵对数来处理张量，导致DTI数据计算量很大.为了提高计算效率，研究者们尝试把矩阵张量转化为特征值和特征向量表示，通过对特征值和特征向量进行系统地插值来降低计算成本.

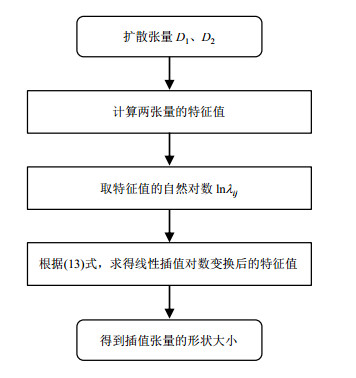
为了避免膨胀效应，扩散张量行列式必须被单调插值^[35].因此，研究者不能直接插值特征值，因为这不能保证行列式的单调性.解决方法是取特征值的自然对数，然后线性地插值这些对数变换后的值，如图 1，因而插值张量的大小产生了以下映射：

${\lambda '_{i1}} = t\ln {\lambda _{11}} + (1 - t)\ln {\lambda _{21}} = \ln (\lambda _{11}^t\lambda _{21}^{1 - t})$

${\lambda '_{i2}} = t\ln {\lambda _{12}} + (1 - t)\ln {\lambda _{22}} = \ln (\lambda _{12}^t\lambda _{22}^{1 - t})$

(13)

${\lambda '_{i3}} = t\ln {\lambda _{13}} + (1 - t)\ln {\lambda _{23}} = \ln (\lambda _{13}^t\lambda _{23}^{1 - t})$

其中，$\{ {\lambda _{11}}, {\lambda _{12}}, {\lambda _{13}}\} $和$\{ {\lambda _{21}}, {\lambda _{22}}, {\lambda _{23}}\} $分别是张量${D_1}$和${D_2}$的特征值；$\{ {\lambda '_{i1}}, {\lambda '_{i2}}, {\lambda '_{i3}}\} $表示${D_1}$和${D_2}$之间的第i个插值特征值集的对数；$i = 1, \cdots , k$，k表示插值个数；t表示与k有关的加权系数，$t = i/(k + 1)$.

扩散张量具有张量形状和取向两个特征.待插值张量的形状和大小可以由其三个特征值来表示，而方向是与欧拉角或单位四元数相关的.研究者采用分别对特征值和特征向量进行插值的方法，这样方便计算且能够保持较为理想的特性尤其是各向异性.对于张量的方向，研究者可以用欧拉角或四元数的方法进行插值.

1.3.2 基于欧拉角的插值

对于欧拉角方法，扩散张量D定义为

$\begin{array}{l} D = E\mathit{\Lambda} {E^{\rm{T}}} \\ E = \left( {\begin{array}{*{20}{c}} {{v_{11}}}&{{v_{21}}}&{{v_{31}}} \\ {{v_{12}}}&{{v_{22}}}&{{v_{32}}} \\ {{v_{13}}}&{{v_{23}}}&{{v_{33}}} \end{array}} \right) \\ \mathit{\Lambda} = \left( {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0 \\ 0&{{\lambda _2}}&0 \\ 0&0&{{\lambda _3}} \end{array}} \right) \\ \end{array} $

(14)

其中E是D张量的特征向量矩阵，Λ是张量D的特征值对角矩阵.

由于旋转矩阵不改变扩散张量的形状和尺寸，而只改变张量的取向，所以任意张量D'都可以从对角元素为D'的特征值的对角张量旋转得到，换句话说，旋转矩阵R等于特征向量矩阵E，即

$R = \left( {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\cos \alpha \cos \beta \sin \gamma - \sin \alpha \cos \gamma }&{\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma } \\ {\sin \alpha \cos \beta }&{\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma } \\ { - \sin \beta }&{\cos \beta \sin \gamma }&{\cos \beta \cos \gamma } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{v_{11}}}&{{v_{21}}}&{{v_{31}}} \\ {{v_{12}}}&{{v_{22}}}&{{v_{32}}} \\ {{v_{13}}}&{{v_{23}}}&{{v_{33}}} \end{array}} \right)$

(15)

因此，张量的欧拉角三元组^[20]为

$\left\{ \begin{array}{l} \alpha = a\tan 2({v_{12}}, {v_{11}}) \\ \beta = a\tan 2( - {v_{13}}, \sqrt {v_{11}^2 + v_{12}^2} ) \\ \gamma = a\tan 2({v_{23}}, {v_{33}}) \\ \end{array} \right.$

(16)

其中$a\tan 2(y, x)$是x，y的四象限反正切.

1.3.3 基于四元数的插值

对于单位四元数$q = {[w, x, y, z]^{\rm{T}}}$，对应的旋转矩阵R ^[21]如下：

$R = \left( {\begin{array}{*{20}{c}} {1 - 2{y^2} - 2{z^2}}&{2xy - 2wz}&{2xz + 2wy} \\ {2xy + 2wz}&{1 - 2{x^2} - 2{z^2}}&{2yz - 2wx} \\ {2xz - 2wy}&{2yz + 2wx}&{1 - 2{x^2} - 2{y^2}} \end{array}} \right)$

(17)

通过组合(14)、(15)和(17)式，可以使用以下等式获得对应于扩散张量D的单位四元数$[w, x, y, z]$：

$R = \left( {\begin{array}{*{20}{c}} {1 - 2{y^2} - 2{z^2}}&{2xy - 2wz}&{2xz + 2wy} \\ {2xy + 2wz}&{1 - 2{x^2} - 2{z^2}}&{2yz - 2wx} \\ {2xz - 2wy}&{2yz + 2wx}&{1 - 2{x^2} - 2{y^2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{v_{11}}}&{{v_{21}}}&{{v_{31}}} \\ {{v_{12}}}&{{v_{22}}}&{{v_{32}}} \\ {{v_{13}}}&{{v_{23}}}&{{v_{33}}} \end{array}} \right)$

(18)

从(18)式可以得到单位四元数$[w, x, y, z]$与特征向量之间的关系，如下：

$\left\{ \begin{array}{l} 4{w^2} = 1 + {v_{11}} + {v_{22}} + {v_{33}} \\ 4{x^2} = 1 + {v_{11}} - {v_{22}} - {v_{33}} \\ 4{y^2} = 1 - {v_{11}} + {v_{22}} - {v_{33}} \\ 4{z^2} = 1 - {v_{11}} - {v_{22}} + {v_{33}} \\ 4xy = {v_{21}} + {v_{12}} \\ 4xz = {v_{31}} + {v_{13}} \\ 4yz = {v_{23}} + {v_{32}} \\ 4wz = {v_{12}} - {v_{21}} \\ 4wy = {v_{31}} - {v_{13}} \\ 4wx = {v_{23}} - {v_{32}} \\ \end{array} \right.$

(19)

1.3.4 基于张量方向的插值

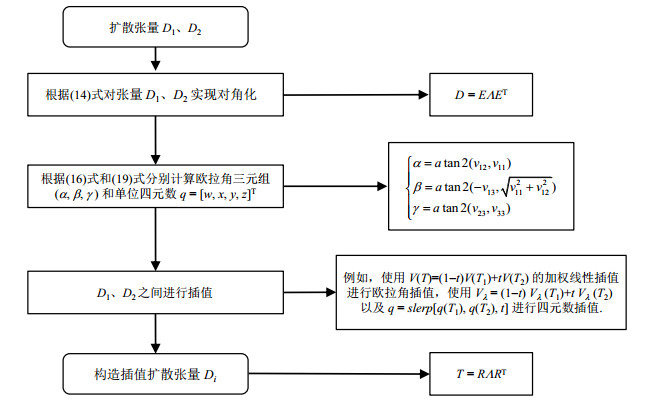
基于张量特征插值过程描述如图 2，其中$V = {[\ln {\lambda _1}, \ln {\lambda _2}, \ln {\lambda _3}, \alpha , \beta , \gamma ]^{\, {\rm{T}}}}$，${V_\lambda } = {[\ln {\lambda _1}, \ln {\lambda _2}, \ln {\lambda _3}]^{\, {\rm{T}}}}$.

最常用的四元数插值方法称为slerp^[38]，该方法的特点是得到球面内最短的测地线路径和较宽的角速度，根据给定张量${D_1}$和${D_2}$的单位四元数${q_1}$和${q_2}$，表示方向的插值四元数可以计算为：

$\left\{ \begin{array}{l} slerp({q_1}, {q_2}, t) = \frac{{{q_1}\sin [(1 - t)\theta ] + {q_2}\sin (t\theta )}}{{\sin \theta }} \\ \cos \theta = {q_1} \cdot {q_2} \\ \end{array} \right.$

(20)

虽然这些方法实现了保持部分张量性质不变的目标，但却忽略了保持张量的各向异性.为了解决这个问题，Collard等^[39]提出了谱四元数插值（Spectral Quaternion Interpolation，SQ）方法.该方法是基于四元数的基础，定义了希尔伯特各向异性（Hilbert Anisotropy，HA）参数，将线性四元数插值权重替换为HA权重因子：

$\left\{ \begin{array}{l} q(t) = \omega _1^*(t){q_1} + \omega _2^*(t){q_2} \\ \omega _1^*(t) = (1 - t)\frac{{\alpha (H{A_1}, H{A_t})}}{{\bar \alpha }} \\ \omega _2^*(t) = t\frac{{\alpha (H{A_t}, H{A_2})}}{{\bar \alpha }} \\ \alpha (H{A_1}, H{A_2}) = f[\min (H{A_1}, H{A_2})] \\ f(x) = \frac{{{{(\beta x)}^4}}}{{1 + {{(\beta x)}^4}}} \\ \end{array} \right.$

(21)

其中，β是设定的参数，$H{A_1}$和$H{A_2}$分别为张量${D_1}$和${D_2}$的希尔伯特各向异性，$HA = \ln ({\lambda _{\max }}/{\lambda _{\min }})$，$\bar \alpha = (1 - t)\alpha (H{A_1}, H{A_t}) + t\alpha (H{A_1}, H{A_2})$.该方法降低了计算难度，并允许一些理想的性质，包括特征值和体积的几何插值，希尔伯特各向异性的线性插值，以及各向异性较小时即方向是不确定时旋转的阴影等.SQ算法的具体步骤如下：

1）输入两个张量D₁、D₂，以及插值系数t；

2）根据(12)式进行两张量谱分解，特征值为递减阶；

3）根据(19)式计算表示方向的四元数，q₁和q₂以及相关的集合Q₂；

4）根据(13)式计算插值特征值矩阵Λ(t)；

5）根据(21)式计算插值四元数q(t)；

6）根据(18)式计算对应于q(t)的旋转矩阵R(t)；

7）根据D(t)=R(t)Λ(t)R(t)^T，计算插值张量D(t).

SQ方法能够保持插值张量各向异性的同时提高计算效率，但是该方法只对待插值张量的方向进行修正，却没有对张量的形状大小进行修正.因此，徐永红等^[40]在传统SQ的基础上提出了一种改进的谱四元数插值方法（Improved Spectral Quaternion Interpolation，ISQ）.该方法首先对扩散张量进行谱分解实现对角化，然后用四元数表示张量的方向.对于张量的形状大小，利用简化的部分各向异性作为权重进行修正；对于张量的方向，利用相对各向异性（Relative Anisotropy，RA）取代SQ方法定义的HA作为权重因子，最后加权平均得到待插值点的张量.其中，简化的部分各向异性及其权重因子定义为：

$ - \left[ \begin{array}{l} DA = \frac{{{{(\sum\limits_{i = 1}^3 {{\lambda _i}} )}^2}}}{{\sum\limits_{i = 1}^3 {\lambda _i^2} }} \\ \omega _1^* = (1 - t)\frac{{\gamma (D{A_1}, D{A_t})}}{{\bar \gamma }} \\ \omega _2^* = t\frac{{\gamma (D{A_1}, D{A_2})}}{{\bar \gamma }} \\ \gamma (D{A_1}, D{A_2}) = f[\min (D{A_1}, D{A_2})] \\ \bar \gamma = (1 - t)\gamma (D{A_1}, D{A_t}) + tr(D{A_t}, D{A_2}) \end{array} \right. $

(22)

其中DA、$D{A_1}$和$D{A_2}$分别为张量D、${D_1}$和${D_2}$的简化的部分各向异性，$D{A_t}$是指插值张量在t时刻简化的部分各向异性，此时，特征值的插值公式为：

$\mathit{\Lambda} (t) = \exp [\omega _1^*\ln ({\mathit{\Lambda} _1}) + \omega _2^*\ln ({\mathit{\Lambda} _2})]$

(23)

2 评估指标

目前用于评估张量插值方法优劣的指标主要有计算效率、不变性准则、质量特性以及定量标准.

2.1 计算效率

仿射不变黎曼几何插值是固有的，而log-E和SQ插值是非本征的，即插值曲线是嵌入在空间内的插值曲线在流形上的投影^[39].外在几何能够提高计算效率，因为它们减少了矩阵指数和矩阵对数的使用.通过把张量的几何形式转变为流形上的投影，可以节省Matlab代码，降低计算难度.

2.2 不变性准则

标量插值公式是按比例不变的，即

$\forall \lambda > 0, {\rm{ }}D(t;\lambda {D_1}, \lambda {D_2}) = \lambda D(t;{D_1}, {D_2})$

(24)

其中，$D(t;{D_1}, {D_2})$表示两张量${D_1}$和${D_2}$间t待插值点的张量，$\forall \lambda $是任意正数.

当处理提供物理强度的正测量时，这种不变性准则是可取的，因为它能够使过程对单元（或校准）具有鲁棒性^[39].同样，研究者可以根据矩阵插值公式是否是全等和按比例缩放不变的准则进行判别，即

$\forall \lambda \in {R^ + }, {\rm{ }}\forall U \in SO(3), {\rm{ }}D(t;\lambda U{D_1}{U^{\rm{T}}}, \lambda U{D_2}{U^{\rm{T}}}) = \lambda UD(t;{D_1}, {D_2}){U^{\rm{T}}}$

(25)

其中，$\forall \lambda $是任意正数，U表示齐次空间的任意矩阵，SO(3)表示行列式等于1的特殊正交旋转矩阵.

2.3 质量特性及定量标准

质量特性是指对张量性质的保持，主要包括正定性、扩散张量行列式的不变性、MD以及FA等.MD反映分子整体扩散水平和扩散阻力的整体情况，它包含了空间水分子扩散信息，只表示扩散的大小，与扩散的方向无关.FA定义为$\sqrt {\frac{{3[{{({\lambda _1} - \bar \lambda )}^2} + {{({\lambda _2} - \bar \lambda )}^2} + {{({\lambda _3} - \bar \lambda )}^2}]}}{{2(\lambda _1^2 + \lambda _2^2 + \lambda _3^2)}}} $，其中$\bar \lambda $，即MD值，是${\lambda _1}$、${\lambda _2}$、${\lambda _3}$的平均值.FA的取值范围是[0, 1]；0表示张量完全各向同性扩散，而1表示张量完全各向异性扩散.

为了观察张量形状的变化，Yang等^[41]还采用了第一特征值与第二特征值的比值，以及第一特征值与第三特征值的比值.当两个张量具有相同的比值时，说明它们具有相同的形状.此外，研究者还使用了定量标准，该标准涉及张量行列式以及FA或MD的均方误差，计算为

$MSE(X' - X) = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[X'(i, j) - X(i, j)]}^2}} } $

(26)

其中，$X'$表示插值图像的FA或MD值，X表示原始图像的值，M和N分别表示行数和列数.

3 实验

本文利用现有的典型张量插值方法——Log-E和SQ插值，对仿真数据以及真实的脑部胼胝体DTI数据进行插值实验并比较分析结果，从而全面系统地考察这两种插值方法的优劣.

3.1 仿真数据插值实验及结果分析

首先利用仿真数据分别进行两种方法的插值实验并比较分析实验结果.为了能够充分观察到待插值张量的变化情况，本文构造的仿真数据具有不同方向范围内相同形状的张量以及不同形状范围内相同方向的张量.首先根据自定义的张量旋转矩阵R以及不同的角度α来确定方向，然后通过选择不同的特征值来确定张量的大小.

第一步，对构造的两个仿真数据进行插值处理.这两个张量分别是${D_1}$和${D_2}$，旋转矩阵R为

$R = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }&0 \\ {\sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]$

(27)

其中，${\alpha _1} = \frac{{2{\rm{ \mathsf{ π} }}}}{{360}}$，${\alpha _2} = \frac{{2{\rm{ \mathsf{ π} }}}}{{360}} \times 63$，${D_1}$的特征值是[10,1,1], ${D_2}$的特征值是[40,4,1].

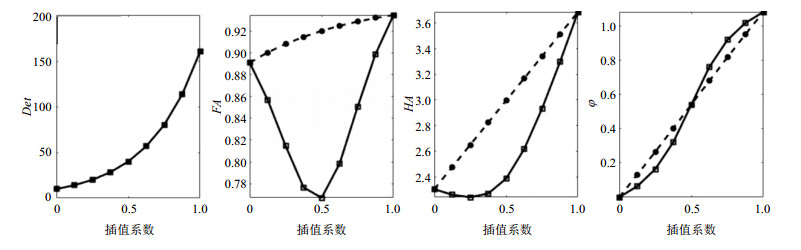
图 3是log-E与SQ方法在两个张量间的插值结果图.各向异性越高的张量，椭球的颜色越深.根据图 3椭球颜色以及形状的变化可以看出，log-E方法后半边的张量趋于各向同性，前后张量的变化太突兀，而SQ方法是渐变的插值过程，且张量的形状变化并不明显.图 4是两种方法的参数对比图，横轴表示插值系数，纵轴分别表示行列式（Det）、部分各向异性（FA）、希尔泊特各向异性（HA）以及主特征向量角度（$ \varphi $）.log-E和SQ两种插值方法的行列式曲线重合在一起，呈单调递增趋势，说明这两种方法的行列式变化是一致的，都能较好地抑制膨胀效应.但是对于FA以及HA的变化，只有SQ方法呈单调性，而log-E方法却出现最小值，表明log-E方法在某个张量插值处出现FA以及HA值的塌陷，此处张量的各向同性较大，抑制了各向异性.此外，只有SQ方法的主特征向量角度呈线性变化，因此SQ方法更能适应张量插值的各向异性保持.

第二步，对四个张量进行插值处理.这四个张量分别是${D_1}$、${D_2}$、${D_3}$和${D_4}$.其中，${D_1}$是3×3的单位矩阵，旋转矩阵仍是$R = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }&0 \\ {\sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]$，且${\alpha _2} = \frac{{\rm{ \mathsf{ π} }}}{4}$、${\alpha _3} = \frac{{\rm{ \mathsf{ π} }}}{2}$、${\alpha _4} = 0$.${D_2}$、${D_3}$和${D_4}$的特征值分别为[2, 0.2, 0.1]，[2, 1, 0.1]，[2, 1, 0.1].

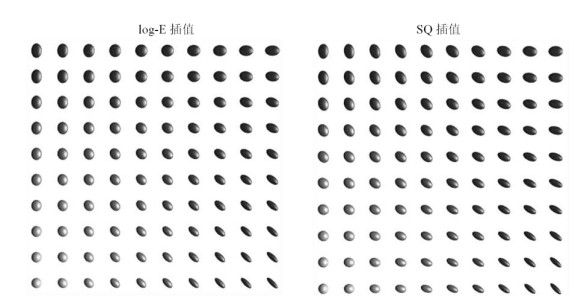
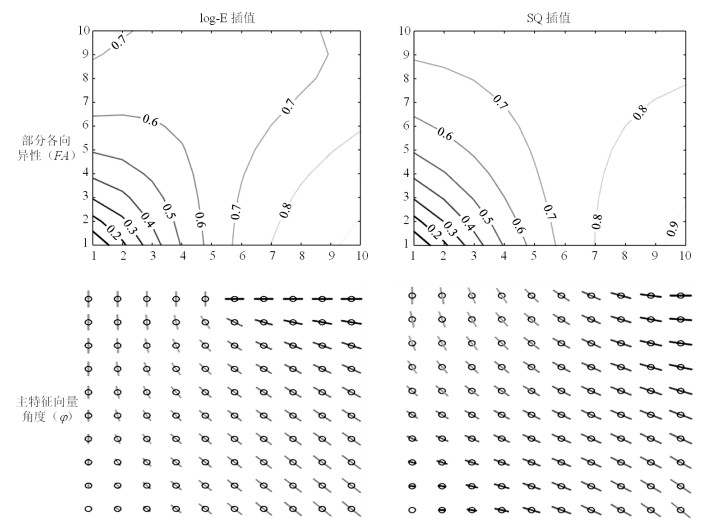
图 5是两种方法在四个张量间的插值结果.左侧为log-E插值，右端为SQ插值.对于四张量插值，插值权重由HA决定，所以张量的颜色与HA相关.图 6是两种方法的参数比较，第一行分别是log-E和SQ方法的FA等高线，第二行分别是log-E和SQ主特征向量角度.根据图 5所示的颜色变化，两个插值方法之间的差异明显可见.例如图 5第一行以及图 6的主特征向量夹角图第一行，它对应于具有相同形状但不同方向的两个正交张量之间的插值.采用log-E方法时，主特征向量直到插值的中点才变化，此处它被90°旋转，说明此处张量趋于各向同性.而SQ插值导致张量的单调旋转.由图 6所示的两种方法的插值张量FA等高线图可以看出，log-E方法的等值线间距越变越大，而SQ方法中等高线的间距更均匀，表明SQ方法比log-E方法更能使张量的各向异性恒定.

3.2 脑部胼胝体DTI插值实验及结果分析

如果仅根据仿真数据实验得出的结果，并不能系统地验证SQ插值方法的优点，所以我们还基于真实的张量脑部胼胝体DTI数据分别进行了两种方法的插值实验并比较分析结果.本文利用在华山医院采集的大小为128×128×60的脑部胼胝体DTI数据进行实验.为了能够清楚地观察到胼胝体的细节变化，本文选取该数据的第36层切片的部分数据，大小是40×40.首先对原始数据进行降采样，降采样后的数据大小变为20×20，张量椭球视图如图 7所示.

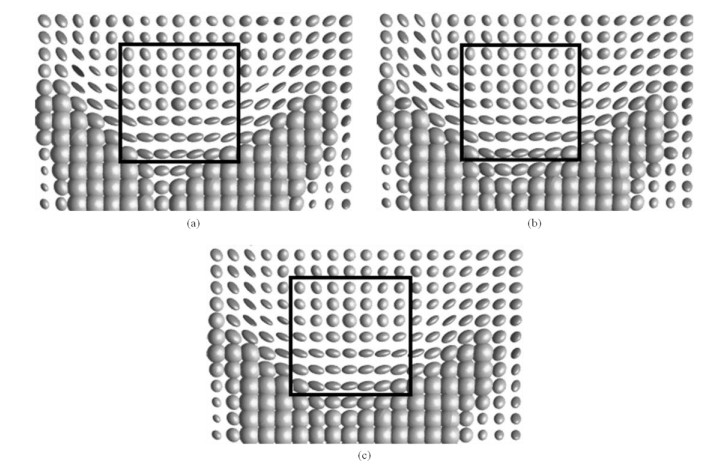
为了能够清楚地观察到胼胝体张量插值的细节变化，本文选取了图 7中黑色矩阵区域数据，其大小是4×4的张量分别进行对log-E以及SQ方法的插值实验，结果如图 8所示.

其中，从黑色矩阵区域内张量的椭球视图可以看出，与log-E方法的插值结果相比，SQ方法的实验结果具有较好的轮廓，有利于更清楚地分辨出细节，在保持图像的各向异性特征上具有优势.相对地，log-E插值使得图像的轮廓趋于平滑，方向性信息变化幅度较大.因此，根据仿真数据和真实数据的实验结果，本文证实SQ方法更具优越性.

4 结论

张量图像的插值处理是基于空间几何框架下，在给定的空间范围内，由已知采样点张量生成未知点张量的过程.它能够根据现有张量的信息来填补图像中未知点的信息.近年来，基于张量的分类神经性疾病^[42]的研究较为热门，如阿尔茨海默症，通过基于张量的独立成分分析去处理三阶灰度张量，有利于识别阿尔茨海默病和轻度认知障碍患者.同时，张量插值方法中加权均值的概念为图像处理提供了新的思路，如滤波、去噪、图像的变换、配准^[43]以及模板^[44-46]构建等方面，应用前景较为广阔.

目前，虽然存在不少关于扩散张量插值方法的研究，但是这些方法都是基于解决前人方法的某一个局限性展开的，并没有一项研究是较为系统地根据评估指标来提出插值方法.根据目前的张量插值方法的研究基础，未来的扩散张量插值研究需要考虑以下几个方面：

1）与基于欧几里德插值、RSS插值和log-E方法相比，基于特征插值框架中的欧拉角或四元数的插值为临床应用提供了改进的方法.同时，欧拉角或四元数为张量方向插值提供了灵活的选择.四元数虽然不需要选择坐标系，但在实践中很难实现更复杂的插值.此外，欧拉角和四元数会产生不同的张量方向插值路径，可能导致不同的纤维追踪结果，但是研究者并不能判别哪种方法是较适合的.因此，对于实践中更复杂的多维度插值是未来研究的突破点；

2）目前的张量插值是基于待插值点附近的四个张量进行插值，在特殊的高角度分辨率扩散张量图像（High Angular Resolution Diffusion Imaging，HARDI）应用中，需要处理更复杂的扩散张量模型；

3）不少插值研究中，对于插值权重因子的选择是与张量的特性如FA或者HA等相关的，目前为止并没有研究证明这种基于特性的特定插值权重适用于所有张量，所以未来应当根据不同的应用，选择不同的插值权重因子；

4）近年来，对于插值方法的评估指标方面仍缺乏“金标准”，与临床评估指标相关的张量特性并不存在视觉或者客观评价的标准.因此研究通用的评估指标对于张量的插值具有重要的临床意义.