天然产物在现代药物研发中有着举足轻重的地位,在已上市或在研药物中,有大量分子实体都来源于天然产物及其衍生物[1].在天然产物研究中,结构解析无疑是最重要的环节之一,它是后续研究(如活性评价、药理作用机制、有机合成和生物合成研究等)的重要基础.传统的天然产物结构解析往往依靠核磁共振(nuclear magnetic resonance,NMR)波谱、质谱(mass spectrometry,MS)、紫外光谱(ultraviolet‑visible spectroscopy,UV)、红外光谱(infrared spectroscopy,IR)、旋光光谱(optical rotatory dispersion,ORD)、电子圆二色谱(electronic circular dichroism,ECD),以及单晶X-射线衍射(single crystal X-ray diffraction,SXRD)等技术.其中,MS与各种光谱通常只能提供相对有限的信息;尽管SXRD是一种相对直接、客观的确定化合物平面结构及立体构型的方法,但适合于SXRD实验的晶体的获得往往又受制于样品量及样品物化性质等多方面因素;NMR谱图因可以提供化学位移(δ)、偶合常数(J)、同核/异核相关、质子空间相关等丰富信息而一直被作为天然产物结构解析中最常规、最重要的手段[2-6].然而,由于NMR图谱的解析很大程度上依赖于解析者对于谱图信息的理解,且NMR谱图仍存在一些内在的局限性,因而,尽管与NMR相关的硬件与方法学近年来迅速发展[7],但其用于复杂天然产物的结构解析,尤其是立体构型的确定依然颇具挑战[8],这从发表于各大主流化学期刊中层出不穷的错误结构及其纠错论文中也可见一斑[9-12].
21世纪初,Bifulco等[13, 14]开创性地将量子化学计算NMR参数(quantum chemical calculation of nuclear magnetic resonance parameters,qcc-NMR)引入天然产物的结构解析中.在过去的十多年中,随着量子化学理论与计算机硬件、软件的不断发展,qcc-NMR方法也日趋成熟,以较小的计算成本就可以获得较高的计算精度,同时,对于NMR参数计算结果的分析也从简单的统计学方法逐渐发展为基于更为复杂的统计学原理或人工神经网络的方法[15].这些进展都促使qcc-NMR在天然产物研究中得到了越来越广泛的应用,并成为传统NMR技术、MS和各种光谱技术的重要补充.对于qcc-NMR,已有较多经典综述[16-21]可供参考.但这些综述或内容相对陈旧,或撰写较为简略,或未偏向于在天然产物中的应用.本文将重点关注qcc-NMR,特别是δH、δC、JH-H、JC-H和JC-C的量子化学计算,在天然产物结构解析中的应用,并对近年来的一些应用实例进行较为详细的分析.此外,鉴于上述综述中已对qcc-NMR相关理论进行了较为详尽的阐述,本文将不再赘述.
1 qcc-NMR的作用通过量子化学计算分子中相关原子(一般为碳原子或氢原子)的NMR屏蔽常数(σ),经过一定的数据转换,即可以得到相关原子的化学位移.此外,利用量子化学方法还可以计算预测JH-H、JC-H和JC-C.将NMR参数计算值与实测值进行比较,可达到以下目的:
(1)确定分子构造(molecular constitution,或称平面结构),即分子中的原子组成与连接方式.只通过NMR图谱的解析,常常不能最终确定复杂的天然产物的结构,而是得到多个具有不同分子构造的备选结构.将各个可能的构造异构体(constitutional isomers)的NMR参数计算值分别与实测值进行比较后,可通过两者的吻合度来判断最可能的正确分子平面结构.如张勇慧团队[22]从甘蓝链格孢菌(Alternaria brassicicola)中分离得到了brassicicene C,并通过δC的量子化学计算纠正了它们的骨架结构(图 1).
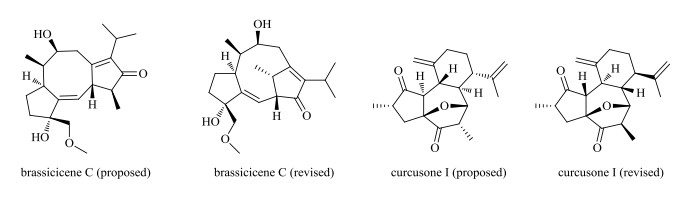
|
图 1 Brassicicene C[22]和curcusone I[23]的原定化学结构与纠正后的化学结构 Fig. 1 Originally proposed and revised chemical structures of brassicicene C[22] and curcusone I[23] |
(2)确定分子立体构型(molecular configuration).在天然产物结构解析中,更为常见的情景是,研究者通过解析NMR图谱,确定了分子构造,但未确定或仅确定了部分手性中心的立体构型.此时,可将该分子所有可能的非对映异构体(diastereoisomer)的NMR参数计算值分别与实测值进行比较,然后通过两者的吻合度来判断最可能的正确立体构型.如Sarotti等[23]应用NMR化学位移的量子化学计算,对从麻疯树(Jatropha curcas)中分离得到的二萜类化合物—curcusone I的立体构型进行了纠正(图 1).需要注意的是,由于对映体具有相同的NMR数据,因而通过qcc-NMR通常仅能确定分子的相对构型(relative configuration).然而,当分子中所有手性中心的相对构型均已确定,如有若干手性中心的绝对构型已知,此时亦可确定分子的绝对构型(absolute configuration).近期,Sarotti等将NMR化学位移的量子化学计算、DP4+可能性分析[24]与借助手性衍生化试剂(chiral derivatizing agents,CDA)确定绝对构型的方法(如改良的Mosher法)[25]进行结合,在确定衍生化底物的绝对构型方面取得了较好的成效[26].
(3)确证分子结构(structure validation).与上述两种基于对比的情景不同,天然产物结构解析中还常存在以下情景,即通过NMR图谱解析出一个分子结构时,需验证其结构的正确性.如本课题组从狭叶五味子(Schisandra lancifolia)中分离得到了lancolide E,通过波谱解析初步确定了其平面结构及相对构型,该结构进一步通过δC的量子化学计算得到验证,并经SXRD实验得到证实[27]. 须注意的是,当对不同分子进行量子化学计算,或对同一分子使用不同方法进行计算时,由于存在一定差异的计算误差,因而用于评价计算结果的一般性统计学参数并无明确的阈值可用以指示当前计算的分子结构的正确性.此时应更加慎重并尽可能结合其它证据以提高判断的准确度.
(4)辅助数据归属(NMR data assignment).尽管目前已有多种NMR图谱用于天然产物NMR数据的归属,但由于图谱中信号重叠、二维相关缺失或指示信息模糊等原因,在特定情况下,对分子中各原子的NMR信号进行准确归属仍具有一定难度,而通过qcc-NMR则可以更好地辅助数据归属.
2 qcc-NMR的基本流程Hoye等[28]对NMR化学位移的量子化学计算提供了一套“标准流程”,可供非专业人员参考.本节将基于最新研究进展,对qcc-NMR的流程进行更为详细的说明.目前可以进行qcc-NMR的程序较多,其中以Gaussian[29]应用最为广泛,此外,ORCA(免费程序)[30]、Dalton(免费程序)[31]等程序也具备相应功能.具体计算流程如下文所述.
2.1 确定初始结构在进行计算之前,首先需要明确计算对象.用以计算的初始结构必须是分子构造及相对构型明确的分子,这一结构往往通过NMR谱图、MS谱图和各种光谱分析,或SXRD实验获得.对于通过以上手段尚不能确定完整平面结构或立体构型的分子,可将所有可能的构造异构体或非对映异构体分别作为独立的计算对象进行计算.
2.2 构象搜索(conformational searching)天然产物的构象异构体(conformational isomers)是因分子中单键旋转而形成的立体异构体.单键旋转的能垒通常很低,相对于NMR时标(NMR time scale)而言,构象间的转换速度往往更快,因此室温下采集得到的NMR谱图为时间平均谱(time-averaged spectra).对于一个在溶剂中存在多种构象的分子,我们首先需要对每一个构象的NMR参数进行计算,然后根据各构象的玻尔兹曼分布(Boltzmann distribution)对计算数据进行加权,即可得到该分子各种NMR参数的计算值.
构象搜索的方法主要包括随机搜索法(stochastic methods)和系统搜索法(systematic methods)两类.其中,随机搜索法一般包括基于分子动力学(molecular dynamics,MD)、蒙特卡罗模拟退火(Monte Carlo-simulated annealing,MC)、距离几何(distance geometry,DG)和遗传学算法(genetic algorithms,GA)的方法等.而系统搜索法则主要包括暴力系统搜索法(brute force systematic conformational searching)与基于规则的系统搜索法(rule-based conformational searching)等[32].目前,在天然产物量子化学计算研究中常用的商业构象搜索软件主要包括Macromodel(Schr dinger,LLC,New York)、Spartan(Wavenfunction,Irvine)、Conflex(CONFLEX Corporation,Tokyo),以及GaussView6(Semichem Inc.,Shawnee Mission)中的GMMX模块等,而免费软件则包括Balloon[33]、Frog2[34]、Amber[35]、Gromacs[36]和GFN-xTB[37]等等.一般而言,在构象采样(conformation sampling)过程中或采样完毕后,程序(或操作者应用其它程序)会对获得的构象集(conformer ensemble)以基于分子力场(如MMFF94[38]、OPLS2005[39]力场等)或半经验方法(如PM6[40]、GFN-xTB等)计算获得的能量进行打分和排序,以便操作者选取特定能量窗口(energy window,即相对能量的阈值,如5 kcal/mol)内的构象进入下一步操作.为避免丢失重要构象,也可增大能量窗口或在能量窗口以外区域进行随机取样.对于构象较多的情况,可先以半经验方法在MOPAC(Stewart Computational Chemistry,Colorado Springs)或Gaussian[29]等程序中对构象进行优化,以构象间的几何偏差,如均方根偏差(root-mean-square deviation,RMSD)、距离矩阵(distance matrix)偏差等,及能量差为标准去除重复构象,并再次取特定能量窗口内的构象进入下一步操作.以上操作可保证进入下一步操作的构象不仅质量较高,且数量可以接受.
2.3 构象优化与振动分析密度泛函理论(density functional theory,DFT)是进行天然产物分子构象集几何优化(geometry optimization)及振动分析(frequency analysis)最常用的方法.在泛函选择方面,B3LYP[41]是使用最为广泛的泛函;在计算资源允许的情况下,M06-2X[42]、ωB97X-D[43]等泛函也是较好的选择,它们往往可以给出更为可靠的计算结果;对于B3LYP、M06-2X等泛函,也可通过增加色散矫正(dispersion correction,如DFT-D3[44])进一步改善计算结果.在基组选择方面,Pople系列基组较为常用,一般至少使用2-ζ基组(6-31G[45]);考虑计算需要及计算成本,可适当提升为3-ζ基组(6-311G[46])或更高基组,并适当添加极化函数和弥散函数;除Pople系列基组外,Ahlrichs系列基组(如def2-SVP、TZVP、def2-TZVP等)[47, 48]也较为流行.Tantillo等[18]认为qcc-NMR几何优化理论水平(level of theory)的底线是B3LYP/6-31G(d).
振动分析和几何优化必须在相同的理论水平下进行,否则分析结果将毫无意义.此外,因两者耗时较长,且分析结果对基组的敏感性相对较低,因而在进行几何优化和振动分析时,一般仅选用中小基组.必要时可对构象进行多步几何优化.如先在较低的理论水平下对构象进行优化(如气态下),然后取一定能量阈值内的构象在较高的理论水平下再次进行几何优化及振动分析(并考虑溶剂效应).通过振动分析并检查优化所得构象无虚频(imaginary frequency)后,即可确认该构象为势能面(potential surface)上真实的极小点.通过振动分析也可以获取后续计算需要的一些热力学数据,如吉布斯自由能的热校正能(thermal correction to Gibbs free energy),该能量与电子能量(electronic energy)之和即为构象的吉布斯自由能.由于电子能量的计算对于计算理论水平的敏感性相对较高,因而可对以上构象使用相对于几何优化更高的理论水平进行单点能计算(single-point energy calculations),以获得更为准确的电子能量,进而得到更为准确的吉布斯自由能.如对于构象i,
| $\mathit{\Delta} G_i^{lt2} = E_i^{lt2} + (G_i^{lt1} - E_i^{lt1})$ | (1) |
在几何优化完成并获得构象的吉布斯自由能之后,可以构象间的几何偏差及能量差为标准去除重复构象;进而利用去重复后各构象的吉布斯自由能,根据玻尔兹曼分布率计算各构象的玻尔兹曼分布:
| ${p_i} = \frac{{{n_i}}}{{\sum\nolimits_j {{n_j}} }} = \frac{{{{\rm{e}}^{ - \mathit{\Delta} {G_i}/RT}}}}{{\sum\nolimits_j {{{\rm{e}}^{ - \mathit{\Delta} {G_j}/RT}}} }}$ | (2) |
其中
由此,便获得了一组玻尔兹曼分布明确的分子构象,此时可取玻尔兹曼分布在特定阈值(如1%或5%)以上的构象进行下一步计算,但在此之前,通常应进一步借助实验测得的偶合常数及核Overhauser效应(nuclear Overhauser effect,NOE)相关数据来检验优化所得构象与NMR实验数据的一致性.然而,对于柔性分子或复杂分子,这一操作往往难以进行.基于这一背景,Butts等[49-51]提出对于一致性较差的情况,应对优化过程和构象搜索过程进行检查,必要时应进行重新优化或重新搜索,以免出现丢失个别或一类重要构象的情况.
2.4 δC和δH的量子化学计算方法天然产物NMR化学位移的量子化学计算最常用的理论方法为DFT.其中,在计算NMR屏蔽常数时存在“gauge难题”[52],而gauge不变原子轨道(gauge invariant atomic orbitals,GIAO)[53]与gauge转换的连续集(continuous set of gauge transformations,CSGT)[54]方法是目前最常用的解决该难题的方法.特别是GIAO,是Gaussian程序中计算NMR参数的默认方法,也是天然产物量子化学计算时的首选方法.
对于天然产物NMR化学位移量子化学计算时泛函与基组的选择,因现有的标杆性分析(benchmarking)[55, 56]往往以结构简单、分子量较小的分子作为测试集,且通常使用高精度方法的计算结果作为参考值,因而分析结果对于天然产物NMR化学位移计算的指导意义相对有限.WC04和WP04泛函[57]是Cramer专为在氯仿溶液中δC和δH量子化学计算所优化的泛函,如Hoye等[58]通过对phomopsichalasin进行详尽的NMR波谱数据分析,并对比其简化结构在WP04-SCRF/pcS-2//M06-2X/6-31+G(d, p)理论水平及甲醇溶剂(pcm溶剂模型)中δH计算值,最终对其结构进行了纠正.KT2[59]也是专为NMR参数计算而优化的泛函,但目前仅被Dalton程序支持.天然产物qcc-NMR常用的泛函包括mPW1PW91[60]、B3LYP、B97-2[61]和PBE0[62]等;常用基组包括Pople系列和Ahlrichs系列基组,以及专为NMR化学位移计算构建的pcS-n系列基组[63]及其片段收缩版本,即pcSseg-n系列基组[64].需注意的是,pcS(或pcSseg)-n系列基组非Gaussian程序内置基组,使用时需要在Basis Set Exchange网站(https://www.basissetexchange.org/)拷贝定义.关于NMR化学位移的量子化学计算方法,文献[28, 56, 65-69]与CHESHIRE数据库中均有推荐,部分方法可见表 1.需要注意的是,对于NMR化学位移的量子化学计算,不应盲目使用较高的理论水平:其一方面会导致耗时暴增;另一方面,计算理论水平的提高不一定能提升计算结果的准确性[56].
| 表 1 部分文献与CHESHIRE数据库中推荐的NMR化学位移的量子化学计算方法 Table 1 Classical methods recommended in literatures and CHESHIRE database for quantum chemical calculation of NMR chemical shift |
NMR化学位移量子化学计算时输出各个构象分子的每个原子的屏蔽常数后,可根据构象玻尔兹曼分布通过数据加权得到该分子各原子的屏蔽常数,然后通过以下方法将其转化为各原子的化学位移:
(1)使用参考物质(reference).最常用的方法是在相同理论水平下计算参考物质,如四甲基硅烷(tetramethylsilane,TMS)的屏蔽常数,再以公式(δi =σref –σi +δref)计算即可得到每个原子的化学位移(其中δi为第i个原子的计算化学位移,σref为参考物质的计算屏蔽常数,σi为第i个原子的计算屏蔽常数,而δref为参考物质的实测化学位移).
Sarotti等[70, 71]发现,当使用多参考标准方法(multi-reference standard approach,MSTD)时,计算结果相对于仅使用TMS作为参考物时准确性显著提高,且计算结果准确性对于计算理论水平的依赖性明显降低.具体方法为,对sp3杂化碳原子及与其连接的氢原子使用甲醇作为参考物质,而对于sp或sp2杂化碳原子及与其连接的氢原子使用苯作为参考物质.
对于以上方法计算得到的各原子的化学位移可进一步通过与对应的实验数据进行线性回归分析(linear regression analysis)及数据校正(correction或scaling)来消除计算的系统误差.
(2)标度法(scaling method)[18].标度法的基本原理是,选取一批有机小分子作为测试集,在特定的理论水平下对测试集中的所有分子进行优化及屏蔽常数计算,即得到所有分子中所有的σC或σH,将其与对应的δC或δH实测值进行线性回归分析,即可以得到对应的线性回归方程:σ=aδ+b(其中σ代表计算屏蔽常数,δ代表实测化学位移,a为回归曲线的斜率,而b为回归曲线的截距).在获得该线性回归方程后,即可以在相同方法下对其它分子进行计算,并将计算得到的σC或σH代入公式δi = (σi – b)/a,就可以得到该分子的计算化学位移(其中δi为第i个原子的计算化学位移,σi为分子中第i个原子的计算屏蔽常数,a和b分别为以上回归曲线的斜率和截距).CHESHIRE数据库(http://cheshirenmr.info/)提供了在不同几何优化及化学位移计算理论水平下得到的标度参数(a和b),可供研究者直接使用.研究者也可利用数据库中提供的训练集分子坐标及相关脚本,在自己感兴趣的理论水平下拟合标度参数.鉴于天然产物丰富的结构多样性,在对特定类型的分子进行研究时,也可选取一批结构确定的该类型分子作为训练集来拟合标度参数.
(3)经验校正方法(empirical correction).经验校正方法的基本原理与标度法类似,即在特定的理论水平下对测试集中的所有分子进行优化及化学位移计算,然后根据计算结果获取校正数值或参数,将其用于其它分子的计算.如Gonnella等[66]对一系列分子进行计算并通过使用TMS作为参考物质得到δC,其中处于特定化学环境(如连接卤原子、磺酰基)的δC计算值具有明显的系统误差,通过数据分析,提出了对这些δC计算值进行数值校正的方法,该校正数值来源于训练集中相关核计算误差的平均值.而对于被卤原子取代的碳原子,常规计算方法往往难以获得准确的计算结果,Kutateladze等[67, 68]在计算得到相关核的屏蔽常数后,基于统计学方法提出了二次方程校正的方法(σcorr = aσ2+ bσ + c,其中σcorr与σ分别为相关核校正后与校正前的屏蔽常数,a、b和c均为校正参数),在获得相关核的σcorr后,再利用标度法将所有核的σcorr计算值转化为化学位移计算值.这一方法也可应用到普通化学环境下δC和δH的计算中.
2.5 JH-H、JC-H和JC-C的量子化学计算方法两个自旋不为0的原子核,在距离相近时,由于核磁矩之间的自旋-自旋偶合(spin-spin couplings)作用,会造成NMR谱峰的裂分,自旋-自旋偶合作用的强度以自旋-自旋偶合常数表示,其与费米接触项(fermi contact,FC)、自旋偶合(spin dipolar,SD)、顺磁自旋轨道(paramagnetic spin-orbit,PSO)及抗磁自旋轨道(diamagnetic spin-orbit,DSO)四种机制相关,其中FC项对于偶合常数的贡献最大,这已是共识[72].偶合常数对于有机分子的构象及构型研究至关重要,如基于偶合常数的构型分析(J-based configurational analysis,JBCA)方法[16, 73],即利用3JH-H、3JH-C及2JH-C等信息来确定碳链上相邻或间隔一个原子的两个手性中心的立体构型.但由于这些方法的核心都是利用一些经验性参数,因而往往只适用于特定的情景.如Karplus方程:3JH-H (ϕ) = A cos2 ϕ + B cos ϕ + C,常被用以将3JH-H与相邻两根X-H键的二面角进行关联,但经验参数A、B和C的值与氢原子所连接的原子,以及原子上的取代基性质、相关键角等诸多化学环境因素有关.而量子化学计算不对化学环境做任何假设,因而可以准确预测有机分子中的偶合常数.
Rablen等[72]应用一个从65个分子中提取出的165个覆盖广阔“化学空间”的JH-H作为训练集,评价了250种偶合常数计算方法.他们发现,在B3LYP/6-31G(d, p)理论水平下,通过非收缩基组并对内核添加紧凑的极化函数,仅计算FC项,并对计算结果乘以校正因子(0.911 7),即能在较小计算成本下获得计算精度较高的JH-H计算值.
Kutateladze等[74, 75]开发的“相对力场(relativistic force field,rff)”方法则在精确计算FC项的基础上,通过结合经验校正参数及NBO杂化系数,将FC项参数化,以此来补充校正其它项(SD、PSO、DSO)的贡献,并由此开发出了两个基组,即DU8和DU8C,皆能以较小计算成本进行计算,分别得到较为精确的JH-H与JC-H计算值.
Bifulco等[76]对模型分子士的宁(strychnine)及其12种立体异构体的1JC-C进行了计算,计算在B3LYP/6-311+G(d, p)理论水平下进行,并在计算FC项时对内核添加紧凑的极化函数.结果显示,士的宁的1JC-C计算结果良好,且在13种立体异构体中最优.尽管目前JC-C在天然产物结构解析中应用并不广泛,但随着JC-C测量方法的灵敏度与准确性不断提高,必将有较大的应用潜力.
除以上方法外,pcJ-n系列基组[77]是专门为计算偶合常数而优化的基组(非Gaussian程序内置基组,使用时需要在Basis Set Exchange网站拷贝定义),带有很紧凑的高斯函数,也常常被用于天然产物偶合常数的量子化学计算.
2.6 NMR参数计算结果的分析与评价NMR参数计算完成后,需要将计算数据与对应的实验数据进行关联和分析.通常,当NMR图谱对应于多个可能的备选结构时,正确结构的计算数据与实验数据的吻合度理论上应高于其它备选结构.传统的评价方法是应用一些简单的统计学参数,如相关系数(correlation coefficient,R2)、平均绝对偏差(mean absolute errors,MAE)、校正后的平均绝对偏差(corrected mean absolute errors,CMAE)和RMSD等[28].当某备选结构的R2越接近于1,而MAE、CMAE及RMSD越小时,其越可能为正确结构.但实际上,各备选结构的计算数据通常非常接近,得到的关联参数差异较小或趋势不一致,导致无法明确指认正确结构.针对这个问题,近年来出现了一系列更为精确的计算结果分析方法,它们基于更为复杂的统计学或人工神经网络(artificial neural networks)原理,所提供的结论往往具有更高的可信度[15].在这些分析方法中,CP3[78]、DP4可能性分析[79](及其改良版DP4+[24]与DiCE[80],以及升级版DP4.2[81, 82]),以及ANN-PRA分析(artificial neural networks-pattern recognition analysis)[83, 84]是最为重要的三种分析方法.三种分析方法分别对应于三种不同的情景:(1)当存在两组NMR实验数据(A和B),对应于两个结构(a和b),但对应关系(A=a,B=b或者A=b,B=a)未知时,CP3方法可以辅助进行指认;(2)当存在一组NMR实验数据(A),但具有多个可能的备选结构时(A1~An),DP4可能性分析可以辅助确定正确的结构(A=An);(3)当通过一组NMR实验数据解析出一个结构时,ANN-PRA可辅助判断其正确性.以下将简要介绍三种方法的原理及使用方法.
2.6.1 CP3方法Goodman等[78]定义了CP1~CP3参数:
| $ {\rm{CP}}n = \frac{{\sum\nolimits_i {f(n)} }}{{\sum\nolimits_i {({\mathit{\Delta} _{{\rm{exptl}}}}} {)^2}}}-\left[ \begin{array}{l} {n = 1;{\rm{ }}f(1) = {\mathit{\Delta} _{{\rm{exptl}}}}{\mathit{\Delta} _{{\rm{calcd}}}}{\rm{ }}} \\ {{\rm{ }}n = 2;{\rm{ }}f(2) = \left\{ \begin{gathered} \mathit{\Delta} _{{\rm{exptl}}}^{\rm{3}}/{\mathit{\Delta} _{{\rm{calcd}}}}, \, {\rm{ }}|{\mathit{\Delta} _{{\rm{calcd}}}}|\, > \, |{\mathit{\Delta} _{{\rm{exptl}}}}| \\ {\mathit{\Delta} _{{\rm{exptl}}}}{\mathit{\Delta} _{{\rm{calcd}}}}, \, {\rm{ }}|{\mathit{\Delta} _{{\rm{calcd}}}}|\, \leqslant \, |{\mathit{\Delta} _{{\rm{exptl}}}}| \\ \end{gathered} \right.} \\ {n = 3;{\rm{ }}f(3) = \left\{ \begin{gathered} \mathit{\Delta} _{{\rm{exptl}}}^{\rm{3}}/{\mathit{\Delta} _{{\rm{calcd}}}}, {\rm{ }}{\mathit{\Delta} _{{\rm{calcd}}}}\, > {\mathit{\Delta} _{{\rm{exptl}}}} \\ {\mathit{\Delta} _{{\rm{exptl}}}}{\mathit{\Delta} _{{\rm{calcd}}}}, \, {\rm{ }}{\mathit{\Delta} _{{\rm{calcd}}}}\, \leqslant {\mathit{\Delta} _{{\rm{exptl}}}} \\ \end{gathered} \right.} \end{array} \right. $ | (3) |
其中
CP1~CP3可用以将两个结构(a和b)分别归属于两组NMR实验数据(A和B).相比MAE、CMAE及R2,CP1~CP3参数可以以更高的可信度做出正确的归属.此外,CP3为服从正态分布的独立随机变量,因而,对于一种特定的归属,即已知CP3参数的情况下,可根据贝叶斯定理(Bayes' theorem)求得该归属为正确的可能性.如Lee等[85]通过NMR化学位移计算并结合CP3分析,对一对齐墩果烷型三萜的C-3位差向异构体与其NMR实验数据进行了对应归属.
2.6.2 DP4、DP4+、DP4.2与DiCE方法Goodman等[79]对117个有机小分子在B3LYP/6-31G(d, p)//MMFF理论水平下进行NMR化学位移计算,并提取了其中1 717个δC及1 794个δH进行分析.结果发现,经线性校正后的计算数据与对应实验数据之间的计算误差(两者的差值)为独立的随机变量,且服从t分布.因而,对于一个分子中任意原子的计算误差,可借助以上分布通过求解累积分布函数(cumulative distribution function,CDF)及一定的数据换算,获得该误差所对应的可能性(probability),将所有原子计算误差对应的可能性相乘,即得到整个分子的可能性.在分别求解出所有备选结构的可能性后,通过贝叶斯定理就可以获得各备选结构为正确结构的可能性.
Sarotti等对DP4可能性分析方法提出了一定的质疑:首先,DP4方法中计算所使用的理论水平过低(如使用分子力场优化得到的构象进行NMR化学位移计算),导致计算结果的精度不够;其次,DP4方法使用了经线性校正的计算数据,这样的做法可能会增加假阳性的风险,即可能使错误结构的计算数据碰巧与实验数据更为吻合.Sarotti等发现,对于未经线性校正的计算数据,整个计算误差集并不服从t分布,但sp2原子与sp3原子的计算误差分别服从独立的t分布.因此作者通过(a)将两种不同杂化方式的原子分开考虑;(b)在不同理论水平下进行NMR化学位移计算并获取相应的计算误差分布参数(期望值、标准差、自由度);(c)同时考虑未经校正的计算结果与校正后的计算结果等手段,对DP4可能性分析方法进行了改良,并称之为DP4+[24].随后,Sarotti等[86]以一批含有螺原子或季碳的环氧化物为研究对象,证实了DP4+相对于DP4方法的优势.而Gonnella等[80]也基于DP4方法开发了DiCE方法,该方法的主要改进包括:(1)NMR化学位移计算采用了他们此前所建立的方法[66, 87];(2)用以DiCE分析的化学位移计算值经标度法得到;(3)在DiCE可能性分析中引入了δN的计算值与实验值.Gonnella等还对DP4、DP4+及DiCE三种方法进行了比较,并通过案例分析表明了DiCE与DP4+的表现明显优于DP4.Iron[56]对DP4方法中的统计学方法提出了一定的质疑,并做出了相应的修改.近期,Goodman团队[81, 82]对DP4分析方法的统计学模型进行了优化,使其整体表现显著提升,他们将这一升级版本称为DP4.2.
在DP4相关分析方法的应用中,需要注意以下几点:(1)使用DP4相关分析方法时,备选结构中必须包含正确结构;(2)可能性分析可基于13C核或1H核的数据,或基于两项数据,但同时应用两项数据时,往往能使结论的准确性更高;(3)在使用DP4相关分析方法时,应保证计算所使用的理论级别与相应方法提出时所使用的理论级别保持一致.
值得一提的是,近期,Sarotti等[26]将NMR化学位移计算、DP4+分析与CDA衍生法进行结合,以期将其用以确定分子的绝对构型.其基本原理为,以一种构型确定的CDA对绝对构型未知的底物(Sub)进行衍生化时,产物存在两种可能性,即Sub CDA与ent-Sub CDA,对这两种立体异构体进行NMR化学位移计算,并通过DP4+分析将NMR化学位移的计算值与实测值进行关联,即可确定底物的绝对构型.该研究采用了114个类型涵盖伯醇、仲醇、叔醇、伯胺的分子作为测试集,结果显示,当对底物进行单衍生化时(仅使用一种构型的CDA),可以正确确定大多数底物(96%)的绝对构型;当对底物进行双衍生化时,即可以进行两次独立的DP4+分析,借由两次的分析结果,Sarotti等引入了DIP(DP4+-integrated probability)分析方法,并使用该方法正确确定了所有受试案例(54个分子)的构型.总体而言,以上方法较好地弥补了传统CDA衍生化方法的一些缺陷,如未使用准确的构象模型进行屏蔽/去屏蔽作用分析,及可能出现Δδ值较小或符号不一致的情况.
2.6.3 ANN-PRA方法Sarotti等[83]将NMR化学位移计算与人工神经网络进行结合,开发出可以通过NMR计算判断所解析结构是否正确的方法.这一方法最初仅基于对13C核数据的模式识别(pattern recognition),但作者发现,其在结构错误较为细微时(如立体构型),常常不能给出正确的结论.因而,Sarotti等[84]在原先的神经网络中进一步整合了HSQC数据,使之在区分正确与错误结构的能力上,尤其在立体构型的判断方面得到了进一步提升.
3 qcc-NMR在天然产物结构鉴定中的应用实例 3.1 有机合成与qcc-NMR的结合用于Baulamycins的结构纠正抑制金黄色葡萄球菌与炭疽杆菌中嗜铁素的生物合成对于治疗由耐甲氧西林金黄色葡萄球菌或炭疽杆菌感染引起的疾病具有重大意义,基于这一背景,Sherman等[88]从大量海洋微生物的提取物中筛选可以特异性抑制嗜铁素合成酶的化合物,并最终从Streptomyces tempisquensis的提取物中分离得到两个具有显著活性的化合物,即Baulamycins A和B(图 2,以下分别简称BmcA和BmcB),有望成为抗生素研究的先导化合物.为给后续生物研究提供充足的样品,Goswami团队[89]与Aggarwal团队[90]均对BmcA进行了全合成,结果显示Shermen等提出的结构并不正确,Goswami团队合成了BmcA的两个立体异构体,然而其NMR图谱与原始图谱[88]仍不一致.BmcA和BmcB均具有柔性链状结构,原文中作者主要使用了JBCA方法[16, 73]对其构型进行确定.但由于BmcA和BmcB均具有多达7个手性中心,通过合成所有立体异构体(128种)来确定正确结构的做法显然难以实现,在意识到这一点后,Aggarwal团队决定以精确的qcc-NMR结合全合成方法对BmcA和BmcB的结构进行纠正.首先,因结构中的两个手性中心簇(stereoclusters)通过C-9、C-10两个亚甲基连接,因而该团队通过切断C-9/C-10将化合物分为两个片段(Fragments A和B)考虑.对于Fragment A,该团队首先通过与合成产物进行NMR数据对比将C1′-C14相对构型纠正为anti,进而只需要对4种可能的非对映异构体结构进行计算(计算时Fragment B使用原定结构).将各结构NMR参数(JH-H、δH、δC)的计算值与实验值通过MAE分析和DP4分析进行关联后,确定了其中一个立体异构体(Fragment A1,anti-anti-syn)与实验值吻合度最高.而对于Fragment B的4种可能的非对映异构体结构的计算则显示,存在两个立体异构体与实验数据较为吻合,且进一步通过合成确定了Fragment B的相对构型(Fragment B1,syn-syn).至此,两个片段的相对构型皆已确定,作者进一步通过合成确定了BmcA的正确结构及绝对构型,原定结构中的5个手性中心的绝对构型得到纠正(图 2).众所周知,对于柔性分子,准确计算NMR参数的难度极大,原因在于柔性分子中多具有大量可旋转键(如BmcA中即有多达14根可旋转键),导致分子构象众多(如对于BmcA的原定结构,构象搜索程序可搜索得到1 674个不同构象,即使以10 kJ/mol作为能量窗口,仍有98个构象).此外,由于在有限基组下很难获得各构象的准确能量,导致无法求得较为准确的玻尔兹曼分布,从而使NMR参数计算值的准确性大为降低.而上述研究中的计算之所以能获得较高精度,主要得益于以下几个因素:(1)采用了精度更高的能量计算方法进行构象筛选,主要体现为在较低理论水平进行构象优化,在较高理论水平进行能量计算,并考虑溶剂效应;(2)在完成构象搜索之后,对能量窗口之外的构象进行了随机取样,以免丢失重要构象;(3)Butts等[49-51]发现应用NOE方法能较为准确的测得分子中的质子间距离,Aggarwal团队基于此研究,对构象能量(即玻尔兹曼分布)进行了基于NOE距离的校正(NOE-distance based population refinement),即利用GRG非线性方差优化(GRG non-linear least squares optimization)的方法,使几何优化所得构象集的玻尔兹曼平均质子间距离(ensemble-averaged distances)与实测NOE距离具有最小的标准偏差,这一方法较好的弥补了DFT能量计算的不足,且使校正后的构象集与实际的构象集理论上更为“吻合”.

|
图 2 Baulamycins A和B的原定结构[88]与纠正后[90]的化学结构 Fig. 2 Originally proposed[88] and revised[90] structures of baulamycins A and B |
以上研究工作表明,有机合成与qcc-NMR方法的结合能将问题大为简化,此外,该研究[90]中所呈现的“精确的qcc-NMR方法”用于对细节的处理表现地淋漓尽致,值得其它研究者借鉴使用.
3.2 NMR化学位移量子化学计算结合DP4+可能性分析用于研究pseudo-rubriflordilactone B结构本课题组[91]于2006年报道了从红花五味子(Schisandra rubriflora)中分离得到的两个具有一定抗HIV-1病毒活性的五味子降三萜(schinortriteprnoids,SNTs)——rubriflordilactones A和B(以下简称Rub-A和Rub-B),两者都具有18-norschiartane型SNT骨架及芳构化D环,且结构得到SXRD实验证实.Rub-A和Rub-B复杂的化学结构吸引了有机合成化学家的注意,李昂团队[92]于2016年发表了Rub-B(图 3)的全合成工作,合成产物的结构也得到了SXRD实验证实.然而,合成Rub-B与天然产物的NMR数据明显不一致.李昂团队推测,在此前的植物化学研究中,由于Rub-B样品的不稳定性,导致其中少量样品发生了立体构型异构化,且由于异构化产物溶解度较低,从而形成了晶体并被检测得到SXRD数据[91],而样品中的大量成分(pseudo-Rub-B,以下简称PRub-B)(图 3)则被检测得到所报道的NMR数据[91].本课题组对采自相同产地的红花五味子进行了再次分离,但并未分离得到Rub-B或PRub-B.截止目前,仍没有公开发表的研究阐明PRub-B的结构.对于这一“Rub-B难题”,Sarotti等[93]希望尝试结合qcc-NMR与DP4+可能性分析来进行探索.PRub-B具有8个手性中心,因而理论上应具有128种可能的非对映异构体.为了缩小初步计算的范围,Sarotti等首先对其NMR图谱进行了分析,发现其结构左侧的NMR数据与具有相同结构片段的同类化合物基本一致,结合SNTs左侧构型常常比较保守这一背景,可以推断PRub-B结构左侧的3个手性中心(C-1、C-5和C-10)应与其它SNTs一致.因而将计算范围缩小到32种非对映异构体(原文[93]中编号分别为PRB33~64).该文作者首先将Rub-B的实测NMR化学位移[92]与32种非对映异构体的计算NMR化学位移通过DP4+可能性分析进行关联,发现Rub-B的正确结构(PRB48)具有高达92.6%的DP4+可能性,从而有力地验证了DP4+可能性分析方法的可靠性.进而,该文作者将PRub-B的实测NMR化学位移[91]与32种非对映异构体的计算NMR化学位移通过DP4+可能性分析进行关联,发现PRB60(Rub-B的16S,17R立体异构体)具有高达99.2%的DP4+可能性,但同时作者也注意到,尽管该结构1H NMR数据的DP4+可能性为99.8%,但13C NMR数据的DP4+可能性仅为0.5%.作者对原文[91]提供的NMR图谱进行了仔细分析后发现,PRub-B的C-15的错误归属可能是DP4+(C数据)偏低的原因.此外,作者还发现,PRB60的优势构象能较好的解释PRub-B的ROESY谱[91]中的H-1/H-27相关,进一步提示PRB60为PRub-B可能的正确结构.最后,作者也对其它96种可能的非对映异构体进行了计算,DP4+分析的结果依然支持PRB60为PRub-B的正确结构.

|
图 3 pseudo-rubriflordilactone B的原定结构[91]与可能的正确结构[93] Fig. 3 Originally proposed[91] and the possible right structures[93] of pseudo-rubriflordilactone B |
尽管以上结论尚待证实,但该研究仍在一定程度上反映了qcc-NMR结合DP4+可能性分析方法的强大,同时也证实即使有SXRD数据支撑化合物结构,qcc-NMR计算结果仍可以作为一项独立的证据存在.
3.3 DU8+计算应用于天然产物的“高通量纠错”偶合常数对于天然产物的构象及构型研究至关重要,而Kutateladze等[74, 75]开发的rff计算方法(DU8,DU8c)为偶合常数的计算提供了更多选择,近年来在天然产物的结构解析与结构纠正中得到了较为广泛的应用[67, 68, 94-99].Kutateladze等[18]注意到,自然界中含卤原子的天然产物较为丰富,且往往具有良好的生物活性,然而,重原子效应(heavy-atom effects)使被卤原子取代碳原子的δC计算存在诸多挑战,使用常规方法往往难以获得准确的计算结果.受rff方法的启发,Kutateladze等提出了在ωB97x-D/6-31G(d)//B3LYP/6-31G(d)理论水平下计算δC,并对计算结果进行参数化校正的方法,其中校正参数通过一个训练集的计算结果得到,该训练集中的分子结构中至少含有S、Cl、Br和I原子中的一种,作者将这一NMR化学位移参数化计算的方法与rff方法的结合体称为DU8+,并应用这种方法对100个含卤原子化合物的化学结构进行了检验,并纠正了其中16个化合物的结构[67].随后,作者又把NMR化学位移量子化学计算的方法迁移到了常规δC和δH计算中,并再次利用DU8+,对90多个triquinane倍半萜的化学结构进行了检验,发现其中13个化合物的结构需要纠正[68].近日,作者再次利用DU8+对近100个含有环氧乙烷片段化合物的结构进行检验,并纠正了其中21个化合物的结构[100].
以上研究表现了DU8+等将DFT计算与参数化校正结合的方法的独特优势,这一方法性价比较高,且具有良好的可迁移性.此外,值得一提的是,近年来天然产物领域众多学者共同发起了“(核磁共振)原始数据倡议”(Raw Data Initiative),呼吁建立存放天然产物NMR原始数据[如自由感应衰减(free induction decay, FID)数据]的可开放获取数据库,以此来增进天然产物研究的透明度、可重复性及完整性.这一数据库一旦成行,即有可能通过机器学习等方法对未经人为干预的NMR原始数据进行自动化数据提取.进而,利用这些数据,并借助计算机辅助结构解析(computer-assisted structure elucidation,CASE)及qcc-NMR等方法,对已发表天然产物的结构进行更大规模的检验[101, 102].
3.4 qcc-NMR与手性光学性质量子化学计算的联用通过量子化学计算天然产物的手性光学性质(chiroptical properties),如ECD、振动圆二色谱(vibrational circular dichroism,VCD)、ORD等,在天然产物的构型确定中也具有不可替代的重要地位[103-105].ECD、VCD等光谱往往能提供与绝对构型确定相关的信息,但对于ECD、VCD等计算结果的评价往往基于图形对比,且适用性往往对化学结构中发色团等性质有不同程度的要求.此外,尽管对旋光计算结果的评价也是基于数值对比,但其实测值与计算值的精确度均受到很多因素影响,因而实用性受到一定限制[106].qcc-NMR的优势已在上文详述,但大多数情况下其仅能辅助天然产物相对构型的确定.因而,将qcc-NMR与手性光学性质量子化学计算联合使用,可以优势互补.如Pereda-Miranda等[107]在对短柄吊球草(Hyptis brevipes)的植物化学成分研究中,分离得到5个具有显著肿瘤细胞毒活性的化合物——Brevipolides K~O,它们都具有柔性结构及多手性中心,因而构型确定具有较大难度,作者通过化学位移、偶合常数和ECD计算,结合细致的图谱分析及Mosher法等,成功的确定了以上化合物的绝对构型(图 4).
各种计算方法的联合使用往往能使各种基于不同原理的证据互相支撑,对于天然结构解析具有重要意义.
3.5 qcc-NMR与CASE的联用在以上qcc-NMR应用实例中,都存在一个必要前提,即操作者已结合NMR图谱及其它手段解析出化合物可能的结构.然而,NMR谱图的解析很大程度上依赖于解析者对于谱图信息的理解,因而解析结果的正确性受到诸多因素的影响.同时,因为信息有限而无法得出可能结构的情况也较为常见.CASE专家系统则较好地解决了这一问题,ACD/Structure Elucidator专家系统是其中的优秀代表.CASE专家系统根据使用者提供的NMR数据,能依靠严格的算法穷举所有可能的结构,进而基于经验方法(如HOSE code、神经网络或增量法等)对各结构的NMR化学位移进行预测,并根据预测值与实测值的差异大小对所有结构进行排列.此外,相对于量子化学计算,CASE专家系统在计算速度上也具有绝对的优势.然而,尽管CASE在天然产物解析中有诸多成功案例,但实际应用中也常存在以下非理想情景:(1)CASE未将正确结构列于首位,其NMR化学位移的预测值的平均偏差较大;(2)正确结构被CASE排列于首位或靠前位置,但排列靠前的各结构偏差接近.此时,qcc-NMR的参与往往能较好的解决以上问题.近期,默克公司的Buevich与ACD/Labs公司的Elyashberg应用以上思路,对3个极具挑战的天然产物分子进行了案例分析[108],以此证明了qcc-NMR与CASE的联用可用于复杂的结构解析问题,并能提供可靠的结果.
4 结论量子化学计算方法在天然产物研究中的作用越来越重要[109],而NMR波谱在天然产物结构解析中的重要地位也促使qcc-NMR成为了天然产物研究中的一项重要工具,并可以作为辅助天然产物结构解析或有机合成前验证目标分子正确性的常规方法.尽管如此,当前qcc-NMR方法仍不可避免地存在局限性,例如,构象质量、计算使用的理论水平、溶剂模型等因素均对计算结果的准确性存在不同程度的影响,尤其对于柔性较大的分子,由于构象众多,且在有限基组下构象能量计算并不准确,常常很难获得准确的计算结果.鉴于此,qcc-NMR方法与其它结构解析技术的联合使用就显得尤为重要.事实上,随着各种结构解析技术的不断发展,天然产物结构解析的“工具箱”也在日益强大,近年来颇具代表性的发展方向有各向异性核磁(anisotropic NMR)[110-112]、晶体海绵法(crystalline sponge method)[113-115]等.对于复杂天然产物的结构解析,应用多种手段从而达到优势互补、互相佐证的目的已成为一种趋势,如homodimericin A[116]、caulamidines A和B[117]的结构解析即是其中的典型代表.综上所述,qcc-NMR在天然产物结构解析中有着广阔的应用空间,与其它技术结合使用,能为天然产物的结构解析提供强有力的支撑,从而为后续研究的顺利开展提供保障.
| [1] | NEWMAN D J, CRAGG G M. Natural products as sources of new drugs from 1981 to 2014[J]. J Nat Prod, 2016, 79(3): 629-661. |
| [2] | BRETON R C, REYNOLDS W F. Using NMR to identify and characterize natural products[J]. Nat Prod Rep, 2013, 30(4): 501-524. DOI: 10.1039/c2np20104f. |
| [3] |
WANG B, LIU X, ZHU G L, et al. Applications of new two-dimensional NMR spectroscopy in natural products research[J].
Chinese J Magn Reson, 2013, 30(4): 602-613.
王蓓, 刘星, 朱国磊, 等. 新二维核磁共振谱在天然产物研究中的应用[J]. 波谱学杂志, 2013, 30(4): 602-613. DOI: 10.3969/j.issn.1000-4556.2013.04.014. |
| [4] | REYNOLDS W F. Natural product structure elucidation by NMR spectroscopy[M]//BADAL S, DELGODA R. Pharmacognosy. Boston: Academic Press, 2017: 567-596. |
| [5] |
SUN L J, HU X F, C X, et al. NMR characterization of flavanone naringenin 7-O-glycoside diastereomer[J].
Chinese J Magn Reson, 2017, 34(4): 465-473.
孙丽娟, 胡小芳, 程寻, 等. 柚皮素7-O-葡萄糖苷非对映异构体的NMR波谱分析[J]. 波谱学杂志, 2017, 34(4): 465-473. |
| [6] |
YIN T P, CHEN Y, LUO P, et al. Structural elucidation and NMR spectral assignments of two C19-diterpenoid alkaloids[J].
Chinese J Magn Reson, 2018, 35(1): 90-97.
尹田鹏, 陈阳, 罗萍, 等. 两个C19-二萜生物碱的结构鉴定和NMR信号归属[J]. 波谱学杂志, 2018, 35(1): 90-97. |
| [7] | HALABALAKI M, VOUGOGIANNOPOULOU K, MIKROS E, et al. Recent advances and new strategies in the NMR-based identification of natural products[J]. Curr Opin in Biotech, 2014, 25: 1-7. DOI: 10.1016/j.copbio.2013.08.005. |
| [8] | MENNA M, IMPERATORE C, MANGONI A, et al. Challenges in the configuration assignment of natural products. A case-selective perspective[J]. Nat Prod Rep, 2019, 36(3): 476-489. DOI: 10.1039/C8NP00053K. |
| [9] | NICOLAOU K C, SNYDER S A. Chasing molecules that were never there: misassigned natural products and the role of chemical synthesis in modern structure elucidation[J]. Angew Chem Int Ed, 2005, 44(7): 1012-1044. DOI: 10.1002/anie.200460864. |
| [10] | SUYAMA T L, GERWICK W H, MCPHAIL K L. Survey of marine natural product structure revisions: A synergy of spectroscopy and chemical synthesis[J]. Bioorg Med Chem, 2011, 19(22): 6675-6701. DOI: 10.1016/j.bmc.2011.06.011. |
| [11] | YOO H D, NAM S J, CHIN Y W, et al. Misassigned natural products and their revised structures[J]. Arch Pharm Res, 2016, 39(2): 143-153. DOI: 10.1007/s12272-015-0649-9. |
| [12] | CHHETRI B K, LAVOIE S, SWEENEY-JONES A M, et al. Recent trends in the structural revision of natural products[J]. Nat Prod Rep, 2018, 35(6): 514-531. DOI: 10.1039/C8NP00011E. |
| [13] | BARONE G, DUCA D, SILVESTRI A, et al. Determination of the relative stereochemistry of flexible organic compounds by ab initio methods: conformational analysis and Boltzmann-averaged GIAO 13C NMR chemical shifts[J]. Chem-Eur J, 2002, 8(14): 3240-3245. DOI: 10.1002/1521-3765(20020715)8:14<3240::AID-CHEM3240>3.0.CO;2-G. |
| [14] | BARONE G, GOMEZ-PALOMA L, DUCA D, et al. Structure validation of natural products by quantum‐mechanical GIAO calculations of 13C NMR chemical shifts[J]. Chem-Eur J, 2002, 8(14): 3233-3239. DOI: 10.1002/1521-3765(20020715)8:14<3233::AID-CHEM3233>3.0.CO;2-0. |
| [15] | GRIMBLAT N, SAROTTI A M. Computational chemistry to the rescue: modern toolboxes for the assignment of complex molecules by GIAO NMR calculations[J]. Chem-Eur J, 2016, 22(35): 12246-12261. DOI: 10.1002/chem.201601150. |
| [16] | BIFULCO G, DAMBRUOSO P, GOMEZ-PALOMA L, et al. Determination of relative configuration in organic compounds by NMR spectroscopy and computational methods[J]. Chem Rev, 2007, 107(9): 3744-3779. DOI: 10.1021/cr030733c. |
| [17] | DI MICCO S, CHINI M G, RICCIO R, et al. Quantum mechanical calculation of NMR parameters in the stereostructural determination of natural products[J]. Eur J Org Chem, 2010, 2010(8): 1411-1434. DOI: 10.1002/ejoc.200901255. |
| [18] | LODEWYK M W, SIEBERT M R, TANTILLO D J. Computational prediction of 1H and 13C chemical shifts: a useful tool for natural product, mechanistic, and synthetic organic chemistry[J]. Chem Rev, 2012, 112(3): 1839-1862. |
| [19] | BAGNO A, SAIELLI G. Addressing the stereochemistry of complex organic molecules by density functional theory-NMR[J]. Wires Comput Mol Sci, 2015, 5(2): 228-240. DOI: 10.1002/wcms.1214. |
| [20] |
GU B B, LIN H W. Quantum chemical calculation of 1H and 13C chemical shifts and 1H-1H coupling constants in structure assignment of natural products[J].
Journal of International Pharmaceutical Research, 2015, 42(6): 706-712.
顾斌斌, 林厚文. 量子化学计算1H和13C化学位移与1H-1H偶合常数在天然产物结构鉴定中的运用[J]. 国际药学研究杂志, 2015, 42(6): 706-712. |
| [21] | NAVARRO-VAZQUEZ A. State of the art and perspectives in the application of quantum chemical prediction of 1H and 13C chemical shifts and scalar couplings for structural elucidation of organic compounds[J]. Magn Reson Chem, 2017, 55(1): 29-32. |
| [22] | TANG Y, XUE Y, DU G, et al. Structural revisions of a class of natural products: scaffolds of aglycon analogues of fusicoccins and cotylenins isolated from fungi[J]. Angew Chem Int Ed, 2016, 55(12): 4069-4073. DOI: 10.1002/anie.201600313. |
| [23] | SAROTTI A M. Structural revision of two unusual rhamnofolane diterpenes, curcusones I and J, by means of DFT calculations of NMR shifts and coupling constants[J]. Org Biomol Chem, 2018, 16(6): 944-950. DOI: 10.1039/C7OB02916K. |
| [24] | GRIMBLAT N, ZANARDI M M, SAROTTI A M. Beyond DP4: an improved probability for the stereochemical assignment of isomeric compounds using quantum chemical calculations of NMR shifts[J]. J Org Chem, 2015, 80(24): 12526-12534. DOI: 10.1021/acs.joc.5b02396. |
| [25] | SECO J M, QUINOA E, RIGUERA R. Assignment of the absolute configuration of polyfunctional compounds by NMR using chiral derivatizing agents[J]. Chem Rev, 2012, 112(8): 4603-4641. DOI: 10.1021/cr2003344. |
| [26] | ZANARDI M M, BIGLIONE F A, SORTINO M A, et al. General quantum-based NMR method for the assignment of absolute configuration by single or double derivatization: Scope and limitations[J]. J Org Chem, 2018, 83(19): 11839-11849. DOI: 10.1021/acs.joc.8b01749. |
| [27] | SHI Y M, CAI S L, LI X N, et al. LC-UV-guided isolation and structure determination of lancolide E: a nortriterpenoid with a tetracyclo[5.4.0.02, 4.03, 7]undecane-bridged system from a "talented" schisandra plant[J]. Org Lett, 2016, 18(1): 100-103. DOI: 10.1021/acs.orglett.5b03334. |
| [28] | WILLOUGHBY P H, JANSMA M J, HOYE T R. A guide to small-molecule structure assignment through computation of 1H and 13C NMR chemical shifts[J]. Nat Protoc, 2014, 9(3): 643-660. DOI: 10.1038/nprot.2014.042. |
| [29] | FRISCH M J, TRUCKS G W, SCHLEGEL H B, et al. Gaussian 16 Rev. B.01[CP]. Wallingford, CT: 2016. |
| [30] | NEESE F. Software update: the ORCA program system, version 4.0[J]. Wires Comput Mol Sci, 2018, 8(1): e1327. DOI: 10.1002/wcms.1327. |
| [31] | AIDAS K, ANGELI C, BAK K L, et al. The Dalton quantum chemistry program system[J]. Wires Comput Mol Sci, 2014, 4(3): 269-284. DOI: 10.1002/wcms.1172. |
| [32] | HAWKINS P C D. Conformation generation: the state of the art[J]. J Chem Inf Model, 2017, 57(8): 1747-1756. DOI: 10.1021/acs.jcim.7b00221. |
| [33] | VAINIO M J, JOHNSON M S. Generating conformer ensembles using a multiobjective genetic algorithm[J]. J Chem Inf Model, 2007, 47(6): 2462-2474. DOI: 10.1021/ci6005646. |
| [34] | MITEVA M A, GUYON F, TUFFéRY P. Frog2: Efficient 3D conformation ensemble generator for small compounds[J]. Nucleic Acids Res, 2010, 38(Web Server issue): W622-W627. |
| [35] | CASE D A, CHEATHAM T E, DARDEN T, et al. The Amber biomolecular simulation programs[J]. J Comput Chem, 2005, 26(16): 1668-1688. DOI: 10.1002/jcc.20290. |
| [36] | SPOEL D V D, LINDAHL E, HESS B, et al. GROMACS: fast, flexible, and free[J]. J Comput Chem, 2005, 26(16): 1701-1718. DOI: 10.1002/jcc.20291. |
| [37] | GRIMME S, BANNWARTH C, SHUSHKOV P. A robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent interactions of large molecular systems parametrized for all spd-block elements (Z=1–86)[J]. J Chem Theory Comput, 2017, 13(5): 1989-2009. DOI: 10.1021/acs.jctc.7b00118. |
| [38] | HALGREN T A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94[J]. J Comput Chem, 1996, 17(5, 6): 490-519. |
| [39] | BANKS J L, BEARD H S, CAO Y, et al. Integrated modeling program, applied chemical theory (IMPACT)[J]. J Comput Chem, 2005, 26(16): 1752-1780. DOI: 10.1002/jcc.20292. |
| [40] | STEWART J J P. Optimization of parameters for semiempirical methods Ⅴ: Modification of NDDO approximations and application to 70 elements[J]. J Mol Model, 2007, 13(12): 1173-1213. DOI: 10.1007/s00894-007-0233-4. |
| [41] | STEPHENS P J, DEVLIN F J, CHABALOWSKI C F, et al. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields[J]. J Phys Chem, 1994, 98(45): 11623-11627. DOI: 10.1021/j100096a001. |
| [42] | ZHAO Y, TRUHLAR D G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals[J]. Theor Chem Acc, 2008, 120(1): 215-241. |
| [43] | CHAI J D, HEAD-GORDON M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections[J]. PCCP, 2008, 10(44): 6615-6620. DOI: 10.1039/b810189b. |
| [44] | GRIMME S, ANTONY J, EHRLICH S, et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu[J]. J Chem Phys, 2010, 132(15): 154104. DOI: 10.1063/1.3382344. |
| [45] | RASSOLOV V A, RATNER M A, POPLE J A, et al. 6-31G* basis set for third-row atoms[J]. J Comput Chem, 2001, 22(9): 976-984. DOI: 10.1002/jcc.1058. |
| [46] | KRISHNAN R, BINKLEY J S, SEEGER R, et al. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions[J]. J Chem Phys, 1980, 72(1): 650-654. |
| [47] | SCH FER A, HORN H, AHLRICHS R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr[J]. J Chem Phys, 1992, 97(4): 2571-2577. |
| [48] | SCH FER A, HUBER C, AHLRICHS R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr[J]. J Chem Phys, 1994, 100(8): 5829-5835. DOI: 10.1063/1.467146. |
| [49] | BUTTS C P, JONES C R, TOWERS E C, et al. Interproton distance determinations by NOE-surprising accuracy and precision in a rigid organic molecule[J]. Org Biomol Chem, 2011, 9(1): 177-184. |
| [50] | BUTTS C P, JONES C R, SONG Z, et al. Accurate NOE-distance determination enables the stereochemical assignment of a flexible molecule-arugosin C[J]. Chem Commun, 2012, 48(72): 9023-9025. DOI: 10.1039/c2cc32144k. |
| [51] | JONES C R, GREENHALGH M D, BAME J R, et al. Subtle temperature-induced changes in small molecule conformer dynamics-observed and quantified by NOE spectroscopy[J]. Chem Commun, 2016, 52(14): 2920-2923. DOI: 10.1039/C5CC10509A. |
| [52] | FACELLI J C. Calculations of chemical shieldings: theory and applications[J]. Concept Magn Reson Part A, 2004, 20A(1): 42-69. DOI: 10.1002/cmr.a.10096. |
| [53] | DITCHFIELD R. Self-consistent perturbation theory of diamagnetism[J]. Mol Phys, 1974, 27(4): 789-807. |
| [54] | KEITH T A, BADER R F W. Calculation of magnetic response properties using a continuous set of gauge transformations[J]. Chem Phys Lett, 1993, 210(1): 223-231. |
| [55] | FLAIG D, MAURER M, HANNI M, et al. Benchmarking hydrogen and carbon NMR chemical shifts at HF, DFT, and MP2 levels[J]. J Chem Theory Comput, 2014, 10(2): 572-578. |
| [56] | IRON M A. Evaluation of the factors impacting the accuracy of 13C NMR chemical shift predictions using density functional theory-the advantage of long-range corrected functionals[J]. J Chem Theory Comput, 2017, 13(11): 5798-5819. DOI: 10.1021/acs.jctc.7b00772. |
| [57] | WⅡTALA K W, HOYE T R, CRAMER C J. Hybrid density functional methods empirically optimized for the computation of 13C and 1H chemical shifts in chloroform solution[J]. J Chem Theory Comput, 2006, 2(4): 1085-1092. |
| [58] | BROWN S G, JANSMA M J, HOYE T R. Case study of empirical and computational chemical shift analyses: reassignment of the relative configuration of phomopsichalasin to that of diaporthichalasin[J]. J Nat Prod, 2012, 75(7): 1326-1331. DOI: 10.1021/np300248w. |
| [59] | KEAL T W, TOZER D J. The exchange-correlation potential in Kohn-Sham nuclear magnetic resonance shielding calculations[J]. J Chem Phys, 2003, 119(6): 3015-3024. |
| [60] | ADAMO C, BARONE V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models[J]. J Chem Phys, 1998, 108(2): 664-675. |
| [61] | WILSON P J, BRADLEY T J, TOZER D J. Hybrid exchange-correlation functional determined from thermochemical data and ab initio potentials[J]. J Chem Phys, 2001, 115(20): 9233-9242. DOI: 10.1063/1.1412605. |
| [62] | ADAMO C, BARONE V. Toward reliable density functional methods without adjustable parameters: The PBE0 model[J]. J Chem Phys, 1999, 110(13): 6158-6170. DOI: 10.1063/1.478522. |
| [63] | JENSEN F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods[J]. J Chem Theory Comput, 2008, 4(5): 719-727. DOI: 10.1021/ct800013z. |
| [64] | JENSEN F. Unifying general and segmented contracted basis sets[J]. J Chem Theory Comput, 2014, 10(3): 1074-1085. |
| [65] | GRIMME S, BANNWARTH C, DOHM S, et al. Fully automated quantum-chemistry-based computation of spin-spin-coupled nuclear magnetic resonance spectra[J]. Angew Chem Int Ed, 2017, 56(46): 14763-14769. DOI: 10.1002/anie.201708266. |
| [66] | XIN D, SADER C A, CHAUDHARY O, et al. Development of a 13C NMR chemical shift prediction procedure using B3LYP/cc-pVDZ and empirically derived systematic error correction terms: a computational small molecule structure elucidation method[J]. J Org Chem, 2017, 82(10): 5135-5145. DOI: 10.1021/acs.joc.7b00321. |
| [67] | KUTATELADZE A G, REDDY D S. High-throughput in silico structure validation and revision of halogenated natural products Is enabled by parametric corrections to DFT-computed 13C NMR chemical shifts and spin-spin coupling constants[J]. J Org Chem, 2017, 82(7): 3368-3381. DOI: 10.1021/acs.joc.7b00188. |
| [68] | KUTATELADZE A G, KUZNETSOV D M. Triquinanes and related sesquiterpenes revisited computationally: structure corrections of hirsutanols B and D, hirsutenol E, cucumin B, antrodins C-E, chondroterpenes A and H, chondrosterins C and E, dichrocephone A, and pethybrene[J]. J Org Chem, 2017, 82(20): 10795-10802. DOI: 10.1021/acs.joc.7b02018. |
| [69] | STOYCHEV G L, AUER A A, IZSáK R, et al. Self-consistent field calculation of nuclear magnetic resonance chemical shielding constants using Gauge-Including Atomic Orbitals and approximate two-electron integrals[J]. J Chem Theory Comput, 2018, 14(2): 619-637. |
| [70] | SAROTTI A M, PELLEGRINET S C. A multi-standard approach for GIAO (13)C NMR calculations[J]. J Org Chem, 2009, 74(19): 7254-7260. DOI: 10.1021/jo901234h. |
| [71] | SAROTTI A M, PELLEGRINET S C. Application of the multi-standard methodology for calculating 1H NMR chemical shifts[J]. J Org Chem, 2012, 77(14): 6059-6065. DOI: 10.1021/jo3008447. |
| [72] | BALLY T, RABLEN P R. Quantum-chemical simulation of 1H NMR spectra. 2. Comparison of DFT-based procedures for computing proton-proton coupling constants in organic molecules[J]. J Org Chem, 2011, 76(12): 4818-4830. DOI: 10.1021/jo200513q. |
| [73] | MATSUMORI N, KANENO D, MURATA M, et al. Stereochemical determination of acyclic structures based on carbon-proton spin-coupling constants. A method of configuration analysis for natural products[J]. J Org Chem, 1999, 64(3): 866-876. |
| [74] | KUTATELADZE A G, MUKHINA O A. Relativistic force field: parametric computations of proton-proton coupling constants in 1H NMR spectra[J]. J Org Chem, 2014, 79(17): 8397-8406. DOI: 10.1021/jo501781b. |
| [75] | KUTATELADZE A G, MUKHINA O A. Relativistic force field: parametrization of 13C-1H nuclear spin-spin coupling constants[J]. J Org Chem, 2015, 80(21): 10838-10848. DOI: 10.1021/acs.joc.5b02001. |
| [76] | BIFULCO G, BASSARELLO C, RICCIO R, et al. Quantum mechanical calculations of NMR J coupling values in the determination of relative configuration in organic compounds[J]. Org Lett, 2004, 6(6): 1025-1028. DOI: 10.1021/ol049913e. |
| [77] | JENSEN F. The optimum contraction of basis sets for calculating spin-spin coupling constants[J]. Theor Chem Acc, 2010, 126(5): 371-382. |
| [78] | SMITH S G, GOODMAN J M. Assigning the stereochemistry of pairs of diastereoisomers using GIAO NMR shift calculation[J]. J Org Chem, 2009, 74(12): 4597-4607. DOI: 10.1021/jo900408d. |
| [79] | SMITH S G, GOODMAN J M. Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: the DP4 probability[J]. J Am Chem Soc, 2010, 132(37): 12946-12959. DOI: 10.1021/ja105035r. |
| [80] | XIN D, JONES P J, GONNELLA N C. DiCE: diastereomeric in silico chiral elucidation, expanded DP4 probability theory method for diastereomer and structural assignment[J]. J Org Chem, 2018, 83(9): 5035-5043. DOI: 10.1021/acs.joc.8b00338. |
| [81] | ERMANIS K, PARKES K E, AGBACK T, et al. Expanding DP4: application to drug compounds and automation[J]. Org Biomol Chem, 2016, 14(16): 3943-3949. DOI: 10.1039/C6OB00015K. |
| [82] | ERMANIS K, PARKES K E B, AGBACK T, et al. Doubling the power of DP4 for computational structure elucidation[J]. Org Biomol Chem, 2017, 15(42): 8998-9007. DOI: 10.1039/C7OB01379E. |
| [83] | SAROTTI A M. Successful combination of computationally inexpensive GIAO 13C NMR calculations and artificial neural network pattern recognition: a new strategy for simple and rapid detection of structural misassignments[J]. Org Biomol Chem, 2013, 11(29): 4847-4859. DOI: 10.1039/c3ob40843d. |
| [84] | ZANARDI M M, SAROTTI A M. GIAO C-H COSY simulations merged with artificial neural networks pattern recognition analysis. Pushing the structural validation a step forward[J]. J Org Chem, 2015, 80(19): 9371-9378. DOI: 10.1021/acs.joc.5b01663. |
| [85] | KIM C S, SUBEDI L, OH J, et al. Bioactive triterpenoids from the twigs of Chaenomeles sinensis[J]. J Nat Prod, 2017, 80(4): 1134-1140. DOI: 10.1021/acs.jnatprod.7b00111. |
| [86] | ZANARDI M M, SUáREZ A G, SAROTTI A M. Determination of the relative configuration of terminal and spiroepoxides by computational methods. Advantages of the inclusion of unscaled data[J]. J Org Chem, 2017, 82(4): 1873-1879. |
| [87] | XIN D, SADER C A, FISCHER U, et al. Systematic investigation of DFT-GIAO 15N NMR chemical shift prediction using B3LYP/cc-pVDZ: application to studies of regioisomers, tautomers, protonation states and N-oxides[J]. Org Biomol Chem, 2017, 15(4): 928-936. |
| [88] | TRIPATHI A, SCHOFIELD M M, CHLIPALA G E, et al. Baulamycins A and B, broad-spectrum antibiotics identified as inhibitors of siderophore biosynthesis in Staphylococcus aureus and Bacillus anthracis[J]. J Am Chem Soc, 2014, 136(4): 1579-1586. DOI: 10.1021/ja4115924. |
| [89] | GUCHHAIT S, CHATTERJEE S, AMPAPATHI R S, et al. Total synthesis of reported structure of baulamycin A and Its congeners[J]. J Org Chem, 2017, 82(5): 2414-2435. DOI: 10.1021/acs.joc.6b02838. |
| [90] | WU J, LORENZO P, ZHONG S, et al. Synergy of synthesis, computation and NMR reveals correct baulamycin structures[J]. Nature, 2017, 547(7664): 436-440. DOI: 10.1038/nature23265. |
| [91] | XIAO W L, YANG L M, GONG N B, et al. Rubriflordilactones A and B, two novel bisnortriterpenoids from Schisandra rubriflora and their biological activities[J]. Org Lett, 2006, 8(5): 991-994. DOI: 10.1021/ol060062f. |
| [92] | YANG P, YAO M, LI J, et al. Total synthesis of rubriflordilactone B[J]. Angew Chem Int Ed, 2016, 55(24): 6964-6968. DOI: 10.1002/anie.201601915. |
| [93] | GRIMBLAT N, KAUFMAN T S, SAROTTI A M. Computational chemistry driven solution to rubriflordilactone B[J]. Org Lett, 2016, 18(24): 6420-6423. DOI: 10.1021/acs.orglett.6b03318. |
| [94] | KUTATELADZE A G. Structure revision of decurrensides A-E enabled by the RFF parametric calculations of proton spin-spin coupling constants[J]. J Org Chem, 2016, 81(18): 8659-8661. DOI: 10.1021/acs.joc.6b01855. |
| [95] | REDDY D S, KUTATELADZE A G. Structure revision of an acorane sesquiterpene cordycepol A[J]. Org Lett, 2016, 18(19): 4860-4863. DOI: 10.1021/acs.orglett.6b02341. |
| [96] | CHACON MORALES P A, AMARO-LUIS J M, KUTATELADZE A G. Structure determination and mechanism of formation of a seco-moreliane derivative supported by computational analysis[J]. J Nat Prod, 2017, 80(4): 1210-1214. DOI: 10.1021/acs.jnatprod.7b00041. |
| [97] | GU B B, TANG J, WANG S P, et al. Structure, absolute configuration, and variable-temperature 1H-NMR study of (±)-versiorcinols A-C, three racemates of diorcinol monoethers from the sponge-associated fungus Aspergillus versicolor 16F-11[J]. RSC Adv, 2017, 7(79): 50254-50263. DOI: 10.1039/C7RA06106D. |
| [98] | SUN C P, KUTATELADZE A G, ZHAO F, et al. A novel withanolide with an unprecedented carbon skeleton from physalis angulata[J]. Org Biomol Chem, 2017, 15(5): 1110-1114. DOI: 10.1039/C6OB02656G. |
| [99] | WANG C, HUO X K, LUAN Z L, et al. Alismanin A, a triterpenoid with a C34 skeleton from Alisma orientale as a natural agonist of human pregnane X receptor[J]. Org Lett, 2017, 19(20): 5645-5648. DOI: 10.1021/acs.orglett.7b02738. |
| [100] | KUTATELADZE A G, KUZNETSOV D M, BELOGLAZKINA A A, et al. Addressing the challenges of structure elucidation in natural products possessing the oxirane moiety[J]. J Org Chem, 2018, 83(15): 8341-8352. DOI: 10.1021/acs.joc.8b01027. |
| [101] | BISSON J, SIMMLER C, CHEN S N, et al. Dissemination of original NMR data enhances reproducibility and integrity in chemical research[J]. Nat Prod Rep, 2016, 33(9): 1028-1033. DOI: 10.1039/C6NP00022C. |
| [102] | MCALPINE J B, CHEN S N, KUTATELADZE A, et al. The value of universally available raw NMR data for transparency, reproducibility, and integrity in natural product research[J]. Nat Prod Rep, 2019, 36(1): 35-107. DOI: 10.1039/C7NP00064B. |
| [103] | SREBRO-HOOPER M, AUTSCHBACH J. Calculating natural optical activity of molecules from first principles[J]. Annu Rev of Phys Chem, 2017, 68(1): 399-420. DOI: 10.1146/annurev-physchem-052516-044827. |
| [104] | PESCITELLI G, DI BARI L, BEROVA N. Application of electronic circular dichroism in the study of supramolecular systems[J]. Chem Soc Rev, 2014, 43(15): 5211-5233. DOI: 10.1039/C4CS00104D. |
| [105] | STEFANO S, PATRIZIA S, MARCIN G, et al. Absolute configuration determination by quantum mechanical calculation of chiroptical spectra: basics and applications to fungal metabolites[J]. Curr Med Chem, 2018, 25(2): 287-320. |
| [106] | POLAVARAPU P L. Molecular structure determination using chiroptical spectroscopy: Where we may go wrong?[J]. Chirality, 2012, 24(11): 909-920. DOI: 10.1002/chir.22015. |
| [107] | SUAREZ-ORTIZ G A, CERDA-GARCIA-ROJAS C M, FRAGOSO-SERRANO M, et al. Complementarity of DFT calculations, NMR Anisotropy, and ECD for the configurational analysis of brevipolides K-O from Hyptis brevipes[J]. J Nat Prod, 2017, 80(1): 181-189. |
| [108] | BUEVICH A V, ELYASHBERG M E. Synergistic combination of CASE algorithms and DFT chemical shift predictions: a powerful approach for structure elucidation, verification, and revision[J]. J Nat Prod, 2016, 79(12): 3105-3116. DOI: 10.1021/acs.jnatprod.6b00799. |
| [109] | TANTILLO D J. Walking in the woods with quantum chemistry-applications of quantum chemical calculations in natural products research[J]. Nat Prod Rep, 2013, 30(8): 1079-1086. DOI: 10.1039/c3np70028c. |
| [110] | LIU Y, SAURí J, MEVERS E, et al. Unequivocal determination of complex molecular structures using anisotropic NMR measurements[J]. Science, 2017, 356(6333). |
| [111] | NAVARRO-VáZQUEZ A, GIL R R, BLINOV K. Computer-assisted 3D structure elucidation (CASE-3D) of natural products combining isotropic and anisotropic NMR parameters[J]. J Nat Prod, 2018, 81(1): 203-210. |
| [112] | LI G W, LIU H, QIU F, et al. Residual dipolar couplings in structure determination of natural products[J]. Nat Prod Bioprospect, 2018, 8(4): 279-295. DOI: 10.1007/s13659-018-0174-x. |
| [113] | INOKUMA Y, YOSHIOKA S, ARIYOSHI J, et al. X-ray analysis on the nanogram to microgram scale using porous complexes[J]. Nature, 2013: 495461. |
| [114] | MATSUDA Y, MITSUHASHI T, LEE S, et al. Astellifadiene: structure determination by NMR spectroscopy and crystalline sponge method, and elucidation of its niosynthesis[J]. Angew Chem Int Ed, 2016, 55(19): 5785-5788. DOI: 10.1002/anie.201601448. |
| [115] | WADA N, KERSTEN ROLAND D, IWAI T, et al. Crystalline-sponge-based structural analysis of crude natural product extracts[J]. Angew Chem, Int Ed, 2018, 130(14): 3733-3737. DOI: 10.1002/ange.201713219. |
| [116] | MEVERS E, SAURí J, LIU Y, et al. Homodimericin A: a complex hexacyclic fungal metabolite[J]. J Am Chem Soc, 2016, 138(38): 12324-12327. DOI: 10.1021/jacs.6b07588. |
| [117] | MILANOWSKI D J, OKU N, CARTNER L K, et al. Unequivocal determination of caulamidines A and B: application and validation of new tools in the structure elucidation tool box[J]. Chem Sci, 2018, 9(2): 307-314. |
 2019, Vol. 36
2019, Vol. 36 

