2. 北京大学 化学与分子工程学院, 北京 100871;
3. 美国斯伦贝谢Doll实验室, 马萨诸塞州 波士顿剑桥 02143
2. College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China;
3. Schlumberger-Doll Research, Cambridge, MA 02143, USA
核磁共振(NMR)波谱是研究有机分子结构的重要工具之一.但由于设备昂贵,一般实验室拥有的NMR谱仪数量有限,而且绝大部分时间用于科学研究,仅少量机时用于实验教学.若学生的NMR理论和实验基础较为薄弱,则易误操作损坏设备或降低设备性能.另外,NMR实验涉及流程较多,教学耗时较长.因此,针对学生的NMR实验教学难以广泛开展.为使相关的科研人员和学生更好的理解NMR基本原理,有效设置采集参数和进行硬件调节,进而快速高效的实现NMR波谱采集和数据处理训练,本文基于数值计算模拟技术,开发了具备真实NMR波谱仪基本功能的仿真NMR波谱仪VMRS1.0软件.
已有一些科研团队做过NMR波谱仿真相关工作,但主要集中在根据用户输入的化学位移、J偶合信息进行NMR谱图预测方面,包括液体和固体NMR谱图的预测[1-5].这些软件只向用户展示了分子结构和NMR谱图之间的关系,但没有NMR实验的参数设置和具体操作界面,与实际NMR波谱仪有很大区别;另外,其可选择的观测核数量有限,一般为1~5个.国内中国科学技术大学杜江峰课题组[6]应用数值模拟技术,利用NMR量子模拟器对Unruh效应进行了实验模拟,但与NMR谱仪差别较大.Tosner小组[7]基于数值模拟技术开发了仿真固体NMR波谱仪,但完全采用命令行的形式输入分子信息和序列参数,在设备操作界面和仪器系统校正方面没有涉及.据文献查询,目前有两个科研团队开展了仿真NMR波谱仪工作.1988年,Schatz小组[8]开发的NMR仿真器是一种基于物理场景模拟的软件,主要用于直观了解NMR设备结构和培训操作流程.近年来,Nicolas小组[9]采用数值计算模拟技术开发了仿真NMR波谱仪,通过手动输入不超过5个自旋核的分子化学信息后,设定不同序列参数,最后输出谱图结果.这款软件和实际NMR波谱仪的工作过程已经非常近似,但在界面上差异较大,另外也没有涉及NMR实验中耗费时间精力的匀场、锁场、射频脉冲调节等环节.而本文基于数值计算模拟技术开发的VMRS1.0软件,按照NMR实验的实际操作全流程以及真机操作界面,可用于开展类似真机功能的NMR实验教学.
1 系统建模与开发NMR谱仪无论体积如何庞大、价格如何昂贵,都由硬件和软件组成.硬件主要负责对样品进行信号采集,并将采集的信号调制放大后数字化为离散数据发送给软件.软件一方面发出控制指令,控制硬件按照给定的方案采集信号;另一方面接收硬件传送的数据,进行数据处理和结果可视化显示.硬件采集信号必须遵循一定的科学规律,VMRS1.0软件将这一规律进行数学模型建模(包括硬件、样品和方法)后,通过数值计算模拟技术实现数学模型的数据化,再通过图形用户界面(GUI)界面编程进行具体化和可视化.由此可见,VMRS1.0软件和真实NMR波谱仪遵循相同的理论基础,只是将硬件、样品、方法进行了虚拟化,其软件功能和操作过程是相同的.模拟过程中,数学建模是关键环节,其考虑的细节越充分,模型与真实情况越吻合,仿真输出的结果就越接近于实际采样结果.本文设计的VMRS1.0软件除用于谱图仿真外,还力求突破和遍历硬件条件,用于指导仪器开发和进行谱图预测.
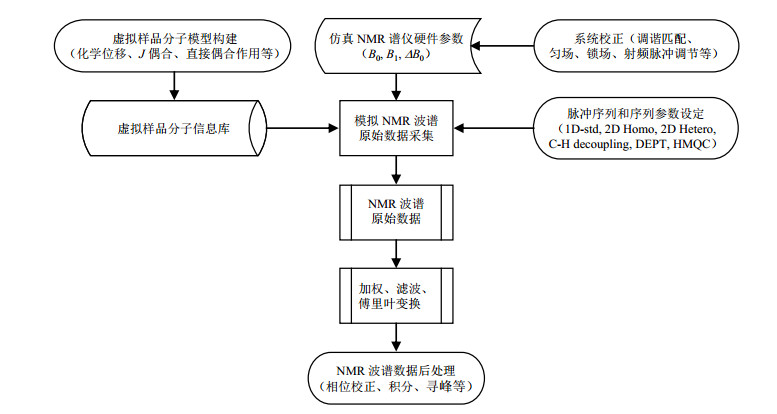
开发过程包括以下几个步骤(图 1所示):首先依次构建虚拟样品分子模型及其信息库、NMR谱仪硬件参数和脉冲序列;然后依据这些信息库和模型,构建模拟NMR谱图原始数据采集的数学模型,通过运行模拟原始数据采集算法和程序,完成原始数据的模拟采集;最后对模拟采集的原始数据进行傅里叶变换(FT)得到NMR谱图,并进行分析与处理,包括相位校正、基线校正、寻峰、积分、测距、化学位移校正等.为了模拟真实NMR实验,VMRS1.0软件还可仿真硬件调节过程,包括自动调谐匹配、匀场、锁场、射频脉冲调节等.
|
图 1 VMRS1.0的开发框架 Fig. 1 Development framework of VMRS1.0 |
本文针对不同的脉冲序列(1D-std、2D Homo、2D Hetero、DEPT等),首先通过量子算符的演化推导得到最终的量子理论表达式,然后转化成经典电磁学模型用于信号采集.
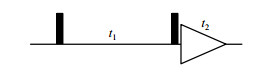
以同核二维相关谱COSY序列(其序列形式如图 2所示)[10]为例:两个90˚脉冲间隔为t1(可变,称为演化期),第二个90˚脉冲实现了极化转移,此后再进行t2维的数据采集.
|
图 2 COSY脉冲序列 Fig. 2 Diagram of COSY pulse sequence |
该序列的信号演化推导过程如下:
第一个90˚脉冲使磁化矢量从z方向翻转到横向:
| ${I_{1z}}\xrightarrow{{{\rm{ \mathit{ π} }}/2{I_{1x}}}}\xrightarrow{{{\rm{ \mathit{ π} }}/2{I_{2x}}}} - {I_{1y}}$ | (1) |
此后在t1时间演化期内,化学位移对自旋体系的作用为:
| $ - {I_{1y}}\xrightarrow{{{\mathit{\Omega} _{\rm{1}}}{t_1}{I_{1z}}}} - \cos {\mathit{\Omega} _1}{t_1}{I_{1y}} + \sin {\mathit{\Omega} _1}{t_1}{I_{1x}}$ | (2) |
J偶合对自旋体系的作用为:
| $\begin{gathered} - \cos {\mathit{\Omega} _1}{t_1}{I_{1y}}\xrightarrow{{2{\rm{ \mathit{ π} }}{J_{12}}{t_1}{I_{1z}}{I_{2z}}}} - \cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}{I_{1y}} + \sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}2{I_{1x}}{I_{2z}} \\ \sin {\mathit{\Omega} _1}{t_1}{I_{1x}}\xrightarrow{{2{\rm{ \mathit{ π} }}{J_{12}}{t_1}{I_{1z}}{I_{2z}}}}\cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}{I_{1x}} + \sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}2{I_{1y}}{I_{2z}} \\ \end{gathered} $ | (3) |
t1演化期后,第二个90˚脉冲对(3)式右边的四项进行作用.逐项作用结果如下:
| $ - \cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}{I_{1y}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{1x}}}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{2x}}}} - \cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}{I_{1z}}$ | (4) |
| $\sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}2{I_{1x}}{I_{2z}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{1x}}}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{2x}}}} - \sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\cos {\mathit{\Omega} _1}{t_1}2{I_{1x}}{I_{2y}}$ | (5) |
| $\cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}{I_{1x}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{1x}}}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{2x}}}}\cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}{I_{1x}}$ | (6) |
| $\sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}2{I_{1y}}{I_{2z}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{1x}}}}\xrightarrow{{{\rm{ \mathit{ π} /2}}{I_{2x}}}} - \sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1}2{I_{1z}}{I_{2y}}$ | (7) |
其中(4)式和(5)式分别为零量子和双量子相干项,信号无法观测到,可以忽略.(6)式反应的是spin1的同相相干,相位为x.该项在t1维调制的主要是spin1的化学位移,因此其信号体现为以
进一步对(6)式通过三角公式进行变形为:
| $\cos {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1} = 1/2[\sin ({\mathit{\Omega} _1}{t_1} + {\rm{ \mathit{ π} }}{J_{12}}{t_1}) + \sin ({\mathit{\Omega} _1}{t_1} - {\rm{ \mathit{ π} }}{J_{12}}{t_1})]$ | (8) |
其信号表示为以
对(7)式可通过三角公式进行变形为:
| $\sin {\rm{ \mathit{ π} }}{J_{12}}{t_1}\sin {\mathit{\Omega} _1}{t_1} = 1/2[ - \cos ({\mathit{\Omega} _1}{t_1} + {\rm{ \mathit{ π} }}{J_{12}}{t_1}) + \cos ({\mathit{\Omega} _1}{t_1} - {\rm{ \mathit{ π} }}{J_{12}}{t_1})]$ | (9) |
其信号表示为以
以上仅对spin1的信号幅度进行了演化推导.具体模拟信号采集时,需考虑每个自选体系内每个自旋核的演化.同时还需要考虑多自旋之间的J偶合导致的谱线多重裂分的频率和幅值效应(即J偶合裂分峰幅值项、J偶合裂分峰频率项)、自身化学位移导致的频率项(即化学位移项)、旋转坐标系数据采集项、T2弛豫项和T1弛豫项、磁化矢量翻转项(含B1不均匀性影响),以及T2*弛豫项(含B0不均匀性影响),将前述各项连乘,分别获得每一种自旋核信号.然后,将每个自旋体系下的多个自旋核信号进行连加,得到累加后的每个自旋体系信号.最后,将多个自旋体系信号进行连加,再叠加模拟随机噪声,即可得到模拟采集的NMR波谱原始数据.
1.2 数据处理VMRS1.0软件对模拟采集得到的NMR波谱原始数据的处理过程与真实NMR谱仪一致,包括FT前处理、FT和FT后处理.FT前处理包括填零,窗函数处理(矩形窗、正弦钟形窗、指数窗等);FT实现从采集数据到谱图的变换;FT后处理包括相位校正、基线校正、寻峰、积分、测距、化学位移校正等.
1.3 GUI界面开发在前述各项建模完成后,用matlab2016a软件进行GUI界面开发.本文设计的VMRS1.0软件选择与Bruker公司topspin V2.0相同的界面布局和按钮,进样(Insert)、出样(Eject),以及数据采集刷新速度受设置参数控制等功能的开发,使其获得了与真实NMR实验类似的操作体验.
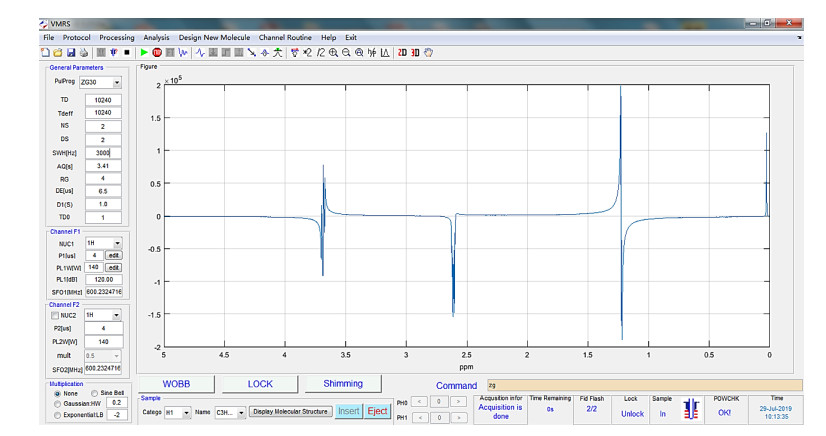
2 结果 2.1 VMRS1.0软件主界面与功能开发成功的VMRS1.0软件的主界面如图 3所示,具体功能包括:选择虚拟样品(软件包包含8种模拟13C NMR谱图和8种模拟1H NMR谱图采集的虚拟样品.另可由用户自行编辑虚拟样品);进样和出样;系统校正,例如自动调谐匹配WOBB、匀场Shimming、锁场LOCK、射频脉冲调节等;选择脉冲序列,如单脉冲序列、去偶序列、COSY序列、DEPT序列、1H-13C HSQC序列等8种序列,并设置相应参数;模拟数据采集;进行数据处理,如FT前处理、FT、FT后处理,以及谱图可视化.该软件包可开展系统校正、操作、参数设置、谱图处理、谱图解析等相关实验至少8个.
|
图 3 VMRS1.0主界面 Fig. 3 The main interface of VMRS1.0 |
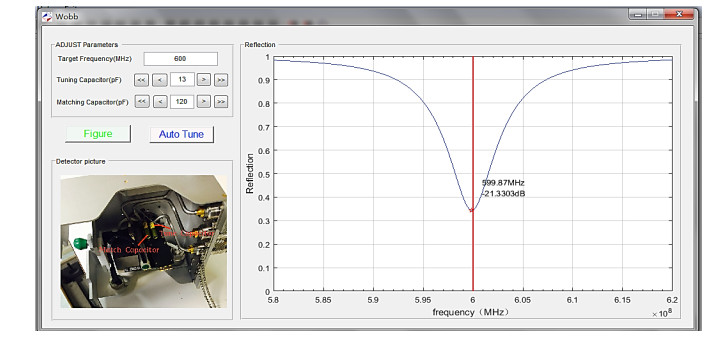
调谐界面如图 4所示:设置目标调谐频率后,目标频率处会显示一条红色竖线;手动调节(粗调》/细调〉)调谐电容和匹配电容,可观察到谐振点偏移和反射曲线锐度调整.细调两个电容,可以使得反射曲线的峰值落在红线上,此时曲线锐度最高、显示的分贝值最小.也可以单击自动调谐按钮,VMRS1.0软件即可自动计算出最佳的调谐电容和匹配电容,且反射曲线显示为最佳状态.
|
图 4 调谐功能界面 Fig. 4 The interface of WOBB |
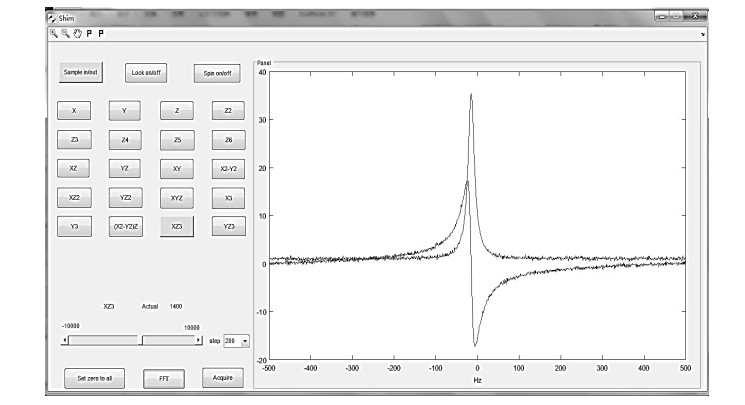
匀场界面如图 5所示.点击匀场线圈Z,此时Z按钮变绿色,表示为正在调节该线圈,同时界面下面的调节滑动条显示为Z,实际调节值也显示为Z线圈的实际调节电流.调节电流滑动条(可在粗调/细调/微调三档切换),可以发现右边的自由感应衰减(FID)信号拖尾会轻微变化,同时FID信号的积分面积数值会出现相应增减,数值增加表示磁场均匀度在优化,则继续向该方向调节电流;反之则表示磁场均匀性降低,则反向调节.调节Z电流至FID积分至最大,表示Z线圈的电流暂时已达到最优.
|
图 5 匀场调节界面 Fig. 5 The interface of Shimming adjustment |
再单击匀场线圈X,X按钮变绿色,表示调节X线圈电流有效.与上面调节过程类似,使FID积分面积最大,表示X线圈的电流暂时已达到最优.再依次调节其余18组线圈.最后再次调节X、Y、Z等,直至FID积分值最大.此时若FT观察频谱,可观察到谱峰变窄,谱图分辨率得以提高.
如果单击spin on/off使其按钮变绿后,X和Y方向磁场的不均匀性值为0,此时任意X和Y方向磁场的调节都会使磁场均匀性降低.
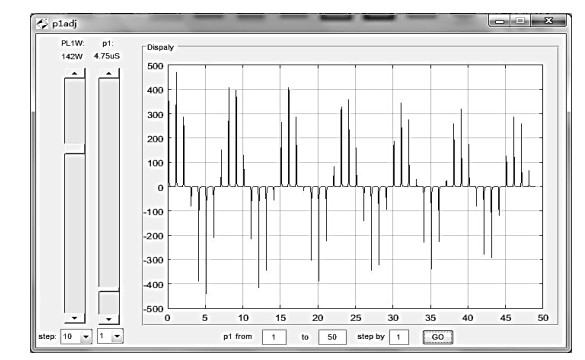
2.2.3 射频脉冲调节功能如图 6所示,调节射频脉冲功率PL1W滑动条,其功率值出现变化,右侧信号频谱幅值也会按照射频翻转角度与信号幅度之间的变换规律变化.调节射频脉冲宽度p1滑动条,其脉宽值出现变化,右侧信号频谱幅值也按照射频翻转角度与信号幅度之间的变换规律变化.设定min-p1、max-p1以及步进值后,单击GO按钮,右侧会分别出现不同p1值下的谱图峰值,峰值变化与射频翻转角度和信号幅度之间遵循正弦变化规律,即为章动谱;基于章动谱可以观察计算射频场B1的不均匀程度.
|
图 6 射频脉冲调节界面 Fig. 6 The interface of radio frequency pulse adjustment |
从分子库中选择不同的分子样品(以乙醇为例)进行波谱数据模拟采集和FT后,其实部谱图不全为吸收线型,也会出现色散线型.在主界面上单击相位校正按钮后,出现一条十字线,用途是确定待调节的pivot,在某一组峰处单击左键,即完成设置0阶校正主峰pivot,pivot一般设置在最高峰附近,也可设置其它峰作为pivot;此后,增加或减少零阶相位PL0,观察pivot峰形变化,直至pivot峰显示为标准的吸收线型,即停止调节PL0;此后再增加或减少一阶相位PL1,观察其它峰形变化,直至其它峰显示为标准的吸收线型,停止调节PL1.PL1调节过程中,pivot峰型保持不变.
对经过相位校正后的谱图,单击自动积分按钮,则出现谱图的积分;单击自动寻峰按钮,则出现自动寻找到的谱峰及其化学位移.
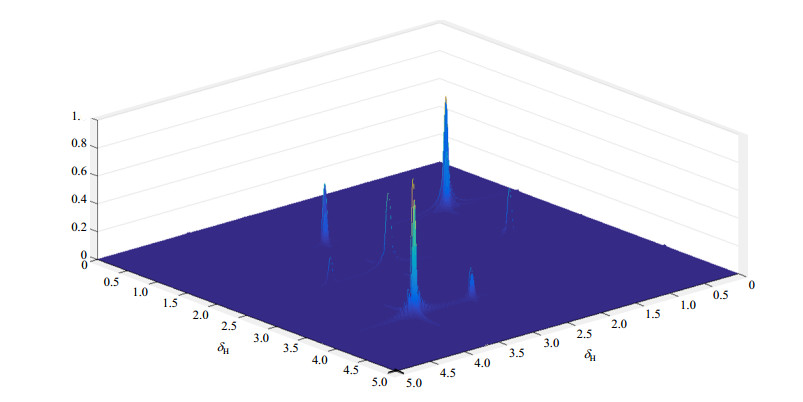
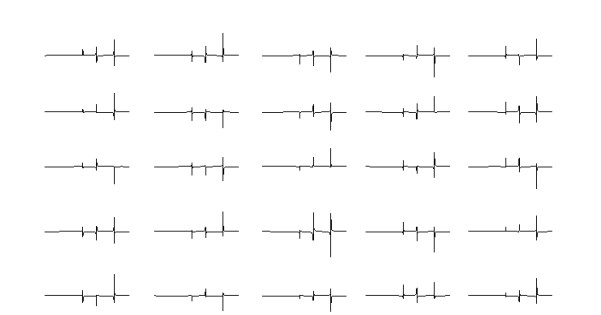
2.3.2 2D NMR谱图采集模拟和数据处理以乙醇样品2D COSY谱采集模拟为例:从软件菜单栏里选择2D Homo序列,进行数据采集,数据总条数为num_t1(固定为100条).采集完成后,进行FT即可得到二维谱图,以堆积圈(mesh)格式(图 7)显示.还可以显示每条t1维数据的FT结果,以观察到不同峰的相位变化(图 8).
|
图 7 VMRS1.0模拟采集虚拟乙醇样品的堆积圈格式的COSY谱 Fig. 7 COSY spectrum showed in mesh style of virtual ethanol sample acquired by VMRS1.0 |
|
图 8 COSY谱(图 7中显示)的前25条数据傅里叶变换后的谱图实部,可观察到不同峰的相位变化 Fig. 8 The real parts of the former 25 1D spectra in COSY experiment (showed in Fig. 7), which showed the phase change of the signals |
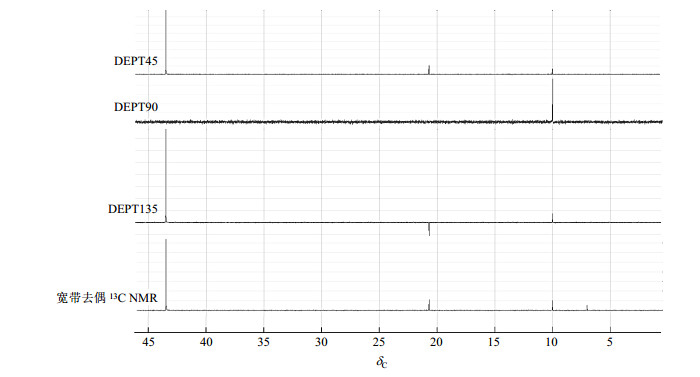
选择DEPT脉冲序列,设置mult分别为0.5、1、1.5,表示设置DEPT序列去偶通道(H通道)第三个脉冲的角度分别为45˚、90˚和135˚,原始数据FT后经过相位校正可以获得不同的13C NMR谱图,结合宽带去偶的13C NMR谱图,可识别伯碳、仲碳、叔碳和季碳.图 9自下而上分别为异辛烷[C8H18,分子式为(CH3)3CCH(CH3)CH2CH3]宽带去偶的13C NMR谱、DEPT135、DEPT90和DEPT45谱图.宽带去偶13C NMR谱显示了所有的13C NMR信号,且均为正峰;DEPT135谱中,伯碳和叔碳信号为正峰,仲碳信号为负峰;DEPT90谱中,只有叔碳信号,且为正峰;DEPT45谱中含伯碳、仲碳和叔碳信号,均为正峰.
|
图 9 利用VMRS1.0模拟采集虚拟异辛烷样品的宽带去偶13C NMR谱和DEPT谱 Fig. 9 The decoupled 13C NMR and DEPT spectra of virtual isooctane sample acquired by VMRS1.0 |
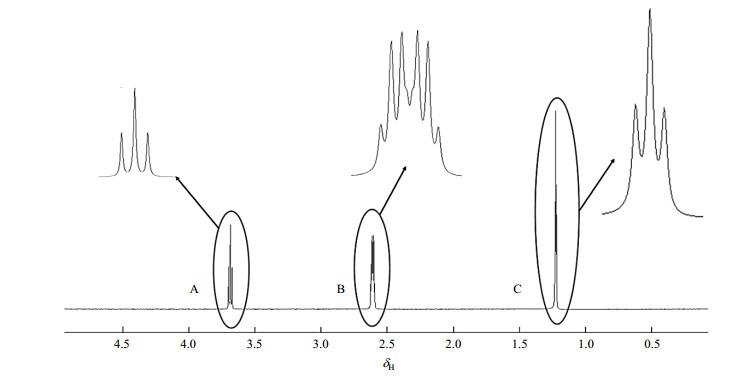
如图 10所示,选择乙醇(CH3CH2OH,内标TMS)作为虚拟样品完成1H NMR谱图的采集模拟,依次进行FT、相位校正、基线校正和积分后,可以得到每个峰族(A、B、C)的积分面积,根据A、B、C积分面积的比值(0.17:0.36:0.47≈1:2:3),以确定分子中处于不同化学环境的原子核的数量之比;分别测量每个峰族的中心频率对应的化学位移(分别为δH 3.69、δH 2.61和δH 1.22),可以推测含有-OH、-CH2、-CH3化学基团;将峰族展宽以后,根据裂分数目可以确定受自旋核影响的数目;根据裂分峰的频率差,可以分析得出不同化学环境核之间的J偶合常数.比如A峰为三重峰,根据裂分数为与之有J偶合作用自旋核数量加1的关系,推断其受周围两个自旋核影响,测量相邻峰之间的频率差为7.97 Hz,可得到A与B之间存在相互偶合作用,且其J偶合系数为7.97 Hz.C峰为三重峰,可知受两个自旋核影响,测量相邻峰之间的频率差为3.25 Hz,可得到C与B之间存在相互偶合作用,其J偶合系数为3.25 Hz.B峰为八重峰,根据8=2×4=(1+1)×(3+1),可知受两种自旋核(数目分别为1和3)的影响,测量相邻峰之间的频率差为7.97 Hz和3.25 Hz,可得到B与A、C之间均存在相互偶合作用,其J偶合系数为7.97 Hz和3.25 Hz.通过上述信息,可以完成乙醇的谱图归属,A、B和C分别对应-OH、-CH2和-CH3基团.
|
图 10 利用VMRS1.0模拟采集的虚拟乙醇样品的1H NMR谱图解析 Fig. 10 The 1H NMR spectrum analysis of virtual ethanol sample acquired by VMRS1.0 |
本文开发的仿真NMR波谱仪VMRS1.0不受制于硬件,可用于相关领域学生和从业人员的低成本、批量化的实验教学和实践培训,助其理解和掌握NMR基本原理和实验操作,了解数据采集参数和波谱处理过程对样品NMR谱图的影响规律,进而提高NMR谱图解析能力.VMRS1.0软件还可用于仪器开发和测试校准.真实NMR波谱仪器受到众多的因素影响,比如电子学噪声、涡流、系统死时间等,导致无法评价最终获得的谱图是否受到设备硬件的影响,还是真实反应了样品的特性.应用VMRS1.0软件,可将标准样品在理想硬件条件获得的谱图作为测试标准,从而作为硬件评价指标.
但VMRS1.0软件在分子样品的信息模型构建方面还有待完善,目前主要针对的是小分子模型,分子信息量相对较少、建模相对简单、分子信息库的数据字段也不高,对于信息存储和数据的模拟采集压力不大.后期需要构建更为复杂的分子信息模型,而且在尽量降低模拟数据采集数据量的情况下完成分子信息数据库构建.另外,对于13C NMR谱,目前只能按照伯、仲、叔、季四种碳来建模,所有伯碳的化学位移都认为是相同的,但它们实际上是有差异的.而且本研究目前只考虑了一键C-H偶合,二键、三键以及更远程C-H偶合信息没有涉及.
| [1] | GUNTER P, SCHAEFER N, OTTING G, et al. POMA:a complete mathematica implementation of the NMR product operator formalism[J]. J Magn Reson A, 1993, 101(4): 103-105. |
| [2] | SMITH S A, LEVANTE T O, MEIER B H, et al. Computer simulations in magnetic resonance:an object-oriented programming approach[J]. J Magn Reson A, 1994, 106(1): 75-105. |
| [3] | ALLMAN T, BAIN A D, GARBOW J R. SIMPLTN:a program for the simulation of pulse NMR spectra[J]. J Magn Reson A, 1996, 123(1): 26-31. |
| [4] | JERSCHOW A, MULLER N. Efficient simulation of coherence transfer pathway selection by phase cycling and pulsed field gradients in NMR[J]. J Magn Reson, 1998, 134(1): 17-29. |
| [5] | MERSI G H, CUPERLOVIC M, PALKE W E, et al. Pulsed field gradients in simulations of one-and two-dimensional NMR spectra[J]. J Magn Reson, 1999, 137(1): 186-195. |
| [6] | JIN F Z, CHEN H W, ZHOU R X, et al. Experimental simulation of the Unruh effect on an nuclear magnetic resonance (NMR) quantum simulator[J]. Science China:Physics, Mechanics and Astronomy, 2016, 59(3): 1-8. |
| [7] | TOSNER Z, ANDERSON R, STEVENSON B. SIMPSON:A general program for solid-state NMR spectroscopy[J]. J Magn Reson, 2000, 147(2): 296-330. |
| [8] | SCHATS P. NMR Simulator[J]. J Chem Edu, 1988, 65(4): 296-297. |
| [9] | NICOLAS P, FUSHMAN D, RUCHINSKY V, et al. The virtual NMR spectrometer:a computer program for efficient simulation of NMR experiments involving pulsed field gradients[J]. J Magn Reson, 2000, 145(2): 262-275. |
| [10] | KEELER J. Understanding NMR spectroscopy[M]. London: Wiley, 2002: 80-118. |
 2019, Vol. 36
2019, Vol. 36 
