阿尔茨海默病是一种神经系统退行性疾病[1, 2],主要症状为记忆力减退和认知功能下降[3],发病过程存在三种状态[4]:健康人体(认知功能正常,Cognitive Normal,CN)、轻度认知障碍(Mild Cognitive Impairment,MCI)、阿尔茨海默病症(Alzheimer Disease,AD),对其病程早期分类诊断至关重要.
目前利用三维脑部磁共振图像特征进行阿尔茨海默病程分类诊断的研究[5-8]多采用图像的整体特征,如采用灰度共生矩阵[5]和游程长矩阵[6, 7]提取纹理参数,或者测量感兴趣区域体积的变化量[8].但由于阿尔茨海默病三种状态下各感兴趣组织的萎缩程度不同,而且在疾病早期,部分组织的萎缩程度不太明显,纹理排列变化不大,所以图像整体特征不能充分反映病灶的特征变化和患者的个体差异.
局部模式变换纹理特征[9]可以反映组织局部的相对强度差异;而灰度共生、灰度游程、灰度区域大小及局部灰度差分矩阵类产生的特征[10, 11]是常见的常规整体纹理特征,可以反映图像的亮度分布特性和具有相同亮度的像素的位置分布信息.两类特征之间存在互补性,将两者融合可以提高诊断的准确度.本文提出将改进后的三维局部模式变换纹理特征与常规整体纹理特征进行融合的方法,并利用支持向量机分类算法[12]探索其对阿尔茨海默病病程的三个阶段进行分类预测的可能性.
1 数据与方法 1.1 图像数据本研究所使用的磁共振图像样本,包括25例AD患者、61例MCI患者以及46例CN人体的三维全脑磁共振图像和双侧海马体组织的金标准掩模(mask)图像,来自第九届中国大学生服务外包创新创业大赛A22华为命题赛题(人脑核磁共振影像海马体结构检测与分割),数据来自美国ADNI(Alzheimer's Disease Neuroimaging Initiative)中心数据库,其统计特征如表 1所示.
| 表 1 本文所使用的磁共振图像样本的统计 Table 1 Statistical characteristics of the magnetic resonance images used in this research |
本文首先利用来自加州大学洛杉矶分校人体神经影像中心开发的统计参数图(Statistical Parametric Mapping,SPM)——SPM12工具箱[13]对三维全脑磁共振图像进行分割得到灰质和白质;利用双侧海马体组织的金标准mask图像,将其与三维全脑磁共振图像对应体素相乘得到海马体.总共获得三个感兴趣区域:双侧海马体、灰质和白质.然后分别从三个感兴趣区域中提取三维局部模式变换纹理特征和灰度共生类等的常规特征,分别利用支持向量机分类算法对阿尔茨海默病病程的三个阶段进行分类预测.将两类特征融合,再次采用支持向量机分类算法对上述三个阶段进行分类预测.本文的研究设计流程如图 1所示.
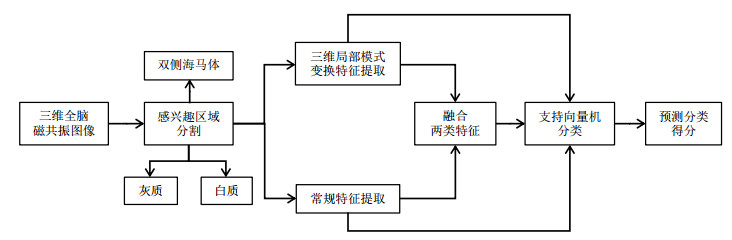
|
图 1 本文设计的阿尔茨海默病病程分类预测流程图 Fig. 1 Flow chart of the course of Alzheimer's disease classification prediction in this research |
在Matlab环境中使用SPM12工具箱从一名AD患者全脑磁共振图像中分割的感兴趣区域的灰质组织和白质组织如图 2所示.
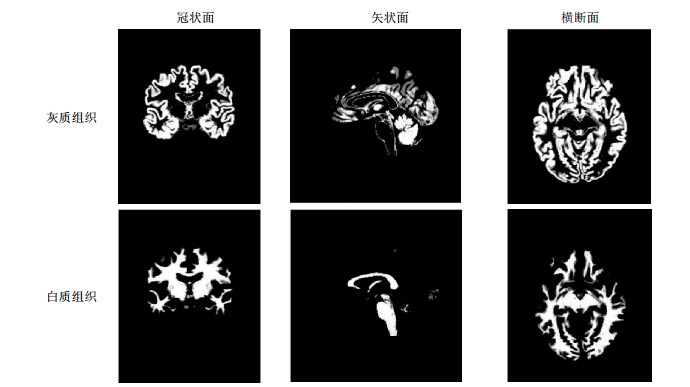
|
图 2 利用统计参数图(SPM)工具箱分割AD患者的灰质组织和白质组织(从左到右依次为:冠状面、矢状面、横断面)
Fig. 2 Splitting gray matter and white matter (from left to right: coronal, sagittal, and cross-section) from the brain MR image of an AD patient with SPM
|
本文首先从磁共振图像的感兴趣区域提取常规特征,包括均值、标准差、偏度和峰度等灰度统计特征参数;从灰度共生矩阵提取能量、对比度和熵等纹理特征参数;从灰度游程矩阵提取短游程因子、长游程因子和灰度不均匀度等纹理特征参数;从灰度区域大小矩阵提取小区域因子、大区域因子和灰度不均匀度等纹理特征参数;从局部灰度差分矩阵提取粗糙度、频度、复杂度和纹理强度等纹理特征参数.
局部模式变换是常用的局部纹理特征提取方法,包括局部二值模式(Local Binary Pattern,LBP)和局部三值模式(Local Ternary Pattern,LTP),计算图像中各邻域的两种局部模式变换值作为局部纹理特征参数,分别统计各模式变换值出现的次数,得出相应的直方图特征向量.
LBP算法最早由Ojala等[14]提出用于构建中心像素点与其周围像素点间的关系.经典LBP算法定义对图像中的像素构造一个3*3邻域,比较以其为中心像素值与邻域像素值的大小关系,将邻域像素值表示成一串八位二进制代码.具体计算流程为:将图像中的每一个像素Ic作为中心像素,选取与Ic邻接的8邻域像素,取顺时针方向(或逆时针方向)将各邻域像素记为I0、I1、…、I7,把Ic点像素值作为比较的阈值.若Ii(i=0, 1, 2, 3, 4, 5, 6, 7)点的像素值比Ic小,则Ii(i=0, 1, 2, 3, 4, 5, 6, 7)二值化为0;否则为1.最后将邻域像素二值化得到的0和1序列看作一串8位二进制代码,将该二进制代码进行十进制转换得到Ic中心点处的LBP值.可用(1)式和(2)式表示:
| $ LB{P_{\rm{8}}} = \sum\limits_{i = 0}^7 {s({I_i}} - {I_c}){2^i} $ | (1) |
| $s(x) = \left\{ \begin{gathered} 1{\rm{ }}x \geqslant 0 \\ 0{\rm{ }}x < 0 \\ \end{gathered} \right. $ | (2) |
其中s表示一种函数映射关系,也可用任意字母表示,即当自变量小于0时,
LTP在LBP的基础上发展而来,最初由Tan等[15]提出,LTP相比LBP引入一个阈值t,具体计算流程为:以图像中的每一个像素Ic为中心像素,选取与Ic邻接的8邻域点,按照顺时针方向(或逆时针方向)将各邻域像素记为I0、I1、…、I7,自定义阈值或设计自适应阈值算法确定阈值t.如果Ii(i=0, 1, 2, 3, 4, 5, 6, 7)点的像素值与Ic点处像素值之差大于等于阈值t,则Ii点像素值三值化为1;如果Ii(i=0, 1, 2, 3, 4, 5, 6, 7)点的像素值与Ic点像素值之差小于等于阈值t的负值,则三值化为-1;否则为0.可用(3)式表示:
| $s'({I_i},{I_c},t) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;{I_i} - {I_c} \ge t\\ 0\;\;\;\;\;\;{\rm{|}}{I_i} - {I_c}|\,<t\\ - 1\;\;\;\;{I_i} - {I_c} \le - t \end{array} \right.$ | (3) |
其中
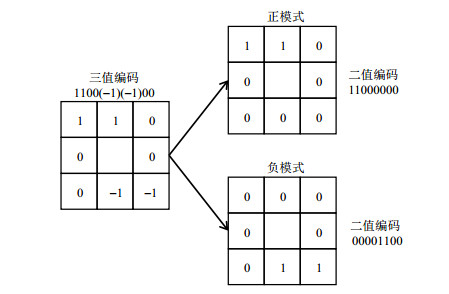
|
图 3 正模式和负模式局部二值化处理的局部三值模式 Fig. 3 LTP values divided into positive mode LBP and negative mode LBP |
本文将LBP和LTP推广到三维图像中,提出改进的三维局部模式变换以提取图像的纹理特征,在三维图像中进行采样要比在二维图像中复杂,需要考虑三维空间中采样顺序及采样数据量过大的问题.既往研究[16-18]的三维局部模式变换多使用整体三维图像的三个正交特征面来提取特征,但考虑到三维图像中的体素块,且增加特征平面可以更充分的反映三维图像中各组织的结构等相关信息,所以本文提出利用一个3*3*3体素模板的采样模型在三维图像体素块的9个特征方向上进行两种局部模式变换来提取纹理特征,具体的计算步骤如下:
(1)确定一个3*3*3=27个体素的三维邻域采样模型;
(2)从该采样邻域模型中选取过该采样中心9个方向上的平面作为进行局部模式变换的特征平面.其中,与坐标轴正交的特征平面有3个,在每个与坐标轴正交的特征平面方向上都对应有2个与坐标轴方向夹角成45°的斜向特征平面,如图 4所示;
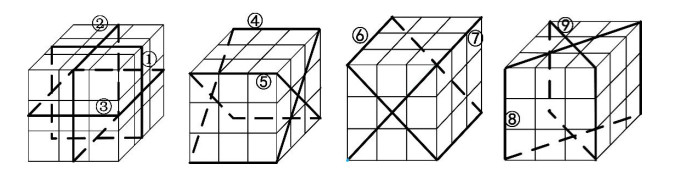
|
图 4 本文提出的三维局部模式变换的9个特征平面 Fig. 4 Nine feature planes of 3D local mode transformation proposed in this research |
(3)用3*3*3体素模板矩阵的三维邻域采样模型依次对图像的体素块进行迭代,直至历经图像所有的体素,每次迭代都计算9个方向特征平面的两种局部模式变换特征;
(4)对计算得到的局部模式变换特征图谱统计局部模式值出现的次数,并将其标准化到0和1之间,即得到特征图谱的直方图特征向量.
1.2.3 三维纹理特征融合三维局部模式变换特征提取得到的实则为直方图特征向量.
对于简单的LBP和LTP,对二维图像变换提取特征可得到256(取值范围:0~255)个LBP值或LTP值,则9个特征平面可得到256*9=2 304维特征向量.常规特征包括从各个矩阵中得出的纹理特征参数以及偏度,峰度等灰度统计特征,获得43维特征向量.两者简单融合可得到2 304+43=2 347维特征向量.
而对于旋转不变和uniform模式的LBP和LTP,对二维图像变换提取特征可得到60(取值范围:0~59)个LBP值或LTP值,则9个特征平面可得到60*9=540维特征向量,将其与常规特征简单融合可得到540+43=583维特征向量.
1.2.4 特征分类预测本文采用Weka软件[19]集成的支持向量机(Support Vector Machine,SVM)分类算法对阿尔茨海默病程进行分类预测.SVM是机器学习中分类常用的工具之一[20].本文首先分别对基于三维局部模式变换及常规方法提取的特征应用SVM进行分类,得到预测分类结果;然后对融合后的特征再次应用SVM进行分类,得到预测分类结果;最后采用十折交叉验证法[21]对SVM分类性能进行验证,并利用预测分类的受试者工作特征曲线(Receiver Operating Characteristic Curve,ROC)曲线下面积(Area Under the Curve,AUC)、准确率、敏感度和特异度指标评估分类性能.
2 实验结果与讨论我们首先采用SVM算法评估了各个感兴趣组织利用基于改进三维局部模式变换纹理特征、灰度共生类常规特征,以及两者融合纹理特征三类方法预测阿尔茨海默病病程分类的准确率、敏感度、特异度(表 2~5和图 5).然后绘制了各个感兴趣组织采用上述三类方法预测AD组和CN组分类的ROC曲线(图 6),并将本文方法(基于改进三维局部模式变换的纹理特征融合常规特征)所得的基于海马体磁共振图像的AD组和CN组分类预测的ROC曲线与传统方法(文献[16]:对整幅图像仅采用3个特征平面的局部模式变换;文献[17]:对合成三通道图像仅采用5个特征平面的局部模式变换)进行了比较(图 7).
| 表 2 利用支持向量机(SVM)算法对基于海马体磁共振图像采用3种纹理特征提取方法进行阿尔茨海默病病程分类预测的准确率、敏感度、特异度评估 Table 2 Accuracy, sensitivity and specificity evaluation for Alzheimer's disease classification prediction using SVM algorithm based on hippocampal magnetic resonance images treated with 3 texture feature extraction methods |
| 表 3 利用支持向量机(SVM)算法对基于灰质磁共振图像采用3种纹理特征提取方法进行阿尔茨海默病病程分类预测的准确率、敏感度、特异度评估 Table 3 Accuracy, sensitivity and specificity evaluation for Alzheimer's disease classification prediction using SVM algorithm based on gray matter magnetic resonance images treated with 3 texture feature extraction methods |
| 表 4 利用支持向量机(SVM)算法对基于白质磁共振图像采用3种纹理特征提取方法进行阿尔茨海默病病程分类预测的准确率、敏感度、特异度评估 Table 4 Accuracy, sensitivity and specificity evaluation for Alzheimer's disease classification prediction using SVM algorithm based on white matter magnetic resonance images treated with 3 texture feature extraction methods |
| 表 5 利用支持向量机(SVM)算法对基于结合灰质和白质磁共振图像采用3种纹理特征提取方法进行阿尔茨海默病病程分类预测的准确率、敏感度、特异度评估 Table 5 Accuracy, sensitivity and specificity evaluation for Alzheimer's disease classification prediction using SVM algorithm based on combined gray matter and white matter magnetic resonance images treated with 3 texture feature extraction methods |
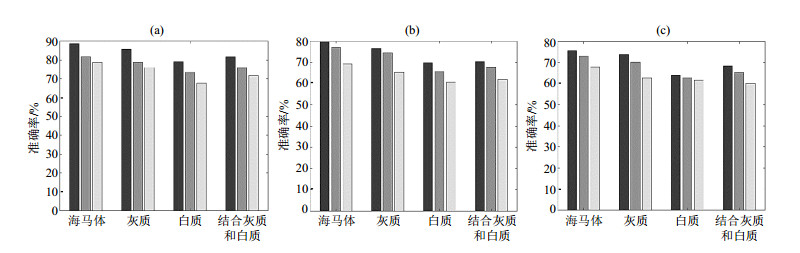
|
图 5 利用支持向量机(SVM)算法对基于不同感兴趣组织磁共振图像采用3种纹理特征提取方法(黑色:融合纹理特征;深灰:改进三维局部模式变换纹理特征;浅灰:灰度共生类常规特征)进行阿尔茨海默病病程分类预测的准确率评估. (a) AD vs. CN; (b) MCI vs. CN; (c) AD vs. MCI Fig. 5 Accuracy evaluation for Alzheimer's disease classification prediction using SVM algorithm based on different regions of interested magnetic resonance images treated with 3 texture feature extraction methods (black: Fusion texture features; deep gray: Improved 3D local pattern transform texture features; light gray: General features of gray level co-occurrence). (a) AD vs. CN; (b) MCI vs. CN; (c) AD vs. MCI |

|
图 6 基于不同感兴趣组织磁共振图像采用3种纹理特征提取方法进行AD组和CN组分类预测的ROC曲线. (a) 白质;(b) 灰质;(c) 海马体;(d) 结合灰质和白质 Fig. 6 ROC curves for AD group and CN group classification prediction based on magnetic resonance images different regions of interested treated with 3 texture feature extraction methods. (a) White matter; (b) Gray of matter; (c) Hippocampus; (d) Combining gray matter and white matter |

|
图 7 本文方法与文献方法所得的基于海马体磁共振图像的AD组和CN组分类预测的ROC曲线 Fig. 7 ROC curves for AD group and CN group classification prediction based on hippocampal magnetic resonance images treated with the proposed method in this research and reference method |
由上述图表可知基于海马体磁共振图像利用改进的三维局部模式变换纹理特征方法对CN组和AD组进行分类预测的准确率为81.69%、敏感度为76.00%、特异度为93.50%,AUC为0.816 5;基于灰质磁共振图像准确率为78.87%,敏感度为72.00%、特异度为82.60%、AUC为0.782 1;基于白质磁共振图像的准确率为73.42%、敏感度为64.00%、特异度为76.10%、AUC为0.731 3;基于灰质和白质结合的磁共振图像的准确率为76.06%、敏感度为70.00%、特异度为80.32%、AUC为0.759 8. 利用改进的三维局部模式变换纹理特征与常规特征融合的方法基于海马体磁共振图像对CN组和AD组进行分类预测的准确率达到88.73%、敏感度为78.00%、特异度为95.70%、AUC为0.886 5;基于灰质磁共振图像的准确率达到85.92%、敏感度为80.00%、特异度为86.60%、AUC为0.854 3;基于白质磁共振图的准确率达到79.06%、敏感度为65.20%、特异度为82.60%,AUC为0.789 6;基于灰质和白质结合的磁共振图像的准确率达到81.69%、敏感度为75.30%、特异度为85.00%、AUC为0.812 3.可见无论是基于利用改进三维局部模式变换纹理特征的方法,还是其与灰度共生类常规特征融合的融合纹理特征方法,在基于海马体磁共振图像时对于AD组与CN组的分类预测效果最好,在基于灰质磁共振图像时的效果较好,而在基于白质磁共振图像时的效果不是很显著;由于白质特征在早期的变化不明显,综合利用灰质和白质磁共振图像特征后,白质的特征可能会对分类效果造成干扰,导致准确率反而有所下降.
同样地也可以看到无论是基于海马体磁共振图像,还是基于灰质磁共振图像,又或者是基于白质磁共振图像,也无论是对于AD组与CN组,MCI组与CN组或AD组与MCI组,利用融合纹理特征进行分类预测的效果最好,单独使用改进三维局部模式变换纹理特征进行分类预测的效果较好,而单独使用常规特征的分类效果不是很显著.
由表 2~5还可知,无论是基于何种感兴趣组织,三种方法对于AD组与CN组分类预测的性能要远优于MCI组与CN组、AD组与MCI组.因此本文对另外两个组分类预测的结果不多加讨论.
由图 7可知,相对于文献[16]和文献[17]提出的一般三维局部模式变换方法,利用本文基于改进三维局部模式变换的纹理特征融合常规特征的方法在基于海马体磁共振图像对AD组和CN组进行分类预测时,效果更好,AUC达到0.886 5.
本研究的创新之处在于:(1)与传统的基于图像二维特征进行阿尔茨海默病病程分类诊断模型相比,本文采用改进的三维局部模式变换特征提取方法利用了三维图像更丰富的内在结构信息来帮助分类诊断;(2)既往研究虽然提出三维局部模式变换,但大多实则所使用的只是三维图像的三个正交特征平面,而本文通过对三维图像的每一个体素块使用9个方向上的特征平面提取纹理信息;(3)目前研究者们大多通过单一的特征提取方法得到图像特征来对图像进行分类,本文提出将局部模式变换提取的特征与常规特征进行融合对阿尔茨海默病病程分类诊断,由于阿尔茨海默病病程三个阶段中各个感兴趣组织区域的萎缩程度不相同,所以组织的纹理排列顺序也不同,局部纹理特征之间存在的差异较大,应用三维局部模式变换可以反映三种状态下各个组织局部纹理之间的强度差,与灰度共生、灰度游程、灰度区域大小和局部灰度差分矩阵类常规特征反映出图像灰度分布信息具有互补性,能够提取出更加有价值的特征信息,提高预测分类的精度.
本研究的不足之处在于:(1)实验样本量较小,且阿尔茨海默病病程三个阶段的实验样本量不均匀;(2)只采用三个感兴趣区域的组织.在往后的研究中,需要加大实验对象的样本;基于分割算法[22, 23]对全脑磁共振图像进行分割得到多个感兴趣区域的组织,如胼胝体、杏仁核等,进一步提高阿尔茨海默病早期诊断分类的鲁棒性.
3 结论(1)相比单独使用一种特征,将局部模式变换与灰度共生矩阵、灰度游程矩阵、灰度区域大小矩阵和局部灰度差分矩阵的纹理特征提取方法相结合用于双侧海马体组织可以明显提高阿尔茨海默病的分类诊断准确率;(2)在双侧海马体组织应用三维纹理特征提取方法进行阿尔茨海默病早期诊断的准确率要高于其他组织;(3)使用本文方法对AD组与CN组分类预测的准确率最高,MCI组与CN组分类预测的准确率次之;(4)利用改进的三维局部模式变换提取的纹理特征,并与常规特征进行融合,可以提供更全面的信息,提高阿尔茨海默病病程分类预测的准确度,为阿尔茨海默病的早期诊断提供有效的参考价值.
| [1] | SAMI S, WILLIAMS N, HUGHES L E, et al. Neurophysiological signatures of Alzheimer's disease and frontotemporal lobar degeneration:pathology versus phenotype[J]. Brain, 2018, 141(8): 2500-2510. DOI: 10.1093/brain/awy180. |
| [2] | KIM H, LEE J U, SONG S, et al. A shape-code nanoplasmonic biosensor for multiplex detection of Alzheimer's disease biomarkers[J]. Biosens Bioelectron, 2018, 101: 96-102. DOI: 10.1016/j.bios.2017.10.018. |
| [3] | ALZHEIMEI'S ASSOCIATION. 2018 Alzheimer's disease facts and figures[OL]. http://www.alz.org/alzheimers-dementia/facts-figures. |
| [4] | ZHANG Y D, WANG S H, PHILLIPS P, et al. Detection of Alzheimer's disease and mild cognitive impairment based on structural volumetric MR images using 3D-DWT and WTA-KSVM trained by PSOTVAC[J]. Biomed Signal Proces, 2015, 21: 58-73. DOI: 10.1016/j.bspc.2015.05.014. |
| [5] |
XIA H, LIU W F, WANG X, et al. Comparative study of two-dimensional and three-dimensional texture analysis of brain MR images in patients with Alzheimer's disease[J].
Journal of Beihua University (Nature), 2013, 14(5): 553-556.
夏翃, 刘卫芳, 王旭, 等. 阿尔茨海默病患者脑MR图像二维及三维纹理分析比较研究[J]. 北华大学学报(自然), 2013, 14(5): 553-556. |
| [6] |
LI X, TONG L Z, ZHOU X X, et al. Classification of Alzheimer's disease and mild cognitive impairment based on three-dimensional texture features of MR images[J].
Chinese Medical Imaging Technology, 2011, 27(5): 1047-1051.
李昕, 童隆正, 周晓霞, 等. 基于MR图像三维纹理特征的阿尔茨海默病和轻度认知障碍的分类[J]. 中国医学影像技术, 2011, 27(5): 1047-1051. |
| [7] |
YU L, XIA H, LIU W F. Classification of Alzheimer's disease and healthy controls based on three-dimensional texture features of hippocampus based on magnetic resonance images[J].
Journal of Biomedical Engineering, 2016(6): 1090-1094.
于鲁, 夏翃, 刘卫芳. 基于磁共振图像海马三维纹理特征的阿尔茨海默病及健康对照的分类研究[J]. 生物医学工程学杂志, 2016(6): 1090-1094. |
| [8] | JONGKREANGKRAI C, VICHIANIN Y, TOCHAROENCHAI C, et al. Computer-aided classification of Alzheimer's disease based on support vector machine with combination of cerebral image features in MRI[J]. Journal of Physics:Conference Series, 2016, 694(1): 012036. |
| [9] | JAISWAL A K, BANKA H. Local pattern transformation based feature extraction techniques for classification of epileptic EEG signals[J]. Biomed Signal Proces, 2017, 34: 81-92. DOI: 10.1016/j.bspc.2017.01.005. |
| [10] | HARALICK R M, SHANMUGAM K, DINSTEIN I H. Textural features for image classification[J]. IEEE T Syst Man Cy, 1973, smc-3(6): 610-621. DOI: 10.1109/TSMC.1973.4309314. |
| [11] | THIBAULT G, ANGULO J, MEYER F. Advanced statistical matrices for texture characterization: Application to DNA chromatin and microtubule network classification[C]//IEEE International Conference on Image Processing. 2011. |
| [12] | JOACHIMS T. Making large-scale SVM learning practical[R]//Technische Universität Dortmund, Sonderforschungsbereich 475: Komplexitätsreduktion in Multivariaten Datenstrukturen, 1998. |
| [13] |
ZHANG H M, CHEN S Z. A new brain function imaging analysis method-Statistical parametric mapping(SPM)[J].
Chinese Medical Imaging Technology, 2002, 18(7): 711-713.
张海敏, 陈盛祖. 一种新的脑功能显像分析法-统计参数图(SPM)[J]. 中国医学影像技术, 2002, 18(7): 711-713. DOI: 10.3321/j.issn:1003-3289.2002.07.038. |
| [14] | OJALA T, PIETIKÄINEN M, MÄENPÄÄ T. Gray scale and rotation invariant texture classification with local binary patterns[C]//European Conference on Computer Vision. Springer, Berlin, Heidelberg, 2000. |
| [15] | TAN X Y, TRIGGS B. Enhanced local texture feature sets for face recognition under difficult lighting conditions[J]. IEEE Trans Image Process, 2010, 19(6): 1635-1650. DOI: 10.1109/TIP.2010.2042645. |
| [16] | LI M W, OISHI K, HE X H, et al. An efficient approach for differentiating Alzheimer's disease from normal elderly based on multicenter MRI using gray-level invariant features[J]. PloS One, 2014, 9(8): e105563. DOI: 10.1371/journal.pone.0105563. |
| [17] | MURALA S, WU Q M J. Spherical symmetric 3D local ternary patterns for natural, texture and biomedical image indexing and retrieval[J]. Neurocomputing, 2015, 149: 1502-1514. DOI: 10.1016/j.neucom.2014.08.042. |
| [18] | MORGADO P, SILVEIRA M, MARQUES J S. Diagnosis of Alzheimer's disease using 3D local binary patterns[J]. Computer Methods in Biomechanics & Biomedical Engineering Imaging & Visualization, 2013, 1(1): 2-12. |
| [19] | HOLMES G, DONKIN A, WITTEN I H. WEKA: a machine learning workbench[C]//Brisbane: Proceedings of ANZⅡS'94-Australian New Zealand Intelligent Information Systems Conference, 1994. doi: 10.1109/ANZⅡS.1994.396988. |
| [20] | ALTAF M A B, TILLAK J, KIFLE Y, et al. A 1.83µJ/classification nonlinear support-vector-machine-based patient-specific seizure classification SoC[C]//IEEE International Solid-State Circuits Conference Digest of Technical Papers. 2013: 100-101. |
| [21] | CHIK Z, ALJANABI Q A, KASA A, et al. Tenfold cross validation artificial neural network modeling of the settlement behavior of a stone column under a highway embankment[J]. Arab J Geosci, 2014, 7(11): 4877-4887. DOI: 10.1007/s12517-013-1128-6. |
| [22] |
SONG Y, XIE H B, YANG G. Segmented dictionary learning algorithm for compressed perceptual magnetic resonance imaging[J].
Chinese J Magn Reson, 2016, 33(4): 559-569.
宋阳, 谢海滨, 杨光. 用于压缩感知磁共振成像的分割字典学习算法[J]. 波谱学杂志, 2016, 33(4): 559-569. |
| [23] |
ZHU X T, HE X B, LIU Y, et al. Semi-automatic region division and cell counting method for simple brain slice images[J].
Chinese J Magn Reson, 2018, 35(2): 133-140.
朱续涛, 何晓斌, 刘悦, 等. 一种简易的脑片图像的半自动区域划分及细胞计数方法[J]. 波谱学杂志, 2018, 35(2): 133-140. |
 2019, Vol. 36
2019, Vol. 36 
