Liquid crystals, as an important class of material, are produced in large quantities for use in optical displays. The synthesis of novel liquid crystalline compounds and the exploration of potential applications of liquid crystals in other fields remain research active. As most applications of liquid crystals depend on their orientation order, the nematic order parameter is among the most important properties of any new type of liquid crystalline material.
The order parameter, first used by Tsvetkov[1] in the field of liquid crystals and also known as Maier-Saupe order parameter[2, 3], is given by
| $ S=\left(3 \cos ^{2} \theta-1\right) / 2 $ | (1) |
The angle θ denotes the orientation of the axis of a given molecule, considered as a rigid rod, with respect to the average orientation of all molecules, the director. The angular brackets denote the average over the orientation distribution function of all molecules. For perfect order all rods are parallel, that is, θ = 0, resulting in S=1. Real molecules, however, are neither uniaxial nor rigid. Biaxiality is taken care of by introduction of the ordering matrix[3-5]. Its largest principal value Szz corresponds to S and the difference Sxx-Syy of the other two principal values is the biaxiality of the molecule. More detailed models[6-12] are required since molecules are flexible. For each rigid subunit of a molecule, a local order matrix can be defined, and in addition to the orientation of the molecules, their conformational changes must be considered in the averaging process.
Over years, nuclear magnetic resonance (NMR) spectroscopy has proven to be a powerful and versatile technique for obtaining detailed information on the molecular order in liquid crystalline phases[4, 8, 9, 11-30].The advantage of NMR in the determination of order parameters lies in the fact that both the orientation of quadrupolar, dipolar or chemical shift interactions with respect to molecular axes and the reference values corresponding to perfect order are known. Chemical shift tensors can nowadays be obtained from quantum chemical calculations[31]. Therefore, absolute order parameters can be calculated from NMR data. This is different from all methods based on electric properties, such as birefringence[25-27, 32, 33], dielectric anisotropy[25-27, 34, 35], dielectric relaxation[36], ultraviolet (UV)[18], or infrared (IR)[18, 37] absorption dichroism, fluorescence[38] and Raman scattering[39], since the local electric field and thus the orientation of the observed tensorial property with respect to molecular axes is generally not known[32, 35, 37, 40-41]. Although the orientation of local field is known in the case of magnetic properties, determination of order parameters from the anisotropy of diamagnetic susceptibilities[41, 42] seems less common, probably because the required instruments are not always available and diamagnetic susceptibility measurements are less precise than, for example, optical measurements[32].
In order to obtain the reference value for perfect order in the case of electric properties as mentioned above, an extrapolation method first suggested by Haller[32] can be used. The two-parameter equation
| $ S=\left(1-T / T_{\mathrm{NI}}\right)^{\eta} $ | (2) |
where TNI is the nematic-to-isotropic (N-I) phase transition temperature. S=X/X0 is the order parameter obtained from the measured quantity X (e.g., the birefringence), and the fitting parameter X0 is the reference value for perfect order, usually fits the experimental data well. The second fit parameter, the exponent h, is mostly considered as an empirical parameter.
Since the nematic-to-isotropic phase transition is of first order with a discontinuity of S at the phase transition, Equ. (2) is valid only when temperature is sufficiently far below the phase transition
temperature TNI. Therefore, a three-parameter equation
| $ S=\left(1-T / T^{*}\right)^{\eta} $ | (3) |
is suggested. The additional parameter T* can be considered as a temperature slightly above TNI where S becomes 0 at a hypothetical second-order phase transition[32]. In practice, T* is found to be only about 0.1 K higher than TNI [41]. Therefore, the two-parameter fit according to Equ. (2) works well.
Although the Haller Equ. (2) or (3) provide a good approximation of experimental data, the values of η are not consistent with the theories of weakly first-order nematic-to-isotropic phase transition. Therefore, a four-parameter expression for the temperature dependence of S
| $ S=S^{* *}+A\left(1-T / T^{* *}\right)^{\eta} $ | (4) |
has been introduced[33]. Here, T** is the effective second order phase transition temperature and S**=S(T**). For S=1 at T=0, it follows that S**+A=1, which leaves one with the three independent fit parameters η, T** and A. Equ. (4) was shown to reproduce experimental data while at the same time being consistent with theory[33].
Even though lacking a theoretical foundation, the simple two-parameter Haller equation is sufficient to convert experimental data into order parameters in most cases, and will be used here in combination with NMR data. To date, there have been very few examples for the application of the Haller relationship in NMR[20-27]. Its validity for proton-deuterium dipolar couplings and deuterium quadrupole couplings in partially deuteriated 4-n-pentyloxy-4'-cyanobiphenyl (5OCB) has been explored by Heeks and Luckhurst[20]. Siebert[22] found that the Haller relationship showed good agreement with the temperature dependence of deuterium quadrupole couplings for several types of polymeric nematic liquid crystals. Nagaraja et al.[23] observed fairly good agreement with the Haller equation for order parameters obtained from dipolar oscillations in a two-dimensional experiment and from deuterium NMR. Furthermore, order parameters derived from 13C-19F dipolar couplings and anisotropic 13C chemical shifts in fluorinated calamitic nematics were found to be consistent with Haller-type relationships[25-27]. Magnuson et al.[21] derived several functional forms for the temperature dependence of the order parameter from the Landau-de Gennes theory[41] and found that the one which fits experimental order parameters derived from 13C chemical shift data best has the form of the Haller relationship[21]. On the other hand, the temperature dependence of the order parameter of banana-shaped molecules could not be described by the Haller relationship[24].
Quadruple couplings, dipolar couplings of individual spin pairs, and anisotropic chemical shifts provide valuable information to test theoretical models of liquid crystalline order. To obtain the data, however, requires synthetic efforts, advanced experiments and/or complex data analysis. Therefore, simpler methods for obtaining order parameters are generally preferred over NMR. Here we present a facile NMR method for the estimation of order parameters. We applied the Haller relationship to obtain order parameters from one-dimensional proton NMR spectra of fully protonated liquid crystals. Experiment and data analysis are easy, and the method is potentially useful as a routine characterization technique for liquid crystals.
1 Experimental4-cyano-4'-pentylbiphenyl (5CB) and the liquid crystal mixture E7 were obtained from Merck (Darmstadt, Germany). E7 is a nematic mixture, containing 51% 5CB, 25% 4-cyano-4'-heptylbiphenyl (7CB), 16% 4-cyano-4'-octyloxybiphenyl (8OCB), and 8% 4-cyano-4'-pentylterphenyl (5CT). The clearing point of 5CB is 35.32 ℃[33]. The clearing point of E7 is 58 ℃ according to the supplier's safety data sheet. All chemicals were used without further purification.
The samples were filled into 4 mm (outer diameter) magic angle spinning (MAS) rotors for NMR measurements. The proton spectra were recorded at 299.81 MHz on a 300 MHz Tecmag Apollo NMR spectrometer using a Bruker MAS probe at static conditions, following a 90˚ pulse of 3.65 µs. The samples were heated from the nematic phase at room temperature and spectra were recorded throughout the nematic region up to the isotropic phase in intervals of 1 K and 5 K for 5CB and E7, respectively. Close to the nematic-to-isotropic transition, smaller temperature intervals were chosen. The samples were heated by a standard NMR air-flow system, resulting in temperature constant to about ±0.1 K. Due to a temperature gradient between temperature sensor and sample, there is a temperature-dependent deviation between measured temperature and true sample temperature. The sample temperatures were obtained via a linear fit using three calibration points. The calibration points are 25 ℃ (no temperature gradient) and TNI, which are taken as those temperatures at which isotropic peaks first appear in the spectra upon increasing temperature, of 5CB (Tmeasured = 36.9 ℃, 1.58 ℃ higher than literature value[43]) and E7 (Tmeasured = 61.5 ℃, 3.5 ℃ higher than literature value[44]). In the following, temperature values corrected in this way are reported.
2 Results and discussion 2.1 1H NMR spectraNMR spectroscopy can be used to determine the clearing point of liquid crystals because of the large difference between the spectra of nematic and isotropic phases. This can be seen from the temperature-dependent spectra of 5CB and E7, which are depicted in Fig. 1 and Fig. 2, respectively. In the nematic phase, the spectra are very broad due to dipolar couplings between the spins. The spurious sharp peaks observed for 5CB in the nematic phase result from a very small amount of an impurity. The pair-wise dipolar couplings depend on the internuclear distance rij as rij-3 and on the angle θij between the internuclear axis and the magnetic field as (3cos2θij-1)/2. Due to the large number of coupled spins in each molecule there are a huge number of transitions, which are not resolved and give rise to the broad humps observed.
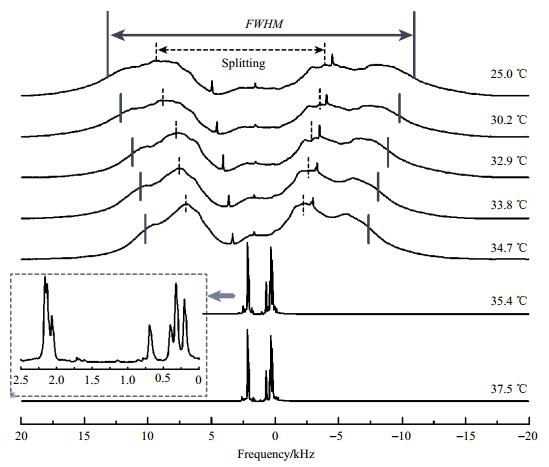
|
Fig. 1 Temperature dependence of the 1H NMR spectra of 5CB. The Splitting or the full width at half maximum (FWHM), as indicated on each spectrum, is used to determine the order parameter. The inset shows an enlargement of a spectrum in the isotropic phase. The calibrated temperatures are given next to the spectra on the right side |
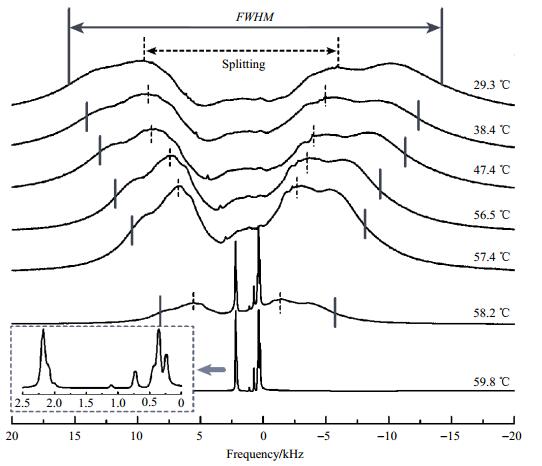
|
Fig. 2 Temperature dependence of the 1H NMR spectra of E7. The Splitting or the full width at half maximum (FWHM), as indicated on each spectrum, is used to determine the order parameter. The inset shows an enlargement of a spectrum in the isotropic phase. The calibrated temperatures are given next to the spectra on the right side |
The total spectrum in the nematic phase resembles one doublet of two very broad lines. This particular line shape proves that the liquid crystal is aligned by the magnetic field. A non-aligned sample would result in a powder pattern consisting, for lack of resolution, of one very broad peak. Because of the positive diamagnetic susceptibility of the aromatic liquid crystal molecules studied, the director is oriented parallel to the magnetic field. The asymmetry of the spectrum is caused by differences in the chemical shifts of the protons.
As temperature increases, the order parameter gets smaller. Therefore, all dipolar couplings and thus the total width of the spectra decrease, as can be seen in Fig. 1 and Fig. 2. In the isotropic phase, the dipolar couplings are averaged to zero because the tumbling motion of the molecules is isotropic. The peaks are narrow and chemical shift differences can be resolved. While 5CB, a one-component system, shows a sharp phase transition, the mixture E7 is biphasic in a temperature range of 1.8 ℃. Since the nematic-to-isotropic phase transition is of first order the two-phase region can be easily identified by the superposition of the two distinct spectra.
2.2 Haller analysisThe dipolar couplings depend on the nematic order parameter S. Because of the large size of the network of coupled spins and the huge number of transitions, it is not possible to extract individual dipolar couplings from the spectrum. A calculation of the spectrum would require the knowledge of the dipolar coupling constants of all proton pairs and the chemical shifts of all protons. However, if chemical shift differences are smaller compared to the dipolar couplings (a condition which is better fulfilled at lower magnetic fields), and if the conformational equilibrium does not depend on temperature, the spectrum is symmetric. Its shape does not depend on temperature, and its width scales with the order parameter S. As can be seen in Fig. 1 and Fig. 2, this is fulfilled in good approximation. Therefore, the overall Splitting as indicated in Fig. 1 and Fig. 2 can be used to estimate the order parameters. Alternatively, the full width at half maximum (FWHM) can be used as a measure of the order parameter. We used the temperature dependence of both parameters, Splitting and FWHM listed in table 1, to fit the data according to the Haller equation [Equ. (2)], setting S=Δν/Δν0, with Δν representing either Splitting or FWHM. The two-parameter fit yields η and the unknown reference value Δν0, which is then used to convert the measured quantity Δν into the order parameter S.
| Table 1 Results of Haller analysis for 5CB and E7 using the range of data points as shown in Fig. 3. The Splitting and FWHM (in kHz) are obtained from Fig. 1 and 2. The corresponding order parameters S of both 5CB and E7 are also plotted in Fig. 4 and 5 |
|
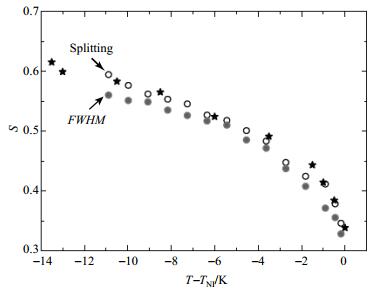
Fig. 4 Nematic order parameter (S) of 5CB as a function of temperature. Open and filled cycles represent the order parameters obtained from Splitting and FWHM, respectively. Stars represent the values taken from Ref. [19] |

|
Fig. 5 Nematic order parameter (S) of E7 as a function of temperature. Open and filled triangles represent the order parameters obtained from Splitting and FWHM, respectively. N and I denote the nematic and isotropic phase, respectively |
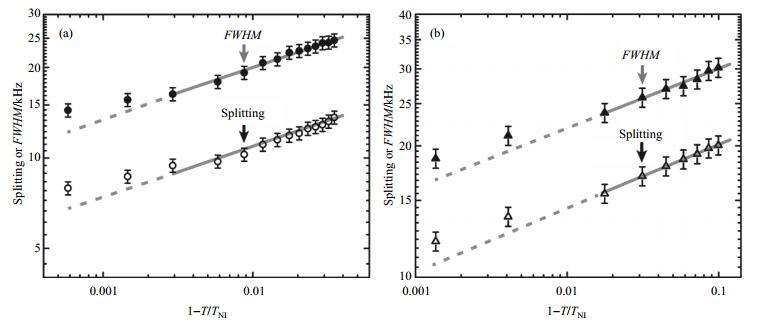
Fig. 3(a) and 3(b) represent the Haller plots for 5CB and E7, respectively. Data points close to the phase transitions were not included in the fit. The parameters Δν0 and η resulting from the fit are listed in Table 1. Including the data points close to the phase transition would result in slightly smaller values for the fit parameters η and Δν0, which produce larger order parameters S.
|
Fig. 3 Haller plots obtained from 1H spectra (shown in Fig. 1 and 2) for the liquid crystals 5CB (a) and E7 (b), respectively. In each figure, the open and the full symbols represent Splitting and FWHM, respectively. Data points close to the phase transition, as indicated by the dashed lines, are not included in the fitting procedure. The error bars correspond to 5% of the data values |
The values of the exponents η, 0.16 and 0.15 (from Splitting) or 0.17 and 0.14 (from FWHM), obtained for 5CB and E7, respectively, are within the range reported in the following literatures for two-parameter Haller fits. As far as Haller fits applied to NMR data are concerned, Heeks and Luckhurst[20] reported an exponent of 0.199 for the 1H-2H dipolar couplings of the hydrogen atoms in ortho position relative to each other on one of the phenyl rings of 4-pentyloxy-4'-cyanobiphenyl (5OCB). Siebert[22] reported Haller exponents for deuterium quadrupole couplings in several liquid crystalline systems. He found η = 0.11 for the nematic solvent 4-n-hexoxy-benzoic acid-(4-tri-deutero-methoxyphenyl-ester) in a solution containing 4 wt.% of the nematic side-chain polymer poly[4-(4-(4-methoxy-phenyl-azo)-phenoxy)-butyl-methacrylate] by fitting the Haller relationship to the quadrupole coupling of the deuteriated methoxy group. For nematic polysiloxanes of the side-chain type with a deuteriated phenyl ring in the 4-methoxy-4'-alkenyloxybenzoate side chain and spacers of different lengths containing 4, 5 or 6 methylene groups (see Ref. [45] for the polymer structure), Siebert obtained exponents between 0.275 and 0.295 when fitting the quadrupole couplings at temperatures sufficiently high for the phenyl rings to rotate freely about their para axes. Finally, a main-chain liquid crystalline polymer with mixed deuteriated alkenyl spacers of different length (dubbed DHMS-7, 9[46]) yielded an exponent of 0.20 according to Siebert[22]. Both our data presented here and all the examples mentioned so far yield linear Haller plots. On the other hand, clear deviations from linearity have been observed by Heeks and Luckhurst[20] in the Haller plots for the deuterium quadrupole couplings of the methylene and methyl groups of the flexible alkoxy chain of 5OCB. These deviations can be explained by a temperature-dependent conformational distribution of the chain and a temperature dependence of the potential of mean torque[20]. Lack of agreement with the Haller relationship was also reported for the temperature dependence of the order parameter Szz associated with the principal axis of the molecular frame of a banana-shaped solute in a calamitic nematic solvent[24]. In this case, a characteristic temperature was introduced as additional parameter to account for the increasing hindrance of the solute motion on lowering the temperature.
Having obtained the reference values Δν0 from the Haller fits, the nematic order parameters S can be calculated as the ratio between the measured Splitting or FWHM, Δν(T), and the fitted parameter Δν0. The order parameters resulting for 5CB and E7 are presented in Fig. 4 and Fig. 5, respectively. In the case of 5CB, the order parameters based on Splittings are slightly higher than those obtained from the analysis of FWHM. Sample values for S are 0.59 (from Splitting) and 0.56 (from FWHM) at 25 ℃(T-TNI=-10.9 in Fig. 4) and 0.35 (from Splitting) and 0.33 (from FWHM) at TNI. The order parameters derived from the Splittings agree better with the order parameters reported by Emsley et al.[19], which describe the orientation of the molecular axis fixed in the phenyl ring carrying the cyano group. Emsley's data are shown in Fig. 4 for comparison. Comparisons of other results for the order parameter of 5CB can be found, for instance, in Fig. 3 of Ref. [34] and in Fig. 1 of Ref. [36].
In the case of E7 (cf. Fig. 5), the Splittings yield slightly lower values than the spectral widths. However, the difference is only about 5 %, similar to 5CB. The difference is of the same order as the experimental errors. As expected, the order parameters of E7 are significantly higher than those of 5CB since the mixture E7 contains longer molecules including a terphenyl derivative. The larger size of the order parameters of E7 is also consistent with a value of 0.7 found by a Raman study of E7[39] and with molecular dynamics simulations of E7 which yielded order parameters up to 0.83[47]. At the phase transition, the order parameter of E7 is also higher than the one of 5CB. The observed temperature dependence of the order parameter within the biphasic regime, which can be seen in Fig. 5, is probably due to a change in the composition of the nematic phase.
3 ConclusionA two-parameter Haller analysis of the spectral Splitting or the FWHM of simple 1H NMR spectra of fully protonated calamitic molecules can be used to obtain reliable estimates of the nematic order parameter as a function of temperature. The Haller relationship holds true if the temperature-dependent equilibrium of different conformers leading to temperature-dependent averages over internal motions has only a small effect on the overall shape of the spectrum. Therefore, we expect the method to work successfully for typical calamitic molecules but suggest some caution before applying it to other types of liquid crystalline molecules. The suggested 1H NMR method does not replace more sophisticated NMR techniques that yield detailed information on order parameters, molecular conformations and dynamics but provides a quick estimate of the order parameter, similar to birefringence measurements. The Haller analysis of proton spectra requires no isotopic labelling, no specialized instrumentation, and no complicated data analysis. So it is easy to use.
Acknowledgement The authors thank Heinz-Siegfried Kitzerow for the liquid crystal samples and for illuminating discussions.| [1] | TSVETKOV V N. Über die molekülanordnung in der anisotrop-flüssigen phase[J]. Acta Physicochim URSS, 1942, 16: 132-147. |
| [2] | MAIER W, SAUPE A. Eine einfache molekular-statistische theorie der nematischen kristallinflüssigen phase[J]. Z Naturforsch A, 1959, 14: 882-889. |
| [3] | ZANNONI C. On the description of ordering in liquid crystals[M]//LUCKHURST G R, VERACINI C A. The molecular dynamics of liquid crystals. Dordrecht: Kluwer, 1994: 11-41. |
| [4] | SAUPE A. Kernresonanzen in kristallinen flüssigkeiten [Nuclear magnetic resonances in crystalline liquids][J]. Z Naturforsch A, 1964, 19: 161-171. DOI: 10.1515/znb-1964-0215. |
| [5] | SAUPE A. Recent results in the field of liquid crystals[J]. Angew Chem Internat Edit, 1968, 7(2): 97-112. DOI: 10.1002/(ISSN)1521-3773. |
| [6] | MARČELJA S. Chain ordering in liquid crystals. Ⅰ. Even-odd effect[J]. J Chem Phys, 1974, 60(9): 3599-3604. DOI: 10.1063/1.1681578. |
| [7] | EMSLEY J W, LUCKHURST G R, STOCKLEY C P. A theory of orientational ordering in uniaxial liquid crystals composed of molecules with alkyl chains[J]. Proc R Soc London A, 1982, 381: 117-138. DOI: 10.1098/rspa.1982.0061. |
| [8] | VAN DER EST A J, KOK M Y, BURNELL E E. Size and shape effects on the orientation of rigid molecules in nematic liquid crystals[J]. Mol Phys, 1987, 60(2): 397-413. DOI: 10.1080/00268978700100271. |
| [9] | JANIK B, SAMULSKI E T, TORIUMI H. Flexible solutes in a uniaxial field: a 2H NMR study of n-alkanes in a nematic solvent[J]. J Phys Chem, 1987, 18(31): 1842-1850. |
| [10] | PHOTINOS D J, SAMULSKI E T, TORIUMI H. Alkyl chains in a nematic field. 1. A treatment of conformer shape[J]. J Phys Chem, 1990, 94(11): 4688-4694. DOI: 10.1021/j100374a058. |
| [11] | GOCHIN M, PINES A, ROSEN M E, et al. Two-dimensional N.M.R. studies of flexible molecules in liquid crystals: orientational order and conformational probabilities of n-hexane[J]. Mol Phys, 1990, 69(4): 671-695. DOI: 10.1080/00268979000100501. |
| [12] | ROSEN M E, RUCKER S P, SCHMIDT C, et al. Two-dimensional proton NMR studies of the conformations and orientations of n-alkanes in a liquid crystal solvent[J]. J Phys Chem, 1993, 97(15): 3858-3866. DOI: 10.1021/j100117a037. |
| [13] | DONG R Y. Nuclear magnetic resonance of liquid crystals[M]. New Jersey: World Scientific, 2010. |
| [14] | COURTIEU J, BAYLE J P, FUNG B M. Variable angle sample spinning NMR in liquid crystals[J]. Prog Nucl Magn Reson Spectrosc, 1994, 26: 141-169. DOI: 10.1016/0079-6565(94)80006-5. |
| [15] | DOMENICI V, GEPPI M, VERACINI C A. NMR in chiral and achiral smectic phases: structure, orientational order and dynamics[J]. Prog Nucl Magn Reson Spectrosc, 2007, 50(1): 1-50. |
| [16] | FUNG B M. 13C NMR studies of liquid crystals[J]. Prog Nucl Magn Reson Spectrosc, 2002, 41(3/4): 171-186. |
| [17] | DOMENICI V. Nuclear magnetic resonance: a powerful tool to study liquid crystals[J]. Liquid Crystals Today, 2017, 26(1): 2-10. DOI: 10.1080/1358314X.2017.1279445. |
| [18] | SAUPE A. Ultraviolet, infrared and magnetic resonance spectroscopy on liquid crystals[J]. Mol Cryst Liq Cryst, 1972, 16(1/2): 87-104. |
| [19] | EMSLEY J W, LUCKHURST G R, STOCKLEY C P. The deuterium and proton-{deuterium} N.M.R. spectra of the partially deuteriated nematic liquid crystal 4-n-pentyl-4'-cyanobipheny[J]. Mol Phys, 1981, 44(3): 565-580. DOI: 10.1080/00268978100102651. |
| [20] | HEEKS S K, LUCKHURST G R. Deuterium nuclear magnetic resonance study of the orientational order in the nematic phase of 4-n-pentyloxy-4'-cyanobiphenyl[J]. J Chem Soc Faraday Trans, 1993, 89(20): 3783-3790. DOI: 10.1039/FT9938903783. |
| [21] | MAGNUSON M L, FUNG B M, BAYLE J P. On the temperature dependence of the order parameter of liquid crystals over a wide nematic range[J]. Liq Cryst, 1995, 19(6): 823-832. DOI: 10.1080/02678299508031106. |
| [22] | SIEBERT H. Untersuchung des Fließverhaltens von flüssigkristallinen polymeren unter Scherung mit 2H-NMR-spektroskopie, Röntgenbeugung, neutronenstreuung und polarisationsmikroskopie [Investigation of the flow properties of liquid-crystalline polymers under shear by 2H NMR spectroscopy, x-ray scattering, neutron scattering and polarizing microscopy][D]. Freiburg: University of Freiburg, 1999. |
| [23] | NAGARAJA C S, RAMANATHAN K V. Determination of order parameters of liquid crystals: use of dipolar oscillations enhanced by Lee-Goldburg decoupling[J]. Liq Cryst, 1999, 26(1): 17-21. DOI: 10.1080/026782999205489. |
| [24] | CINACCHI G, DOMENICI V. Orientational odering of a banana-shaped solute molecule in a nematic calamitic solvent by 2H-NMR-spectroscopy: an indication of glasslike behavior[J]. Phys Rev E, 2006, 74(3 Pt 1): 030701. |
| [25] | CATALANO D, GEPPI M, MARINI A, et al. Orientational order properties in fluorinated liquid crystals from an optical, dielectric, and 13C NMR combined approach[J]. J Phys Chem C, 2007, 111(14): 5286-5299. DOI: 10.1021/jp066710u. |
| [26] | GEPPI M, MARINI A, VERACINI C A, et al. Orientational order of difluorinated liquid crystals: a comparative 13C-NMR, optical, and dielectric study in nematic and smectic B phases[J]. J Phys Chem B, 2008, 112(32): 9663-9676. DOI: 10.1021/jp800378g. |
| [27] | GEPPI M, MARINI A, MENNUCCI B, et al. Determination of order parameters in laterally fluorosubstituted terphenyls by 19F-NMR, optical and dielectric anisotropies[C]//Proceedings of the 23rd international liquid crystal conference (ILCC 2010) Part Ⅱ of Ⅷ. 2011, 541(1): 104-117. |
| [28] |
TANG Y Y, SUN P C, LIN H, et al. Dynamics of liquid crystalline phases in block copolymers studied by 2H-NMR spectroscopy[J].
Chinese J Magn Reson, 2005, 22(3): 253-259.
谭玉英, 孙平川, 林海, 等. 嵌段共聚物溶致液晶相中水的2H-NMR动力学分析[J]. 波谱学杂志, 2005, 22(3): 253-259. DOI: 10.3969/j.issn.1000-4556.2005.03.003. |
| [29] |
MA J H, GUO C, TANG Y L, et al. NMR studies on PEO-PPO-PEO block copolymers: A review[J].
Chinese J Magn Reson, 2008, 25(3): 421-434.
马俊鹤, 郭晨, 唐亚林, 等. PEO-PPO-PEO嵌段共聚物的NMR研究进展[J]. 波谱学杂志, 2008, 25(3): 421-434. DOI: 10.3969/j.issn.1000-4556.2008.03.018. |
| [30] |
ZHOU P, HU B W. Temperature-induced phase transitions in the silk gland of Bombyx mori silkworm lumen: A high-resolution solid-state 13C NMR study[J].
Chinese J Magn Reson, 2009, 26(1): 17-26.
周平, 胡炳文. 低温诱导桑蚕体内腺体相行为的高分辨13C固体核磁共振研究(英文)[J]. 波谱学杂志, 2009, 26(1): 17-26. DOI: 10.3969/j.issn.1000-4556.2009.01.002. |
| [31] | MULDER F A, FILATOV M. NMR chemical shift data and ab initio shielding calculations: emerging tools for protein structure determination[J]. Chem Soc Rev, 2010, 39(2): 578-590. DOI: 10.1039/B811366C. |
| [32] | HALLER I. Thermodynamic and static properties of liquid crystals[J]. Prog Solid State Chem, 1975, 10(2): 103-118. |
| [33] | CHIRTOC I, CHIRTOC M, GLORIEUX C, et al. Determination of the order parameter and its crytical exponent for nCB (n=5-8) liquid crystals from refractive index data[J]. Liq Cryst, 2004, 31(2): 229. DOI: 10.1080/02678290310001642540. |
| [34] | JADZYN J. On the molecular interpretation of the static dielectric properties of nematic liquid crystals[J]. Liq Cryst, 1999, 26(3): 437-442. DOI: 10.1080/026782999205218. |
| [35] | DUNMUR D A. The determination of molecular parameters from dielectric measurements on nematic liquid crystals[J]. Liq Cryst, 2005, 32(11/12): 1379-1387. |
| [36] | URBAN S, WÜRFLINGER A, GESTBLOM B. On the derivation of the nematic order parameter from the dielectric relaxation times[J]. Phys Chem Chem Phys, 1999, 1: 2787-2791. DOI: 10.1039/a901368g. |
| [37] | WU S T. Infrared markers for determining the order parameters of uniaxial liquid crystals[J]. Appl Opt, 1987, 26(16): 3434-3440. DOI: 10.1364/AO.26.003434. |
| [38] | PENCHEV I I, DOZOV I N. Anisotropic correction factors in the evaluation of nematic order parameters from polarized fluorescence measurements[J]. Mol Cryst Liq Cryst, 1981, 73(3/4): 267-271. |
| [39] | JONES W J, THOMAS D K, THOMAS D W, et al. On the determination of order parameters for homogeneous and twisted nematic liquid crystals from Raman spectroscopy[J]. J Mol Struct, 2004, 708(1/2/3): 145-163. |
| [40] | DE GENNES P G. Short range order effects in the isotropic phase of nematics and cholesterics[J]. Mol Cryst Liq Cryst, 1971, 12(3): 193-214. DOI: 10.1080/15421407108082773. |
| [41] | BUKA A, DE JEU W H. Diamagnetism and orientational order of nematic liquid crystals[J]. J Phys France, 1982, 43(2): 361-367. DOI: 10.1051/jphys:01982004302036100. |
| [42] | DRIES T, FUHRMANN K, FISCHER E W, et al. Magnetic susceptibility and order parameter of nematic liquid crystals as determined by a high-temperature SQUID magnetometer[J]. J Appl Phys, 1991, 69(11): 7539-7546. DOI: 10.1063/1.347571. |
| [43] | WEISS S M, OUYANG H M, ZHANG J D, et al. Electrical and thermal modulation of silicon photonic bandgap microcavities containing liquid crystals[J]. Opt Express, 2005, 13(4): 1090-1097. DOI: 10.1364/OPEX.13.001090. |
| [44] | KIM N, KYU T. Phase equilibria and photopolymerisation-induced phase transitions of mesogenic diacrylate monomer and low molecular mass liquid crystal mixture[J]. Liq Cryst, 2012, 39(6): 745-754. DOI: 10.1080/02678292.2012.678397. |
| [45] | SIEBERT H, BECKER P, QUIJADA-GARRIDO I, et al. In situ deuteron NMR investigations of sheared liquid crystalline polymers[J]. Solid State Nucl Magn Reason, 2002, 22(2/3): 311-326. |
| [46] | ZHOU W J, KORNFIELD J A, UGAZ V M, et al. Dynamics and shear orientation behavior of a main-chain thermotropic liquid crystalline polymer[J]. Macromolecules, 1999, 32(17): 5581-5593. DOI: 10.1021/ma990399f. |
| [47] | PELÁEZ J, WILSON M. Molecular orientational and dipolar correlation in the liquid crystal mixture E7: a molecular dynamics simulation study at a fully atomistic level[J]. Phys Chem Chem Phys, 2007, 9(23): 2968-2975. DOI: 10.1039/B614422E. |
 2019, Vol. 36
2019, Vol. 36 
