2. 湖南科技大学 化学化工学院, 理论有机化学与功能分子教育部重点实验室, 湖南 湘潭 411201
2. Key Laboratory of Theoretical Organic Chemistry and Functional Molecular Ministry of Education, School of Chemistry and Chemical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
化合物的各种物理化学性质之间存在内在联系,且这些联系在同一种分子结构衍生出来的系列化合物中是类似的[1].然而,目前对于化合物各种性质之间内在联系的表现形式,绝大多数尚不清楚.探明化合物性质之间的定量关系,则可以从易测定、费时少的性质去预测那些难测定而又费时多的物理化学性质[1],这也是化学工作者长期研究的重要内容之一.近30年以来,已有化学家对此领域进行过探索,并取得了令人欣喜的成绩[1-5].20世纪80年代,Needham等[2]对74个链烷烃的沸点、摩尔体积、摩尔折光率、蒸发热、表面张力、熔点、临界温度和临界压力这8种性质进行研究,结果发现沸点和临界温度,沸点和蒸发热,摩尔体积和摩尔折光率等性质之间存在很好的相关性.Screttas[3]研究得到单卤甲烷到四卤甲烷的生成焓与其卤原子和氢原子的电离能之和线性相关.Nau等[4]对二环和多环芳烃衍生物的氧化峰电位和垂直电离势之间的关系进行研究,并建立了相关参数方程.最近,曹晨忠等[1]根据化合物形成过程中价电子能量变化与生成焓之间的关系,推导出烷烃的生成焓和电离能之间的关系. Dong等[6]用Sverjensky-Molling线性自由能关系模型由已知的水溶液中阳离子的热力学参数来预测实验难以测定的二元锕系金属氧化物晶体的标准生成焓.以上研究结果表明化合物性质之间确实存在定量关系,同时,我们也注意到不同性质之间的相关方程形式多样,表达函数各不相同,有的简单,有的比较复杂.这意味着要研究诸多化合物性质两两相关,必须进行大量探索.到目前为止,化合物性能间的定量关系仅有极少部分被建立,还有待继续深入研究和发现.如今,实验条件不断改善,测试手段日益完备,化合物很多性质尤其是光谱性质的实验数据被大量获取.如何能将易测定的性质与难测定的性质之间建立起定量关系,既有重要的理论意义,又能解决许多实际问题,是一个令人感兴趣的重要课题.比如,核磁共振碳谱(13C NMR)相对而言易于测定,已经被广泛使用,而且目前的仪器精度可使测得的化学位移达到较高分辨率,因此获取大量化合物分子可靠的13C NMR数据并非难事.然而,作为化合物重要热力学参数之一的生成焓(
我们知道,烷烃分子CnH2n+2的键焓与生成焓之间存在以下关系:
| $ \sum {BD{E_{{\rm{C - X(X = C,H)}}}}} = n{\mathit{\Delta } _f}{H^0}({\rm{C}}) + (2n + 2){\mathit{\Delta } _f}{H^0}({\rm{H}}) - {\mathit{\Delta } _f}{H^0}({{\rm{C}}_n}{{\rm{H}}_{2n + 2}}) $ | (1a) |
(1a) 式中,
| $ \begin{array}{l} {\mathit{\Delta } _f}{H^0}({{\rm{C}}_n}{{\rm{H}}_{2n + 2}}) = n{\mathit{\Delta } _f}{H^0}({\rm{C}}) + (2n + 2){\mathit{\Delta } _f}{H^0}({\rm{H}}) - \sum {BD{E_{{\rm{C - X(X = C,H)}}}}} \\ {\rm{ }} = 2{\mathit{\Delta } _f}{H^0}({\rm{H}}) + n[{\mathit{\Delta } _f}{H^0}({\rm{C}}) + 2{\mathit{\Delta } _f}{H^0}({\rm{H}})] - \sum {BD{E_{{\rm{C - X(X = C,H)}}}}} \end{array} $ | (1b) |
(1b) 式中,
| $ {\mathit{\Delta } _f}{H^0}({{\rm{C}}_n}{{\rm{H}}_{2n + 2}}) = a + bn - \sum {BD{E_{{\rm{C - X(X = C,H)}}}}} $ | (2) |
(2) 式中,a和b为系数,且
通常,键焓的大小主要由两个成键原子的性质所决定,同时受到所处化学环境的影响.若用C-X键的标准键焓
| $ BD{E_{{\rm{C - X(X = C,H)}}}} = E_{{\rm{C - X(X = C,H)}}}^S + \mathit{\Delta } BD{E_{{\rm{C - X(X = C,H)}}}} $ | (3) |
对于烷烃,表征碳原子在分子中所处化学环境最直接、有效的参数就是其化学位移.如不考虑γ-邻位交叉效应(即较大基团对γ-位碳原子上的氢原子有空间挤压作用,使电子云偏向碳原子,从而使碳原子化学位移向高场移动),13C NMR化学位移则直接受到该原子电荷密度的影响.然而已有的研究[9-11]表明,烷烃分子中γ-邻位交叉效应使13C NMR化学位移向高场移动.因而为了得到碳原子上电荷密度与13C NMR化学位移的真实情况,必须对γ-邻位交叉效应所产生的影响进行校正.曹晨忠等[12]提出用三键数(P3)度量γ-邻位交叉效应对13C NMR化学位移的影响,得到很好的结果.因此,本文采用利用参数P3消除γ-邻位交叉效应影响后的13C NMR化学位移来表示
假定每个标准C-C键由两个处于“标准状态”(即不考虑所处化学环境影响)的碳原子连接而成,即C-C键的标准键焓为
| $ BD{E_{{{\rm{C}}_{\rm{1}}} - {{\rm{C}}_{\rm{2}}}}} = E_{{{\rm{C}}_{\rm{1}}} - {{\rm{C}}_{\rm{2}}}}^S + \mathit{\Delta } BD{E_{{{\rm{C}}_{\rm{1}}} - {{\rm{C}}_{\rm{2}}}}} \propto {\mathit{\delta } _{{{\rm{C}}_1}}} + {\mathit{\delta } _{{{\rm{C}}_2}}} = (\mathit{\delta } _{{{\rm{C}}_1}}^0 + \mathit{\Delta } {\mathit{\delta } _{{{\rm{C}}_1}}}) + (\mathit{\delta } _{{{\rm{C}}_2}}^0 + \mathit{\Delta } {\mathit{\delta } _{{{\rm{C}}_2}}}) $ | (4) |
假定标准C-H键中氢原子是与处于“标准状态”的碳原子连接而成,即C-H键的标准键焓为
| $ BD{E_{{\rm{C - H}}}} = E_{{\rm{C - H}}}^S + \mathit{\Delta } BD{E_{{\rm{C - H}}}} \propto {\mathit{\delta } _{\rm{C}}} = \mathit{\delta } _{\rm{C}}^0 + \mathit{\Delta } {\mathit{\delta } _{\rm{C}}} $ | (5) |
已知,烷烃分子CnH2n+2中有(n-1)个C-C键和(2n+2)个C-H键,因而(2)式中
| $ \sum {BD{E_{{\rm{C - X(X}} = {\rm{C,H)}}}}} = \sum\limits_{i = 1}^{n{\rm{ - 1}}} {BD{E_{{\rm{C - C,}}i{\rm{ }}}}} {\rm{ + }}\sum\limits_{i = 1}^{2n{\rm{ + 2}}} {BD{E_{{\rm{ C - H,}}i}}} $ | (6) |
由(4)式和(5)式可知,
| $ \sum {BD{E_{{\rm{C - X(X}} = {\rm{C,H)}}}} \propto 4\,} \sum\limits_{i = 1}^n {{\mathit{\delta } _{{{\rm{C}}_i}}}} = c + d\,\sum\limits_{i = 1}^n {{\mathit{\delta } _{{{\rm{C}}_i}}}} $ | (7) |
(7) 式中c、d是系数,
| $ \sum\limits_{i = 1}^n {{\mathit{\delta } _{{{\rm{C}}_i}}}} = g\sum\limits_{i = 1}^n {C{S_i}} + hP3 $ | (8) |
将(8)式代入(7)式得,
| $ \sum {BD{E_{{\rm{C - X(X}} = {\rm{C,H)}}}} = \,} c + d\sum\limits_{i = 1}^n {{\mathit{\delta } _{{{\rm{C}}_i}}}} = c + dg\sum\limits_{i = 1}^n {C{S_i}} + dhP3 $ | (9) |
为使用方便,我们将
| $ {\mathit{\Delta } _f}{H^0}({{\rm{C}}_n}{{\rm{H}}_{2n + 2}}) = e + fn + kSCS + jP3 $ | (10) |
(10) 式中,e, f, k和j为系数,可由数据拟合确定.
2 数据准备 2.1 13C NMR化学位移实测值之和(SCS)本文从有机化合物光谱数据库(Spectral Database for Organic Compounds,SDBS)摘录本文所用的大部分烷烃各碳原子的CS值(定标试剂:四甲基硅烷).碳原子数小于5的烷烃和其它个别烷烃各碳原子的CS值,由文献13, 14加以补充.由此共得到106个烷烃各碳原子的CS值(详见该文网页版附件表 1),用查得的CS值进行计算得到106个烷烃分子的SCS(表 1).
| 表 1 106个烷烃分子的n、SCS、P3及ΔfH0(kJ/mol)值 Table 1 The n, SCS, P3 and ΔfH0(kJ/mol) values of 106 alkanes |
P3指分子中距离给定碳原子有3个C-C键的片段总数,用于校正γ-邻位交叉效应对13C NMR化学位移影响.例如,C1-C2-C3-C4-C5-C6烷烃分子中有3个C-C-C-C片段,分别为C1-C2-C3-C4、C2-C3-C4-C5和C3-C4-C5-C6,则该分子的P3值为3.有一种情况需要特别注意,季碳原子上没有C-H键,它的γ-邻位交叉效应被忽略[12],与之相对应的片段不进行P3计数.例如,C1-C2(C6, C7)-C3-C4(C8)-C5分子中共有5个C-C-C-C片段,分别为C1-C2-C3-C4、C6-C2-C3-C4、C7-C2-C3-C4、C2-C3-C4-C5和C2-C3-C4-C8.但C2为季碳,所以端点为C2的片段不予考虑,也就是说上述5个片段中只计前3个,不计后2个,即该分子的P3值不是5,而只计为3.106个烷烃分子的P3值列于表 1.
3 结果与讨论 3.1 估算模型的建立为了考察(10)式的有效性,用从文献[15]中获得的53个烷烃分子生成焓实验值
| $ \begin{array}{l} {\mathit{\Delta } _f}H_{\exp }^0 = - 69.3783 - 7.3324n - 0.3592SCS - 2.3586P3\\ R = 0.9982,{\rm{ }}S = {\rm{3}}{\rm{.5 kJ/mol}},{\rm{ }}N = 53,{\rm{ }}F = 4452.52 \end{array} $ | (11) |
(11) 式中,R为相关系数,S为标准偏差,N为样本数,F为fisher值.结果表明,
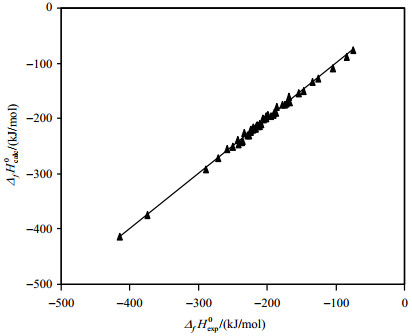
|
图 1 53个烷烃的生成焓实验值( |
为了检验本文模型的稳定性和预测能力,我们将样本分为训练集和测试集,先用留一法(leave-one-out method,LOO)对训练集进行交叉验证以检验模型的内部稳定性,再对测试集进行预测来考察模型对独立样本的预测能力.
首先,通过随机抽样法从53个样本(
| $ \begin{array}{l} {\mathit{\Delta } _f}H_{\exp }^0 = - 7.2832n - 0.3712SCS - 2.1253P3 - 68.6551\\ R = 0.9984,{\rm{ }}S = {\rm{3}}{\rm{.3 kJ/mol}},{\rm{ }}N = 42,{\rm{ }}F = 4009.22,{\rm{ }}{R_{CV}} = 0.9978,{\rm{ }}{S_{CV}} = 3.8{\rm{ kJ/mol}} \end{array} $ | (12) |
(12) 式的相关性很好,相关系数达0.998 4,标准偏差仅为3.3 kJ/mol.然后,用LOO法对(12)式进行验证,所得交叉验证相关系数和标准偏差(
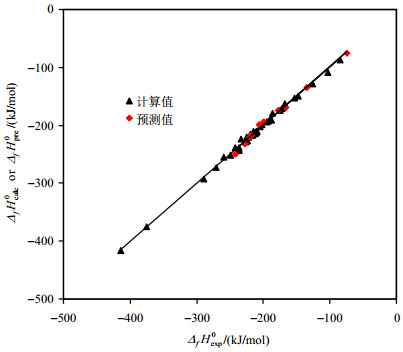
|
图 2 53个烷烃分子生成焓的计算值( |
最后,我们用(11)式对另外53个在文献[15]中未找到
最后,把从其他文献[16]或数据库(http://webbook.nist.gov/chemistry)获得的另外35个烷烃生成焓实验值(见表 1,第6列上标e或f)与利用(11)式计算的
| $ \begin{array}{l} {\mathit{\Delta } _f}H_{{\rm{calc}}}^0 = 1.0033{\mathit{\Delta } _f}H_{{\rm{exp}}}^0 + 1.8111\\ R = 0.9978,{\rm{ }}S = {\rm{3}}{\rm{.9 kJ/mol}},{\rm{ }}N = 35,{\rm{ }}F = 7480.42 \end{array} $ | (13) |
(13) 式的相关系数为0.997 8,计算值与实验值的平均绝对误差仅为2.9 kJ/mol,落于实验误差范围以内,可见利用(11)式预测烷烃的生成焓比较可靠.
4 结论综上所述,从烷烃13C NMR化学位移来预测生成焓是可行的,两者之间有明确的关联性.应该指出的是,迄今为止,对于烷烃生成焓的估算方法已提出多种,如经验方法、拓扑化学方法、神经网络方法以及量子化学方法等,但这些模型的建立都是基于分子结构信息或是电荷分布.而本文直接将烷烃13C NMR化学位移与生成焓关联起来,其意义不仅仅在于提出一个定量估算烷烃生成焓的新方法,更重要的是将看上去相差甚远的两种物理化学性能从理论上探索了它们之间的内在联系,这对于从同一分子结构基础上理解不同性能之间的联系提供了新的视角.当然,对于分子中含一个甚至多个杂原子的化合物(例如醇、醚和多卤代烷等),化学键类型变得更为复杂,影响其生成焓的因素也更多,这些化合物的生成焓与其化学位移之间的关系是否也具有本文提出的定量关系,有待进一步研究.
| [1] |
CAO C Z, LIU J L. Correlation between the ionization potential and enthalpy of formation for alkanes[J].
Acta Phys-Chim Sin, 2007, 23(6): 955-958.
曹晨忠, 刘金玲. 烷烃电离能和生成焓的相关性[J]. 物理化学学报, 2007, 23(6): 955-958. DOI: 10.3866/PKU.WHXB20070632. |
| [2] | NEEDHAM D E, WEI I C, SEYBOLD P G. Molecular modeling of the physical properties of alkanes[J]. J Am Chem Soc, 1988, 110(13): 4186-4194. DOI: 10.1021/ja00221a015. |
| [3] | SCRETTAS C, MICHA-SCRETTAS M. Correlation of thermochemical data with gas-phase ionization potentials[J]. J Org Chem, 1989, 54: 5132-5137. DOI: 10.1021/jo00282a033. |
| [4] | NAU W M, ADAM W, KLAPSTEIN D, et al. Correlation of oxidation and ionization potentials for azoalkanes[J]. J Org Chem, 1997, 62: 5128-5132. DOI: 10.1021/jo970574v. |
| [5] | KATRITZKY A R, GORDEEVA E V. Traditional topological indexes vs electronic, geometrical, and combined molecular descriptors in QSAR/QSPR research[J]. J Chem Inf Comput Sci, 1993, 33(6): 835-857. DOI: 10.1021/ci00016a005. |
| [6] | DONG W, YANG X J, ZHANG J, et al. Use of linear enthalpy relationship to predict standard enthalpies of formation of crystalline actinide dioxides[J]. Mater Lett, 2008, 62: 2894-2896. DOI: 10.1016/j.matlet.2008.01.066. |
| [7] | WINGET P, CLARK T. Enthalpies of formation from B3LYP calculations[J]. J Comput Chem, 2004, 25(5): 725-733. DOI: 10.1002/jcc.v25:5. |
| [8] | EMEL'YANENKO V N, KABO G J, VEREVKIN S P. Measurement and prediction of thermochemical properties:Improved increments for the estimation of enthalpies of sublimation and standard enthalpies of formation of alkyl derivatives of urea[J]. J Chem Eng Data, 2006, 51(1): 79-87. DOI: 10.1021/je050230z. |
| [9] | 宁永成. 有机化合物结构鉴定与有机波谱学[M]. 第二版. 北京: 科学出版社, 2000. |
| [10] | 朱淮武. 有机分子结构波谱解析[M]. 北京: 化学工业出版社, 2005. |
| [11] |
YI G Y, CAO C Z. Influence of substituent effects on the 13C NMR chemical shifts of aliphatic alcohols[J].
Chinese J Magn Reson, 2009, 26(1): 58-74.
易贵元, 曹晨忠. 取代基效应对脂肪醇13C NMR化学位移的影响[J]. 波谱学杂志, 2009, 26(1): 58-74. DOI: 10.3969/j.issn.1000-4556.2009.01.007. |
| [12] |
CAO C Z, LIU C, LIU S S, et al. Carbon atom distance edge vector and 13C NMR chemical shifts of alkanes[J].
Chinese J Magn Reson, 1998, 15(4): 347-353.
曹晨忠, 刘超, 刘树深, 等. 原子距边矢量、三键数与烷烃的13C NMR化学位移[J]. 波谱学杂志, 1998, 15(4): 347-353. |
| [13] |
LIU S S, YU B M, CAO C Z, et al. Study of 13C NMR spectroscopy:the chemical shift of alkane δ and the atom distance edge vector μ[J].
J Atom Mol Phys, 1997, 14(4): 606-614.
刘树深, 余般梅, 曹晨忠, 等. 核磁共振碳谱的研究:烷烃分子的化学位移δ与原子距边矢量μ[J]. 原子与分子物理学报, 1997, 14(4): 606-614. |
| [14] | LINDEMAN L P, ADAMA J Q. Carbon-13 nuclear magnetic resonance spectrometry.Chemical shifts for the paraffins through C9[J]. Anal Chem, 1971, 43(10): 1245-1252. DOI: 10.1021/ac60304a002. |
| [15] | HAYNES W M. CRC Handbook of chemistry and physics, 91st ed[M]. Boca Raton, FL: CRC Press, 2010-2011. |
| [16] | LABAUF A, GREENSHIELDS J B, ROSSINI F D. Heats of formation, combustion, and vaporization of the 35 nonanes and 75 decanes[J]. J Chem Eng Data, 1961, 6(2): 261-263. DOI: 10.1021/je60010a023. |
| [17] | CAO C Z, LIU S S, LI Z L. On molecular polarizability:2.Relationship to the boiling point of alkanes and alcohols[J]. J Chem Inf Comput Sci, 1999, 39(6): 1105-1111. DOI: 10.1021/ci990055o. |
| [18] |
CAO C Z, ZHOU F Y. Estimation formula for boiling point of hydrocarbon homologues and physical significance of coefficients[J].
Chem Bull, 1992, 11: 36-39.
曹晨忠, 周飞跃. 烃类同系物沸点通式及式中各系数的物理意义[J]. 化学通报, 1992, 11: 36-39. |
 2019, Vol. 36
2019, Vol. 36 
