文章快速检索     高级检索
  波谱学杂志   2019, Vol. 36 Issue (1): 45-54.  DOI: 10.11938/cjmr20182674
0

引用本文 [复制中英文]

刘焯, 欧阳传湘, 王长权, 等. 基于T2截止值的幂函数构建毛管压力曲线[J]. 波谱学杂志, 2019, 36(1): 45-54. DOI: 10.11938/cjmr20182674.
[复制中文]
LIU Zhuo, OU-YANG Chuan-xiang, WANG Chang-quan, et al. Construct NMR Capillary Pressure Curves by Piecewise Power Function Based on T2 Cutoff Values[J]. Chinese Journal of Magnetic Resonance, 2019, 36(1): 45-54. DOI: 10.11938/cjmr20182674.
[复制英文]

基金项目

国家自然科学基金资助项目（41302094）；吉林油田岩心分析化验评价项目（JLYT-XL-2017-JZTP-010）

通讯联系人

欧阳传湘, Tel:13908619951, E-mail:oycx@yangtzeu.edu.cn

文章历史

收稿日期：2018-08-04
在线发表日期：2018-09-29
Contents              Abstract              Full text              Figures/Tables              PDF
基于T2截止值的幂函数构建毛管压力曲线
刘焯 1, 欧阳传湘 1, 王长权 1, 韩登林 2, 吴琼 3, 高兴 3     
1. 长江大学 石油工程学院, 湖北 武汉 430100;
2. 长江大学 地球科学学院, 湖北 武汉 430100;
3. 吉林油田公司XL采油厂, 吉林 松原 138000
收稿日期：2018-08-04; 在线发表日期：2018-09-29
基金项目：国家自然科学基金资助项目（41302094）；吉林油田岩心分析化验评价项目（JLYT-XL-2017-JZTP-010）
通讯联系人(Corresponding author)：欧阳传湘, Tel:13908619951, E-mail:oycx@yangtzeu.edu.cn
摘要: 岩心核磁共振（NMR）T2谱和毛管压力曲线都在一定程度上反映了岩石孔隙结构，理论分析表明可利用T2谱构建毛管压力曲线，由此快速获取储层孔隙结构的信息.本文对18块岩样T2分布和毛管压力曲线进行了分析，提出将T2截止值作为幂函数的分段点，采用分段幂函数方法构建岩样的NMR毛管压力曲线，并与采用不分段幂函数方法获得的毛管压力曲线进行了对比.研究结果表明，与不分段幂函数方法相比，分段幂函数方法得到的结果和压汞实验测定的毛管压力曲线吻合度更高，平均拟合度（R2）达到0.943 1，并且论证了T2截止值作为分段点进行分段幂函数法构建NMR毛管压力曲线的合理性和可靠性.T2截止值的引入提高了幂函数法构建NMR毛管压力曲线的精度，是利用NMR T2谱构建岩样毛管压力曲线的有价值探索.
关键词: 低场核磁共振    毛管压力曲线    T2截止值    孔隙结构    
Construct NMR Capillary Pressure Curves by Piecewise Power Function Based on T2 Cutoff Values
LIU Zhuo 1, OU-YANG Chuan-xiang 1, WANG Chang-quan 1, HAN Deng-lin 2, WU Qiong 3, GAO Xing 3     
1. College of Petroleum Engineering, Yangtze University, Wuhan 430100, China;
2. College of Earth Sciences, Yangtze University, Wuhan 430100, China;
3. XL Oil Production Plant of Jilin Oilfield Company, Songyuan 138000, China
Abstract: To some extent, pore throat structures of the rock can be characterized by NMR T2 distribution and capillary pressure curve. Theoretical analysis showed that NMR T2 distribution of a rock could potentially be used to derive its capillary pressure curve, providing a quick and non-destructive way to obtain the pore structure distribution data of the reservoir. In this study, the capillary pressure curves of typical cores were constructed from nuclear magnetic resonance (NMR) T2 distributions using a piecewise power function method. T2 cutoff values were introduced as piecewise points for the power function. Then the capillary pressure curves constructed with the piecewise power function method and those constructed with the non-piecewise power function method were compared. The results showed that the proposed method had improved precision, with an averaged fitting degree of 0.943 1. Introducing of T2 cutoff values was proven to be useful in constructing NMR capillary curves by the piecewise power function method.
Key words: low-field NMR    capillary pressure curve    T2 cutoff value    pore structure    
引言

毛管压力曲线是研究岩石孔隙结构及多相渗流特性的重要依据，在实际油田生产中具有十分重要的意义.压汞法是获取岩心毛管压力曲线的重要手段，但该方法测试周期长，使用的汞毒性较强，且测试后岩心被污染不能重复使用，因此有一定的局限性.而核磁共振（NMR）横向弛豫时间（T2）分布与孔隙结构直接相关，理论上认为可利用T2谱构建NMR毛管压力曲线.与压汞法相比，NMR测量方法具有快速、无损等特点[1].因此，利用NMR T2谱获得岩心毛管压力曲线的方法在孔隙结构研究中具有广阔的应用前景.

目前，已有很多国内外学者提出了利用T2谱构建NMR毛管压力曲线的转化方法.转化方法主要分3类：（1）基于$ C = {p_c}/T_2^{ - 1} $（pc为毛管压力）公式[2, 3]的线性转化，或者是在此基础上引入可变刻度的改进方法[1]，改进方法中C是一个可变函数.但是线性转换得到的曲线在小孔径处吻合度并不好.可变刻度方法效果虽然有所改善，然而不同油藏可变刻度的经验公式也不同；（2）利用储层渗透率、孔隙度的综合指数建立NMR毛管压力曲线模型[4]，模型是由一组毛管压力关于储层渗透率或综合指数的经验公式组成，求取过程较为复杂；（3）采用单一幂函数转换[5]，或者分段进行线性或者幂函数拟合转换[6, 7]，但不同油田不同类型岩石的T2谱分段点不同，没有统一的分类标准.综上所述，目前利用T2谱构建NMR毛管压力曲线的方法比较常用的是线性和幂函数转换，其中，分段幂函数方法转换精度较高，但是关于其分段点的选择还缺乏详细的讨论与研究.

T2截止值（T2cf）定义为NMR T2谱上可动流体与束缚流体的分界值.大于T2cf的部分反映的是可动流体，存在于大孔隙中；小于T2cf的部分反映的是束缚流体，存在于小孔隙中[8]，因此T2cf是区分岩石大小孔径的关键参数.

基于上述前人的研究成果，本文对18块常规砂岩岩样分别进行NMR和压汞测试，通过对获得的T2谱和毛管压力曲线进行深入分析，提出将T2cf作为分段点，采用分段幂函数法构建NMR毛管压力曲线，结果表明该方法能够使构建的NMR毛管压力曲线更加可靠，不仅拓宽了幂函数法构建NMR毛管压力曲线的适用范围，也为NMR技术应用于岩石孔隙结构评价提供了更多的依据.

1 实验原理 1.1 T2谱与毛管压力曲线的理论关系

毛管压力与孔径之间的关系表示为：

$ {p_c} = \frac{{2\sigma \cos \theta }}{{{r_c}}} $ (1)

(1) 式中pc为毛管压力，单位为MPa；σ为流体界面张力，单位为N/m；θ为润湿接触角，单位为˚；rc为毛管半径，单位为μm.

由NMR弛豫机理可知[8]，T2表示为：

$ \frac{1}{{{T_2}}} = \frac{1}{{{T_{2{\rm{B}}}}}} + {\rho _2}\frac{S}{V} + \frac{{D(\gamma G{T_{\rm{E}}})}}{{12}} $ (2)

(2) 式中γ为旋磁比；T2B为流体的体积（自由）弛豫时间，单位为ms；D为自扩散系数，单位为μm2/ms；G为磁场梯度，单位为10-4 T/cm；TE为回波间隔，单位为ms；S为孔隙表面积，单位为cm2；V为孔隙体积，单位为cm3；ρ2为岩石的横向表面弛豫强度，单位为μm/ms.

通常对于饱和盐水的亲水岩石，T2B（2 000~3 000 ms）比T2大得多，当磁场均匀（G足够小）、TE足够短时，(2)式可简化[9]为：

$ \frac{1}{{{T_2}}} = {\rho _2}\frac{S}{V} $ (3)

由(3)式可知，驰豫时间T2与孔隙空间大小及形状结构有关.对于可以简化成球状孔隙、柱状管道的孔隙结构，其比表面（S/V）与孔径呈线性关系，而实际地层的孔隙界都很复杂，比表面与孔径呈非线性关系[6].目前大量研究表明，用非线性的幂函数对T2分布构建NMR毛管压力曲线的精度更高[6, 7, 10].则(3)式可表示为：

$ \frac{1}{{{T_2}}} = \frac{{{\rho _2}}}{{f({r_c})}} $ (4)

其中$ f({r_c}) $是一个关于孔径rc的幂函数，由(1)式和(4)式经过化简后可表示为[6, 10]：

${p_c} = m{(\frac{1}{{{T_2}}})^n} $ (5)

(5) 式中m、n为待求转换参数，拟合求出转换参数代入公式，即可将T2谱转换为NMR毛管压力曲线.

1.2 分段转换原因及分段点的选择

前人在研究NMR毛管压力曲线构建方法时，发现岩样在大孔、小孔处转换系数不同[1, 6, 7]，分析认为T2谱受到薄膜束缚水的影响，且束缚水对不同孔径T2谱信号的影响程度不同，因而转换系数不一样[7]（如图 1所示）.

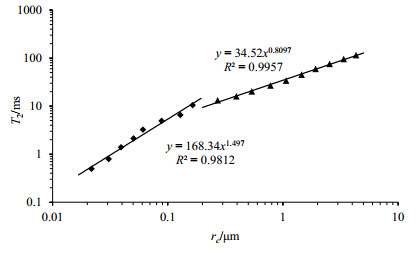
图 1 T2分布与毛管半径（rc）的关系 Fig. 1 Correlation between T2 and rc

在构建过程中，有学者依据T2图谱峰型分段转换：对于单峰用单一幂函数构建，对于有拐点的单峰则在拐点分段构建，双峰则选择在两峰之间的波谷处分段[7]；或者基于低渗透储层整体孔径小的特点，在大孔（> 1 μm）处采用线性公式$ C = {p_c}/T_2^{ - 1} $转换，在中孔（0.1~1 μm）和小孔（< 0.1 μm）处采用幂函数转换[8].但对于形态比较复杂的T2谱[11]分段点没有说明，而低渗透储层岩样与中高渗透岩样大小孔径的划分标准不同[12]，前者T2图谱转换的分段点不一定适用于的后者.

本文提出将T2cf作为分段点，因此构建NMR毛管压力曲线需要准确地标定T2cf.由于T2cf是识别、评价储层的关键参数，所以国内外学者对T2cf的确定做了大量研究.早期研究[13, 14]推荐经验值：砂岩T2cf取值33 ms，碳酸盐岩T2cf取值92 ms.但后期越来越丰富的研究数据表明不同地区、不同储层、不同岩性、不同物性的岩样T2cf存在很大差异[13-15]，不能再简单依靠经验标定T2cf.

目前，T2cf的确定方法包括离心实验法[13]、毛管压力曲线刻度法[10]、图谱形态法[11]、岩性判断法[16]、综合物性指数拟合回归方法[17]、基于正态分布函数的模拟预测法[18]、基于多重分形参数的多元线性回归预测法[19].其中，毛管压力曲线刻度法需要岩样的压汞测试资料；图谱形态法以及岩性判断法只能给出T2cf的范围；而回归预测方法则是基于大量实验数据得到的T2cf经验值，不适用于缺少相关资料的研究初期阶段.

本文采用的是比较常用的离心实验法确定T2cf.该方法在得到的离心前后岩样饱和水状态和束缚水状态下T2谱的基础上，利用孔隙度累加法[17]确定T2cf（原理如图 2所示）.合理选择离心力是保证该方法获得准确的T2cf的关键.我国行业标准《岩样核磁共振参数实验室测量规范》（SY/T6490-2014）推荐碳酸盐岩岩样和火山岩岩样的最佳离心力为2.758 MPa，不同渗透率级别（中高渗、低渗、超低渗）的碎屑岩的最佳离心力分别为0.689 MPa、1.379 MPa、2.068 MPa；周尚文等人[14]推荐页岩最佳离心力为2.76 MPa；李闽等人[20]推荐致密砂岩最佳离心力范围为2.758~3.103 MPa.

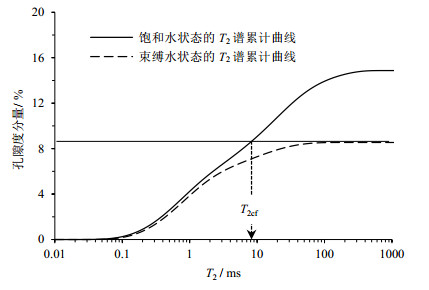
图 2 孔隙度累加法确定岩样T2cf原理图 Fig. 2 Principle diagram of rock sample T2cf determined by porosity summation
2 材料与方法 2.1 实验样品与实验条件

选取了吉林XL油田6口井具有代表性的18块亲水砂岩岩样进行NMR和压汞测试.温度25 ℃，湿度60~70%.实验用水为模拟地层水，矿化度为5 200 mg/L，密度为1.005 g/cm3.

2.2 实验仪器

NMR测试实验设备主要由NMR谱仪、岩心夹持器、恒速恒压泵、手摇泵和中间容器组成.NMR谱仪由上海纽迈科技生产，型号为MacroMR12-150H-I，磁场强度为(0.3±0.05) T，射频脉冲频率范围为1~30 MHz，频率控制精度为0.1 Hz，脉冲精度为100 ns.

压汞毛管压力曲线的测定设备是AutoPore Ⅳ 9510全自动压汞仪，最大进汞压力为241 MPa，对应的最小喉道半径约为0.003 μm.

2.3 实验步骤

（1）根据我国行业标准《岩心分析方法》（SY/T 5336-2006），测量岩样的长度、直径、干重、渗透率，将岩样抽真空饱和地层水，称量湿重.

（2）采集岩样饱和地层水状态下的T2谱，主要测试参数为：回波个数为2 500，回波时间间隔为0.2 ms，扫描32次，等待时间为5 000 ms，增益为50.

（3）根据我国行业标准《岩样核磁共振参数实验室测量规范》（SY/T 6490-2014）和调研[20]推荐的岩样最佳离心力值，结合碎屑岩储层渗透率级别分类（见表 1），可得到岩样对应的最佳离心力，采集离心后束缚水状态下岩样的T2谱，测量参数与步骤（2）相同.需要补充的是：文中测试的18块岩样渗透率级别包括中渗、低渗、特低渗、超低渗、致密，其中特低渗砂岩没有推荐的最佳离心力，因此在实验过程对特低渗岩样中依次采用0.689 MPa、1.379 MPa、2.068 MPa的离心力进行测试，当离心力逐渐增大时，若岩样内含水饱和度变化量在5%以内，则可认为此时的离心力为最佳压力[14].如图 3所示，当离心力从0.689 MPa增加到1.379 MPa时，岩样含水饱和度变化量为4.57%，当离心力从1.379 MPa增加到2.068 MPa时，岩样含水饱和度变化量为1.89%，几乎没有变化.因此，选择1.379 MPa作为本次特低渗透岩样离心实验的最佳离心力.

表 1 碎屑岩储层渗透率级别分类（《油气储层评价方法》SY/T 6285-2011 Table 1 Permeability graduation for clastic rock reservoir (Hydrocarbon reservoir evaluation method SY/T 6285-2011)
图 3 7号岩样的T2谱 Fig. 3 T2 spectra of No.7 rock sample

（4）将完成以上NMR测试的岩样重新洗油、烘干，根据我国行业标准《岩石毛管压力曲线的测定》（GB/T 29171-2012）进行压汞测试，获得毛管压力曲线（下文统一称为实测压汞曲线）.

2.4 数据处理

（1）按照图 2原理绘制岩样饱和水和束缚水状态的T2谱累计曲线，并得到岩样T2cf.

（2）将采集的岩样饱和水状态的T2谱反向累计获得NMR累计积分曲线，将累计分布频率作为NMR毛管压力曲线的横坐标，利用(5)式将T2分布转换为毛管压力pc，并作为NMR毛管压力曲线的纵坐标.

（3）将NMR毛管压力曲线和实测压汞曲线绘制在同一坐标系下，通过(5)式调整转换参数m、n，对实测压汞曲线进行拟合转换，获得拟合度更高的NMR毛管压力曲线.图 4展示了确定转换参数的具体过程.图 4(a)是保持参数n不变、改变参数m条件下获得的一系列曲线，由图 4(a)可以看出在参数n不变的前提下，改变参数m可以控制曲线的上下位置；图 4(b)是在参数m不变、改变参数n获得的一系列曲线，由图 4(b)可以看出在参数m不变的前提下，改变参数n可以调整曲线的斜率.如图 4(b)所示，在拟合转换过程中，实测压汞曲线在进汞饱和度（SHg）小的前半段与n=0.6的NMR毛管压力曲线吻合度高，而在进汞饱和度大的后半段与n=1.1的NMR毛管压力曲线吻合度更高，18块岩样在构建过程中均出现类似现象，因此有必要用两个不同的幂函数分段进行转换构建.

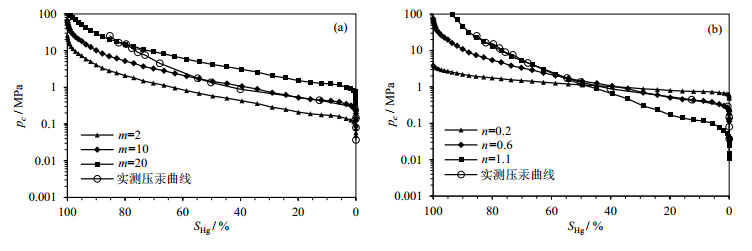
图 4 确定转换参数过程示意图 Fig. 4 Schematic for obtaining the conversion parameters m and n

（4）转换过程中先基于实际情况，根据(5)式调整一组参数m、n，构建不分段幂函数方法的NMR毛管压力曲线.

（5）根据(5)式调整2组参数m1、n1、m2、n2，使构建的2条曲线分别与实测压汞曲线的前半段和后半段最大程度吻合，分别取这两条曲线的半段组成分段幂函数方法构建的NMR毛管压力曲线，2条构建曲线的交点即为分段点，根据分段点对应的横坐标（SHg）按图 5的方法获得分段点对应的T2值，即分段点T2.将分段构建曲线和不分段法构造曲线与实测压汞曲线绘制在同一坐标系下进行比较.

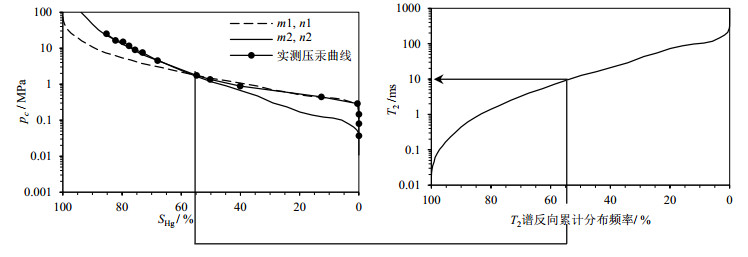
图 5 获得分段点T2值示意图 Fig. 5 Schematic diagram for obtaining the T2 value of piecewise point

（6）计算分段幂函数法构建曲线的拟合度.实测压汞曲线由序列$ {p_{ci}}\sim {S_{{\rm{Hg}}i}}(i = 1, 2, \cdots , n)$组成，选取NMR毛管压力曲线上横坐标与$ {S_{{\rm{Hg}}i}}(i = 1, 2, \cdots , n) $相同的点组成序列$ {\hat p_{ci}}\sim {S_{{\rm{Hg}}i}}(i = 1, 2, \cdots , n) $，由(7)~(9)式可计算得到：

${R^2} = 1 - SSE/SST $ (7)
$ SSE = \sum\limits_{i = 1}^n {{{({p_{ci}} - {{\hat p}_{c1}})}^2}} $ (8)
$ SST = \sum\limits_{i = 1}^n {{{({p_{ci}} - {{\bar p}_{c1}})}^2}} $ (9)

式中，R2为拟合度（回归决定系数）；SSE为残差平方和；SST为总离差平方和；$ {\bar p_{c1}} $为实测毛管压力平均值.

3 结果与讨论

实验测得了18块标准规格的天然砂岩岩样的物性参数资料、饱和水状态和束缚水状态下的T2谱，以及实测压汞曲线，在此基础上确定T2cf，并构建了NMR毛管压力曲线.

18块岩样的T2谱按图谱形态简单分为两类：单峰型、双峰型.岩样的T2cf、分段点T2值以及分段幂函数法构建曲线的拟合度见表 2.

表 2 18块砂岩岩样的物性参数、T2cf和分段拟合参数 Table 2 Physical properties, T2cf and piecewise fitting parameters of 18 sandstone samples

图 6(a1)~(a4)为其中4块岩样（岩样1、岩样5、岩样9、岩样18）的T2谱，图 6(b1)~(b4)为对应岩样采用分段和不分段幂函数方法构建的毛管压力曲线与压汞曲线对比图.如图 6所示，对于不同T2谱形态、不同渗透率级别的岩样，采用分段幂函数构建NMR毛管压力曲线与压汞毛管压力曲线的吻合度均高于不分段幂函数，18块岩样的拟合度均值达0.943 1，说明是用分段幂函数法的构建的结果是可信的.

图 6 不同岩样的饱和水和束缚水状态下的T2谱(a)，以及采用不同方法拟合的NMR毛管压力曲线与压汞毛管压力曲线的对比(b). (a1)和(b1)：岩样1；(a2)和(b2)：岩样5；(a3)和(b3)：岩样9；(a4)和(b4)：岩样18 Fig. 6 T2 spectra at saturated-water state and bound-water state (a), and the comparison of NMR capillary pressure curves fitting using two methods and mercury injection capillary pressure curve (b). (a1) and (b1): rock sample 1, (a2) and (b2): rock sample 5, (a3) and (b3): rock sample 9, (a4) and (b4): rock sample 18

将分段点T2值与离心法确定的岩样T2cf绘制散点图进行对比（图 7），可知二者数值基本吻合，误差很小.

图 7 分段点T2与T2cf对比图 Fig. 7 Comparison between T2 value of piecewise point and T2cf

上文提到NMR T2谱受到薄膜束缚水的影响；且孔径越小，受影响越大.本文分析认为，在大于T2cf的T2谱受到薄膜束缚水的影响很小，可以忽略不计；小于T2cf的T2谱受到薄膜束缚水的影响大，不能忽略.而压汞法是在真空中对洗净烘干的岩样用非润湿相汞驱替气，此时岩样中不存在薄膜束缚水.因此造成T2cf两边的T2谱与压汞毛管压力曲线的对应关系不同，并且分段的地方在T2cf附近.由此说明岩样T2cf可作为分段幂函数构建NMR毛管压力曲线的分段点.基于其区分可动流体与束缚流体的物理含义和拟合数据规律，将T2cf作为划分孔径的依据是合理的.

作者在研究过程中尚未遇到三峰型T2图谱的岩样，基于T2cf的分段幂函数构建NMR毛管压力曲线方法是否适用于该谱型还有待下步研究.

4 结论

（1）本文通过对18块砂岩岩样的NMR T2谱和压汞毛管压力曲线进行分析，提出了基于T2cf的分段幂函数构建NMR毛管压力曲线的方法，并与采用不分段幂函数方法获得NMR毛管压力曲线进行了对比，结果表明分段幂函数方法拟合效果更好，拟合度均值达0.943 1.

（2）分段幂函数法的分段点T2值与使用离心法获得的T2cf基本吻合，表明T2cf作为分段幂函数的分段点是合理可靠的.理论分析认为，T2cf两边的T2谱受到薄膜束缚水的影响程度不同，因此转换关系不同，需要在截止值处分段.

（3）基于T2cf的分段幂函数方法适用于图谱形态为单峰和双峰的常规砂岩岩样，该方法是否适用于复杂的三峰图谱还有待下步研究.


参考文献
[1] YAKOV V, WIM J L, WALTER F J S, et al. A practical approach to obtain 1st drainage capillary pressure curves from NMR core and log data[J]. Petrophisics, 2001, 42(4): 334-343.
[2] LI H B, ZHU J Y, GUO H S. Methods for calculating pore radius distribution in rock from NMR T2 spectra[J]. Chinese J Magn Reson, 2008, 25(2): 273-280.
李海波, 朱巨义, 郭和坤. 核磁共振T2谱换算孔隙半径分布方法研究[J]. 波谱学杂志, 2008, 25(2): 273-280. DOI: 10.3969/j.issn.1000-4556.2008.02.016.
[3] WANG S. Analysis of pore structure characteristics of rock by nuclear magnetic resonance[J]. Xinjiang Petroleum Geology, 2009, 30(6): 768-770.
王胜. 用核磁共振分析岩石孔隙结构特征[J]. 新疆石油地质, 2009, 30(6): 768-770.
[4] XIAO L, CHEN Z M, YUAN Y C. A novel method to construct capillary pressure curves by using NMR log data and its application in reservoir evaluation[C]. International Petroleum Technology Conference, 2008.
[5] LI A F, REN X X, WANG G J, et al. Characterization of pore structure of low permeability reservoirs using a nuclear magnetic resonance method[J]. Journal of China University of Petroleum, 2015, 39(6): 92-98.
李爱芬, 任晓霞, 王桂娟, 等. 核磁共振研究致密砂岩孔隙结构的方法及应用[J]. 中国石油大学学报(自然科学版), 2015, 39(6): 92-98. DOI: 10.3969/j.issn.1673-5005.2015.06.012.
[6] HE Y D, MAO Z Q, XIAO L Z, et al. A new method to obtain capillary pressure curve using NMR T2 distribution[J]. Journal of Jilin University (Geoscience), 2005, 35(2): 177-181.
何雨丹, 毛志强, 肖立志, 等. 利用核磁共振T2分布构造毛管压力曲线的新方法[J]. 吉林大学学报(地球科学版), 2005, 35(2): 177-181.
[7] YAN J P, WEN D N, LI Z Z, et al. The quantitative evaluation method of low permeable sandstone pore structure based on nuclear magnetic resonance(NMR)logging[J]. Chinese Journal of Geophysics, 2016, 59(4): 1543-1552.
闫建平, 温丹妮, 李尊芝, 等. 基于核磁共振测井的低渗透砂岩孔隙结构定量评价方法-以东营凹陷南斜坡沙四段为例[J]. 地球物理学报, 2016, 59(4): 1543-1552.
[8] GEORGE C, XIAO L Z, MANFRED P. Principle and application of NMR logging[M]. Beijing: Petroleum Industry Press, 2007.
[9] ZHOU S W, XUE H Q, GUO W, et al. Measuring movable oil saturation in reservoirs with low-field NMR technology[J]. Chinese J Magn Reson, 2015, 32(3): 489-498.
周尚文, 薛华庆, 郭伟, 等. 基于低场核磁共振技术的储层可动油饱和度测试新方法[J]. 波谱学杂志, 2015, 32(3): 489-498.
[10] 匡立春, 孙中春, 毛志强, 等. 核磁共振测井技术在准噶尔盆地油气勘探开发中的应用[M]. 北京: 石油工业出版社, 2015.
[11] ZHAO W Z, DING Y J, XIAO F, et al. On the method of determing the T2 cutoff value with the T2 spectrum characteristics[J]. Well Logging Technology, 2009, 33(5): 430-435.
邵维志, 丁娱娇, 肖斐, 等. 利用T2谱形态确定T2截止值的方法探索[J]. 测井技术, 2009, 33(5): 430-435. DOI: 10.3969/j.issn.1004-1338.2009.05.006.
[12] WANG Z Z, DENG M Y, ZHAI S D, et al. Factors affecting NMR T2 spectra of oil well samples and methods for determining the T2 cutoff value[J]. Chinese J Magn Reson, 2006, 23(1): 143-151.
王志战, 邓美寅, 翟慎德, 等. 油井样品NMR T2谱的影响因素及T2截止值的确定方法[J]. 波谱学杂志, 2006, 23(1): 143-151. DOI: 10.3969/j.issn.1000-4556.2006.01.016.
[13] ZHANG Y, LUO C. Study on the method for determining T2 cutoff value in NMR logging[J]. Standards and Quality of China Petroleum and Chemical, 2012, 33(14): 249.
张烨, 罗程. 核磁共振测井T2截止值的确定方法研究[J]. 中国石油和化工标准与质量, 2012, 33(14): 249. DOI: 10.3969/j.issn.1673-4076.2012.14.207.
[14] ZHOU S W, LIU H L, YAN G, et al. NMR research of movable fluid and T2 cutoff value of marine shale in South China[J]. Oil and Gas Geology, 2016, 37(4): 612-616.
周尚文, 刘洪林, 闫刚, 等. 中国南方海相页岩储层可动流体及T2截止值核磁共振研究[J]. 石油与天然气地质, 2016, 37(4): 612-616.
[15] WU F, SIMA L Q, YANG H M, et al. Research on NMR T2 cutoff of complex lithology in the West Qaidam Basin[J]. Well Logging Technology, 2014, 38(2): 144-149.
吴丰, 司马立强, 杨洪明, 等. 柴西地区复杂岩性核磁共振T2截止值研究[J]. 测井技术, 2014, 38(2): 144-149.
[16] QU X Y. Determination of T2 cutoff value of NMR logging in Bin Chang block[J]. Henan science and technology, 2015, 3: 129-130.
曲星远. 彬长区块核磁共振录井T2截止值确定方法[J]. 河南科技, 2015, 3: 129-130.
[17] YAN Z W, ZHANG H L, ZHOU X F, et al. A study on T2 cutoff value of ultralow permeability sandstone NMR in southwestern Ordos Basin, Minister 8[J]. Petroleum Geology and Engineering, 2015, 29(5): 128-131.
闫子旺, 张红玲, 周晓峰, 等. 鄂尔多斯盆地西南部长8超低渗透砂岩核磁共振T2截止值研究[J]. 石油地质与工程, 2015, 29(5): 128-131. DOI: 10.3969/j.issn.1673-8217.2015.05.037.
[18] GE X M, FAN Y R, ZHU X J, et al. Determination of nuclear magnetic resonance T2 cutoff value based on multifractal theory -An application in sandstone with complex pore structure[J]. Geophysics, 2015, 80(1): D11-D21. DOI: 10.1190/geo2014-0140.1.
[19] XIAO L, LI J R, MAO Z Q, et al. A method to determine nuclear magnetic resonance (NMR) T2 cutoff based on normal distribution simulation in tight sandstone reservoirs[J]. Fuel, 2018, 225: 472-482. DOI: 10.1016/j.fuel.2018.03.178.
[20] LI M, WANG H, CHEN M. Distribution characteristics and influencing factors of movable fluid in tight sandstone reservoirs:a case study of Lucaogou Formation in Jimsar Sag, NW China[J]. Lithologic Reservoirs, 2018, 30(1): 140-149.
李闽, 王浩, 陈猛. 致密砂岩储层可动流体分布及影响因素研究——以吉木萨尔凹陷芦草沟组为例[J]. 岩性油气藏, 2018, 30(1): 140-149. DOI: 10.3969/j.issn.1673-8926.2018.01.014.