半晶高分子的相结构和其性能之间的关系一直是高分子科学研究的一个重要课题.半晶高分子的相结构类型和相对含量对高分子材料密度、热性能和机械性能等材料性质有巨大影响.通常来说,半晶高分子的相结构类型包括结晶相、非晶相,以及结晶相与非晶相之间的界面相[1-4].研究半晶高分子相结构的方法主要有热分析法、密度法、红外光谱法和X射线衍射测量法等.这些方法从各自的角度给出了半晶高分子的相结构类型、含量方面的信息.但这些方法常常由于测量原理的限制,无法同时观测半晶高分子的结晶相、非晶相,以及结晶相与非晶相之间的界面相.值得一提的是由于半晶高分子结晶相与非晶相之间结构渐变的特性,结晶相与非晶相之间的界面相通常同时具有晶相和非晶相的结构特征.这一结构特性使得对半晶高分子结晶相与非晶相之间界面相的观测成为半晶高分子相结构观测和研究的难点[5-7].
宽线固体核磁共振氢谱(1H NMR)是一种研究半晶高分子相结构的经典方法.该方法通过对NMR频域谱进行分峰拟合,获得信号中宽窄峰的比例,从而得到高分子相结构的含量和分布信息. Chen等[8]利用Gaussian/Lorentzian多组分函数对聚(3-羟基丁酸酯)均聚物结构拟合,并对材料的相结构进行归属,获得材料中各个相结构的相对含量.然而在利用宽线固体1H NMR谱研究高分子相结构的实际工作中,仅利用Gaussian或Lorentzian函数的叠加拟合常常遇到拟合不完善的问题.特别是在刚性很强的相结构中,结晶区信号的线型并不是理想的Gaussian线型,而是需要用更复杂的函数形式来描述[9-12].为此一些研究者尝试对自由感应衰减信号(FID)进行拟合[7, 13-17],而直接拟合该类高分子的宽线固体1H NMR谱的研究工作鲜有报道.常用的拟合软件Dmfit中也不具备该功能选项.本文利用傅里叶变换后的Gaussian/Sinc、Gaussian和Lorentzian函数对半晶聚乙烯的宽线固体1H NMR谱进行了拟合,实现了良好的信号拟合效果.基于对宽线固体1H NMR谱的归属,我们进一步研究了半晶聚乙烯各相结构中分子链的运动性与线型的相关性,探讨了利用宽线固体1H NMR实验测量半晶高分子结晶度的可行性.
1 实验部分 1.1 仪器与试剂样品:超高分子量聚乙烯(PE)由荷兰Maastricht大学Sanjay Rastogi教授提供,平均分子量为630万.
扫描电子显微镜(SEM)实验在Carl Zeiss LEO 1530 VP场发射电镜上进行,加速电压为5.0 kV.
宽线固体1H NMR实验在Bruker AVANCE Ⅲ 300型固体NMR谱仪上进行,1H核共振频率为300.16 MHz,高功率射频脉冲时间为2.5 μs,采样间隔为0.4 μs,采样时间为2 ms,每个实验的循环等待时间(Recycle delay)为60 s. 1H NMR谱的化学位移是以金刚烷(Adamantane)信号(δH 1.46)为参考定标.变温实验中,每个温度稳定5 min后再进行采样,数据处理用Topspin软件进行,数据拟合在Dmfit和Matlab软件上进行.
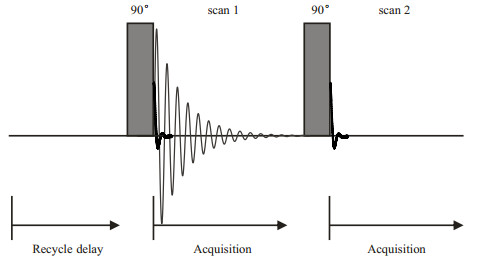
1.2 实验所用脉冲序列为了消除FID信号中探头的背景信号,我们采用了1H EASY脉冲序列采集宽线固体1H NMR谱. 1H EASY脉冲序列如图 1所示.首先,对1H核用90˚脉冲激发后采样,此时激发的信号中既包括样品的信号,也包含背景信号.由于探头的背景信号大都来源于线圈周围的环境,其信号不遵循通常的T1弛豫行为. EASY序列利用背景信号的这一个弛豫特性,通过两次激发和信号采集消除背景信号.原理大致如下:第一个90˚脉冲后采集的信号包括样品的信号和背景信号.在第一个脉冲激发信号完全横向弛豫后,再激发一个相同的90˚脉冲并进行采样.此时采集到的主要是背景信号.两次信号相减就可以得到去除背景后的样品信号.具体EASY脉冲序列的原理请参见文献[18].
|
图 1 1H EASY脉冲序列 Fig. 1 1H EASY pulse sequence |
宽线固体1H NMR研究中,通常以Lorentzian函数拟合运动性较强的非晶相1H FID信号[9],Lorentzian函数的形式为:
| $ {I_{\rm{1}}}(t) = {I_{\rm{0}}}\exp ( - \frac{t}{{{T_{{\rm{2a}}}}}}) $ | (1) |
(1) 式Fourier变换后的形式为
| $ {F_{\rm{1}}}(v) = \frac{{\sqrt 2 {I_0}{T_{{\rm{2a}}}}}}{{\sqrt {\rm{ \mathit{ π} }} }}\frac{1}{{{{(2{\rm{ \mathit{ π} }}v{T_{{\rm{2a}}}})}^2} + 1}} $ | (2) |
其中:I1(t)为实验时间t时1H FID信号强度,I0为1H FID初始的信号强度,t为信号衰减的时间,T2a为非晶相横向弛豫时间,v为频率.
Gaussian函数通常被用来拟合高分子刚性结构(包括高分子结晶相和刚性非晶结构)中的1H FID信号[9].其函数形式为:
| $ {I_{\rm{2}}}(t) = {I_0}\exp \left[ { - {{(\frac{t}{{{T_{2{\rm{c}}1}}}})}^2}} \right] $ | (3) |
(3) 式Fourier变换后的形式为
| $ {F_{\rm{2}}}(v) = \frac{{{I_0}}}{{\sqrt {{\rm{2 \mathit{ π} }}} }}\int_0^T {\exp \left\{ { - \left[ {{{(\frac{t}{{{T_{{\rm{2c1}}}}}})}^2} + {\rm{i}}2{\rm{ \mathit{ π} }}vt} \right]} \right\}{\kern 1pt} } \, {\rm{d}}t $ | (4) |
其中:I2(t)为实验时间t时1H FID信号强度,I0为1H FID初始的信号强度,t为信号衰减的时间,T2c1为刚性结构的横向弛豫时间,v为频率.
高分子材料中高度刚性部分,例如高结晶度高分子材料的结晶相,可以通过Gaussian/Sinc函数拟合其1H FID信号[7, 13-17],其函数形式为:
| $ {I_{\rm{3}}}(t) = {I_0}\left\{ {\exp \left[ { - {{(\frac{t}{{{T_{{\rm{2c2}}}}}})}^2}} \right]} \right\}{\kern 1pt} \, \frac{{\sin bt}}{{bt}} $ | (5) |
(5) 式Fourier变换后的形式为
| $ {F_{\rm{3}}}(v) = \frac{{\sqrt {\rm{2}} {\rm{ \mathit{ π} }}{T_{{\rm{2c2}}}}{I_0}}}{b}\int_{(v - b)/2{\rm{ \mathit{ π} }}}^{(v + b)/2{\rm{ \mathit{ π} }}} {\exp \left[ { - {{({\rm{ \mathit{ π} }}{T_{{\rm{2c2}}}}\sigma )}^2}} \right]} {\kern 1pt} \, {\rm{d}}\sigma $ | (6) |
其中:I3(t)为实验中时间t时1H FID信号强度,I0为1H FID初始的信号强度,σ为I3(t)傅里叶变换的分部积分所用的时间微分,T2c2为高度刚性成分的横向弛豫时间,b是震荡因子,v为频率.
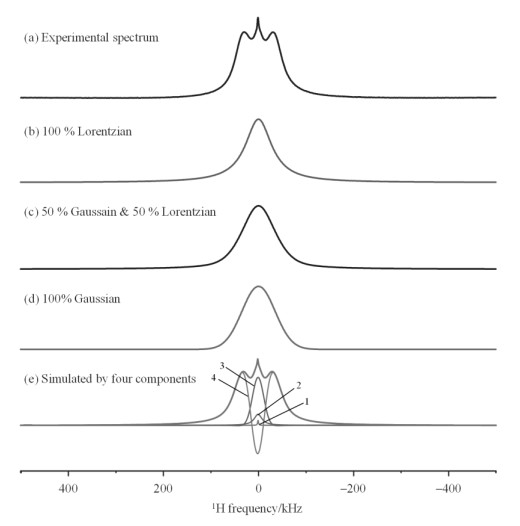
2 结果与讨论 2.1 PE样品的宽线固体1H NMR谱拟合函数选择图 2(a)是30 0 K下PE样品的宽线固体1H NMR谱.从图中可以发现,该信号由一个两边凸起中间下凹的宽峰信号以及两个半高宽不同的尖峰信号组成.谱图的半高宽(FWHM)为105 kHz.其中,信号主要成分——两边凸起中间下凹的宽峰信号无法利用Lorentzian函数[图 2(b)]、Lorentzian/Gaussian函数[图 2(c)]以及Gaussian函数[图 2(d)]进行拟合.按文献[7, 13-17]报道,两边凸起中间下凹的宽峰信号可以通过Gaussian/Sinc函数进行拟合. 图 2(e)是采用含有两个Lorentzian函数、1个Gaussian函数和1个Gaussian/Sinc函数的组合进行拟合获得的谱图.比较图 2(a)和图 2(e)可以发现,图 2(e)的拟合信号和原始谱图匹配度很高.接下来我们将对图 2(e)的拟合过程,特别是图 2(e)中拟合得到的4种信号成分的来源,做详细讨论.
|
图 2 (a) PE样品的宽线固体1H NMR谱,实验温度为300 K;(b) Lorentzian函数拟合谱(δH 0,FWHM=84 kHz);(c) Lorentzian/Gaussian函数拟合谱(δH 0,FWHM = 103 kHz,Lorentzian/Gaussian=1);(d) Gaussian函数拟合谱(δH 0,FWHM = 100 kHz);(e)通过包含4个函数的组合拟合的谱图[Lorentzian 1函数(线型1),Lorentzian 2函数(线型2),Gaussian函数(线型3)和Gaussian/Sinc函数(线型4),拟合参数见下文] Fig. 2 (a) Experimental wide-line solid-state 1H NMR spectrum of polyethylene at 300 K. The spectra were fitted by using (b) a Lorentzian function (δH 0, FWHM = 84 kHz), (c) a Lorentzian/Gaussian function (δH 0, FWHM = 103 kHz, Lorentzian/Gaussian=1), (d) a Gaussian function (δH 0, FWHM = 100 kHz) and (e) a combination of four functions [Lorentzian 1 (lineshape 1), Lorentzian 2 (lineshape 2), Gaussian (lineshape 3), Gaussian/Sinc (lineshape 4). The fitting parameters are discussed later] |
图 3(a)为所用半晶PE样品的SEM图.从图中可以明显看出,样品主要由片晶结构组成,片晶的厚度约为20 nm.通常认为高分子片晶是由高分子链通过折叠形成. 图 3(b)是PE片晶结构的模型图.在该模型图中黑线表示高分子链.高分子链通过折叠的形式形成片晶,分子链折叠结构组成了样品非晶结构的主体部分.结晶分子链段受到晶格的限制,运动能力非常弱,1H-1H偶极相互作用强,1H NMR谱峰的宽度通常非常宽.对于非晶链来说,分子链的运动与非晶区的玻璃化转变温度(Tg)有关[19-21].在Tg温度以上,PE非晶分子链段受到分子链排列的限制小,运动能力较强.较强的分子运动能够大幅削弱1H-1H偶极相互作用.因此,在Tg温度以上PE非晶分子链1H NMR谱峰的宽度通常较窄.文献中报道的PE的Tg范围很大,不过多数研究认为PE的Tg低于室温.通常来说,半晶高分子结晶/非晶之间还存在界面相[22].界面相中分子链排列具有一定的有序程度,满足从非晶无序结构到结晶有序结构的过渡要求.如果仔细考虑到结晶/非晶界面的构造,界面结构还可以细分为界面相中靠近结晶相的部分和靠近非晶相的部分[23].界面相中靠近结晶相部分的分子链可能受结晶结构的影响而具有接近结晶相本体的排列结构,相应的分子链运动会受到更多限制.而界面相中靠近非晶相部分的分子链可能受结晶结构的影响较小其分子链排列结构更可能接近于非晶结构,相应的分子链运动会受到较小的限制.分子链段运动能力不同,对1H-1H偶极相互作用的调制/削弱程度也不同,由此导致1H NMR信号不同的线型和线宽.在以下工作中我们将基于上述PE的相结构模型,对PE的宽线固体1H NMR谱进行拟合和研究.

|
图 3 (a) PE的SEM图;(b) PE相结构模型 Fig. 3 (a) SEM image of the polyethylene; (b) Phase structure model of polyethylene |
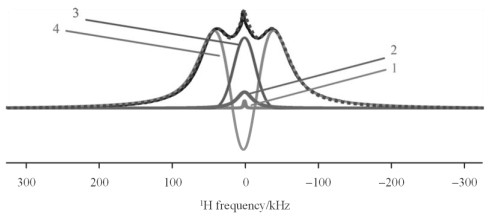
图 4是300 K时PE样品的宽线固体1H NMR实验谱图和拟合谱图.为了获得实验谱图与拟合谱图的高匹配程度,该实验谱图需要对4个信号成分进行拟合:信号成分1采用Lorentzian函数拟合,其半高宽很窄,表明这部分信号对应的分子链段运动性最强,我们将其归属为材料中的非晶相.信号成分2采用Lorentzian函数拟合,其半高宽较宽,我们将其归属为材料中受限的非晶成分,其来源之一可能是结晶/非晶界面相中的非晶成分.信号3采用Gaussian函数拟合,其半高宽较宽.根据该信号的弛豫形式和T2值,我们将其归属为材料中较为刚性的成分,其来源之一可能是结晶/非晶界面相中的结晶部分或结晶相中的结晶缺陷.信号4采用Gaussian/Sinc函数拟合.该函数可以给出呈两边凸起的谱峰形状,该信号在频谱上分布较宽,我们将其归属为材料中最为刚性的成分——结晶相本体.虚线是4个信号成分叠加后的结果.可以看到,这个信号与实验谱图(图 4中除1、2、3、4外的另外一条实线)的匹配度非常高. 表 1给出了通过信号拟合获得的各个信号的含量.
|
图 4 PE样品的宽线固体1H NMR实验谱图(除1、2、3、4外的另外一条实线)和拟合谱图(虚线).拟合谱图由采用不同函数拟合的4个信号成分组成:Lorentzian 1函数(线型1);Lorentzian 2函数(线型2);Gaussian函数(线型3);Gaussian/Sinc函数(线型4).实验在300 M NMR谱仪上进行,温度为300 K Fig. 4 The experimental (solid line except 1, 2, 3, 4) and simulated (dash line) wide-line solid-state 1H NMR spectra of polyethylene. The simulated spectrum consists of 4 signal components fitted with 4 functions including: Lorentzian 1 (lineshape 1), Lorentzian 2 (lineshape 2), Gaussian (lineshape 3), Gaussian/Sinc (lineshape 4). The experiment spectrum was acquired on a 300 M NMR instrument at 300 K |
| 表 1 300 K时PE样品的宽线固体1H NMR谱拟合获得的T2值和信号成分分析 Table 1 T2 fitting and signal component analysis for wide-line solid-state 1H NMR spectrum of polyethylene acquired at 300 K |
图 5是PE样品在不同温度下的宽线固体1H NMR谱及其拟合谱图. 280 K时,PE样品的宽线固体1H NMR谱中由Gaussian/Sinc函数拟合的信号(线型4)很明显,两个Lorentzian函数拟合的尖峰信号(线型1和2)很弱.通过比较图 5中不同温度下的信号,我们发现随着温度的升高,宽峰(线型3)的信号逐渐降低,线型4的信号明显减弱,同时线型1和2的信号逐渐增强.这表明随温度升高,PE样品相结构的性质发生了显著变化. 表 2中给出了不同温度下PE样品的宽线固体1H NMR谱拟合的参数.

|
图 5 不同温度下PE样品的宽线固体1H NMR实验谱图(除1、2、3、4外的另外一条实线)和拟合谱图(虚线).拟合谱图由采用不同函数拟合的4个信号成分组成:Lorentzian 1函数(线型1);Lorentzian 2函数(线型2);Gaussian函数(线型3);Gaussian/Sinc函数(线型4) Fig. 5 The experimental (solid line except 1, 2, 3, 4) and simulated (dash line) wide-line solid-state 1H NMR spectra of polyethylene at different temperatures. Each simulated spectrum consists of 4 signal components fitted with 4 functions: Lorentzian 1 (lineshape 1), Lorentzian 2 (lineshape 2), Gaussian (lineshape 3), Gaussian/Sinc (lineshape 4) |
| 表 2 不同温度下PE样品的宽线固体1H NMR谱的拟合 Table 2 T2 fitting for wide-line solid-state 1H NMR spectra of polyethylene at different temperatures |
图 6为Gaussian/Sinc函数拟合的成分的T2c2值和b值随温度的变化曲线.从图中可以发现T2c2值随温度升高出现一定的升高趋势,b值随着温度的升高而降低,其原因可以部分归结于在升温过程中PE晶格膨胀导致1H-1H偶极相互作用降低.这些现象与文献[24]报道一致.

|
图 6 Gaussian/Sinc函数拟合的信号成分的(a)T2c2和(b)b值随温度的变化曲线 Fig. 6 T2c2 (a) and b (b) values of the signal component fitted using Gaussian/Sinc function changed with temperature |
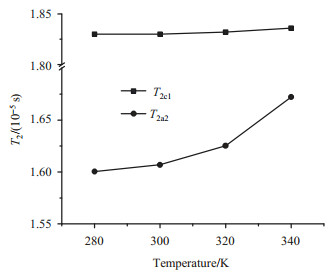
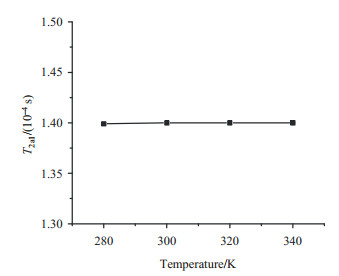
图 7给出了Gaussian函数拟合的信号成分的T2c1和Lorentzian 2函数拟合得到的信号成分的T2a2值随温度变化的曲线.随温度的升高,T2c1基本保持不变.这是因为结晶界面上的分子尽管排列比较松散,但仍受到晶格的束缚,温度升高对晶格膨胀影响较小,1H-1H偶极相互作用变化不大.与之相比,Lorentzian函数拟合的非晶界面部分,其T2a2随着温度上升,升高比较明显.这可能是由于该成分为非晶成分,并不受到晶格束缚,由此分子链的运动性随温度升高而大幅增强. 图 8是Lorentzian函数拟合的非晶部分的T2a1随温度的变化曲线.从数值看,非晶部分的衰减常数T2a1在相同温度下和界面相、非晶相相比要大近一个数量级,表明其衰减的时间最长.说明该部分链段偶极相互作用最弱、运动性最强.随着温度升高,T2a1基本不变.这可能是非晶部分在高分子体系中本身运动性已经非常高,因而在本实验温度区间内,随着温度升高,其运动性变化不如其他成分变化明显.
|
图 7 Gaussian函数拟合获得的信号成分的T2c1和Lorentzian 2函数拟合获得的信号成分的T2a2随温度的变化曲线 Fig. 7 T2c1 of the signal component fitted using Gaussian function, and T2a2 of the signal component fitted using Lorentzian 2 function changed with temperature |
|
图 8 Lorentzian 1函数拟合获得的信号成分的T2a1随温度的变化曲线 Fig. 8 T2a1 of the signal component fitted using Lorentzian 1 function changed with temperature |
在上述1H NMR谱图拟合分析过程中, 我们把Gaussian/Sinc函数拟合的信号成分归属为结晶相, Gaussian函数拟合的信号成分归属为界面相中结晶成分, 两个Lorentzian函数拟合的信号成分分别归属为界面相中非晶成分和非晶相.基于上述归属, 下面我们将从这些信号成分的含量探讨材料"结晶度"的观测.为了评价通过宽线固体1H NMR谱获得的结晶度的准确性, 我们利用定量13C魔角旋转(MAS)实验对同一材料的结晶度进行了观测. 图 9是该样品的定量13C MAS NMR谱图和拟合结果.考虑到样品中13C核自旋的长弛豫特征, 采集定量13C MAS谱图时, 我们将实验的循环等待时间设为3 000 s.由于300 K温度下该PE样品的13C核的T1约为400 s, 所以3 000 s的循环等待时间可以确保该样品13C NMR信号完全弛豫.根据文献[25, 26]报道, δC 33.0的NMR信号峰属于all-trans构象的正交晶体的信号, δC 34.2的NMR信号峰属于all-trans构象的单斜晶中的信号, 二者都属于材料中的结晶信号. δC 31.0处的NMR信号归属于材料中的非晶信号.根据以上信号归属, 定量13C MAS NMR谱图显示该样品的结晶度约为76%.

|
图 9 PE样品的定量13C MAS NMR谱图和拟合结果.谱图通过单脉冲激发采集,循环等待时间3 000 s.实验温度为300 K Fig. 9 The quantitative 13C MAS NMR spectrum of polyethylene and the fitting results. The spectrum was acquired via single pulse excitation with a recycle delay of 3 000 s at 300 K |
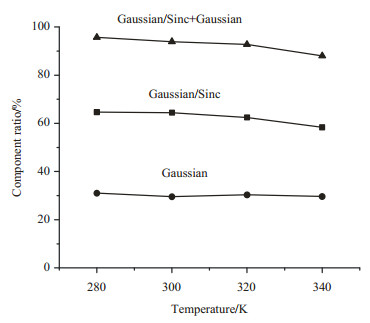
图 10是280 K到340 K,Gaussian函数和Gaussian/Sinc函数拟合得到的成分含量随温度的变化情况.为方便比较,我们将二者加和含量也随温度变化做图(Gaussian/Sinc + Gaussian).随着温度升高,Gaussian函数拟合得到的成分的含量基本不变,Gaussian/Sinc函数拟合得到的成分含量逐渐降低,二者加和的含量也呈逐渐降低的趋势.如果Gaussian/Sinc和Gaussian拟合的成分含量总和归属为材料的“结晶度”,那么这个PE样品的“结晶度”将会很高,在280 K时超过了90%,即使到340 K时也超过了85%.这过高的“结晶度”远超13C MAS NMR所测得的结晶度.如果将Gaussian/Sinc函数拟合得到的成分含量认为是材料的“结晶度”,那么该材料的“结晶度”只有65%左右,这一数值又明显低于13C MAS NMR所测得的结晶度.我们认为造成这一现象的主要原因在于对Gaussian函数拟合得到的信号成分的归属.在上述讨论中,我们根据该信号成分所具有弛豫性质将其归属为结晶界面中靠近结晶相的结构.由于分子链段运动能力与分子链的构象并不存在直接的联系,能形成Gaussian线型信号的高分子链并一定要采取all-trans构象.所以,即使我们假定最刚性成分,Gaussian/Sinc函数拟合得到的信号成分,完全来源于结晶相的all-trans构象分子链,然而不管是单独Gaussian/Sinc函数拟合得到的成分含量,还是Gaussian/Sinc和Gaussian函数拟合得到的成分含量总和都不能代表样品中结晶相all-trans构象分子链的总和.而在定量13C MAS NMR中,信号成分是否能被归属为结晶信号,完全取决于该成分中分子链是采取了all-trans构象(δC 33.0或者δC 34.2)或者gauche构象(δC 31.0).因此,从定量13C MAS NMR中获得的结晶度与宽线固体1H NMR谱中Gaussian函数和Gaussian/Sinc函数拟合得到的成分含量并不具备可比性.
|
图 10 不同温度下PE样品的宽线固体1H NMR谱中Gaussian函数、Gaussian/Sinc函数拟合的成分,以及两者总和的含量变化.温度范围为280~340 K Fig. 10 The component ratio of wide-line solid-state 1H NMR spectrum contents fitted using Gaussian function, Gaussian/Sinc function, and their summation at different temperatures. The temperature range was 280~340 K |
假定最刚性信号(Gaussian/Sinc函数拟合的成分)中分子链都是采取all-trans构象,Lorentzian函数拟合的成分都采取gauche构象,那么Gaussian函数拟合的成分所对应的相结构中分子链应该同时存在all-trans和gauche构象.如果这一推论成立,那么我们可以进一步思考Gaussian函数拟合的成分所对应的相结构中采取all-trans和gauche构象的分子链为什么会给出类似的宽线固体1H NMR线型.由于宽线固体1H NMR信号的线型与分子链的运动性密切相关,类似的宽线固体1H NMR线型暗示采取all-trans和gauche构象的分子链具有类似的运动性.我们认为这种具有类似运动性的all-trans和gauche构象很可能是界面结构中分子链构象的典型特征.这也从一定程度上验证了我们对Gaussian函数拟合的成分的归属.考虑到样品非晶区的链折叠结构很可能导致较高的受限非晶结构含量以及较大的非晶/结晶界面相含量(即非晶到结晶的过渡区).这些相结构因素最终造成了宽线固体1H NMR中较高的Gaussian函数拟合的成分含量.
3 结论本文基于Gaussian/Sinc、Gaussian和Lorentzian函数成功拟合了PE样品的宽线固体1H NMR谱,并根据结晶相非晶/结晶界面相,以及非晶相,对各个信号成分进行了归属.通过变温实验研究了宽线固体1H NMR谱中各信号成分的温度依赖性,并由此探讨了不同相结构中分子链运动温度依赖性:随温度升高,结晶相中分子基团局部运动明显提升;非晶/结晶界面相中分子运动变化较为复杂——非晶/结晶界面相中靠近非晶相的分子链运动速度明显提升,而靠近结晶相的分子链运动的速度提升表现不明显;非晶相的分子链在观测温度范围内一直处于快速运动状态.
基于对各个相结构中分子链运动的认识,本文进一步研究和探讨了通过宽线固体1H NMR谱中各信号成分测量样品结晶度的可行性.结果发现,宽线固体1H NMR谱中各信号成分的含量与材料的结晶度并不存在直接的关系,其主要原因可能是由于非晶/结晶界面相中分子链具有复杂的构象序列.
| [1] | BASSETT D C. Principles of polymer morphology[M]. Cambridge University Press, 1981. |
| [2] | HORⅡ F, KITAMARU R. Refined NMR analysis of the phase structure of solutioncrystallized linear polyethylene[J]. J Polym Sci Pol Phys, 1978, 16(2): 265-270. DOI: 10.1002/pol.1978.180160207. |
| [3] | KITAMARU R, HORⅡ F, MURAYAMA K. Phase structure of lamellar crystalline polyethylene by solid-state high-resolution carbon-13 NMR detection of the crystalline-amorphous interphase[J]. Macromolecules, 1986, 19(3): 636-643. DOI: 10.1021/ma00157a026. |
| [4] | CHENG J, FONE M, REDDY V N, et al. Identification and quantitative analysis of the intermediate phase in a linear highdensity polyethylene[J]. J Polym Sci Pol Phys, 1994, 32(16): 2683-2693. DOI: 10.1002/polb.1994.090321614. |
| [5] | HASHIMOTO T, SHIBAYAMA M, KAWAI H. Domain-boundary structure of styrene-isoprene block copolymer films cast from solution. 4. molecular-weight dependence of Lamellar microdomains[J]. Macromolecules, 1980, 13(5): 1237-1247. DOI: 10.1021/ma60077a040. |
| [6] | MCBRIERTY V J, DOUGLASS D C. Recent advances in the NMR of solid polymers[J]. J Polym Sci Macromol Rev, 1981, 16(1): 295-366. DOI: 10.1002/pol.1981.230160105. |
| [7] | EDDY W. H, PER E K, PEDERSEN B. Crystallinity of polyethylene derived from solid-state proton NMR free induction decay[J]. J Phys Chem B, 1998, 102(28): 5444-5450. DOI: 10.1021/jp981753z. |
| [8] | CHEN Y, YANG G, CHEN Q. Solid-state NMR study on the structure and mobility of the noncrystalline region of poly(3-hydroxybutyrate) and poly(3-hydroxybutyrate-co-3-hydroxyvalerate)[J]. Polymer, 2002, 43(7): 2095-2099. DOI: 10.1016/S0032-3861(01)00792-3. |
| [9] | TANAKA H, NISHI T. Study of block copolymer interface by pulsed NMR[J]. J Chem Phys, 1985, 82(9): 4326-4331. DOI: 10.1063/1.448824. |
| [10] | ABRAGAM A, HEBEL L C. The principles of nuclear magnetism[M]. 1961: 56-58. |
| [11] | LOOK D C, LOWE I J, NORTHBY J A. Nuclear magnetic resonance study of molecular motions in solid hydrogen sulfide[J]. J Chem Phys, 1966, 44(9): 3441-3452. DOI: 10.1063/1.1727249. |
| [12] | ENGELSBERG M, LOWE I J. Free-inducation-decay measurements and determination of moments in CaF2[J]. Phys Rev B, 1974, 10(3): 822-832. DOI: 10.1103/PhysRevB.10.822. |
| [13] | KLÜVER W, RULAND W. NMR-studies of semicrystalline polymers using pulse techniques[M]. Steinkopff, 1978. |
| [14] | BERGMANN K, SCHMIEDBERGER H. A rapid method for the NMR-measurement of two-phase polymers[J]. Colloid Polym Sci, 1980, 258(1): 24-26. DOI: 10.1007/BF01474950. |
| [15] | DADAYLI D, HARRIS R K, KENWRIGHT A M, et al. Solid-state 1H n.m.r. studies of polypropylene[J]. Polymer, 1994, 35(19): 4083-4087. DOI: 10.1016/0032-3861(94)90579-7. |
| [16] | KRISTIANSEN P E, HANSEN E W, PEDERSEN B. Phase distribution in polyethylene versus temperature probed by solid-state proton NMR free induction decay[J]. Polymer, 2000, 41(1): 311-321. DOI: 10.1016/S0032-3861(99)00091-9. |
| [17] | PER E K, AND E W H, PEDERSEN B. Phase distribution during isothermal crystallization of polyethylene probed by solid-state proton NMR free induction decay[J]. J Phys Chem B, 1999, 103(18): 3552-3558. DOI: 10.1021/jp984539j. |
| [18] | JAEGER C, HEMMANN F. EASY:a simple tool for simultaneously removing background, deadtime and acoustic ringing in quantitative NMR spectroscopy——part Ⅰ:basic principle and applications[J]. Solid State Nucl Magn Reson, 2014, 57-58(1): 22-28. |
| [19] | HUANG Z J, JIANG J, SHI L Y, et al. Dependences of confining size and interfacial curvature on the glass transition of polydimethylsiloxane in self-ssembled block copolymers[J]. Macromol Chem Phys, 2018, 219(3): 1700518. DOI: 10.1002/macp.201700518. |
| [20] | TENG C, XUE G. Unjamming transition and cold flow of polymer chains[J]. Acta Polym Sin, 2011, 11(9): 1001-1006. DOI: 10.3724/SP.J.1105.2011.11123. |
| [21] | ZHU L L, WANG X L, GU Q, et al. Effects of residual surfactant on the glass transition behavior of polystyrene/gold nanocomposites[J]. Polymer, 2015, 77: 14-20. DOI: 10.1016/j.polymer.2015.09.013. |
| [22] | XIAO T, YAO Y F. Local and collective chain motions in semi-crystalline polyethylene-a solid-state NMR approach[J]. Chinese J Magn Reson, 2015, 32(2): 208-227. |
| [23] |
JIANG T T, FU X B, WU J Z, et al. Structure and dynamics in the polymer-ceramic interface of Li1.5Al0.5G1.5P3O12/polyether solid electrolyte:A solid state NMR study[J].
Chinese J Magn Reson, 2017, 34(4): 429-438.
姜婷婷, 付晓彬, 吴金泽, 等. Li1.5Al0.5Ge1.5P3O12/高分子固体电解质表界面结构与分子运动的固体NMR研究[J]. 波谱学杂志, 2017, 34(4): 429-438. |
| [24] | UEHARA H, KOMOTO T, YAMANOBE T. Relationship between solid-state molecular motion and morphology for ultrahigh molecular weight polyethylene crystallized under different conditions[J]. Macromolecules, 2000, 33(13): 4861-4870. DOI: 10.1021/ma9918957. |
| [25] | RASTOGI S, YAO Y, RONCA S, et al. Unprecedented high-modulus high-strength tapes and films of ultrahigh molecular weight polyethylene via solvent-free route[J]. Macromolecules, 2011, 44(14): 5558-5568. DOI: 10.1021/ma200667m. |
| [26] | YAO Y F, RASTOGI S, XUE H J, et al. Segmental mobility in the noncrystalline regions of nascent polyethylene synthesized using two different catalytic systems with implications on solid-state deformation[J]. Polymer, 2013, 54(1): 411-422. DOI: 10.1016/j.polymer.2012.11.002. |
 2019, Vol. 36
2019, Vol. 36 
