引言

基于扩散磁共振成像（Diffusion Magnetic Resonance Imaging，dMRI）的纤维追踪（Fiber Tracking，FT）技术是目前唯一能够在活体内无创地重建脑部神经纤维解剖结构的技术，能够帮助临床医生诊断及治疗神经退行性疾病，具有重要的临床意义^[1].扩散张量成像（Diffusion Tensor Imaging，DTI）是最常用的dMRI建模方法，它基于脑白质中水分子的运动服从高斯分布的假设，只能描述体素内单纤维结构，而无法描述多纤维交叉、分支等复杂的情况^{[2, 3]}.近年来，高角度分辨率扩散成像（High Angular Resolution Diffusion Imaging，HARDI）因具有能够重建白质内多纤维结构的优点引起研究者的关注^[4-6]，包括扩散谱成像（Diffusion Spectrum Imaging，DSI）、Q-ball成像（Q-Ball Imaging，QBI）、球面反卷积（Spherical Deconvolution，SD）、高阶张量模型（High Order Tensor model，HOT）、多张量模型（Multi-Tensor Model，MTM）等.其中，SD模型因其利用临床上可行采集时间内获得的数据可靠地重建神经纤维的能力，得到了广泛的应用^[7].

SD模型利用卷积关系直接从dMRI数据中重建纤维方向分布函数（Orientation Distribution Function，ODF），对噪声极其敏感.根据不同的基函数表示、正则化策略以及卷积核函数表示，研究者们提出了许多基于SD的模型^{[8, 9]}.在不同的SD模型中，约束球面反卷积（Constrained Spherical Deconvolution，CSD）模型由于在ODF估计中表现出较好的角度分辨率和较高的计算效率，成为研究热点^{[10, 11]}.由于实际测量的dMRI数据中通常存在噪声，重建得到的ODF存在负值，CSD采用Tikhonov正则化技术来保证ODF的非负性^[12].然而传统的CSD利用整数阶正则化，在ODF估计中对信号数据进行了滤波处理，可能会丢失某些细节信息^[13]，从而导致基于此模型追踪得到的纤维束不准确.研究发现，利用分数阶正则化可以弥补这一缺点^{[14, 15]}.同时，根据解剖学理论，脑白质神经纤维束有一定的平滑性和连续性，通过空间一致性正则化将体素邻域信息引入ODF重建框架中可以提高ODF的平滑度^{[16, 17]}，进而改善ODF的重建精度.

本文提出一种非局部CSD（Non-Local CSD，NLCSD）模型，结合邻域信息和分数阶正则化对传统CSD模型进行了改进.FT技术是唯一能获得关于体内白质结构连接性信息的非侵入性工具^{[18, 19]}，为了研究本文提出的NLCSD模型在纤维追踪方面的效能，我们对脑白质神经纤维进行追踪实验，并分别利用模拟数据和实际数据对基于NLCSD模型和传统CSD模型的FT结果进行了定性分析和定量分析的对比.

1 CSD模型 1.1 传统CSD模型

SD模型^[20]可以用来计算每个成像体素内的ODF.dMRI信号可以表示为卷积核函数、响应函数（Response Function，RF）和ODF在球形坐标系上的卷积，用$R(\theta )$表示RF，用$F(\theta , $$\phi )$表示ODF，卷积关系表示为：

$ \frac{S(\theta , \phi ）}{{S}_{0}}={\displaystyle {\int }_{{S}^{2}}F(\theta , \phi )\cdot R(\theta )\rm{d}}\theta \rm{=}F(\theta , \phi )\otimes R(\theta )$

(1)

其中，${S_{\rm{0}}}$表示在没有扩散敏感梯度下的dMRI信号，${S^2}$为单位球域，$(\theta , \phi )$表示球面坐标系中的方向.

球谐（Spherical Harmonics，SH）基作为球面上的完备正交基，可用来表示球体上的任何有界的单值函数.在SH框架内^[12]，对于阶数$l$，$ \frac{S(\theta , \phi ）}{{S}_{0}}$和$F(\theta , \phi )$可写成长为${\rm{(2}}l{\rm{ + 1)}}$的向量${s_l}$和${f_l}$，$R(\theta )$可写成大小为$({\rm{2}}l + 1) \times (2l + 1)$的矩阵${R_l}$，(1)式的卷积运算可以简单地表示为矩阵乘法运算：

${s_l} = {R_l} \cdot {f_l}$

(2)

根据(2)式，ODF可通过矩阵的反卷积运算求解得到，其求解可转化为标准最小二乘法估计问题，

$f = \arg \min \left\{ {||Af - s|{|^2}} \right\}$

(3)

其中，$f$对应ODF的SH系数；$s$对应dMRI信号强度；矩阵$A = B \cdot R$，B为ODF的SH系数与ODF的映射函数，R为响应核函数.

然而，正如大多数求逆问题一样，SD模型的求解过程是病态的，且容易受到噪声的影响.为了减少该技术的不适定性，Tournier等^[12]提出使用Tikhonov正则化对ODF的负值施加约束，称为CSD模型.此时，ODF可由带约束项的最小二乘法估计求得，即Tikhonov正则化，表示为：

$f = \arg \min \left\{ {||Af - s|{|^2} + {\lambda ^2}||Lf|{|^2}} \right\}$

(4)

其对应的Euler方程为：

$({A^T}A + \lambda {L^T}L)f = {A^T}s$

(5)

上式中，L表示Tikhonov矩阵，一般情况下，用单位矩阵I表示；λ（λ > 0）为正则化参数.

然而，通过(5)式得到的模型解过于光滑，可能缺失很多细节信息，这是因为矩阵${A^T}$类似一个低通滤波，在执行${A^T}s$运算时，信号s中的某些细节可能被平滑，而且这些细节无法恢复^[13].

1.2 NLCSD模型

为了减少Tikhonov正则化中模型解过于光滑的问题，使得模型解更逼近真实解，且为了提高模型重建的抗噪性及鲁棒性，在传统CSD模型的基础上，本文提出一种结合邻域信息和分数阶正则化的非局部CSD模型——NLCSD，进行ODF的估计.Tikhonov正则化的一个有效变体是分数阶Tikhonov方法，由于分数阶的本质特性是非局部的，分数阶正则化使得模型重建的细节信息相对较好，减少过度光滑现象的发生^[21].该方法用加权的最小二乘法对模型求解，表示为：

$f = \arg \min \left\{ {||Af - s||_W^2 + {\lambda ^2}||Lf|{|^2}} \right\}$

(6)

其中，$||x|{|_W} = {({x^T}Wx)^{1/2}}$，W为半正定对称矩阵，表示为：

$W = {(A{A^T})^{(\alpha - 1)/2}}$

(7)

则Tikhonov最小化问题(6)式对应的Euler公式为：

$[{({A^T}A)^{(\alpha + 1)/2}} + \lambda {L^T}L]f = {({A^T}A)^{(\alpha - 1)/2}}{A^T}s$

(8)

由于噪声会对ODF重建的精度产生影响，特别是在纤维交叉等复杂区域，ODF会变得紊乱，导致在该ODF基础上追踪得到的纤维不连续且不准确，然而，解剖学上白质纤维束具有空间平滑性，因此基于空间正则化将体素邻域信息引入ODF重建框架可以减少噪声的影响^[22].

采用加权2范数正则化的方法引入相邻体素中的信息对ODF重建模型进行约束处理.从邻域体素纤维的ODF约束和信号约束出发，重新定义(4)式

$f = \arg \min \left\{ {||Af - s|{|^2} + {\alpha _{\rm{1}}}^{\rm{2}}\sum\limits_{i = 1}^n {{\beta _i}||Bf - B{f_i}|{|^2} + } {\alpha _2}^{\rm{2}}\sum\limits_{i = 1}^n {{\beta _i}||Af - {s_i}|{|^2} + } {\lambda ^2}||Lf|{|^2}} \right\}$

(9)

其中，$ {\alpha }_{\rm{1}}、{\alpha }_{\rm{2}}$是平衡两个约束项的权重，${f_i}(i = 1, 2, 3, \cdots )$为邻域体素内ODF的SH系数，${s_i}(i = 1, 2, 3, \cdots )$为邻域体素内信号数据，${\beta _i}(i = 1, 2, 3, \cdots )$为相邻两体素之间的相似度，我们采用体素的26-邻域信息施加空间正则化约束.

根据矩阵2范数的性质，(9)式可表达为：

$f = \arg \min \left\{ {{{\left\| {\left( {\begin{array}{*{20}{c}} A \\ {{\alpha _1}J} \\ {{\alpha _2}P} \end{array}} \right)f - \left( {\begin{array}{*{20}{c}} s \\ {{\alpha _1}K} \\ {{\alpha _2}Q} \end{array}} \right)} \right\|}^2} + {\lambda ^2}{{\left\| {Lf} \right\|}^2}} \right\}$

(10)

其中，J、K、P、Q表示为：

$J = \left( {\begin{array}{*{20}{c}} {\sqrt {{\beta _1}} B} \\ {\sqrt {{\beta _2}} B} \\ \vdots \\ {\sqrt {{\beta _n}} B} \end{array}} \right), {\rm{ }}K = \left( {\begin{array}{*{20}{c}} {\sqrt {{\beta _1}} B{f_1}} \\ {\sqrt {{\beta _2}} B{f_2}} \\ \vdots \\ {\sqrt {{\beta _n}} B{f_n}} \end{array}} \right), {\rm{ }}P = \left( {\begin{array}{*{20}{c}} {\sqrt {{\beta _1}} A} \\ {\sqrt {{\beta _2}} A} \\ \vdots \\ {\sqrt {{\beta _n}} A} \end{array}} \right), {\rm{ }}Q = \left( {\begin{array}{*{20}{c}} {{s_1}} \\ {{s_2}} \\ \vdots \\ {{s_n}} \end{array}} \right)$

(11)

用Euler公式表示(10)式：

$({A^T}A + {\alpha _{\rm{1}}}{J^T}J + {\alpha _2}{P^T}P + \lambda {L^T}L)f = {A^T}s + {\alpha _{\rm{1}}}{J^T}K + {\alpha _2}{P^T}Q$

(12)

引入分数阶Tikhonov方法理论，根据(8)式、(11)式和(12)式可求得

$f = {\left[ {{{({A^T}A)}^{(\alpha + 1)/2}} + {\alpha _{\rm{1}}}{J^T}J + {\alpha _2}{P^T}P + \lambda {L^T}L} \right]^{ - 1}}\left[ {{{({A^T}A)}^{(\alpha - 1)/2}}{A^T}s + {\alpha _{\rm{1}}}{J^T}K + {\alpha _2}{P^T}Q} \right]$

(13)

上述ODF重建估计算法流程框架如下所示：

2 FT技术

FT技术可以用来无创地重构大脑白质神经纤维束，根据ODF我们可以估计白质组织的性质并提取出白质组织的结构走向，基于这些走向采用确定型追踪算法可以观察白质组织的微观结构，实现神经纤维束的三维重构.在数学上，确定型追踪算法可看作常微分初值问题，其基本思想是沿着纤维模型估计的主要方向追踪白质组织的轨迹路径^[23]，定义$x(t)$为三维空间坐标系中的纤维束轨迹：$t \to x(t)$、$\mathbb{R} \to \mathbb{R}$³，则

$\left\{ \begin{array}{*{20}{l}} \frac{{{\rm{d}}x(t)}}{{{\rm{d}}t}} = e[x(t)] \\ x(0) = {x_0} \\ \end{array} \right.$

(14)

其中，$e$表示纤维轨迹$x(t)$在$t$处的特征走向，${x_0}$为纤维轨迹的种子点，采用Euler法对(14)式求解，一条新的纤维路径可通过(15)式递推得到，

${x_{t + 1}} = {x_t} + \mu {d_t}$

(15)

其中，$\mu > 0$为行进步长，${d_t}$为当前t点追踪的方向.${d_t}$定义为最邻近峰值方向，选取与前一步方向余弦相似度最大的峰值作为当前点的行进方向，其余弦相似度$\theta $由点积和向量长度给出，表示为：

$\cos (\theta ) = \frac{{{\varepsilon _t} \cdot {d_{t - 1}}}}{{\left\| {{\varepsilon _t}} \right\|\left\| {{d_{t - 1}}} \right\|}}$

(16)

${d_t} = {\varepsilon _t}\left\{ {\max \left[ {\cos (\theta )} \right]} \right\}$

(17)

其中${\varepsilon _t} = [{\varepsilon _{t1}}, {\varepsilon _{t2}}, \ldots ]$，为${x_t}$处体素的峰值方向.FT路径递推可由图 1表示，在${x_2}$处选择与${d_1}$余弦相似度最大的${\varepsilon _{{\rm{2}}2}}$作为当前点的追踪方向.

此外，为了准确追踪，需要设置停止准则，一般当局部各向异性或曲率低于预定阈值时终止FT^[24]. FT算法流程如下所示：

3 实验结果与讨论

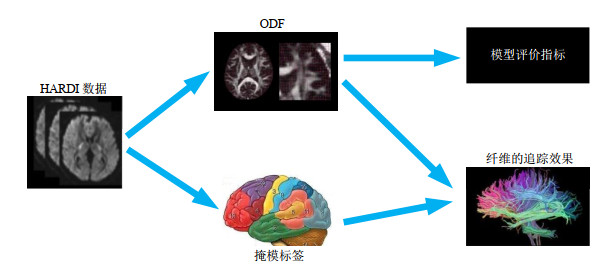
为了验证本文算法的有效性，以Python为平台，对基于本文提出的NLCSD模型与传统CSD模型的FT算法作对比实验，实验流程如图 2所示，实验利用模拟数据和实际数据分别ODF重建和纤维的追踪效果两个部分进行定性分析和定量分析.

3.1 模拟数据

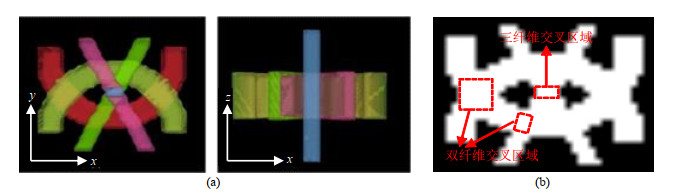
本实验所用模拟数据为Ye等^[17]所设计的三维数字交叉模型，该数据模拟了纤维交叉和弯曲等纤维结构，如图 3所示，包含60个扩散敏感梯度方向和一个未加权敏感梯度的图像，扩散敏感梯度设置为1 000 s/mm²，包含50×50×50个体素数据，信噪比（Signal to Noise Ratio，SNR）包含10、20和30三种.

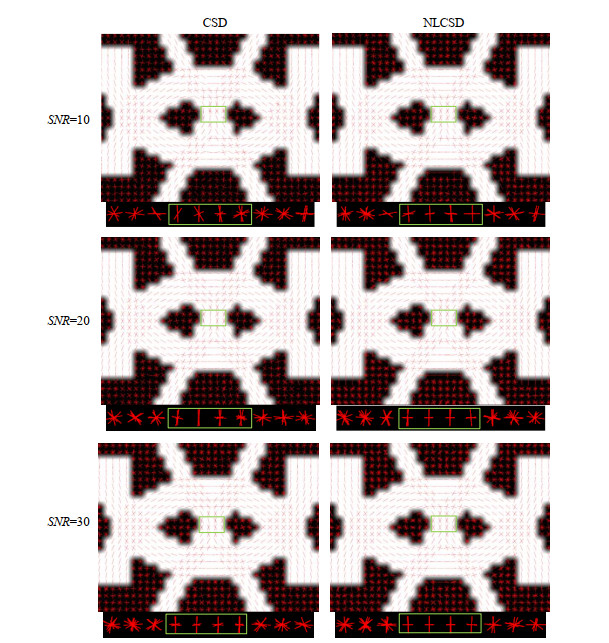
我们分别采用NLCSD模型和CSD模型对该合成数据进行ODF重建，纤维在每个体素的走向用ODF的峰值来表示，追踪算法利用这些峰值描述大脑的连通性.为了更清晰的比较两种模型对于ODF重建结果的好坏，我们根据ODF，对体素的峰值进行显示，重建结果如图 4和图 5所示，第二行为绿色框内体素在OXZ平面内的视角.从整体视觉效果看，NLCSD模型重建的结果更加的整洁、一致，而CSD模型较紊乱；针对纤维交叉区域，NLCSD模型能更准确的对交叉结构的体素扩散模型进行重建；同时对于含有三根纤维交叉的体素区域，NLCSD模型能更完整、准确地重建出三个峰值.

同时，我们在ODF重建基础上，设置50个种子点，采用FT算法对该模拟数据进行纤维的追踪，追踪结果如图 6所示，从图中可以看出，在SNR为10和20的情况下，基于CSD模型的FT算法出现了很多错误的追踪结果，而基于NLCSD模型的FT算法得到的追踪结果较准确；在SNR为30的情况下，两种算法都没有出现错误的追踪结果.与基于CSD模型的追踪算法相比，基于NLCSD模型的追踪算法追踪得到的纤维束更加完整，更符合实际的纤维束结构.

为了进一步说明本文算法的可靠性，我们对ODF重建结果以及纤维的追踪结果进行定量评价.通过估计纤维交叉区域的平均交叉角度评价ODF的重建精度^[25]，本文实验只针对两条线性结构在OXZ平面内的纤维交叉情况进行角度误差分析，即图 3(b)中三纤维交叉区域内的体素，其实际角度为90˚，ODF峰值的交叉角度估计可表示为(18)式：

$angl{e_i} = cross({\mu _{i, 1}}, {\mu _{i, {\rm{2}}}})$

(18)

其中，$ {\mu }_{i, 1}、{\mu }_{i, 2}$为体素$i$处的两个峰值方向，$i = (1, 2, \cdots , N)$，N为参与角度误差分析的体素个数，由于每个体素存在两个交叉峰值，其角度估计取两个交叉角度的平均值.对交叉角度的标准差（Standard Deviations，SD）以及均方根误差（Root Mean Square Error，RMSE）估计，表示为(19)式和(20)式，结果如图 7所示，从图中可以看出，使用NLCSD重建得到的ODF角度误差更小，准确度也更高.随着SNR的提高，两种模型之间的差距逐渐缩小.

$SD = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{[angl{e_i} - \frac{1}{N}(\sum\limits_{i = 1}^N {angl{e_i}} )]}^2}} }}{N}} $

(19)

$RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{(angl{e_i} - angl{e_{true}})}^2}} }}{N}} $

(20)

其中，$angl{e_{true}}$为实际交叉角度.

针对纤维的追踪结果，我们定义纤维追踪的识别率作为定量评价的指标，实际的纤维数量为N（N=50），正确追踪的纤维数量为RN，错误追踪的纤维数量为WN，不完整追踪的纤维数量为ICN，分析结果如表 1所示，从表 1可以看出相比于CSD模型，基于NLCSD模型追踪的纤维更加完整，准确追踪的纤维数量更多，错误追踪的纤维数量更少.

3.2 实际数据

本实验使用的实际人脑数据来自斯坦福大学数据资料库^[26]，由GE 3T MRI扫描设备扫描得到，扫描采用的参数为：分辨率为2×2×2 mm³，体素量为81×106×76，扩散敏感系数为2 000 s/mm²，采用150个扩散敏感梯度方向以及10个未施加敏感梯度的扫描图像.

选取多处单纤维体素感兴趣区域以及多纤维交叉体素区域，采用两种模型进行ODF重建（图 8）.由图 8可知，对于单纤维区域，使用NLCSD模型得到的ODF走向具有一致性、平滑性，而CSD模型重建结果不仅紊乱，而且存在伪峰；对于多纤维交叉区域，与CSD模型相比，NLCSD模型重建得到的ODF更准确、平滑，重建精度相对较高.

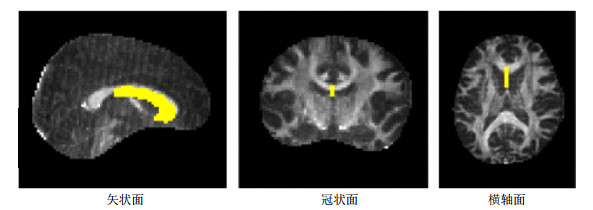
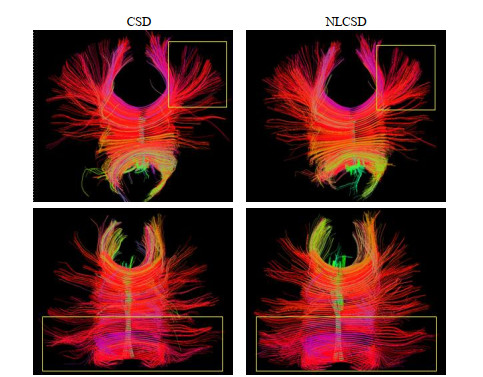
同时，在该ODF基础上对胼胝体部分区域进行FT实验，种子点区域设置如图 9所示，实验结果如图 10所示，实验结果表明，基于CSD模型的FT算法追踪的纤维比较稀疏，而基于NLCSD模型的FT算法追踪得到的纤维轨迹可以更广泛的向皮层分散.

为了验证本文算法的优越性，我们从追踪的纤维数量和纤维长度两方面对两种算法进行定量评价^[27].基于NLCSD模型的FT算法得到的纤维数量为77.82×50条、平均长度为80.62 mm，优于CSD模型（纤维数量为76.80×50条，平均长度为60.58 mm）.

为了分析NLCSD模型的时间效率，使用两种算法对等体素量的数据进行ODF重建实验：分别选取20×20×20、30×30×30和40×40×40的体素量，所用设备为Intel(R) Core(TM) i5-8400 CPU @2.80GHz 2.81GHz，分别进行两次试验取其平均值，两种算法的时间效率分析如表 2所示.从表 2可以看出，NLCSD模型的重建时间较长，这是由于NLCSD模型在ODF建模的过程中，对体素的邻域方向信息进行估计并添加约束计算.

4 结论

FT的准确性依赖于ODF的精度，针对SD模型中存在的不适定性问题，本文在传统CSD模型的基础上，提出了一种结合体素邻域信息和分数阶正则化的NLCSD模型，并完整阐述了基于NLCSD模型的确定型FT技术，对脑白质神经纤维进行ODF重建以及纤维三维追踪.通过对NLCSD模型以及CSD模型进行对比实验，验证了NLCSD模型的可靠性.实验结果表明：相对于CSD模型的重建结果具有一定的紊乱性，NLCSD模型得到的ODF更加清晰、视觉效果较好；同时对于具有多根纤维交叉的体素，NLCSD模型能更完整地重建出多个峰值.从纤维的追踪结果看，基于NLCSD模型的FT算法能够更准确、完整地追踪出纤维交叉等结构.但是NLCSD模型对于小角度的识别效果不佳，同时本文仅采用简单的确定性追踪，仍存在方向误差累积问题，之后可以进一步改进模型重建算法，提高小角度纤维交叉的重建结果，同时寻求一种更精确的非局部FT技术以减少误差累积问题.