2. 上海市第一人民医院 泌尿外科, 上海 200080
2. Department of Urology, Shanghai First People's Hospital, Shanghai 200080, China
近年来,随着人们生活水平的提高,前列腺癌的发病率和死亡率越来越高[1],是位居欧美国家男性发病率第一位、死亡率第二位的恶性肿瘤.2018年,中国国家癌症中心[2]发布的我国肿瘤登记地区表明我国前列腺发病率也有明显的增长趋势,上海、北京、广州发达城市的发病率已经达到了0.01%.临床经验表明,前列腺癌如果能尽早发现并及时治疗,会大大提高患者的生存率.医学影像在前列腺癌诊断和治疗中发挥着重要作用.其中磁共振图像对组织分辨率高,具有多方向、多参数成像方式,不仅能显示人体解剖结构及其病理变化的信息,而且还能提供有关器官的功能信息.而图像分割[3]是基于磁共振图像的前列腺癌早期诊断和治疗的基础[4, 5].
几何活动轮廓模型是图像分割领域的重要研究方向之一[6-13].2010年,Langerak等[14]利用标记融合方法进行了前列腺磁共振图像分割研究.该方法首先将目标图像与训练图像库中的多幅图像进行配准,然后将配准后的训练图像进行手工分割,配准的质量直接影响分割结果.2010年,Gao等[15]利用形状配准方法进行了前列腺磁共振图像分割研究.该方法基于面配准,而点相关信息的缺乏导致基于面配准算法必须建立在迭代搜索的基础上,占用机时长.2010年,Martin等[16]利用概率统计方法进行了前列腺磁共振图像分割研究.该方法在多个统计形状模型中选择最优模型,最优模型的选取直接影响图像的分割结果.2013年,Khalvati等[17]对双向配准方法进行了研究.该方法需要选取特征点,但特征点的选取较为困难,且直接影响图像分割结果.综上所述,由于前列腺磁共振图像的周围组织结构复杂,图像比较模糊而且噪声比较大,其分割一直都是一个挑战.
本文基于改进边缘的距离正则化水平集演化(Distance Regularized Level Set Evolution,DRLSE)[18]模型,对前列腺磁共振图像分阶段分割法进行了研究.相比其他水平集模型(如CV[19]、LBF[20]等),该方法提高了分割精度,而且操作简单,可以直接对现有图像进行处理.本文还并采用Dice相似性系数(Dice similarity coefficient,DSC)和Hausdorff距离对其分割效果进行评估.
1 改进的DRLSE模型本文提出的改进DRLSE模型是在传统DRLSE方法[21]的基础上使用两个指示函数,另外添加局部灰度信息的方法.
1.1 传统的DRLSE方法初始化函数-取点连线法在前列腺磁共振图像内部任意取N个点,使其首尾连接成为一个封闭的区域,设为
| $ {\phi }_{0}(x, y)\left\{ {\begin{array}{*{20}{l}}-{c}_{0}, \ \ \ \ \ \ {\phi }_{0}(x, y)\in {S}_{N}\\ {c}_{0}, \ \ \ \ \ \ \ \ \ \ 其它\end{array}} \right.$ | (1) |
为了解决水平集函数在演化过程中需要不断初始化为符号距离函数的问题,Li提出了DRLSE方法[21],在传统的活动轮廓模型中的能量泛函上再添加一项内部能量泛函,该方法可以来纠正水平集函数在演化过程中与距离函数的偏差,从而实现水平集函数在演化过程中无需周期性地重新初始化水平集函数的要求,其能量泛函如(2)式所示:
| $\varepsilon (\phi ) = \mu {R_p}(\phi ) + {\varepsilon _{ext}}(\phi )$ | (2) |
其中
内部能量泛函
| ${R_p}(\phi ) = \mu \int_\mathit{\Omega} {p(|\nabla \phi |){\rm{d}}x} $ | (3) |
(3) 式为函数ϕ的内部能量泛函(Ω是图像的区域),用于消除水平集函数和符号距离函数之间的偏差,使其始终保持符号距离函数的属性;
| $p(s)\left\{ {\begin{array}{*{20}{l}} \frac{1}{{{{(2\pi )}^2}}}[1 - \cos (2\pi s)], \ \ \ s \leqslant 1 \\ \frac{{{{(s - 1)}^2}}}{2}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ s > 1 \\ \end{array}} \right.$ | (4) |
| ${\varepsilon _{ext}}(\phi ) = \lambda {L_g}(\phi ) + \alpha {A_g}(\phi ) = \lambda \int_\mathit{\Omega} {g{\delta _\varepsilon }(\phi )(|\nabla \phi |){\rm{d}}x + \alpha } \int_\mathit{\Omega} {g{H_\varepsilon }( - \phi ){\rm{d}}x} $ | (5) |
其中ϕ为水平集函数.
| $ {H_\varepsilon } = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}\left[ {1 + \frac{x}{\varepsilon } + \frac{1}{{\pi}}\cos \left( {\frac{{{\pi}x}}{\varepsilon }} \right)} \right], }&{\left| x \right| \leqslant \varepsilon } \\ {0, }&{x > \varepsilon } \\ {0, }&{x < - \varepsilon } \end{array}} \right. $ | (6) |
| ${\delta _\varepsilon } = \left\{ {\begin{array}{*{20}{l}} \frac{1}{{2\varepsilon }}\left[ {1 - \sin (\frac{{{\rm{ \mathsf{ π} }}x}}{\varepsilon })} \right], \ \ \ |x| \leqslant \varepsilon \\ 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x| > \varepsilon \\ \end{array}} \right.$ | (7) |
g为边界指示函数.本文首先观察了在传统DRLSE下使用两个边界函数进行前列腺图像分割的情况.前一阶段使用
| $ {g_1}(x, y) = \frac{1}{{1 + |\nabla {G_{{\sigma _1}}}I(x, y){|^2}}} $ | (8) |
(8)式中
| ${g_2}(x, y) = \rho {{\rm{e}}^{ - \frac{{|\nabla {G_{{\sigma _2}}}I(x, y){|^2}}}{{2{\sigma _2}^2}}}}$ | (9) |
ρ表示权重参数.
对于磁共振图像,特别是对前列腺磁共振图像来说,由于前列腺靠近膀胱一侧的边界比较模糊,对比度比较低,传统DRLSE模型中的停止函数无法准确定位弱边界[22],容易导致过分割.改进的径向基高斯核函数为边缘停止函数[23],该函数满足单调性,自变量趋向于∞时,函数值趋近0;自变量趋向于0时,函数值趋近于ρ,使曲线在前列腺弱边界处停止演化.通过最小化泛函能量函数
| $ \frac{{\partial \phi }}{{\partial t}} = \mu div({d_p}|\nabla \phi |\nabla \phi ) + \lambda {\delta _\varepsilon }(\phi )div(g\frac{{|\nabla \phi |}}{{\nabla \phi }}) + \alpha g{\delta _\varepsilon }(\phi ) $ | (10) |
其中∇为拉普拉斯算子;div为散度.
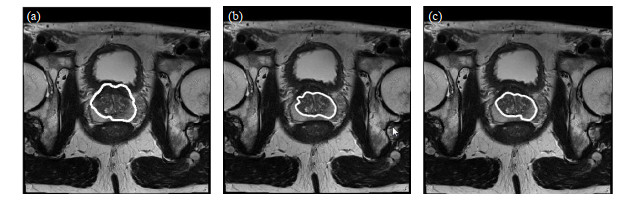
图 1为传统DRLSE下使用不同指示函数的演化结果.由图像分割结果可见,图 1(a)前列腺靠近膀胱一侧梯度不明显,仅使用
|
图 1 基于传统DRLSE,使用不同指示函数对前列腺磁共振图像进行分割.(a)仅使用g1(I);(b)仅使用g2(I);(c)使用g1(I)和g2(I)分阶段演化 Fig. 1 With the traditional DRLSE, different indicator functions are used to segment the prostate magnetic resonance images. (a) Only use g1(I); (b) Only use g2(I); (c) Phased evolution using g1(I) and g2(I) |
鉴于传统DRLSE方法在前列腺轮廓提取方面的局限,本文从局部灰度信息出发对其进行改进.即在传统DRLSE的外部能量泛函中添加新的能量项,本文称之为牵制能量项
| ${E_{ext}}(\phi ) = \lambda {L_g}(\phi ) + \alpha {A_g}(\phi ) + k{C_g}(\phi )$ | (11) |
其中,k为牵制能量项的权重系数.牵制能量项为(12)式所示:
| ${C_g} = \int_l {XH} ( - \phi ){\rm{d}}x$ | (12) |
| $X = 1/\sum\nolimits_1^n | {f_j} - {f_i}|$ | (13) |
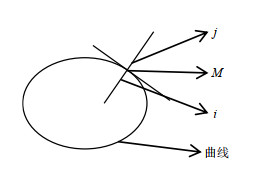
其中,n为水平集曲线上选取的点的个数,以选取的点M作曲线的法线,在M点的法线上选取位于曲线两侧的点i和j(图 2),
| ${E_{ext}}(\phi ) = k{C_g}(\phi )$ | (14) |
|
图 2 曲线内外点像素的示意图 Fig. 2 Schematic diagram of point pixels inside and outside the curve |
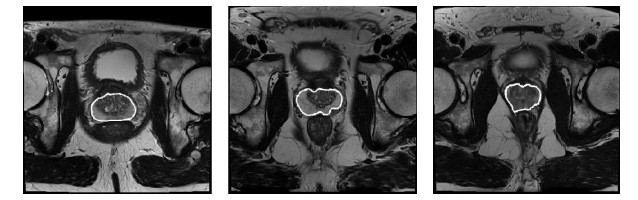
外部能量仅使用牵制能量项泛函进行演化的结果如图 3所示.结果显示,使用能量牵制项可以使曲线向边界靠近,特别是向梯度变化比较大的地方演化,而且可加速曲线的演化.
|
图 3 使用能量牵制项演化结果.三幅图为不同扫描层的磁共振图像 Fig. 3 Use energy to constrain term evolution. The three images are from three slices |
本文改进的DRLSE方法保留了传统DRLSE的长度项和面积项,为了得到极小值,将(2)式转化为偏微分方程,如(15)式所示:
| $\frac{{\partial \phi }}{{\partial t}} = \mu div({d_p}|\nabla \phi |\nabla \phi ) + \lambda {\delta _\varepsilon }(\phi )div(g\frac{{|\nabla \phi |}}{{\nabla \phi }}) + \alpha g{\delta _\varepsilon }(\phi ) + k{C_g}{\delta _\varepsilon }(\phi )$ | (15) |
由上式可得,改进DRLSE方法不仅利用了图像边界的梯度信息,而且还利用了图像的局部灰度信息,能够拖动零水平集向边界处运动.当水平集的能量泛函最小时,牵制能量项达到最小值,曲线恰好达到边界值,此时,零水平集即为前列腺的真实轮廓.
用改进DRLSE方法对前列腺磁共振图像进行前列腺轮廓的提取,演化结果如图 4所示.

|
图 4 使用改进DRLSE方法对前列腺磁共振图像的演化结果.三幅图为不同扫描层的磁共振图像 Fig. 4 The evolutionary results for prostate magnetic resonance images using the improved DRLSE method. The three images are from three slices |
实验结果表明,改进DRLSE方法对前列腺轮廓的提取具有较好的效果,有效地解决了传统的DRLSE方法对前列腺轮廓提取所存在的问题,添加了牵制能量项来驱使曲线越过虚假边界继续演化,同时根据外部能量泛函中的长度和面积最小原则,使零水平集接近梯度极值,最终到达目标区域梯度极值处.
2 材料与方法本文选用国际光学和光子学会、美国物理学家协会和国家癌症研究所联合发起的医疗影像识别竞赛PROSTATEx数据库中190幅前列腺磁共振图像进行实验.
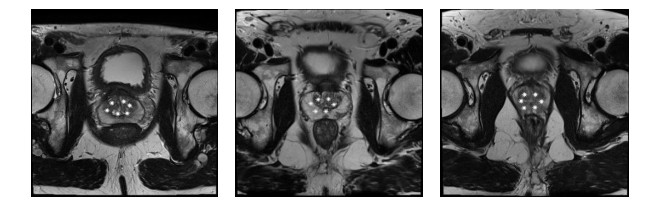
3 实验结果与分析 3.1 传统DRLSE方法和改进DRLSE方法进行前列腺磁共振图像分割的对比本文选取六个点进行初始轮廓设定,均为多边形(图 5).
|
图 5 前列腺初始轮廓设定.三幅图为不同扫描层的磁共振图像 Fig. 5 The initial outline of the prostate. The three images are from three slices |
前列腺磁共振图像分割实验在Matlab2016b下运行,其中主要参数的取值:
|
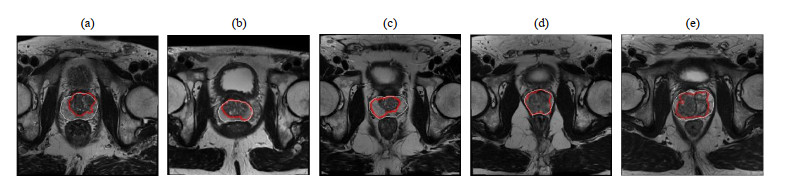
图 6 传统DRLSE方法分阶段对前列腺磁共振图像的演化结果.(a)~(e)分别为第9、10、11、12、13层扫描层轮廓 Fig. 6 The results of prostate magnetic resonance images using two-stage evolution by traditional DRLSE method. (a)~(e) are the 9th~13th slices, respectively |
|
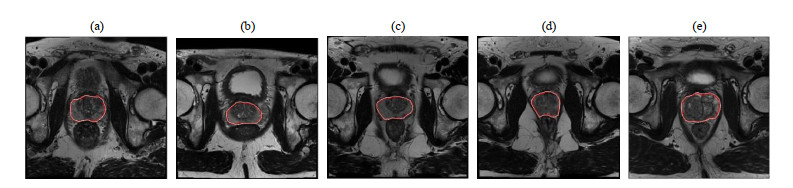
图 7 改进DRLSE方法分阶段对前列腺磁共振图像的演化结果.(a)~(e)分别为第9、10、11、12、13层扫描层轮廓 Fig. 7 The results of prostate magnetic resonance images using two-stage evolution by improved DRLSE method. (a)~(e) are the 9th~13th slices, respectively |
文献[24]提出将Hausdorff距离用于评估两条曲线之间的误差.本文将使用算法分割区域定义为像素集A,将专家手动分割的标准区域定义为像素集B.Hausdorff距离定义如(16)式和(17)式所示:
| $H(A, B) = \max (h(A, B), h(B, A))$ | (16) |
| $h(A, B) = {\max _{a \in A}}{\min _{b \in B}}||a - b||$ | (17) |
文献[25]提出使用DSC对使用的分割方法的精确性进行定量评估.DSC定义如(18)式所示:
| $DSC({A_s}, {A_m}) = 2\frac{{|{A_s} \cap {A_m}|}}{{|{A_s}| + |{A_m}|}} \times 100\% $ | (18) |
其中,
| 表 1 传统和改进DRLSE方法对前列腺磁共振图像不同扫描层轮廓提取的DSC和Hausdorff距离 Table 1 The mean DSC values and Hausdorff distances of different layers in prostate magnetic resonance images using traditional and improved DRLSE methods |
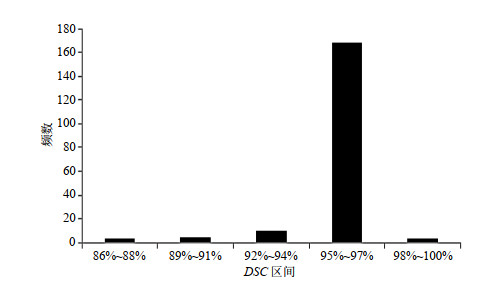
图 8为使用改进的DRLSE方法获得的190幅前列腺磁共振图像的DSC分布直方图,结果表明DSC分布集中在95%~97%区间,DSC均值为96%,可靠性较高.
|
图 8 使用改进DRLSE方法获得的190幅前列腺磁共振图像的DSC分布直方图 Fig. 8 The DSC distribution interval of 190 prostate magnetic resonance images using the improved DRLSE method |
表 2列举了文献[14-17]中使用其他方法进行前列腺磁共振图像分割获得的DSC,除双向匹配方法外,DSC值均在85%左右,使用双向匹配方法获得的DSC为92%,均小于本文提出的方法.这表明本文提出的改进DRLSE方法优于其它方法,对前列腺磁共振图像的分割效果较为理想、精度较高.
| 表 2 使用不同前列腺磁共振图像分割方法获得的DSC均值 Table 2 Comparison of mean DSC values using different prostate magnetic resonance image segmentation methods |
本文提出了一种基于改进DRLSE的前列腺磁共振图像分割方法.该方法除保留了传统DRLSE的梯度信息外,还添加了牵制能量项,并且使用了两种指示函数分阶段进行演化.由于磁共振图像比较模糊且噪声比较大,本方法在轮廓提取的过程中引入了高斯核函数,通过卷积平滑前列腺图像减少噪声,使得边界约束函数更好地促使分割算法收敛于边界,而且能越过虚假边界最终到达到真正的边界.实验结果表明,使用改进DRLSE方法对前列腺磁共振图像的分割精度明显高于传统DRLSE和文献中使用的其它方法,DSC均值可达到96%,从而证明了改进DRLSE方法对于前列腺磁共振图像分割的有效性和精确性,对前列腺疾病的临床诊断和治疗都具有非常重要的意义.
本文方法仅基于二维磁共振图像研究前列腺的分割,由于三维图像存在计算复杂等问题,对三维图像还在探索中,未来将在三维图像上展开研究.
| [1] | 韩苏军.中国前列腺癌发病及死亡现状和流行趋势分析[D].北京: 北京协和医学院, 2015. |
| [2] | CHEN W Q, SUN K X, ZHENG R S, et al. Cancer incidence and mortality in China, 2014[J]. Chinese J Cancer Res, 2018, 30(1): 1-12. DOI: 10.21147/j.issn.1000-9604.2018.01.01. |
| [3] |
WANG L J, SU X Y, LI Y, et al. Segmentation of right ventricle in cardiac cine MRI using COLLATE fusion-based multi-atlas[J].
Chinese J Magn Reson, 2018, 35(4): 407-416.
王丽嘉, 苏新宇, 李亚, 等. 基于COLLATE融合多图谱的心脏电影MRI右心室分割[J]. 波谱学杂志, 2018, 35(4): 407-416. |
| [4] | LITJENS G, TOTH R, HOEKS C, et al. Evaluation of prostate segmentation algorithms for MRI:The promise12 challenge[J]. Med Image Anal, 2014, 18(2): 359-373. DOI: 10.1016/j.media.2013.12.002. |
| [5] |
LIU K W, LIU Z L, WANG X Y, et al. Prostate cancer diagnosis based on cascaded convolutional neural networks[J].
Chinese J Magn Reson, 2020, 37(2): 152-161.
刘可文, 刘紫龙, 汪香玉, 等. 基于级联卷积神经网络的前列腺磁共振图像分类[J]. 波谱学杂志, 2020, 37(2): 152-161. |
| [6] | 刘肖.几何活动轮廓模型对灰度不均匀图像局部分割研究[D].济南: 山东大学, 2017. |
| [7] | CHAN T F, VESE L A. Active contours without edges[R]. UCLA:CAM Report, 1998:53-98. |
| [8] | ZHANG Q, LU S Q, LI H B, et al. Research on under water stereo maching method based on color segmentation[J]. Acta Optica Sinica, 2016, 36(8): 193-200. |
| [9] | SAPIRO G. Geometric partial differential equations and image analysis[M]. New York: Cambridge University Press, 2001. |
| [10] | LESTARI D P, MADENDA S, MASSICH J. A segmentation algorithm for breast lesion based on active contour model and morphological operations[J]. Advanced Science, Engineering and Medicine, 2015, 7(10): 920-924. DOI: 10.1166/asem.2015.1786. |
| [11] | LI C M, XU C Y, GUI C F, et al. Level set evoluion without re-initialization: A new variational formulation[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005: 430-436. |
| [12] | LIN Y, TONG L. Level set image segmentation of CV-GAC model[C]//201813th International Conference on Computer Science & Education (ICCSE). 2018: 1-5 |
| [13] | KHAMECHIAN M B, SAADATMAND-TARZJAN M. FoCA:A new framework of coupled geometric active contours for segmentation of 3D cardiac magnetic resonance images[J]. Magn Reson Imaging, 2018, 51: 51-60. DOI: 10.1016/j.mri.2018.04.011. |
| [14] | LANGERAK T R, VAN DER HEIDE U A, KOTE A N J, et al. Label fusion in stlas-based segmentation using a selective and iterative method for performance level estimation (SIMPLE)[J]. IEEE Trans Med Imaging, 2010, 29(12): 2000-2008. DOI: 10.1109/TMI.2010.2057442. |
| [15] | GAO Y, SANDHU R, FICHTINGER G, et al. Acouple global registration and segmentation framework with application to magnetic to magnetic resonance prostate imagery[J]. IEEE Trans Med Imaging, 2010, 29(10): 1781-1794. DOI: 10.1109/TMI.2010.2052065. |
| [16] | MARTIN S, TROCCAZ J, DAANEN V. Automated segmentation of the prostate in 3D MR images using a probabilistic atlas and a spatially constrained deformable model[J]. Med Phys, 2010, 37(4): 1579-1590. DOI: 10.1118/1.3315367. |
| [17] | KHALVAI F, SALMANPOUR A, RAHNAMAYAN S, et al. Inter-slice bidirectional registration-based segmentation of the prostate gland in MR and CT image sequences[J]. Med Phys, 2013, 40(12): 123503. DOI: 10.1118/1.4829511. |
| [18] | SELVATHI D, BAMA S. Phase based distance regularized level set for the segmentation of ultrasound kidney images[J]. Pattern Recogn Lett, 2017, 86: 9-17. DOI: 10.1016/j.patrec.2016.12.002. |
| [19] | CHAN T F, VESE L A. A level set algorithm for minimizing the Mumford-Shah functional in image processing[C]//Proceedings IEEE Workshop on Variational & Level Set Methods in computer vision, 2001: 161. |
| [20] | LI C M, KAO C Y, GORE J C, et al. Implicit active contours driven by local binary fitting energy[C]//2007 IEEE conference on Computer Vision and Pattern Recognition, 2007. |
| [21] | LI C M, XU C Y, GUI C F, et al. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Trans Image Process, 2010, 19(12): 479-488. |
| [22] | KHADIDOS A, SANCHEZ V, LI C T. Weighted level set evolution based on local edge features for medical image segmentation[J]. IEEE Trans Image Process, 2017, 26(4): 1979-1991. |
| [23] |
XU W J, WANG X. Image segmentation of thyroid nodules based on fusion KFCM and improved DRLSE model[J].
Journal of Jilin University (Science Edition), 2016, 54(5): 1124-1128.
徐文杰, 王昕. 融合KFCM与改进DRLSE模型的甲状腺结节图像分割[J]. 吉林大学学报(理学版), 2016, 54(5): 1124-1128. |
| [24] | HUTTENLOCHER D P, KLANDERMAN G A, RUCKLIDGE W A. Comparing images using the Hausdorff distance[J]. IEEE T Pattern Anal, 1993, 15(9): 850-863. DOI: 10.1109/34.232073. |
| [25] | YANG M J, LI X L, TURKBEY B, et al. Prostate segmentation in MR images using discriminant boundary features[J]. IEEE Trans Biomed Eng, 2013, 60(2): 479-488. DOI: 10.1109/TBME.2012.2228644. |
 2020, Vol. 37
2020, Vol. 37 
