2. 集美大学 理学院, 福建 厦门 361021
2. School of Science, Jimei University, Xiamen 361021, China
高分辨核磁共振(nuclear magnetic resonance,NMR)定域谱是一种重要的分析工具,它能提供精细的分子尺度信息,如化学位移、J耦合等,广泛应用于化学、生物、医学等领域[1-4],但是磁场的不均匀性会导致谱线增宽、信号重叠,而混叠的NMR谱图会影响数据分析.因此如何在不均匀磁场下获取高分辨谱是一个非常重要的研究课题.已有多种技术被应用于在不均匀磁场下获得高分辨NMR谱.一种是匀场技术[5],它可以有效消除大部分磁场的不均匀性,但是这类方法无法完全清除样品内在的磁场不均匀性.另外一种广泛使用的方法是自旋回波技术,该技术利用重聚静磁场不均匀性引起的相位累积从而较好的消除磁场不均匀性,但是该方法只能获得J耦合信息[6].同样地,分子内零量子相干(intramolecular zero-quantum coherence,ZQC)信号能抵抗磁场的不均匀性,但基于ZQC信号获得的高分辨谱也只能提供J耦合信息[7, 8].
正如不均匀磁场导致谱图混叠影响NMR技术的应用一样,过长的采样时间也会严重限制NMR技术的应用.如何快速获取一张高质量的NMR谱图也是一个非常重要的研究领域.可借助谱图处理方法来提高谱图质量,如投影重建方法[9]、线性预测[10]等,进而减少对间接维累加次数的需求,从而显著缩短2D NMR谱的采集时间.压缩感知技术是目前主流的对非均匀采样数据进行谱图重建的技术,该技术通过压缩采样、稀疏表示、算法重建等在欠采样情况下重建出高分辨NMR谱图[11].Frydman小组提出的超快速空间编码方法利用绝热脉冲和线性编码梯度使得样品的空间位置同自旋激发的时间关联起来,可以极大地减少间接维的采样时间,甚至可以在单次扫描的情况下获取二维NMR谱[12-14].
Warren等[15]提出了分子间多量子相干(intermolecular multiple-quantum coherences,iMQCs)概念,该理论认为液体NMR中偶极相互作用分为短程偶极相互作用和长程偶极相互作用.由于分子的快速扩散运动,核自旋之间的短程偶极相互作用平均为0;而长程偶极相互作用则会因为样品不是球形或者磁化矢量受到调制而发生作用[16].由于分子间远程偶极相互作用范围在10~100 μm,远远小于标准的样品尺寸,在偶极相关距离内磁场的不均匀性非常小,因此对于分子间多量子而言,仅在偶极相关距离内(而非整个样品)的磁场不均匀性对谱线线宽的影响非常小,所以可以利用iMQCs信号在不均匀场下获得高分辨NMR谱[17].陈忠课题组[18-21]设计出了一系列基于iMQCs的脉冲序列用于获取高分辨NMR谱,但这些序列都是通过二维采样获取高分辨的一维谱.当磁场不均匀性较大的时候,间接维演化需要数十次乃至数百次的逐步增加演化期t1,从而导致实验时间较长;同时,间接维长的演化时间会显著减少信号强度,尤其是对于横向弛豫时间(T2)短的样品.
哈德曼(Hadamard)波谱与傅里叶变换核磁共振(FT-NMR)技术完全不同,它采用多色软脉冲技术,不仅可以同时激发所选择的多个频点,而且还可以根据需要改变被激发频率点的相位,同时保留相位信息的连续性.Hadamard编解码方法在间接维用固定的时延τ代替了累加次数多的t1维演化,节省了实验时间,也减少了短T2的样品因间接维演化时间长导致的信号严重损失.目前Hadamard波谱技术已经获得了一定的应用,如水峰抑制、数据降维、加快实验速度、选择感兴趣的自旋核等[22-26].
本文提出了一种新的分子间单量子相干(intermolecular single-quantum coherence,iSQC)结合Hadamard编码技术的定域谱方法,用于在不均匀磁场下快速获取高分辨一维NMR定域谱.该脉冲序列被命名为HL-IDEAL-Ⅲ(Hadamard-encoding localized IDEAL-Ⅲ),用N阶Hadamard矩阵编码的多色组合软脉冲选择性激发溶剂峰,间接维t1被固定常量τ代替.而我们之所以选择iSQC信号,是因为iSQC信号有类似于常规单量子信号(single-quantum coherence,SQC)的扩散和弛豫性质[27, 28].
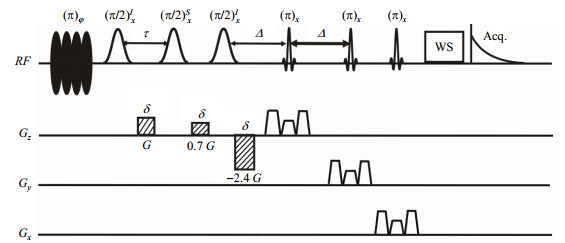
1 理论描述HL-IDEAL-Ⅲ序列如图 1所示.这个脉冲序列是在IDEAL-Ⅲ序列[28]基础上增加了定域模块和一个多色组合软脉冲,该多色组合软脉冲用于选择性激励溶剂峰.与PRESS脉冲序列的定域模块不同,HL-IDEAL-Ⅲ序列采用了三个180°的Sinc软脉冲进行三维定域;同时与PRESS脉冲一样,HL-IDEAL-Ⅲ序列也通过施加对称的破坏梯度的方法来消除杂信号.由于定域模块的存在,HL-IDEAL-Ⅲ序列取消了检测期之前用以形成自旋回波的非选择性的π脉冲.第一个射频(radio frequency,RF)脉冲是多色组合软脉冲,高斯形状软脉冲是选择性脉冲,内有斜线的矩形表示相干选择梯度.“WS”模块表示双“W5”模块的水峰压制模块[29].为了获得0→0→+1→+2→+1→-1的相干选择路径,三个线性的相干选择梯度是1:0.7:-2.4.这种设计方式可以准确选择iSQC信号,并消除SQC信号和其他的iMQC信号.
|
图 1 HL-IDEAL-Ⅲ脉冲序列 Fig. 1 Schematic diagram of HL-IDEAL-Ⅲ sequence |
已有文献[30]在Hadamard-IDEAL-Ⅲ序列的研究中对获得的iSQC信号进行了详细讨论,本文只将其中重要的公式及结论进行介绍,推导过程中辐射阻尼效应、弛豫效应、扩散效应和定域模块都不予考虑.引入线性符号算符
为方便讨论,我们假设采用4阶Hadamard矩阵.Hadamard矩阵如表 1所示.溶剂峰被等分成4块,这4块的中心频点分别为
| 表 1 4阶Hadamard矩阵 Table 1 4-order Hadamard matrix |
| $M({t_2}, z){\rm{ = }} - \frac{{M_0^{{S_k}}}}{2}{J_1}({p_i}{\xi _{{S_k}}})\sum\limits_{j = 1}^4 {\left\{ \begin{gathered} {{\rm{e}}^{{\rm{i}}\left\{ {{\rm{ \mathsf{ π} }}{J_{lk}}{t_2} + [{\omega _{Ij}}\tau + \gamma {\mathit \Delta} B{{(z)}_j}\tau ] - [{\omega _{{S_k}}}{t_2} + \gamma {\mathit \Delta} B{{(z)}_j}{t_2}]} \right\}}} \\ + {{\rm{e}}^{{\rm{i}}\left\{ {[{\omega _{Ij}}\tau + \gamma {\mathit \Delta} B{{(z)}_j}\tau ] - {\rm{ \mathsf{ π} }}{J_{lk}}{t_2} - [{\omega _{{S_k}}}{t_2} + \gamma {\mathit \Delta} B{{(z)}_j}{t_2}]} \right\}}} \\ \end{gathered} \right\}} $ | (1) |
其中,在相关选择梯度作用下,溶剂峰信号会散相.
由于采用4阶的Hadamard矩阵,将得到4个谱信号,将这4个谱信号按照Hadamard矩阵的列进行解码,即可恢复出原信号.例如:Scan1–Scan2+Scan3–Scan4将得到4倍的
| $\begin{gathered} M_{{S_k}}^{{p_1}}({t_2}, z) = - 4\frac{{M_0^{{S_k}}}}{2}{J_1}({\xi _{{S_k}}})\left\{ \begin{gathered} {{\rm{e}}^{{\rm{i}}\left\{ {{\rm{ \mathsf{ π} }}{J_{lk}}{t_2} + [{\omega _{I{p_1}}}\tau + \gamma \Delta B{{(z)}_{_1}}\tau ] - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_1}}{t_2}]} \right\}}} \\ + {{\rm{e}}^{{\rm{i}}\left\{ {[{\omega _{I{p_1}}}\tau + \gamma \Delta B{{(z)}_{_1}}\tau ] - {\rm{ \mathsf{ π} }}{J_{lk}}{t_2} - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_1}}{t_2}]} \right\}}} \\ \end{gathered} \right\} \\ M_{{S_k}}^{{p_2}}({t_2}, z) = - 4\frac{{M_0^{{S_k}}}}{2}{J_1}({\xi _{{S_k}}})\left\{ \begin{gathered} {{\rm{e}}^{{\rm{i}}\left\{ {{\rm{ \mathsf{ π} }}{J_{lk}}{t_2} + [{\omega _{I{p_2}}}\tau + \gamma \Delta B{{(z)}_{_2}}\tau ] - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_2}}{t_2}]} \right\}}} \\ + {{\rm{e}}^{{\rm{i}}\left\{ {[{\omega _{I{p_2}}}\tau + \gamma \Delta B{{(z)}_{_2}}\tau ] - {\rm{ \mathsf{ π} }}{J_{lk}}{t_2} - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_2}}{t_2}]} \right\}}} \\ \end{gathered} \right\} \\ M_{{S_k}}^{{p_3}}({t_2}, z) = - 4\frac{{M_0^{{S_k}}}}{2}{J_1}({\xi _{{S_k}}})\left\{ \begin{gathered} {{\rm{e}}^{{\rm{i}}\left\{ {{\rm{ \mathsf{ π} }}{J_{lk}}{t_2} + [{\omega _{I{p_3}}}\tau + \gamma \Delta B{{(z)}_{_3}}\tau ] - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_3}}{t_2}]} \right\}}} \\ + {{\rm{e}}^{{\rm{i}}\left\{ {[{\omega _{I{p_3}}}\tau + \gamma \Delta B{{(z)}_{_3}}\tau ] - {\rm{ \mathsf{ π} }}{J_{lk}}{t_2} - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_3}}{t_2}]} \right\}}} \\ \end{gathered} \right\} \\ M_{{S_k}}^{{p_4}}({t_2}, z) = - 4\frac{{M_0^{{S_k}}}}{2}{J_1}({\xi _{{S_k}}})\left\{ \begin{gathered} {{\rm{e}}^{{\rm{i}}\left\{ {{\rm{ \mathsf{ π} }}{J_{lk}}{t_2} + [{\omega _{I{p_4}}}\tau + \gamma \Delta B{{(z)}_{_4}}\tau ] - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_4}}{t_2}]} \right\}}} \\ + {{\rm{e}}^{{\rm{i}}\left\{ {[{\omega _{I{p_4}}}\tau + \gamma \Delta B{{(z)}_{_4}}\tau ] - {\rm{ \mathsf{ π} }}{J_{lk}}{t_2} - [{\omega _{{S_k}}}{t_2} + \gamma \Delta B{{(z)}_{_4}}{t_2}]} \right\}}} \\ \end{gathered} \right\} \\ \end{gathered} $ | (2) |
由(2)式可知:首先,这4条谱信号因多色软脉冲激发频点的不同而产生相应位移;其次,激发的频率带宽是实际谱图线宽的理论上限,因此可以通过减少激发的频带来提高谱图的分辨率.可是,当溶剂峰的谱宽一定时,减少激发频带就必须采用高阶的Hadamard矩阵,这也会带来两个问题:其一是实验时间会加长;其二是,多色组合软脉冲激发的频带越窄,持续时间就越久,会严重损失短弛豫时间样品的信号.
2 实验部分 2.1 试剂与样品准备样品一为套管,用于验证HL-IDEAL-Ⅲ序列的定域性.内管是直径为1.7 mm、装有浓度为1 mol/L苏氨酸溶液的玻璃管,外管是直径为5mm、装有浓度为1 mol/L γ-氨基丁酸(GABA)溶液的玻璃管.
样品二为脑模型溶液,由15种不同的脑代谢物的水溶液组成,用于验证HL-IDEAL-Ⅲ序列在复杂体系样品中的性能.这些代谢物分别为肌酸(creatine hydrate,tCr)、N-乙酰-DL-天冬氨酸(N-acetyl-DL-aspartic acid,NAA)、氯化胆碱(choline chloride,tCHo)、L-谷氨酰胺(L-glutamine,Gln)、L-谷氨酸(L-glutamic acid,Glu)、谷胱甘肽(glutathione,GSH)、GABA、肌醇(myo-inositol,m-Ins)、牛磺酸(taurine,Tau)、丙氨酸(alanine,Ala)、乳酸(lactate,Lac),醋酸盐(Acetate,Ace)、N-乙酰天冬氨酰谷氨酸盐(N-Acetylaspartylglutamate,NAAG)、鲨肌醇(scyllo-inositol,s-Ins)和天门冬氨酸(Aspartate,Asp)浓度分别是10.0、12.5、6.0、12.0、12.5、10.0、9.0、15.0、10.0、12.0、10.0、6.0、10.0、10.0和10.0 mmol/L.
实验所用试剂均采购自青岛腾龙微波科技有限公司.
2.2 NMR实验1H NMR实验均在配备有效长度为1.6 cm且有3D梯度线圈的间接检测探头的Varian NMR System 500 MHz NMR谱仪上进行,实验温度为298 K.实验采集到的原始数据需通过Matlab程序后处理.
样品一通过选择不同的体素分次实验来验证HL-IDEAL-Ⅲ序列在不均匀磁场下的定域效果:体素I为4×4×9 mm3,只选择外管;体素II为1×1×8 mm3,只选择内管;体素Ⅲ为4×4×16 mm3,选择内外管.样品一采集了以下几种NMR谱图,包括不均匀磁场下(通过改变x1、y1和z1方向的匀场线圈电流产生150 Hz线宽的不均匀磁场)使用HL-IDEAL-Ⅲ序列获得的体素Ⅰ、Ⅱ和Ⅲ的高分辨1H NMR谱图,以及使用PRESS序列获得的体素Ⅲ的1H NMR谱图.90°硬脉冲的时间是10.8 μs,谱宽为5 000 Hz.演化期的固定时延τ=5 ms.选择溶质的π/2软脉冲由硬脉冲和与该π/2硬脉冲相位相反的选择溶剂的π/2软脉冲代替.π/2高斯软脉冲的作用时间=6 ms,相干选择梯度的强度G=0.1 T/m,持续时间δ=1.2 ms,脉冲重复时间=3.5 s,回波时间Δ=34 ms,采样时间t2=0.1 s,总采样时间=4.3 min.
样品二采集了4种谱图:均匀磁场下使用PRESS序列的1H NMR谱;以及不均匀磁场下(通过改变x1、y1和z1方向的匀场线圈电流产生150 Hz线宽的不均匀磁场)的单脉冲一维1H NMR谱、使用PRESS脉冲序列采集的1H NMR谱和使用HL-IDEAL-Ⅲ脉冲序列采集的高分辨1H NMR谱.90°硬脉冲的时间是9.9 μs,谱宽为5 000 Hz.体素是4×4×16 mm3.其他参数分别是:τ=5.7 ms,Δ=42 ms,间接维累进次数nt=16.选择激发溶剂峰的π/2软脉冲作用时间=10.1 ms.相干选择梯度的强度G=0.1 T/m,持续时间δ=1.2 ms,采样时间t2=0.1 s,总采样时间=16.5 min.在预饱和实验中nt=32.在使用PRESS脉冲序列的实验中,重复时间(TR)是4.0 s,重复次数是32,采用序列自带的压水峰模块(VAPOR).在使用HL-IDEAL-Ⅲ脉冲序列的实验中,Hadamard矩阵选择16阶矩阵,通过该矩阵生成的多色组合软脉冲的持续时间是200 ms,激发带宽为20 Hz.在多色组合软脉冲中,激发带宽越小,脉冲的持续时间越长;反之,则越短.根据(2)式所知,当使用高阶的Hadamard矩阵减少激发带宽时,可以提高谱图分辨率,但是这会导致多色组合软脉冲的作用时间变长,从而加剧信号衰减,降低谱图的信噪比,进而导致扫描次数增加,实验时间变长.因此使用HL-IDEAL-Ⅲ序列因为激发频带不能太小,导致获得的谱图分辨率有一定的局限性.如果使用16阶的Hadamard矩阵,采用20 Hz的激发频带,使用HL-IDEAL-Ⅲ序列只能区分间隔在均匀磁场下大于20 Hz的谱峰.而且为了避免软脉冲激发到附近的溶质峰,HL-IDEAL-Ⅲ序列检测的样品必须满足以下条件:本文的溶剂峰与最近的溶质峰在不均匀磁场下展宽后不能够严重混叠.为了能较好地消除干扰信号,实验中采用了4步相位循环:第2个脉冲、第4个脉冲和接收机的相位分别为
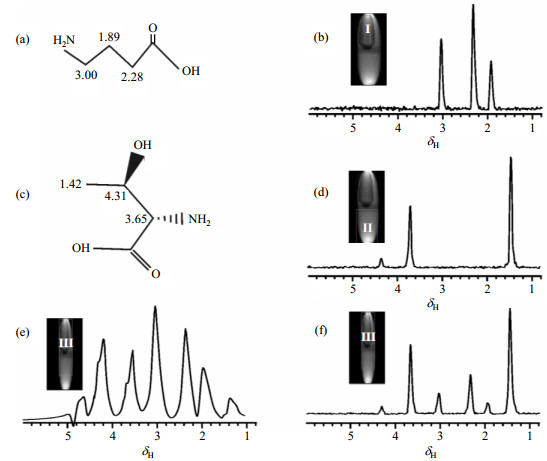
不均匀磁场下GABA[结构如图 2(a)所示]溶液和苏氨酸[结构如图 2(c)所示]溶液套管实验结果如图 2所示.图 2(b)、2(d)和2(f)分别为体素Ⅰ、Ⅱ和Ⅲ在不均匀磁场中使用HL-IDEAL-Ⅲ序列获得的1H NMR谱,图 2(b)中只有GABA的信号,图 2(d)中只有苏氨酸的信号,这充分说明HL-IDEAL-Ⅲ序列在不均匀磁场下具有很好的定域能力.图 2(b)、2(d)和2(f)中均不存在溶剂峰信号,这一结果与理论推导的溶剂峰散相一致.图 2(e)为体素Ⅲ在不均匀磁场中使用PRESS序列获得的1H NMR谱,通过比较图 2(e)和2(f),可以发现使用HL-IDEAL-Ⅲ序列获得的NMR谱图的分辨率明显更高.为了观察不均匀磁场下样品边界处的峰信号是否会相互干扰,实验选择体素时应尽量选择大体素.由于PRESS序列是点体素定位,而且是基于信号比较强的SQC信号,所以当采取小体素实验时,使用PRESS序列能获得分辨率较高的谱图;可是当选择大体素时,PRESS序列无法抵抗不均匀磁场的影响.但是使用HL-IDEAL-Ⅲ序列即使在选择大体素、且该体素靠近边界时,依然能获得分辨率较高的谱图.这一实验结果充分说明使用HL-IDEAL-Ⅲ序列在不均匀磁场下可以准确定域,并能获取高分辨谱图.
|
图 2 不均匀磁场下,套管实验验证HL-IDEAL-Ⅲ序列的定域性.(a) GABA的分子结构;(b)使用HL-IDEAL-Ⅲ序列获得的体素I(外管,装有1 mol/L GABA溶液)的高分辨1H NMR谱图;(c)苏氨酸的分子结构;(d)使用HL-IDEAL-Ⅲ序列获得的体素II(内管,装有1 mol/L苏氨酸溶液)的高分辨1H NMR谱图;(e)使用PRESS序列获得的体素Ⅲ(内外管)的1H NMR谱图;(f)使用HL-IDEAL-Ⅲ序列获得的体素Ⅲ(内外管)的高分辨1H NMR谱图 Fig. 2 Localization performance evaluation for HL-IDEAL-Ⅲ pulse sequence under an inhomogeneous field. (a) Molecular structure of GABA; (b) 1H NMR spectrum of voxel I (outer tube with 1 mol/L GABA solution) acquired using HL-IDEAL-Ⅲ pulse sequence; (c) Molecular structure of threonine; (d) 1H NMR spectrum of voxel II (inner tube with 1 mol/L threonine solution) acquired using HL-IDEAL-Ⅲ pulse sequence; (e) 1H NMR spectrum of voxel Ⅲ (outer and inner tubes) acquired using PRESS pulse sequence; (f) 1H NMR spectrum of voxel Ⅲ (outer and inner tubes) acquired using HL-IDEAL-Ⅲ pulse sequence |
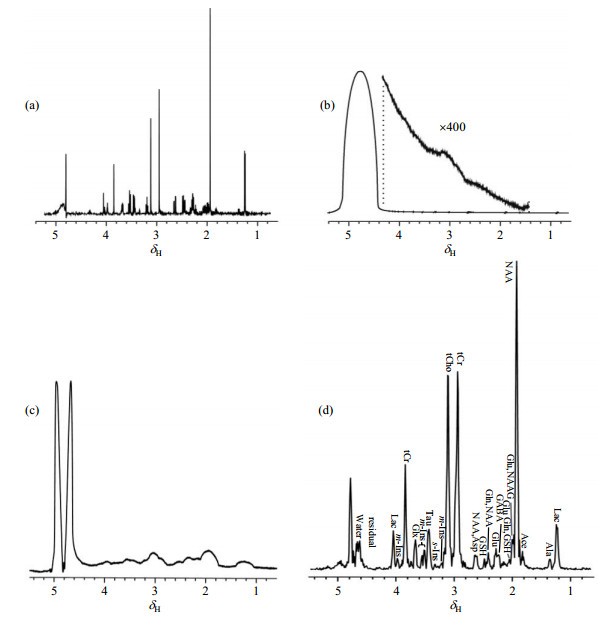
脑模型的实验结果如图 3所示.图 3(a)为均匀场下,使用PRESS序列获得的1H NMR谱,最高峰的线宽为3.1 Hz.图 3(b)和3(c)为不均匀场下,单脉冲一维1H NMR谱图和使用PRESS序列获得的1H NMR谱图,几乎不能提供任何有效信息.在相同的不均匀磁场下,使用HL-IDEAL-Ⅲ序列得到的NAA线宽为20.2 Hz的高分辨1H NMR谱图如图 3(d)所示,显著优于图 3(b)和3(c).脑模型实验充分说明使用HL-IDEAL-Ⅲ序列即使在不均匀场下,也可以在很短时间内获得非常有用的信号.
|
图 3 (a) 均匀场下使用PRESS序列,以及不均匀场下使用(b)传统一维序列、(c) PRESS序列和(d) HL-IDEAL-Ⅲ序列获得的脑模型的1H NMR谱图. Lac(乳酸),Ala(丙氨酸),Ace(醋酸盐),NAA(N-乙酰-DL-天冬氨酸),Glu(L-谷氨酸),NAAG(N-乙酰天冬氨酰谷氨酸盐),Gln(L-谷氨酰胺),GSH(谷胱甘肽),GABA(γ-氨基丁酸),Asp(天门冬氨酸),tCr(肌酸),tCho(氯化胆碱),m-Ins(肌醇),s-Ins(鲨肌醇),Tau(牛磺酸),Glx(L-谷氨酸和L-谷氨酰胺) Fig. 3 1H NMR spectra of brain metabolites using (a) PRESS sequence under well-shimmed field, and (b) conventional 1D sequence, (c) PRESS sequence, and (d) HL-IDEAL-Ⅲ sequence under the inhomogeneous field. Lac (Lactate), Ala (Alanine), Ace (Acetate), NAA (N-acetyl-DL-aspartic acid), Glu (L-Glutamic acid), NAAG (N-Acetylaspartylglutamate), Gln (L-Glutamine), GSH (Glutathione), GABA (γ-Aminobutyrate), Asp (Aspartate), tCr (Creatine hydrate), tCho (Choline chloride), m-Ins (myo-inositol), s-Ins (scyllo-inositol), Tau (Taurine), Glx (Gln and Glu) |
需要指出的是,尽管使用HL-IDEAL-Ⅲ序列获得的1H NMR谱图分辨率较高,但受限于多色组合软脉冲的激发带宽,分辨率无法优于均匀磁场下使用PRESS序列获得的1H NMR谱图;而且由于iSQC信号比SQC信号弱,有少量的谱峰信息被破坏,谱图的信噪比也低于均匀场下常规PRESS波谱.虽然从理论上分析,采用HL-IDEAL-Ⅲ序列当使用16阶Hadamard矩阵解码后应该得到15条相同的、只是存在化学位移平移的高分辨1D 1H NMR谱图,通过解码后谱图的累加可以提高信噪比.但在实际实验中,只有部分高分辨1D 1H NMR谱图满足要求,这可能是由多色组合软脉冲的不精确性、磁场的不稳定性以及采样期噪声的随机性等原因导致的.与传统NMR谱图间接维数据可以完全累加相比,使用HL-IDEAL-Ⅲ序列会舍弃部分解码后的数据,从而降低了谱图信噪比.解决这一问题的途径包括增加累加次数(这会显著增加实验时间),使用低温探头或者更高场强的谱仪等.
4 结论本文首先对使用HL-IDEAL-Ⅲ序列获得的信号进行了理论推导和分析.然后利用套管实验和脑模型实验验证了不均匀磁场下,HL-IDEAL-Ⅲ序列具有良好的定域能力和可行性,并且可以很好的压制溶剂峰,实验结果与理论分析相符.上述结果证实在不均匀磁场下,使用HL-IDEAL-Ⅲ序列可以快速获取高分辨1D 1H NMR定域谱.但同时也存在谱图信噪比较低的问题,如何进一步提高使用HL-IDEAL-Ⅲ序列获得谱图的信噪比需要进一步研究.
| [1] | HUANG Y Q, CAI S H, ZHANG Z Y, et al. High-resolution two-dimensional J-resolved NMR spectroscopy for biological systems[J]. Biophys J, 2014, 106(9): 2061-2070. DOI: 10.1016/j.bpj.2014.03.022. |
| [2] | CUI X H, BAO J F, HUANG Y Q, et al. In vivo spatially localized high resolution 1H MRS via intermolecular single-quantum coherence of rat brain at 7 T[J]. J Magn Reson Imaging, 2013, 37(2): 359-364. DOI: 10.1002/jmri.23839. |
| [3] | CHEN H, ZHANG Z Y, WANG K Y, et al. Ultrafast 1H J-resolved spectroscopy via 2H distant dipolar field in magnetic fields with unknown spatial variations[J]. Chem Phys Lett, 2013, 587: 99-104. DOI: 10.1016/j.cplett.2013.09.045. |
| [4] | ROUSSEL T, GIRAUDEAU P, RATINEY H, et al. 3D localized 2D ultrafast J-resolved magnetic resonance spectroscopy:in vitro study on a 7 T imaging system[J]. J Magn Reson, 2012, 215: 50-55. DOI: 10.1016/j.jmr.2011.12.013. |
| [5] | KOCH K M, SACOLICK L I, NIXON T W, et al. Dynamically shimmed multivoxel 1H magnetic resonance spectroscopy and multislice magnetic resonance spectroscopic imaging of the human brain[J]. Magn Reson Med, 2007, 57(3): 587-591. DOI: 10.1002/mrm.21141. |
| [6] | HURLIMANN M D. Encoding of diffusion and T1 in the CPMG echo shape:single-shot D and T1 measurements in grossly inhomogeneous fields[J]. J Magn Reson, 2007, 184(1): 114-129. DOI: 10.1016/j.jmr.2006.09.021. |
| [7] | DE GRAAF R A, KLOMP D W J, LUIJTEN P R, et al. Intramolecular zero-quantum-coherence 2D NMR spectroscopy of lipids in the human breast at 7 T[J]. Magn Reson Med, 2014, 71(2): 451-457. DOI: 10.1002/mrm.24701. |
| [8] | DE GRAAF R A, ROTHMAN D L, BEHAR K L. High resolution NMR spectroscopy of rat brain in vivo through indirect zero-quantum-coherence detection[J]. J Magn Reson, 2007, 187(2): 320-326. DOI: 10.1016/j.jmr.2007.06.001. |
| [9] | JIANG B, JIANG X W, XIAO N, et al. Gridding and fast Fourier transformation on non-uniformly sparse sampled multidimensional NMR data[J]. J Magn Reson, 2010, 204(1): 165-168. DOI: 10.1016/j.jmr.2010.02.009. |
| [10] | STERN A S, LI K B, HOCH J C. Modern spectrum analysis in multidimensional NMR spectroscopy:comparison of linear-prediction extrapolation and maximum-entropy reconstruction[J]. J Am Chem Soc, 2002, 124(9): 1982-1993. DOI: 10.1021/ja011669o. |
| [11] | LIU Y S, ZHAN Z F, CAI J F, et al. Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging[J]. IEEE T Med Imaging, 2016, 35(9): 2130-2140. DOI: 10.1109/TMI.2016.2550080. |
| [12] | FRYDMAN L, LUPULESCU A, SCHERF T. Principles and features of single-scan two-dimensional NMR spectroscopy[J]. J Am Chem Soc, 2003, 125(30): 9204-9217. DOI: 10.1021/ja030055b. |
| [13] | FRYDMAN L, BLAZINA D. Ultrafast two-dimensional nuclear magnetic resonance spectroscopy of hyperpolarized solutions[J]. Nat Phys, 2007, 3(6): 415-419. DOI: 10.1038/nphys597. |
| [14] | SHROT Y, FRYDMAN L. Spatial encoding strategies for ultrafast multidimensional nuclear magnetic resonance[J]. J Chem Phys, 2008, 128(5): 052209. DOI: 10.1063/1.2834733. |
| [15] | AHN S, WARREN W S, LEE S. Quantum treatment of intermolecular multiple-quantum coherences with intramolecular J coupling in solution NMR[J]. J Magn Reson, 1997, 128(2): 114-129. DOI: 10.1006/jmre.1997.1226. |
| [16] | BERGER S. NMR techniques employing selective radiofrequency pulses in combination with pulsed field gradients[J]. Prog Nucl Magn Reson Spectro, 1997, 30(3/4): 137-156. |
| [17] | LIN Y Y, AHN S, MURALI N, et al. High-resolution, > 1 GHz NMR in unstable magnetic fields[J]. Phys Rev Lett, 2000, 85(17): 3732-3735. DOI: 10.1103/PhysRevLett.85.3732. |
| [18] | LIN M J, CHEN X, CAI S H, et al. High-resolution magnetic resonance spectroscopy in unstable fields via intermolecular zero-quantum coherences[J]. Phys Chem Chem Phys, 2010, 12(23): 6014-6020. DOI: 10.1039/b920180g. |
| [19] | CHEN Z, CHEN Z W, ZHONG J H. High-resolution NMR spectra in inhomogeneous fields via IDEAL (intermolecular dipolar-interaction enhanced all lines) method[J]. J Am Chem Soc, 2004, 126(2): 446-447. DOI: 10.1021/ja036491f. |
| [20] | HUANG Y Q, CAI S H, CHEN X, et al. Intermolecular single-quantum coherence sequences for high-resolution NMR spectra in inhomogeneous fields[J]. J Magn Reson, 2010, 203(1): 100-107. DOI: 10.1016/j.jmr.2009.12.007. |
| [21] | CHEN X, LIN M J, CHEN Z, et al. High-resolution intermolecular zero-quantum coherence spectroscopy under inhomogeneous fields with effective solvent suppression[J]. Phys Chem Chem Phys, 2007, 9(47): 6231-6240. DOI: 10.1039/b709154k. |
| [22] | KUPCE E, FREEMAN R. Frequency-domain Hadamard spectroscopy[J]. J Magn Reson, 2003, 162(1): 158-165. DOI: 10.1016/S1090-7807(02)00194-5. |
| [23] | KUPCE E, NISHIDA T, FREEMAN R. Hadamard NMR spectroscopy[J]. Prog Nucl Magn Reson Spectro, 2003, 42(3/4): 95-122. |
| [24] | FLEYSHER L, FLEYSHER R, LIU S T, et al. Voxel-shift and interpolation for Hadamard-encoded MR images[J]. Magn Reson Med, 2008, 60(3): 524-535. DOI: 10.1002/mrm.21687. |
| [25] | CAI C B, GAO F L, CAI S H, et al. Fast high-resolution 2D correlation spectroscopy in inhomogeneous fields via Hadamard intermolecular multiple quantum coherences technique[J]. J Magn Reson, 2011, 211(2): 162-169. DOI: 10.1016/j.jmr.2011.05.008. |
| [26] | ZHANG Z Y, CAI S H, WANG K Y, et al. Fast high-resolution 2D NMR spectroscopy in inhomogeneous fields via Hadamard frequency encoding and spatial encoding[J]. Chem Phys Lett, 2013, 582: 148-153. DOI: 10.1016/j.cplett.2013.07.036. |
| [27] | CHEN Z, CHEN Z W, ZHONG J H. Observation and characterization of intermolecular homonuclear single-quantum coherences in liquid nuclear magnetic resonance[J]. J Chem Phys, 2002, 117(18): 8426-8435. DOI: 10.1063/1.1512649. |
| [28] | HUANG Y Q, CAI S H, CHEN X, et al. Intermolecular single-quantum coherence sequences for high-resolution NMR spectra in inhomogeneous fields[J]. J Magn Reson, 2010, 203(1): 100-107. DOI: 10.1016/j.jmr.2009.12.007. |
| [29] | PRICE W S. Water signal suppression in NMR spectroscopy[J]. Annu Rep Nmr Spectro, 1999, 38: 289-354. DOI: 10.1016/S0066-4103(08)60040-X. |
| [30] | KE H P, CAI H H, CAI S G, et al. Hadamard-encoded high-resolution NMR spectroscopy via intermolecular single-quantum coherences[J]. J Chem Phys, 2014, 444: 61-65. |
 2020, Vol. 37
2020, Vol. 37 
