2. State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, National Center for Magnetic Resonance in Wuhan(Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences), Wuhan 430071, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
2. 波谱与原子分子物理国家重点实验室, 武汉磁共振中心(中国科学院 武汉物理与数学研究所), 湖北 武汉 430071;
3. 中国科学院大学, 北京 100049
Quantitative analysis lies in the core of nuclear magnetic resonance (NMR) spectroscopy. The quantitative NMR measurements can provide accurate information of, either relative or absolute, content of components or species in the sample. It's required in a reliable quantitative NMR experiment that the signal intensity of each magnetically in-equivalent site is proportional to the number of corresponding spins. The simplest and commonly used method in quantitative NMR for 1/2-spin nuclei is the single pulse (SP) experiment, where the spin magnetization is directly excited via a 90° pulse followed by acquisition. To make sure all the spin magnetizations undergo near complete recovery characterized by the longitudinal relaxation with time constant of T1, the SP experiment must require sufficient recycle delay (> 5 T1). However, for dilute spin with excessively long T1, the SP experiment would be very inefficient, and extremely time-consuming. Even with the small angle excitation[1], the poor acquisition efficiency is hardly to be overcome.
Cross polarization (CP) is one of the most important techniques in solid-state NMR spectroscopy, and it has been commonly used for obtaining spectra of dilute spins under both static and magic-angle spinning (MAS) conditions[2]. By virtue of the polarization transfer from abundant spins, especially proton, to the coupled dilute spins, the recorded CP NMR spectra have higher signal intensity than that by direct excitation. Besides, because the CP starts from the excitation of abundant spins, the recycle delay depends on the longitudinal relaxation of abundant spins that is usually much shorter than that of dilute spins. As a result, CP has much higher acquisition efficiency than the SP experiment.
In CP NMR experiment, simultaneous spin-locks are applied on both abundant spin (I) and dilute spin (S) channels. The strength of the two radio frequency (RF) irradiations,
| $ {\omega _I} - {\omega _S} = \pm n{\omega _r} $ | (1) |
where
The following review introduces the quantitative CP methods chronologically, according to the main characteristics of each one of them. Specifically, the CP with variable amplitude broadens the HH matching condition under MAS conditions; the multiple-contact CP accomplishes successive accumulation of S signal under the repetitively restored I polarization; quantification of CP (QCP) compensates the effect of T1ρ relaxation in the cross polarization/cross depolarization (CP/CDP) reciprocity relation; Lee-Goldburg frequency modulated CP (LG-FMCP) prolongs the T1ρ relaxation times during the spin lock period; quantitative CP (QUCP), being independent to T1, can reach uniform enhancement no matter what the recycle delay is.
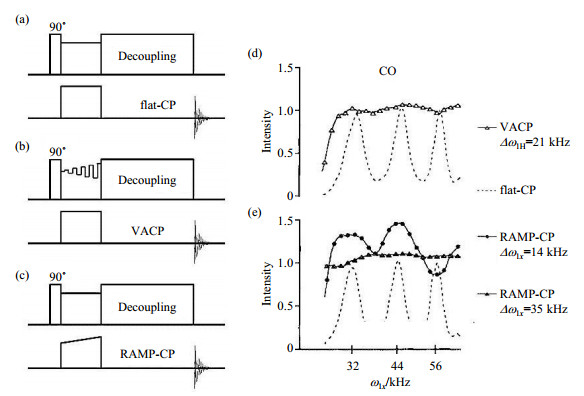
1 Variable amplitude CPAs mentioned above, the flat-CP [Fig. 1(a)] often results in non-uniform enhancement factor for each magnetically non-equivalent site, in addition, the overall enhancement efficiency is very sensitive to RF mismatches and the offset of resonance frequency, especially under MAS condition. In the early 1990s, in order to improve the robustness of flat-CP, the variable-amplitude CP [VACP, Fig. 1(b)] was proposed by Peersen et al.[21] The VACP is basically a train of flat-CPs with different amplitude and constant phase in one channel, while a spin-lock irradiation with constant amplitude and phase is applied in another channel. It could suppress the influence of resonance offset and broaden the CP HH match conditions. Then the idea of variable amplitude was further extended with the bringing up of ramped-amplitude CP (RAMP-CP)[10, 22, 23]. Instead of the discrete steps with varied amplitudes in VACP, the irradiation in RAMP-CP contains smoother, monotonically varying power [Fig. 1(c)], which makes the HH matching profile much broader than the flat-CP NMR experiment [Fig. 1(d) and 1(e)].
|
Fig. 1 The pulse sequences of (a) flat-CP, (b) VACP and (c) RAMP-CP, as well as (d, e) their HH matching profiles of 13C=O group in a mixture of three labelled amino acids: 1-13C=O glycine, 13CH2-15N glycine, t-boc-3-13CH3-alanine. The VACP showed in (d) used amplitude variation Δω1H of 21 kHz, and theΔω1x of two RAMP-CP experiments were 14 kHz and 35 kHz in (e). The NMR spectrometer in these experiments was Chemagnetics CMX-360 with spinning speed of 12 kHz (Reproduced according to Ref. [22]) |
The RAMP-CP can only obtain quantitative NMR spectra in spin systems where the longitudinal relaxation rate in rotating frame, T1ρ, I, is much longer than the cross relaxation time, TIS, which is determined by I-S dipolar coupling[10]. The signal of S spins builds up quickly while the decay of I spin polarization being slow. It suggests that the quantitative RAMP-CP experiment is more suited for the spin systems with strong I-S dipolar coupling, more specifically, the systems with dilute S spins "immersed" in the abundant I spins. Consequently, there exists a time of spin locking sufficiently long for the signals of S spins to build up to the same factor close to
However, for systems with relatively weak I-S dipolar coupling, TIS will be comparable to, or even larger than T1ρ, I. In this circumstance, significant decay could occur prior to the corresponding S signals reach the maximum enhancement factor of
In the regular flat-CP experiments, the magnetization of I spins is transferred to the closest S spins that match the HH conditions, then transferred among S spins via I-I and S-S spin diffusion[24]. Usually the spin diffusion rate of dilute S spin is slow due to the dilute S-S spin network and relatively weak S-S dipolar couplings. It makes the signal of S spins only partially enhanced after a single flat-CP, and the portion of enhanced S spins strongly depends on CP HH matching condition. As a result, the uniform enhancement is hampered.
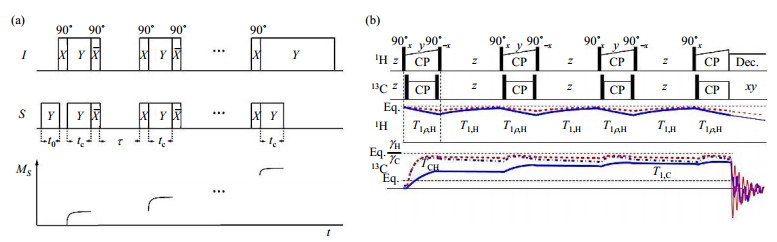
One solution is to perform multiple-contact CP whose concept was first introduced in 1985[25]. In 1990, Zhang et al.[8] applied the multiple-contact CP on the model compounds such as glycine, to investigate the CP dynamics during the multiple CP contacts. The multiple-contact CP consisted of successive CP contacts, and each CP contact was separated by 90° pulses on both I and S channels as shown in Fig. 2(a). After the first CP, the magnetization of I and S (denoted MI and MS) spins were both converted back to z direction by 90° pulse, then the spin system underwent a delay τ. The τ was set shorter than the spin-lattice relaxation time of S spins T1, S, but longer than T1, I, and it's sufficient for S spins to reach a quasiequilibrium state via spin diffusion. During the delay τ, the MI was recovered via T1 relaxation, and the MS was stored on z direction without significant loss. At the end of τ, MI and MS were both converted to transversal magnetization by 90° pulses, and then followed by spin lock, i.e. the second CP. As it turned out, with the increasing number of CP contacts, the multiple-contact CP would render accumulation of MS. As demonstrated in the examples of (NH4)H2PO4 and glycine, the signal of 31P and 13C built up and almost reach their maximum enhancement factors[8]. For the short spin-locking contact time, the mismatched multiple-contact CP could lead to faster signal build up than that with matched HH conditions. It's conclusive that the mismatched multiple-contact CP is more suitable for the samples with fast T1ρ decay, where the repetitive short CP contacts would be able to establish uniform enhancement. However, multiple-contact CP is not robust to RF mismatch, and also, the performance can be hampered by the imperfection of 90° pulse[26].
|
Fig. 2 Pulse sequences for (a) multiple-contact CP (reproduced according to Ref. [8]) and (b) multiCP (Reproduced according to Ref. [18]). The curves plotted below each sequence show the evolution of the spin magnetizations. In Fig. (b), those curves are produced via numerical simulation with various conditions: CHn with dipolar coupling TCH=0.2 ms, relaxation time T1ρ, H=12 ms and T1ρ, C=10 s, plotted in dashed red line; CHn with identical TCH, while T1ρ, H=5 ms and T1ρ, C=3 s, plotted in dash-dotted blue line; non-protonated carbon with TCH=1 ms, T1ρ, H=5 ms and T1ρ, C=10 s, plotted in solid blue line |
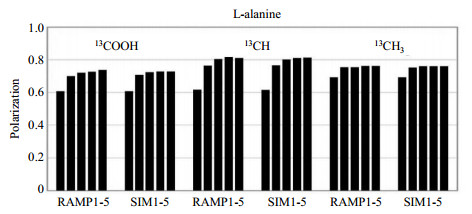
By incorporating with RAMP-CP, the performance of multiple-contact CP can be further improved, and such modified multiple-contact CP technique is called as multiCP[18, 19] [Fig. 2(b)]. As mentioned above, the RAMP-CP with linearly varying amplitude could broaden the HH matching condition, and enlarge the portion of enhanced S spins in a single CP contact. The two-stage process therefore becomes obscure, and a single RAMP-CP contact won't result in quasiequilibrium state. As shown in Fig. 2(b), the signals of S spins keep growing with the increasing number of RAMP-CP contacts. The dynamics during the following delay in multiCP is similar to the multiple-contact CP. For instance, in 1H-13C multiCP experiments for natural abundant L-alanine[19], the 13C signal would reach a plateau after the third contact. Due to the shorter T1ρ and weaker 1H-13C dipolar coupling of COOH group, the corresponding polarization factor of the plateau was noticeably less than those of CH and CH3 groups, and less than the theoretical limit (normalized to 1), albeit with good agreement to the simulation. The multiCP NMR results showed that three carbon signals had a disparity of ±6.5% at the third contact, and after the fifth contact, this signal disparity could be reduced to ±4.7%. However, due to the intrinsic T1ρ distributions in the sample, more contact number resulted in no further improvement (Fig. 3). Theoretically, the efficient compensation on the effect caused by T1ρ distribution could lower the signal disparity to ±0.5%, suggesting other approach to accomplish quantitative CP, which will be discussed in the next section.
|
Fig. 3 The experimental (RAMP1-5) and simulation (SIM1-5) results of 13COOH, 13CH, 13CH3 groups in L-alanine, where the 1-5 denotes the number of RAMP-CP block. It's noted that all three carbon groups have the same polarization factor of 0.251 5 in the quantitative SP NMR experiment with d1 = 80 s. The spinning frequency was 11 kHz, and the HH condition for CP was 66 kHz for ω1H with the ω1C ranging from 53 kHz to 55 kHz in 50 steps. The CP blocks were separated by 1 s delay (Reproduced according to Ref. [18]) |
For systems with strongly coupled I-S spin pairs, the multiCP can provide the quantitative information with higher accuracy. For example, multiCP played a crucial part in the structural characterization of a group of organic polymers known as copolymerized conjugated microporous polymers (CP-CMPs), as reported by Brownbill et al.[27] The CP-CMPs have three-dimensional networks that constructed by pyrene and benzene (Fig. 4), and have high activity as photocatalysts in decomposing water to generate hydrogen. However, the amorphism and insolubility make it challenging to investigate the structure of CP-CMP, obscuring the relation between synthesis and the polymer composition. Brownbill et al. proved that the structure of CP-CMPs was directly related to the feed ratio of monomers, using dynamic nuclear polarization (DNP) enhanced 1H-13C CP NMR experiments. Furthermore, by virtue of DNP enhanced 1H-13C multiCP NMR technique, they investigated the relation between the feed ratio and the composition of final polymers (Table 1). The quantitative NMR spectra was accomplished by integration through all resonances in multiCP 13C NMR spectrum, then dividing the sum area by the number of carbon atom in the corresponding monomer unit. The results revealed that the final polymers had the identical, within error, pyrene/benzene ratio with the feed ratio in monomers, indicating near complete uptake of raw materials during the synthesis. This finding was instructive for alternating the CP-CMP structure therefore modulating the band gap[27]. With the multiCP NMR method, one could also obtain the absolute content of multiple components in system of interest. By means of calibration curve, King et al.[28] determined the purity of chitin in the ground shrimp shells. The results agreed well with that by other established method. More importantly, the quantitative analysis by multiCP was quicker, more accurate, and not harmful to the sample. Therefore it's suitable for fast purity measurement during chitin purification form shrimp shells.

|
Fig. 4 The hypothesized structure of one of the CP-CMPs, CP-CMP10 and the corresponding DNP enhanced (green) and multiCP (light green) 13C MAS NMR spectra. The dashed black line indicates the spectrum from simulation, and dashed gray for spectral deconvolution. The difference spectrum between experimental and simulated one is depicted in solid gray line. The spectra were recorded on a 400 MHz NMR spectrometer[27] |
| Table 1 Monomer feed ratios and DNP 13C multiCP integration of several CP-CMPs[27] |
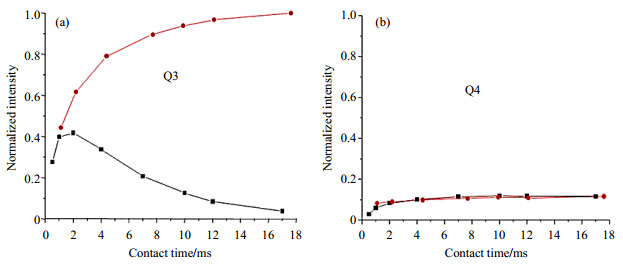
The deviation by multiCP from theoretical limit can be more obvious when it is applied to the samples containing weak I-S dipolar coupling. Sam et al.[29] investigated a class of silicate-siloxane copolymers called POSiSils via 1H-29Si multiCP technique. The T1 of 29Si in these copolymers were in the range of 50~160 s, indicating excessively long recycle delay of 800 s for quantitative NMR experiments by the direct excitation, while the recycle delay in regular RAMP-CP MAS NMR experiment was significantly shortened due to T1, H < 1 s. As shown in the buildup curves of CP dynamics [Fig. 5(a)], the 29Si signal from Q3 site, in which Si atom is connected to one O-H and three O-Si groups, would start decaying due to the short T1ρ when the contact time is longer than 2 ms, and the maximum normalized enhancement factor was only 0.5. By performing the multiCP approach, the enhancement factor of Q3 could be improved close to 1.0, where totally 16 CP contacts were applied with individual CP contact time of 1.1 ms and tz delay of 2.5 s [Fig. 5(a)]. However, an enhancement factor larger than 0.2 couldn't be achieved for the 29Si bonded to four O-Si groups, i.e. Q4 site, neither by regular RAMP-CP nor multiCP technique. As shown in Fig. 5(b), no much difference was observed in the CP dynamics plots of 29Si Q4 site, which is mainly due to very weak 1H-29Si dipolar couplings of Q4 with H in surroundings. These results demonstrated the limitation of multiCP applications in the systems with long TIS (or weak I-S dipolar network). In addition, multiCP technique can be used for sensitivity enhancement in multi-dimensional NMR experiments, for instance, 2D 29Si-29Si DQ-SQ correlation spectroscopy with multiCP excitation but not a regular RAMP-CP[29].
|
Fig. 5 Intensity of 29Si NMR signal from (a) Q3 and (b) Q4 sites in POSiSil-2, enhanced by 1H-29Si single CP (black box) and multiCP (red circle). Each CP contact in multiCP was set to 1.1 ms, and separated by a delay of 2.5 s. The NMR experiments were carried out on Bruker Avance NMR spectrometer with proton frequency of around 500 MHz (Reproduced according to Ref. [29]) |
The HH CP acts as a forward polarization transfer, and in fact there is a reverse process, called as CDP[14, 30], which is conformed to a reciprocity relation:
| $ Sum(t) = CP(t) + CDP(t) = 1 $ | (2) |
together with CP[14, 31, 32]. The reciprocity relation suggests that, in an ideal system without relaxation, the sum of the polarization transferred forwards and backwards should be a constant that can be normalized to 1. Obviously, in the practical systems, the relaxation will make Sum(t) time-dependent and decay (Fig. 6), i.e.,
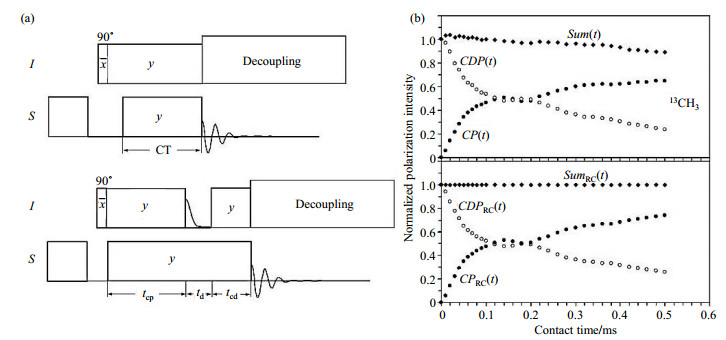
|
Fig. 6 (a) Cross polarization (upper, "forward" transfer) and cross depolarization (lower, "backward" transfer); (b) Experiments of reciprocity relation (upper) and compensated reciprocity relation (lower). For CP in (a), a small delay was placed in the S channel after the first 90° pulse of I channel, in order to avoid possible transient oscillation of I spin polarization. In both sequences, the S spins were saturated prior to the first 90° pulse. The experiments in (b) were carried out on Bruker CSX-300 NMR spectrometer with proton frequency of 300 MHz and the spinning speed was 5 kHz (Reproduced according to Ref. [14]) |
| $ Sum'(t) = CP'(t) + CDP'(t) = f(t) $ | (3) |
As the decay of Sum'(t) is dominated by T1ρ, it can be assumed:
| $ f\left( t \right){\rm{ }} \approx {\rm{ exp }}( - t/{T_{1\rho }}){\rm{ }} \approx {\rm{ }}1 - t/{T_{1\rho }},{\rm{for}}\;\;t < < {T_{1\rho }} $ | (4) |
Once T1ρ is measured by fitting the Sum'(t) curve, the CP'(t) and CDP'(t) can be compensated via dividing by Sum'(t). As reported by Shu et al.[14, 20], the reciprocity relation could be revised by compensating the relaxation effect.
With the relaxation effect compensated, the signal intensity of S spins is relatively independent on T1ρ relaxation, which would allow for achieving quantitative information in the samples (QCP)[14, 20]. For instance, there are equal numbers of 13C in CO, CH and CH3 groups in alanine, thus uniform enhancement in a quantitative CP/MAS spectrum should give the same peak intensity for all three groups. However, by the regular CP, the deviation of 13C CP/MAS signals with a contact time of 0.1 ms is ±60.4% from the uniform enhancement. On the other hand, the deviation by QCP was reduced to ±3.4% even without T1ρ compensation, and could be further reduced ±0.5% with the T1ρ compensation, which indicated that uniform enhancement was achieved. To further demonstrate the performance of the QCP method, a sample of glycine/alanine mixture with molar ratio of 2.765 was prepared. As demonstrated in 13C QCP NMR experiment with a contact time of 0.5 ms, the ratio of 13CH2 (glycine) and 13CH (alanine) signal intensities was 2.770 with an error of ±0.005[12]. Notably, the QCP method is also suitable for the isotope labeled systems. In a mixture of 13C-labelled alanine and natural abundant glycine, the molar ratio of the two components determined by the QCP method was 10.62, in good agreement with 10.82 by single pulse NMR experiment[20].
In comparison, the QCP method could improve the uniformity of enhancement, and significantly decrease the experimental error in quantitative NMR measurement. However, T1ρ measurement would be required to obtain sufficient accuracy, where it's recommended that at least four NMR experiments are needed[14], and more accurate measurement of T1ρ requires more experiment data for both CP and DCP. Considering the practical systems with various I-S dipolar couplings, the QCP experiment is somewhat time-consuming especially when the systems contain multiple sites.
4 Quantitative CP with prolonged T1ρ relaxation timeAs seen, the quantitative CP methods discussed above were established under the shadow of the relaxation rates that is "intrinsic" characteristics of the spin system in practical spin systems. However, as it turned out, these characteristics could also be manipulated, with the application of decoupling or recoupling techniques[11, 33].
It was discovered that the Lee-Goldburg (LG) sequence[34] could significantly elongate the proton T1ρ by spin-locking the spins at the magic angle[33], as the homonuclear dipolar couplings were suppressed efficiently during the irradiation. Fu et al.[33] compared the relaxation times in rotating frame with spin lock in xy plane and at magic angle, i.e. normal on-resonance spin lock and LG spin lock, on a 15N-1, 3, 5, 7-labeled polypeptide, gramicidin A. This polypeptide was encapsulated by DPMC bilayers and dissolved in water. As a liquid crystal, the bilayer retained some structural anisotropy, and it was orientated parallel to the direction of B0 field. The 1H spin-lattice relaxation time in the rotating frame with the regular spin lock in xy plane was 3.51 ms, and prolonged to 7.37 ms under LG spin lock at the magic angle. It showed that the spin-lattice relaxation in the rotating frame along the magic angle was much slower than that in the xy plane. The LG spin lock was accomplished by firstly applying a 54.7° pulse, then followed by an off-resonance RF field irradiation. When the resonance offset Ω and RF power ω1 satisfy the equation:
| $ \omega_1 = \sqrt 2 \Omega $ | (5) |
an effective field:
| $ \omega_{\rm eff} = \sqrt {3/2} \omega_1 $ | (6) |
would lie on the magic angle. The high-order homonuclear Hamiltonian contributes to the T1ρ relaxation of 1H during the spin lock in xy plane, especially under relatively weak RF irradiation. While applying the LG spin lock, served as a homonuclear decoupling sequence, could completely suppress the first-order 1H-1H homonuclear dipolar Hamiltonian terms. As a result, the spin-lattice relaxation in the rotating frame at magic angle was less affected by the internal spin interactions, showing a slower T1ρ relaxation[33]. As discussed above, the polarization transfer during the CP contact is always benefiting from a slower T1ρ relaxation especially in the spin system with weak I-S dipolar coupling.
Fu et al.[11] modified the conventional CP by applying the LG spinlock on proton channel, while the carrier frequency of 15N RF field irradiation was modulated by a sine wave (LG-FMCP) as shown in Fig. 7(a), and the modulated carrier frequency on 15N channel could broaden the CP HH matching condition. On the sample of 15N-L-histidine, T1ρ of non-protonated 15N site were 13.6 ms and 28.9 ms for the regular on-resonance spin lock and LG spin lock along magic angle, respectively, indicating the LG irradiation slower the T1ρ relaxation by a factor of 2. Higher RF power had little effect for the on-resonance spin lock, but could result in longer T1ρ relaxation time in the LG-FMCP experiment. By applying the LG-FMCP method with a contact time of 8 ms, the intensities of protonated and non-protonated 15N signals could be improved by 20% and 27%, respectively, comparing to the regular CP/MAS spectrum. It should be noted that the buildup rates of 15N signal in LG-FMCP were slower than that in regular CP, as shown in Fig. 7(b) and 7(c), the corresponding scale-down factor was (1-λ) where
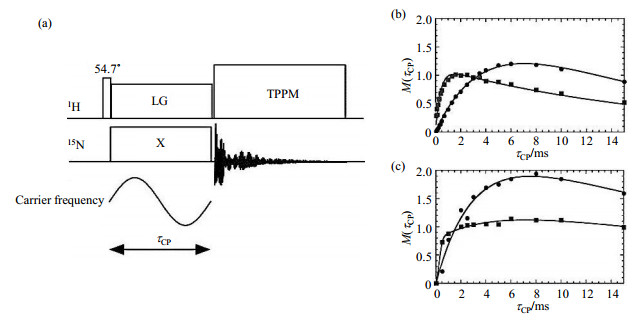
|
Fig. 7 (a) Pulse sequence of LG-FMCP, and 15N NMR signal buildup curves of 15N-L-histidine by (b) regular CP and (c) LG-FMCP methods. The solid circles and squares indicate the non-protonated and protonated 15N sites, respectively (Reproduced according to Ref. [11]) |
| $ \lambda = {T_{{\rm{NH}}}}/{T_{1\rho ,{\rm{H}}}} $ | (7) |
In other words, the prolonged T1ρ relaxation time increased the efficiency of polarization transfer while simultaneously slower the transfer rate[11].
5 Spin diffusion driven quantitative CPAs mentioned above, there exist two processes during the CP period, polarization transfer from abundant spin I to dilute spin S, and the spin diffusion among dilute spins. Since the polarization transfer rate is much higher than the spin diffusion rate, and also, the polarization buildup has to suffer from the relaxation effect, usually a non-uniform enhancement is obtained in the conventional CP spectroscopy. Series of additional delays were introduced in multiple-contact CP, letting the S spins diffuse the polarization to reach the same spin temperature[8]. Under MAS rotation, S-S homonuclear dipolar couplings are averaged out, and the spin diffusion might be slower in dilute spin S. Therefore, it is necessary to reintroduce the S-S homonuclear dipolar couplings by appropriate sequences.
Following the CP (either flat-CP or RAMP-CP) contact, an additional period with broadband homonuclear recoupling is applied prior to the acquisition, in the meanwhile the CP enhanced S signals can evolve to the final uniform enhancement [Fig. 8(a)], this method is named as QUCP[12]. The broadband homonuclear recoupling is accomplished by dipolar-assisted rotational resonance (DARR)[35]. Considering the rotational resonance recoupling[36] in 13C spin system for instance, the 13C-13C homonuclear recoupling can be reintroduced only when the MAS frequency
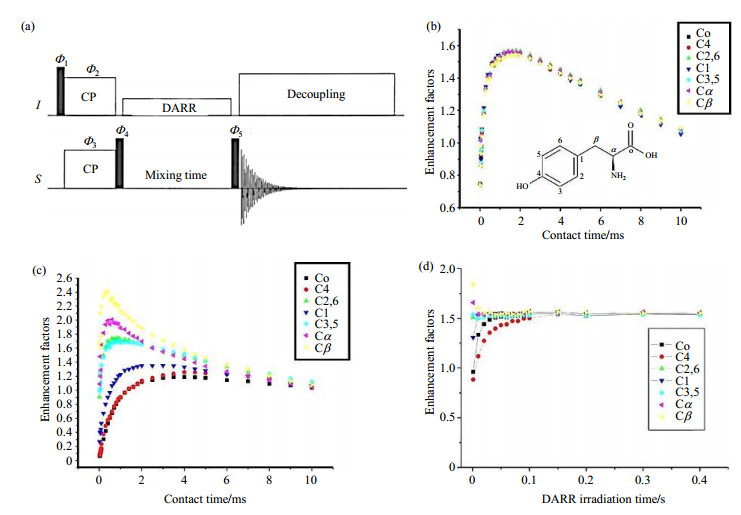
|
Fig. 8 (a) The QUCP pulse sequence and (b) the buildup curves of L-tyrosine, comparing to (c) the normal CP buildup curves. (d) The evolution of the signal enhancement factors as the increasing mixing time of the same sample. The experiments were carried out at a Varian Infinityplus-300 NMR spectrometer, with spinning speed of 12 kHz (Reproduced according to Ref. [12]) |
| $ n{\omega _r} = \Delta {\omega _{\rm{C}}} $ | (8) |
where
In the QUCP sequence, heteronuclear polarization transfer is accomplished via the conventional CP, and then the non-uniformly enhanced magnetization of S spins is tilted to the z direction, followed by an additional mixing period for spin diffusion among S spins. During the mixing time, a DARR irradiation is applied on I channel to reintroduce the homonuclear dipolar couplings among the S spins. The redistribution of polarization occurs among these non-uniformly enhanced S spins, rendering a quasiequilibrium state therefore consistent enhancement, which is significant for the quantitative NMR measurements. Although the final enhancement factor depends on the efficiency of the prior CP contact, the following spin diffusion driven by homonuclear recoupling sequence would always redistribute the magnetization of S spins to uniform enhancement. In other words, given sufficient mixing time, the consistency of enhancement in QUCP would be independent on the experimental parameters in CP[12, 13].
Even with the very sparse S spins, the uniform enhancement still can be reached, albeit longer recoupling time is needed. For instance, 13C single pulse, 1H-13C CP and QUCP NMR experiments had been carried out on natural abundant DL-alanine at a MAS frequency of 12 kHz[13]. The enhancement factors in each NMR experiment, normalized by the intensity of single pulse excitation with long pulse delay, were summarized in Table 2. No surprisingly, the enhancement factors for carbonyl/methyne/methyl carbons by CP deviated very much from the consistence. The QUCP NMR spectrum with mixing time of 5 s showed less deviations, but still non-uniform enhancement, which is mainly due to the very weak 13C-13C dipolar couplings in low 13C density system. The slow polarization transfer would require longer spin diffusion time to reach the quasi-equilibrium state. As demonstrated, QUCP with mixing time of 10 s resulted in the enhancement factors of 1.56, 1.57, 1.57 for three carbon groups, and a quantitative CP/MAS NMR spectrum was achieved (Table 2). In comparison to the quantitative NMR measurement by the direct excitation, an efficiency gain of 50 times was achieved by the QUCP approach[13]
| Table 2 The enhancement factors for 13C signal from natural abundant DL-alanine[13] |
In most quantitative solid-state NMR experiment, usually it's required that the optimized recycle delay is no less than 5 times of T1, where T1 denotes the spin-lattice relaxation time of dilute S spin when using the single pulse method, or that of abundant I spin when using CP-based quantitative NMR methods. Generally, T1 of the abundant I spin is much shorter than that of dilute S spin, but the NMR experiments with recycle delay of 5T1 can be time-consuming, and it should be noted that the spin-lattice relaxation time is required to be optimized prior to collecting quantitative NMR data.
It was discovered that, the feature of uniform enhancement in QUCP NMR experiments was not affected at all by the setting of recycle delay[15]. As demonstrated in 13C NMR spectra collected on 13C-labelled L-tyrosine spun at MAS frequency of 14 kHz, an uniform enhancement could not be achieved by the regular CP method whatever the recycle delay was (Fig 9). On the contrary, using the QUCP sequence with a mixing time of 1 s, the enhancement uniformity could be always achieved, although the recycle delay affected the value of final uniform enhancement factor, as shown in Fig. 9. The NMR results showed that the deviation of the enhancement factors was within ±0.02, allowing for quantitative analysis with high accuracy. Similarly, in natural abundant DL-alanine, the consistency of enhancement was also independent of the recycle delay, although a longer mixing time of 20 s was required[15]. The results indicated that the quantitative NMR measurements by QUCP would not be constrained by the relaxation time. The idea of breakthrough of T1 constraint in quantitative CP/MAS spectroscopy can be expanded into the quantitative NMR measurement by the direct excitation. Homonuclear dipolar recoupling technique, i.e. DARR, could also be placed prior to the 90° pulse excitation, which would accelerate the spin diffusion of spin system and recover in a uniform rate. Therefore, the recycle delay could be shortened in quantitative single pulse (QUSP) experiments, and the acquisition efficiency was improved[15].

|
Fig. 9 The 13C NMR spectra of 13C, 15N-L-tyrosine produced by (a) single pulse with 500 s recycle delay, (b, c) CP with recycle delay of 1 s and 15 s, (d, e) QUCP with recycle delay of 1 s and 15 s, respectively. And the enhancement factors of (f) CP and (g) QUCP as a function of recycle delay. All the spectra were recorded with 16 scan numbers, and were plotted on the same scale. The DARR possessed duration of 1 s, and the frequency was the same with MAS frequency, i.e., 14 kHz (Reproduced according to Ref. [15]) |
During the last two decades, tremendous development has been made on fast and ultra-fast MAS rotation technique in solid-state NMR[38]. With the availability of fast MAS frequencies up to 110 kHz, the spectral resolution can be improved greatly, and also, the proton reverse detection with high sensitivity would accelerate the data acquisition of multi-dimensional correlation spectroscopy. However, the implement of fast MAS technique brings up the NMR researchers new challenges, the demand for developing novel recoupling techniques suited for fast and ultra-fast MAS conditions[32, 39-42]. For instance, numerous pulse sequences have been proposed for achieving broadband homonuclear recoupling under fast MAS rates[32, 43-46]. In order to obtain quantitative CP/MAS spectrum under moderate-to-fast MAS rates (< 30 kHz), Takeda et al.[17] modified the QUCP sequence with phase-modulated SHA irradiation (Second-order Hamiltonian among Analogous Nuclei Generated by Hetero-nuclear Assistance Irradiation, SHANGHAI) as the replacement of DARR irradiation during the mixing period. As demonstrated, the phase modulated RF irradiation could more efficiently drive the spin diffusion among S spins to reach the final uniform enhancement.
6 Conclusion and outlookCP-based quantitative NMR methods provide us a powerful tool for obtaining accurate analysis of contents, component, and chemical sites in the practical systems with much higher sensitivity and acquisition efficiency. To achieve the quantification of CP/MAS spectroscopy, it is indispensable to accomplish consistent/uniform enhancement. The developed quantitative NMR methods started from multiple contact CP, including multiple-contact CP and multiCP, share the similar pulse sequence consists of a train of CP contacts. Within each CP contact, the magnetization of S spins is enhanced non-uniformly. An additional interval is applied between CP contacts, during the intervals I spins undergo the spin-lattice relaxation recovery and S spins undergo the spin diffusion process. Therefore, the reiteratively replenished polarization of I spins can further enhance the transfer to S spins, and the S spins evolve to a quasiequilibrium state. Repeated interval CP contacts could render the accumulation of signal intensity of detected spins, and reach, in theoretically, the maximum enhance factor of
| [1] | ENRST R R. Sensitivity enhancement in magnetic resonance[J]. Advances in Magnetic and Optical Resonance, 1966, 2: 1-135. DOI: 10.1016/B978-1-4832-3115-0.50008-9. |
| [2] | PINES A, GIBBY M G, WAUGH J S. Proton-enhanced NMR of dilute spins in solids[J]. J Chem Phys, 1973, 59(2): 569-590. DOI: 10.1063/1.1680061. |
| [3] |
WU X L, ZHANG S M. Polarization transfer in solid state CPMAS NMR[J].
Chinese J Magn Reson, 1995, 12(4): 429-438.
吴肖令, 张善民. 固态交叉极化魔角旋转NMR中的极化转移[J]. 波谱学杂志, 1995, 12(4): 429-438. |
| [4] |
DING S W, FU R Q, YE C H. Effects of non-secular terms in heteronuclear dipolar interaction on cross polarization relaxation rate[J].
Chinese J Magn Reson, 1993, 10(2): 123-130.
丁尚武, 傅日强, 叶朝辉. 异核偶极相互作用非久期项对交叉极化弛豫速率的影响[J]. 波谱学杂志, 1993, 10(2): 123-130. |
| [5] | LEVITT M H, SUTER D, ERNST R R. Spin dynamics and thermodynamics in solid-state NMR cross polarization[J]. J Chem Phys, 1986, 84(8): 4243. DOI: 10.1063/1.450046. |
| [6] | SHEKAR S C, LEE D K, RAMAMOORTHY A. Chemical shift anisotropy and offset effects in cross polarization solid-state NMR spectroscopy[J]. J Magn Reson, 2002, 157(2): 223-234. DOI: 10.1006/jmre.2002.2587. |
| [7] | PAULSON E K, MARTIN R W, ZILM K W. Cross polarization, radio frequency field homogeneity, and circuit balancing in high field solid state NMR probes[J]. J Magn Reson, 2004, 171(2): 314-323. DOI: 10.1016/j.jmr.2004.09.009. |
| [8] | ZHANG S M, WU X L, MEHRING M. Successive polarization under mismatched hartmann-hahn condition[J]. Chem Phys Lett, 1990, 166(1): 92-94. DOI: 10.1016/0009-2614(90)87056-W. |
| [9] | ZHANG S M, WU X L, ZHANG H P, et al. Quantitative measurement of rare spins in solid state cross polarization NMR[J]. Chem Phys Lett, 1990, 165(6): 465-468. DOI: 10.1016/0009-2614(90)87024-L. |
| [10] | METZ G, ZILIOX M, SMITH S O. Towards quantitative CP-MAS NMR[J]. Solid State Nucl Magn Reson, 1996, 7(3): 155-160. DOI: 10.1016/S0926-2040(96)01257-X. |
| [11] | FU R Q, HU J, CROSS T A. Towards quantitative measurements in solid-state CPMAS NMR:A Lee-Goldburg frequency modulated cross-polarization scheme[J]. J Magn Reson, 2004, 168(1): 8-17. DOI: 10.1016/j.jmr.2004.01.012. |
| [12] | HOU G J, DENG F, DING S W, et al. Quantitative cross-polarization NMR spectroscopy in uniformly 13C-labeled solids[J]. Chem Phys Lett, 2006, 421(4-6): 356-360. DOI: 10.1016/j.cplett.2006.01.105. |
| [13] | HOU G J, DENG F, YE C H, et al. Towards uniform enhancement in solid-state cross polarization magic[corrected] angle spinning NMR:a scheme incorporating cross polarization with rotational resonance[J]. J Chem Phys, 2006, 124(23): 234512. DOI: 10.1063/1.2206787. |
| [14] | SHU J, CHEN Q, ZHANG S M. Quantification of cross polarization with relaxation compensated reciprocity relation in NMR[J]. Chem Phys Lett, 2008, 462(1-3): 125-128. DOI: 10.1016/j.cplett.2008.07.026. |
| [15] | HOU G J, DING S W, ZHANG L M, et al. Breaking the T1 constraint for quantitative measurement in magic angle[J]. J Am Chem Soc, 2010, 132(16): 5538-5539. DOI: 10.1021/ja909550f. |
| [16] | TANG W X, NEVZOROV A A. Repetitive cross-polarization contacts via equilibration-re-equilibration of the proton bath:Sensitivity enhancement for NMR of membrane proteins reconstituted in magnetically aligned bicelles[J]. J Magn Reson, 2011, 212(1): 245-248. DOI: 10.1016/j.jmr.2011.06.028. |
| [17] | TAKEDA K, NODA Y, TAKEGOSHI K, et al. Quantitative cross-polarization at magic-angle spinning frequency of about 20 kHz[J]. J Magn Reson, 2012, 214(1): 340-345. |
| [18] | JOHNSON R L, SCHMIDT-ROHR K. Quantitative solid-state 13C NMR with signal enhancement by multiple cross polarization[J]. J Magn Reson, 2014, 239: 44-49. DOI: 10.1016/j.jmr.2013.11.009. |
| [19] | LIU H W, ZHOU X Y, CHEN Q, et al. Accurate quantitative and maximum cross polarization via multiple ramped contacts[J]. Chem Phys Lett, 2017, 679(1): 233-236. |
| [20] | LIU H W, ZHANG S M. Quantitative analysis of a labeled 13C system in NMR[J]. Chem Phys Lett, 2015, 621: 199-202. DOI: 10.1016/j.cplett.2014.12.050. |
| [21] | PEERSON O B, WU X L, KUSTANOVICH I, et al. Variable-amplitude cross-polarization MAS NMR[J]. J Magn Reson, Series A, 1993, 104(3): 334-339. DOI: 10.1006/jmra.1993.1231. |
| [22] | METZ G, WU X L, SMITH S O. Ramped-amplitude cross polarization in magic-angle-spinning NMR[J]. J Magn Reson, Series A, 1994, 110(2): 219-227. DOI: 10.1006/jmra.1994.1208. |
| [23] | COOK R L, LANGFORD C H, YAMDAGNI R, et al. A modified cross-polarization magic angle spinning 13C NMR procedure for the study of humic materials[J]. Anal Chem, 1996, 68(22): 3979-3986. DOI: 10.1021/ac960403a. |
| [24] | WU X L, ZHANG S M. Selective polarization inversion and depolarization of 13C in cross relaxation in NMR[J]. Chem Phys Lett, 1989, 156(1): 79-81. DOI: 10.1016/0009-2614(89)87085-X. |
| [25] | GERSTEIN B C, DYBOWSKI C R. Transient techniques in NMR of solids:an introduction to theory and practice[M]. San Diego: Academic Press, 1985. |
| [26] | RAYA J, PERRONE B, HIRSCHINGER J. Chemical shift powder spectra enhanced by multiple-contact cross-polarization under slow magic-angle spinning[J]. J Magn Reson, 2013, 227: 93-102. DOI: 10.1016/j.jmr.2012.12.006. |
| [27] | BROWNBILL N J, SPRICK R S, BONILLO B, et al. Structural elucidation of amorphous photocatalytic polymers from dynamic nuclear polarization enhanced solid state NMR[J]. Macromolecules, 2018, 51(8): 3088-3096. DOI: 10.1021/acs.macromol.7b02544. |
| [28] | KING C, STEIN R S, SHAMSHINA J L, et al. Measuring the purity of chitin with a clean, quantitative solid-state NMR method[J]. ACS Sustainable Chem Eng, 2017, 5(9): 8011-8016. DOI: 10.1021/acssuschemeng.7b01589. |
| [29] | SMET S, VERLOOY P, SAIDI F, et al. Solid-state NMR tools for the structural characterization of POSiSils:(29) Si sensitivity improvement with MC-CP and 2D (29) Si-(29) Si DQ-SQ at natural abundance[J]. Magn Reson Chem, 2019, 57(5): 224-229. DOI: 10.1002/mrc.4800. |
| [30] | WU X L, SHANMIN Z, XUEWEN W. Two-stage feature of Hartmann-Hahn cross relaxation in magic-angle sample spinning[J]. Phys Rev B Condens Matter, 1988, 37(16): 9827-9829. DOI: 10.1103/PhysRevB.37.9827. |
| [31] | SHU W F, ZHANG S M. Relaxation compensated and intensity recovered dynamics of cross polarization in the frame of reciprocity relation[J]. Chem Phys Lett, 2011, 511(4-6): 424-426. DOI: 10.1016/j.cplett.2011.06.037. |
| [32] | LU X Y, GUO C M, HOU G J, et al. Combined zero-quantum and spin-diffusion mixing for efficient homonuclear correlation spectroscopy under fast MAS:broadband recoupling and detection of long-range correlations[J]. J Biomol NMR, 2015, 61(1): 7-20. DOI: 10.1007/s10858-014-9875-6. |
| [33] | FU R Q, TIAN C L, CROSS T A. NMR spin locking of proton magnetization under a frequency-switched Lee-Goldburg pulse sequence[J]. J Magn Reson, 2002, 154(1): 130-135. DOI: 10.1006/jmre.2001.2468. |
| [34] | LEE M, GOLDBURG I W. Nuclear-magnetic-resonance line narrowing by a rotating RF field[J]. Phys Rev, 1965, 140(4A): 1261-1271. DOI: 10.1103/PhysRev.140.A1261. |
| [35] | TAKEGOSHI K, NAKAMURA S, TERAO T. 13C-1H dipolar-assisted rotational resonance in magic-angle spinning NMR[J]. Chem Phys Lett, 2001, 344(5): 634-637. |
| [36] | RALEIGH D P, LEVITT M H, GRIFFIN R G. Rotational resonance in solid state NMR[J]. Chem Phys Lett, 1988, 146(1, 2): 71-76. |
| [37] | OAS T G, GRIFFIN R G, LEVITT M H. Rotary resonance recoupling of dipolar interactions in solid-state nuclear magnetic resonance spectroscopy[J]. J Chem Phys, 1988, 89(2): 692-695. DOI: 10.1063/1.455191. |
| [38] | ZHANG R C, MROUE K H, RAMAMOORTHY A. Proton-based ultrafast magic angle spinning solid-state NMR spectroscopy[J]. Acc Chem Res, 2017, 50(4): 1105-1113. DOI: 10.1021/acs.accounts.7b00082. |
| [39] | CHEN L, WANG Q, HU B W, et al. Measurement of hetero-nuclear distances using a symmetry-based pulse sequence in solid-state NMR[J]. Phys Chem Chem Phys, 2010, 12(32): 9395-9405. DOI: 10.1039/b926546e. |
| [40] | TEYMOORI G, PAHARI B, VISWANATHAN E, et al. Multiple-quantum spin counting in magic-angle-spinning NMR via low-power symmetry-based dipolar recoupling[J]. J Magn Reson, 2013, 236: 31-40. DOI: 10.1016/j.jmr.2013.08.005. |
| [41] | HOU G J, YAN S, TREBOSC J, et al. Broadband homonuclear correlation spectroscopy driven by combined R2(n)(v) sequences under fast magic angle spinning for NMR structural analysis of organic and biological solids[J]. J Magn Reson, 2013, 232: 18-30. DOI: 10.1016/j.jmr.2013.04.009. |
| [42] | SHEN M, HU B W, LAFON O, et al. Broadband finite-pulse radio-frequency-driven recoupling (fp-RFDR) with (XY8)4(1) super-cycling for homo-nuclear correlations in very high magnetic fields at fast and ultra-fast MAS frequencies[J]. J Magn Reson, 2012, 223: 107-119. DOI: 10.1016/j.jmr.2012.07.013. |
| [43] | HU B W, LAFON O, TREBOSC J, et al. Broad-band homo-nuclear correlations assisted by 1H irradiation for bio-molecules in very high magnetic field at fast and ultra-fast MAS frequencies[J]. J Magn Reson, 2011, 212(2): 320-329. DOI: 10.1016/j.jmr.2011.07.011. |
| [44] | WEINGARTH M, DEMCO D E, BODENHAUSEN G, et al. Improved magnetization transfer in solid-state NMR with fast magic angle spinning[J]. Chem Phys Lett, 2009, 469(4-6): 342-348. DOI: 10.1016/j.cplett.2008.12.084. |
| [45] | HOU G J, YAN S, SUN S J, et al. Spin diffusion driven by R-symmetry sequences:applications to homonuclear correlation spectroscopy in MAS NMR of biological and organic solids[J]. J Am Chem Soc, 2011, 133(11): 3943-3953. DOI: 10.1021/ja108650x. |
| [46] | JAYANTHI S, AKBEY U, ULUCA B, et al. A floquet description of phase alternated sequences for efficient homonuclear recoupling in solid perdeuterated systems[J]. J Magn Reson, 2013, 234: 10-20. DOI: 10.1016/j.jmr.2013.05.007. |
 2019, Vol. 37
2019, Vol. 37 
