核磁共振(NMR)测量孔隙中的质子共振信号,在提供储层的孔隙度及孔隙结构信息方面具有独特优势[1].近年来,致密油、致密气、页岩气等非常规储层逐渐成为重要的勘探目标,岩心NMR分析及NMR测井在非常规储层中的应用也越来越多.由于非常规储层普遍呈现低孔、低渗特征,会加快质子弛豫,导致NMR测量信号强度降低.而测量参数,特别是回波间隔(TE)的合理选取可有助于提高信号强度和测量精度.
有研究[2, 3]表明,TE是影响NMR孔隙度(指的是NMR检测得到的表观孔隙度,下同)的主要因素,NMR孔隙度会随着TE的增大而减小.范宜仁等[4]通过不同孔隙度岩心NMR实验发现TE选择不合理会漏失一部分储层信息,降低短弛豫分量的分辨能力.Yan等[5]研究表明TE对微孔NMR信号检测起重要作用.很多学者研究了TE对页岩NMR测量结果的影响.高明哲等[6]研究不同TE值对页岩储层横向弛豫时间(T2)分布谱的影响时发现,随着TE的增大,T2谱左峰向右移动,且信号强度明显减弱,NMR孔隙度也明显减小.孙建孟等[7]研究了页岩粉碎样品的NMR特性,指出场强与主频较大的仪器拥有较小的TE和较高的信噪比,能够更加全面地反映页岩的微小孔隙特征.张涛等[8]分析了多种页岩孔隙度测量方法,指出NMR孔隙度测量值受TE影响,NMR孔隙度小于页岩真实孔隙度.Carl等[9]指出在测量页岩等小孔隙度储层样品时,要尽量选用短的TE.Aditya等[10]也发现使用较长的TE(> 0.114 ms)时,NMR孔隙度将低于页岩真实孔隙度.王志战等[11]研究发现,常用的NMR录井、测井仪器所使用的TE值可以精确评价常规储层,但在评价纳米孔储层时,应将TE缩小.
通过目前的研究可以获得的信息是:在NMR检测短T2组分时,大TE会导致信号漏失,应当尽量使用较小的TE.为了提高NMR技术在低孔低渗储层中的应用水平,还需要进一步研究以下两个问题:(1)由于TE对不同岩心NMR测量的影响存在差异,那么需要明确对某一特定岩心或储层,当TE大于多少时会对测量结果产生显著影响;(2)假如已经明确了某TE值下的测量结果与真实孔隙度存在偏差,如何进行合理的校正.
1 研究方法本文采用物理实验与数值模拟相结合的方法研究上述两个问题.NMR理论表明,岩心NMR测量结果可以看作该岩心内各种不同大小的孔隙的NMR行为的叠加,那么TE对测量结果的影响也可看作是TE对不同大小孔隙(对应特定的T2)NMR影响的叠加.因此,虽然实际测得的储层的T2谱是具有多个T2值的连续分布,但在后面的实验及数值模拟中,采用了单峰型T2谱的模拟样品或数值模型,以便于结果分析和定量研究影响规律.
1.1 NMR实验为了研究TE对不同大小的孔隙的影响规律,本文采用具有特定T2的三组CuSO4溶液模拟三种具有不同大小的孔隙的样品.由于TE对NMR测量结果的影响主要集中在小孔、微孔部分,而对尺寸较大孔隙的影响很小,因此,通过调节CuSO4溶液的浓度,配制了T2分别为0.5 ms、5 ms和40 ms的三组溶液各10 mL(以下简称1~3号)作为实验样品(图 1).

|
图 1 本文使用的T2值分别为40 ms、5 ms和0.5 ms的CuSO4溶液(从左至右) Fig. 1 CuSO4 solutions with T2 values of 40 ms, 5 ms and 0.5 ms used in this research(From left to right) |
采用MicroMR02-050V型岩心NMR分析仪,其磁场强度为(0.055±0.01)T,共振频率为2 MHz,该仪器采用GPMG序列测量T2时,回波个数最大为18 000个,最小TE为0.06 ms.对上述三组样品均进行了多TE值时的NMR测量,获得其不同TE下的回波信号.现有研究[11]表明,随着孔隙度及孔隙尺寸的降低,对NMR测量结果产生显著影响的TE逐渐降低.因此,对于具有相对较短T2的1号样品,TE分布范围选在0.1~4.0 ms,而对具有相对较长T2的3号样品,TE分布范围选在2.0~100 ms.详细的参数见表 1所示.共获得三个样品不同TE下的回波信号24组,对获得的回波信号进行T2谱反演,可以获得三个样品不同TE下的T2分布谱,进而研究TE对不同弛豫组分的影响规律.
| 表 1 不同TE下,三组CuSO4溶液的NMR测量参数 Table 1 NMR measurement parameters for the three CuSO4 solutions with variable TE values |
考虑到样品及实际测量次数的局限性,本文采用数值模拟方法模拟了不同尺寸的孔隙在不同TE下的NMR特性.数值模拟主要包括三个步骤:首先通过数学方法构造具有特定T2的单峰型T2谱,以模拟特定大小的孔隙(即特定弛豫组分);然后通过正演模拟其不同采集参数下的弛豫特性并获得自旋回波信号;最后对回波信号反演得到特定弛豫组分、特定采集参数下的T2谱.
数值模拟中采用对数坐标下的一维高斯分布公式构造T2谱:
| ${A_j} = \sum\limits_{g = 1}^n {{F_g}} {H_g}\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\sigma _g}} }}\exp \left[ { - \frac{{{{(\ln {T_{2j}} - \ln {T_{2g,{\rm{mid}}}})}^2}}}{{2\sigma _g^2}}} \right],{\rm{ }}j = 1,2, \cdots ,m$ | (1) |
(1) 式中,假设存在具有不同T2的n组孔隙,Fg是第g种孔隙的孔隙度分量,Hg是第g种孔隙中流体的含氢指数,T2g, mid是第g种孔隙的T2谱中心值,σg是第g种孔隙T2峰值的中心展布宽度,将T2谱对数均分为m种组分,T2j为第j种组分的横向弛豫时间,Aj为构造谱第j种弛豫组分对应的幅度值.
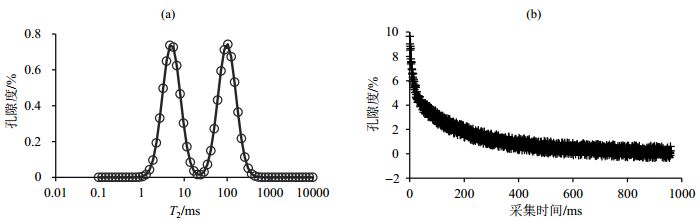
图 2(a)给出了构造两种不同弛豫组分的T2谱示例.对上述构造的T2谱通过正演模拟NMR测量.在均匀磁场下利用CPMG脉冲序列测量T2弛豫信号,若等待时间(TW)足够长,样品的自旋回波信号为[12]:
|
图 2 (a) 构造的具有两种不同弛豫组分的T2谱;(b)数值模拟回波串采集示例 Fig. 2 (a)Simulated T2 distribution spectra with two different relaxation components; (b)Numerical simulation of echo string acquisition |
| ${Y_i} = \sum\limits_{j = 1}^m {{f_j}\left[ {1 - \exp ( - \frac{{{T_{\rm{W}}}}}{{{T_{1j}}}})} \right]\exp (} - \frac{{{t_i}}}{{{T_{2j}}}})\times \exp ( - \frac{{{\gamma ^2}{G^2}T_{\rm{E}}^2D{t_i}}}{{12}})+ {\varepsilon _i},{\rm{ }}i = 1,2, \cdots ,n$ | (2) |
(2) 式中,m是T2弛豫组分数目,γ是旋磁比,G是磁场梯度,D是扩散系数,n是回波采集个数,Yi是采集到的第i个回波的幅度,ti是第i个回波对应的衰减时间,fj是T2为T2j分量的信号幅度,εi是噪音,T1j是第j种弛豫组分的纵向弛豫时间.图 2(b)是针对图 2(a)所示T2分布谱(对应着特定的弛豫组分)进行数值模拟得到的回波串.
反演方法本质上是在求解第一类Fredholm积分方程,对于此方程的求解,众多学者发展了许多算法,本文采用经典的奇异值分解(SVD)法,利用(3)式进行求解,得到T2谱[13].
| ${Y_t} = \sum\limits_{j = 1}^m {{f_j}\exp (} - \frac{t}{{{T_{2j}}}})$ | (3) |
(3) 式中,m是T2弛豫组分数目,
图 3是使用不同参数对图 2(b)所示数值模拟回波串反演得到T2谱.通过对比分析可以看出,数值模拟结果反演得到的T2谱(图 3)与模拟中采用的具有特定弛豫组分的数值模型非常相近,这说明采用(1)式和(2)式进行数值模拟是可行的.

|
图 3 使用不同参数数值模拟反演得到T2谱 Fig. 3 T2 spectra simulated by inversion using different parameters |
为了进一步验证上述数值模拟方法的可靠性和准确性,本文构造了与前述三组CuSO4溶液具有相同T2的数值模拟模型,即利用(1)式构造了T2分别为0.5 ms、5 ms和40 ms的三个单峰型T2谱.然后对每个模型采用一组与前述实验相同的模拟参数(表 2),利用(2)式进行CPMG脉冲序列弛豫特性模拟,获得三个样品的自旋回波信号,最后进行了三组回波信号的T2谱反演.
| 表 2 数值模拟可靠性验证的模拟参数 Table 2 Simulated parameters for numerical simulation reliability verification |
图 4(a)对比了三组CuSO4溶液NMR实验获得的回波串及相同参数下数值模拟获得的回波串,图 4(b)对比了对上述两组回波串反演获得的T2谱.从图中可以看出,无论是回波串,还是T2谱形态、峰值位置和包络线面积(孔隙度),数值模拟与NMR实验结果都很接近,这进一步验证了文章所采用数值模拟方法的可靠性和准确性.

|
图 4 CuSO4 NMR实验结果与数值模拟对比.(a)回波串;(b)T2谱 Fig. 4 Comparisons between NMR experimental results and numerical simulation results of CuSO4 solutions. (a)Echo string; (b)T2 distribution |
NMR实验时对三种CuSO4溶液进行了8种不同TE下共24次测量(表 1).数值模拟中,首先利用1.2节介绍的方法构造了32组单峰型T2谱的数值模拟模型,这些模型的T2值在0.01~10 000 ms之间按照相同倍数逐渐变化.然后对每个模型在0.04~40 ms之间采用32个不同TE值分别进行弛豫模拟,共获得1 024(32×32)组回波串及反演后的T2谱.
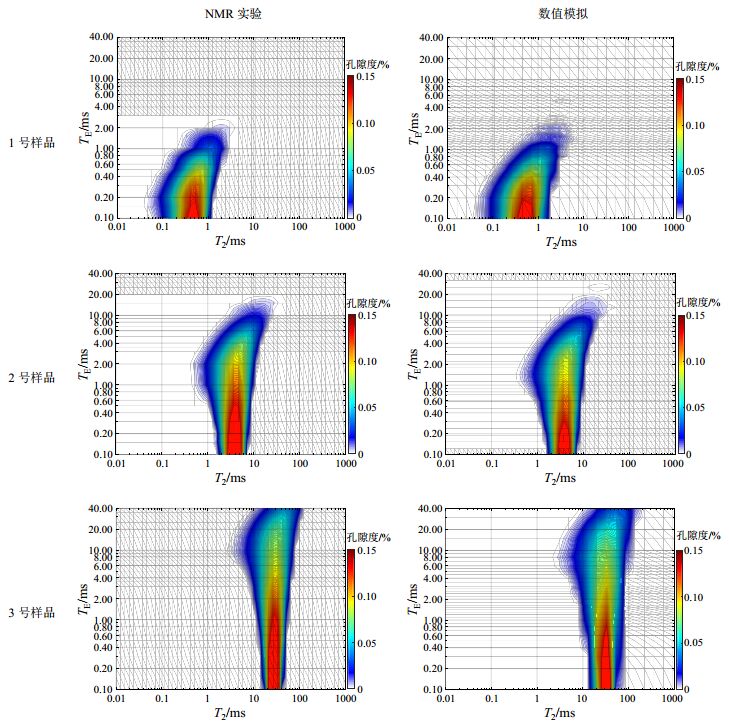
1号样品的T2为0.5 ms,从该样品的NMR实验结果及对应的数值模拟结果(图 5第一行)可知:TE从0.1 ms逐渐增大到2 ms过程中,T2谱峰值位置逐渐右移且包络面积减小,当TE > 2 ms后,几乎检测不到任何弛豫信号.2号样品T2约为5 ms,其NMR实验及模拟结果与1号样品的规律相似,只是当TE > 0.4 ms之后,弛豫信号才有明显的衰减.由3号样品实验结果和其对应的数值模拟结果可以看到,即使当TE达到20 ms,仍有弛豫信号能够被采集到.
|
图 5 CuSO4溶液变TE的NMR测量结果和对应的数值模拟结果 Fig. 5 NMR measurements of CuSO4 solutions with variable TE and corresponding numerical simulations |
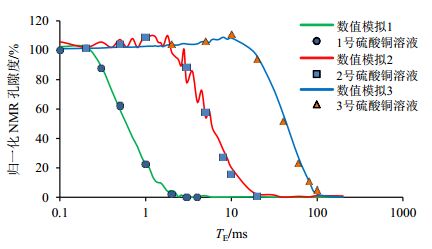
从图 5可以看出,TE对回波信号采集及T2谱具有显著影响,但对不同样品(具有不同孔隙结构及弛豫组分)产生显著影响的TE值存在差异.为了进一步定量分析TE对测量结果的影响,图 6给出了三个样品归一化NMR孔隙度(即NMR孔隙度与气测孔隙度的比值)随TE的变化规律.从图 6可以看出,不同样品归一化NMR孔隙度随TE变化的总体趋势一致:随着TE的增大,各弛豫组分归一化NMR孔隙度先维持在100%左右不变;至某TE时,迅速衰减;最后当TE增加到一定数值时,衰减为0.但不同弛豫组分归一化NMR孔隙度开始迅速衰减及最后变为0的TE值存在显著差异,而且这两个TE值随着弛豫组分T2值的增大而增大.
|
图 6 三个CuSO4样品的归一化NMR孔隙度与TE的关系 Fig. 6 Relationship between normalized NMR porosity and TE values of the three CuSO4 solutions |
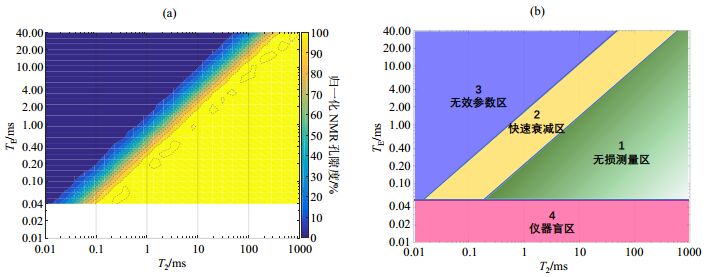
为了定量描述T2弛豫组分损失与TE之间的关系,将32组变TE测量得到的归一化NMR孔隙度值矩阵绘制成32×32的等高线图[图 7(a)],其中,横坐标是不同组分的T2,纵坐标是测量时采用的TE,不同的颜色则代表归一化NMR孔隙度.归一化NMR孔隙度越小表明对应T2弛豫组分在该TE值下损失越多.利用图 7可以分析出对于某一特定的T2弛豫组分(与特定孔隙组分对应),其T2测量损失程度随TE的变化规律.例如:对于T2为10 ms的组分,当TE < 2 ms时,归一化NMR孔隙度接近100%,弛豫组分完全没有损失;当TE > 2 ms后,归一化NMR孔隙度迅速减小;若TE > 8 ms,T2为10 ms组分将全部损失.
|
图 7 (a) 不同T2弛豫组分归一化NMR孔隙度与TE的关系;(b) T2弛豫组分与测量参数分区 Fig. 7 (a)Relationship between normalized NMR porosity and TE values of components with different T2 values; (b)T2 relaxation components and measurement parameters zoning |
为了更好地确定NMR实验和NMR测井的TE,从而提高测量结果的准确度,根据不同T2弛豫组分归一化NMR孔隙度与TE的关系,将整个NMR测量分为4个区域:无损测量区、快速衰减区、无效参数区和仪器盲区[图 7(b)].从图 7(b)可以看出,当选择的TE值处于无损测量区时,可以测得完整T2谱,计算的NMR孔隙度没有损失;当TE值处于快速衰减区时,可以测得部分T2谱,NMR孔隙度小于真实孔隙度,必须进行适当的校正;当TE值处于无效参数区时,无法获取正确的T2信号,NMR孔隙度结果是错误的;仪器盲区则受所使用的NMR仪器参数指标限制,不同仪器其盲区大小不同.
2.3 快速衰减区NMR孔隙度校正方法由图 7可以看出,当T2接近0.1 ms时,即使采用目前岩心NMR分析仪TE的下限(约0.06 ms),测量结果也将处于快速衰减区,此时必须对NMR孔隙度进行校正才能得到正确的结果.图 8是孙建孟等[7]在不同磁场强度、不同TE值下对页岩岩心的测量结果,是一个典型的处于快速衰减区的案例,必须对NMR孔隙度进行校正.

|
图 8 NMR孔隙度与TE之间的关系(依据文献[7]修改) Fig. 8 Relationship between NMR porosity and TE (Reproduced from Ref. [7]) |
图 9是特定T2组弛豫组分(0.5 ms)的NMR孔隙度损失率与TE的关系曲线.从图中可以看到,随着TE的增大,孔隙度损失率显著增加.定量分析表明,对某一特定T2弛豫组分,孔隙度损失率与TE具有很好的对数相关性,为了获得准确的NMR孔隙度,可以利用下面的公式进行校正(具体推导过程参见网络版附件或扫描该文章首页OSID码查看附件):

|
图 9 NMR孔隙度损失率与TE的关系(T2=0.5 ms) Fig. 9 Relationship between NMR porosity loss rate and TE(T2=0.5 ms) |
| ${P_{{\rm{NMR}}}} = \frac{{{P_a}}}{{a\ln {T_{\rm{E}}} + b}}$ | (4) |
(4) 式中,PNMR是校正后的NMR孔隙度,Pa是校正前的NMR孔隙度,a、b为模型参数.对于该校正方法,至少需要有两组以上不同TE的测量数据,以确定参数a、b的值.
图 10是实验室使用TE分别0.1 ms、0.6 ms(一维NMR测井常用TE[14])的测量结果,NMR孔隙度分别是10.74%和7.49%,差别较大,原因是此岩心主峰位置在0.1~5 ms,采用0.6 ms的TE导致T2 < 3 ms的弛豫组分均落在了快速衰减区.对TE为0.6 ms的测量结果逐组分进行校正后,NMR孔隙度达到了9.44%,和10.74%较为接近.

|
图 10 NMR孔隙度校正效果 Fig. 10 Correction effect of NMR porosity |
(1)随着TE的变化,不同T2弛豫组分归一化NMR孔隙度呈现相似的变化规律:当TE值比较低时,归一化NMR孔隙度维持在100%左右不变;当TE大于某一数值时,迅速衰减,当TE增加到一定数值时,衰减为0.但不同T2弛豫组分归一化NMR孔隙度开始迅速衰减及最后变为0的TE值存在显著差异.
(2)根据T2弛豫组分损失与TE的定量关系,可以把整个NMR测量分为无损测量区、快速衰减区、无效参数区和仪器盲区4个区域.当TE落在快速衰减区时,NMR仪器无法测得完整的T2弛豫信号,NMR孔隙度小于真实孔隙度,必须进行适当的校正.在快速衰减区弛豫组分损失量与TE呈对数关系.
本文仅对NMR孔隙度的校正方法进行了分析,T2谱形态和位置的校正是下一步的研究方向.
| [1] | PRAMMER M G, DRACK E D, BOUTON J C, et al. Measurements of clay-bound water and total porosity by magnetic resonance logging[C]. Colorado: SPE Annual Technical Conference and Exhibition, Formation Evaluation and Reservoir Geology, 1996: 311-320. 10.2118/36522-MS |
| [2] |
WANG W M, YE C H, GUO H K. Experimental studies of NMR properties of continental sedimentary rocks[J].
Chinese J Magn Reson, 2001, 18(2): 113-121.
王为民, 叶朝辉, 郭和坤. 陆相储层岩石核磁共振物理特征的实验研究[J]. 波谱学杂志, 2001, 18(2): 113-121. DOI: 10.3969/j.issn.1000-4556.2001.02.003. |
| [3] |
WANG Z D, WANG H, LI N G, et al. Analysis of core NMR data from laboratory measurements[J].
Well Logging Technology, 2001, 25(3): 170-174.
王忠东, 汪浩, 李能根, 等. 核磁共振岩心基础实验分析[J]. 测井技术, 2001, 25(3): 170-174. DOI: 10.3969/j.issn.1004-1338.2001.03.003. |
| [4] |
FAN Y R, NI Z G, DENG S G, et al. Experimental study on NMR measurement parameters and reservoir properties[J].
Petroleum Geology & Experiment, 2005, 27(6): 624-626.
范宜仁, 倪自高, 邓少贵, 等. 储层性质与核磁共振测量参数的实验研究[J]. 石油实验地质, 2005, 27(6): 624-626. DOI: 10.3969/j.issn.1001-6112.2005.06.014. |
| [5] | YAN W C, SUN J M, SUN Y, et al. A robust NMR method to measure porosity of low porosity rocks[J]. Microporous and Mesoporous Materials, 2018, 269: 113-117. DOI: 10.1016/j.micromeso.2018.02.022. |
| [6] |
GAO M Z, ZOU C C, PENG C, et al. Study on selection method of core nuclear magnetic experiment parameters for shale reservoir[J].
Chinese Journal of Engineering Geophysics, 2016, 13(3): 263-270.
高明哲, 邹长春, 彭诚, 等. 页岩储层岩心核磁共振实验参数选取方法研究[J]. 工程地球物理学报, 2016, 13(3): 263-270. DOI: 10.3969/j.issn.1672-7940.2016.03.002. |
| [7] |
SUN J M, ZONG C L, DONG X, et al. Porosity measurement of crushed shales using NMR[J].
Well Logging Technology, 2017, 41(5): 512-516.
孙建孟, 宗成林, 董旭, 等. 基于核磁共振的页岩粉碎样品孔隙度研究[J]. 测井技术, 2017, 41(5): 512-516. |
| [8] |
ZHANG T, ZHANG X W. Comparative study on qualitative and quantitative methods for shale pore characterization[J].
Natural Gas Exploration and Development, 2017, 40(4): 34-43.
张涛, 张希巍. 页岩孔隙定性与定量方法的对比研究[J]. 天然气勘探与开发, 2017, 40(4): 34-43. |
| [9] | SONDERGELD C, TINNI A, RAI C, et al. NMR considerations in shale evaluation[C]//Spwla-2016-rrr, [S.l.]: Society of Petrophysicists and Well-log Analysts, 2016: 9. https://www.onepetro.org/conference-paper/SPWLA-2016-RRR |
| [10] | CHAKRAVARTY A, TINNI A, RAIC C S, et al. NMR considerations in shales at elevated temperature[C]. Texas: SPE/AAPG/SEG Unconventional Resources Technology Conference. Houston, 2018. 10.15530/urtec-2018-2902883 |
| [11] |
WANG Z Z, LI X, WEI Y X, et al. NMR technologies for evaluating oil & gas shale:a review[J].
Chinese J Magn Reson, 2015, 32(4): 688-698.
王志战, 李新, 魏杨旭, 等. 页岩油气层核磁共振评价技术综述[J]. 波谱学杂志, 2015, 32(4): 688-698. |
| [12] |
XIE R H, XIAO L Z, LIU J J, et al. A method for multiple echo trains jointing inversion of NMR relaxing measurements[J].
Chinese Journal of Geophysics, 2009, 52(11): 2913-2919.
谢然红, 肖立志, 刘家军, 等. 核磁共振多回波串联合反演方法[J]. 地球物理学报, 2009, 52(11): 2913-2919. |
| [13] |
JIANG R Z, YAO Y P, MIAO S, et al. Improved algorithm for singular value decomposition inversion of T2 spectrum in nuclear magnetic resonance[J].
Acta Petrolei Sinica, 2005, 26(6): 57-59.
姜瑞忠, 姚彦平, 苗盛, 等. 核磁共振T2谱奇异值分解反演改进算法[J]. 石油学报, 2005, 26(6): 57-59. |
| [14] |
ZHANG S M, ZHANG S N, GE X, et al. Optimal design and application of two-dimensional NMR logging in Chuanxi tight gas reservoir[J].
Chinese J Magn Reson, 2018, 35(2): 234-242.
张世懋, 张哨楠, 葛祥, 等. 川西致密气藏二维核磁共振测井优化设计与应用[J]. 波谱学杂志, 2018, 35(2): 234-242. |
 2020, Vol. 37
2020, Vol. 37 
