2. IMDEA Nanoscience, Faraday 9, Ciudad Universitaria de Cantoblanco, Madrid 28049
2. IMDEA Nanoscience, Faraday 9, Ciudad Universitaria de Cantoblanco, Madrid 28049, Spain
由于拥有可剥离、可离子交换的层状结构,Mg/Al双金属氢氧化物已受到了广泛关注,并在吸附剂、药物稳定剂、生物活性纳米复合材料、催化材料前体等诸多方面展现出了潜在应用价值[1-4].为了进一步提高其性能,研究者们开始寻找在其他金属氢氧化物中是否存在类似的层状结构,其中一个研究热点是将稀土元素和层状氢氧化物相结合,构建由稀土阳离子配位多面体互相连接而成的层状稀土氢氧化物(layered rare earth hydroxide).稀土元素包括15种镧系元素和IIIB族的钪和钇,由于其独特的4f电子构型,稀土化合物往往具有优良的光学、磁学和催化等特性.层状稀土氢氧化物既保留了常规层状金属氢氧化物的优点,又综合了稀土元素本身的功能性,从而成为了一类新型且性能优越的稀土功能材料[5-7].
在层状稀土氢氧化物中,组成为RE(OH)2NO3(RE表示稀土元素)的化合物在水热条件下可以发生离子交换[8].近年来,研究发现该化合物还具有非线性光学特性,其在紫外-可见光区的二次谐波效应强度达到了磷酸二氢钾的5倍以上,并且在紫外至近红外区都具有很高的透光性和双折射率,是颇具潜力的非线性光学材料[9].早期的X射线衍射(X-ray diffraction,XRD)数据显示该化合物属于中心对称的空间群P21/m[10, 11],与实验中观测到的非线性光学特性不符,因此最新的单晶XRD数据将其解析为非中心对称的空间群P21[9].值得注意的是,层状金属氢氧化物的结构往往存在争议.这一类化合物中二维层的堆叠相对比较均一,但是由于层状金属氢氧化物中二维层之间通过弱相互作用连接,不同层之间很可能存在一定程度的滑移,产生不同的堆叠方式,这是XRD技术所难以分辨的.除此之外,层状稀土氢氧化物中存在着大量的氢原子,这些氢原子的位置很难通过XRD技术确定,而它们可以影响晶体的对称性.因此,RE(OH)2NO3的结构需要通过与XRD技术互补的其他表征手段进行确定.固体核磁共振(solid state nuclear magnetic resonance,SSNMR)技术是对衍射技术的有效补充,它对短程有序的结构比较敏感,可以通过测得的NMR谱图分析得到稀土原子周围的配位信息,如配位数、配位原子种类、配位壳层的几何构型等[12-15].与此同时,通过SSNMR实验也可以获得长程有序的信息,例如空间群,因为从理论上说NMR谱峰的数目等于结构中晶体学不等同位点的数目,而谱峰的强度比等于结构中晶体学不等同位点的数量比[16-18].
本文通过SSNMR技术研究层状La(OH)2NO3化合物.在镧的两种天然同位素(138La和139La)中,139La具有较为优良的NMR特性:半整数自旋量子数(I = 7/2)、非常高的天然丰度(99.91%)、中等旋磁比(9.4 T下的共振频率约为56.9 MHz)和中等核四极矩(0.20 Barn,1 Barn=1×10−28 m2)[19, 20].尽管如此,获取139La SSNMR谱图仍然是一个很大的挑战,因为La3+往往具有很高的配位数(> 6),使得其配位壳层几何构型远离球对称,导致由139La四极相互作用中心跃迁引起的谱图展宽往往超过数百千赫兹.在这种情况下,常规的魔角旋转实验无法有效分离旋转边带,产生的谱图线型非常复杂,难于分析.而在静态实验中,139La NMR信号在很宽的范围内分布,谱图信噪比很低.除此之外,由四极作用引起的139La快速弛豫和射频脉冲有限的激发宽度都会导致139La SSNMR谱图采集出现问题.其中谱图低信噪比的问题可以通过使用四极核CPMG(quadrupolar Carr-Purcell-Meiboom-Gill,QCPMG)脉冲序列解决[21-23],但是此时获取的单片谱图线型扭曲严重,并且只覆盖了超宽谱的很小一部分.结合变频谱图采集方法之后[24],可以获取一系列频率步进分片NMR谱,将它们叠加之后就可以形成完整的超宽NMR谱.对谱图进行模拟之后就可以从中获得139La NMR参数,对其进行分析可得到晶体对称性和镧氧多面体配位构型等结构信息.
1 实验部分 1.1 样品合成和表征La(OH)2NO3的合成:首先将4 mol/L的分析纯La(NO3)3·6H2O溶于2 mL去离子水,加热至65 ℃,然后边搅拌边缓慢滳加4 mL浓度为4 mol/L的分析纯NaOH水溶液,直至完全混合.将生成的白色胶体转移至高压反应釜中,在150 ℃下加热18 h,得到的白色产物在常温下用去离子水清洗3~5次,然后在60 ℃下烘干,即可得到纯净的La(OH)2NO3样品.
粉末XRD实验:实验所用粉末XRD仪器型号为Rigaku SmartLab,X射线源为铜靶Kα辐射(λ = 0.154 06 nm),扫描速度为10°/min,扫描范围为5° ≤ 2θ ≤ 60°,步进值为0.02°.
139La SSNMR实验:静态SSNMR实验在9.4 T下进行,机柜型号为Bruker Avance IIIHD,使用4 mm Bruker商用双通道魔角旋转探头,此时139La的拉莫尔频率约为56.54 MHz.在氯化镧水溶液上测得的139La核90°脉冲宽度为5.25 μs,对应的中心跃迁选择脉冲宽度为1.31 μs的90°脉冲,氯化镧水溶液同时作为139La NMR化学位移的定标样品(δiso 0).由于139La NMR谱的宽度可以达到几兆赫兹的宽度,远远超出现有探头90°脉冲的最大激发宽度(约200 kHz),因此使用了变频谱图采集方法.在这一方法中,载波频率按照相同的步进值逐渐增加(或减少),从而获得一系列分片NMR谱,将这些分片NMR谱进行叠加就可获得整张超宽139La SSNMR谱.本文使用了QCPMG脉冲提高单片SSNMR谱图的信噪比,其中QCPMG循环周期长度为400 μs,QCPMG循环周期数目为81,扫描次数为1 024,扫描间隔为0.5 s,使用TPPM序列进行质子去耦,测得的数据通过NUTS2005软件进行谱图重构,并采用QUEST软件对其进行拟合[23, 25, 26].本文分片NMR谱的谱宽为1.25 MHz,相邻分片NMR谱的载波频率步进值为100 kHz,整张超宽139La SSNMR谱由86张分片NMR谱叠加而成.
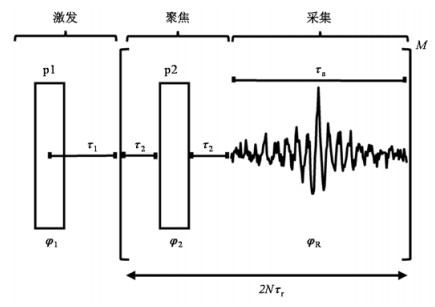
1.2 QCPMG脉冲序列QCPMG脉冲序列已被广泛用于获取各类四极核的SSNMR谱图.如图 1所示,QCPMG脉冲序列由激发单元、聚焦单元和采集单元组成,后两者合称为一个QCPMG循环[23].在魔角旋转实验中,QCPMG循环周期的长度应等于魔角旋转周期τr的2N倍,其中N为整数.在QCPMG实验中,139La被脉冲p1(通常为中心跃迁,选择90°脉冲)激发后,产生的信号经过脉冲p2(通常为中心跃迁,选择180°脉冲)聚焦,在采集单元中收集到完整的自旋回波信号,接下来QCPMG循环重复M次,使得单个自由感应衰减(free induction decay,FID)数据中包含了一系列的自旋回波数据.如果对FID数据直接进行傅里叶变换,得到的谱图是由间距为QCPMG循环周期倒数[即1/(2Nτr),以Hz为单位]的诸多“类旋转边带”所组成,由“类旋转边带”顶点连接而成的包络图与常规粉末谱图的形状相同.此时由于NMR信号集中在“类旋转边带”之中,其信噪比得到了大幅增强.如果先将QCPMG FID数据中的一系列自旋回波数据进行叠加,然后进行傅里叶变换,得到的谱图与常规粉末谱图的形状相同,但是叠加之后的自旋回波数据信噪比显著高于单个自旋回波数据,重建后的谱图信噪比仍然得到了大幅提升[22].
|
图 1 QCPMG脉冲序列:p1为激发脉冲;p2为聚焦脉冲;τa为数据采集期;2Nτr为QCPMG循环周期;τ1、τ2为脉冲间隔;φ1、φ2、φR为相位 Fig. 1 QCPMG pulse sequence: p1 is the excitation pulse; p2 is the refocusing pulse; τa is the acquisition length; 2Nτr is the QCPMG cycle; τ1 and τ2 are interpulse delays; φ1, φ2, and φR are phases |
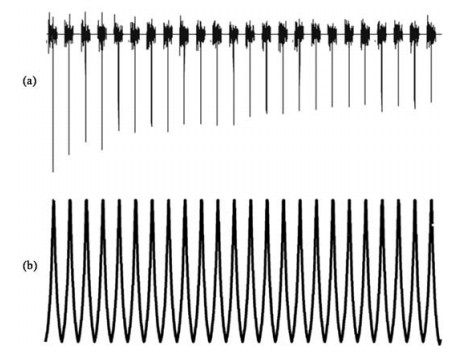
如图 2(a)所示,QCPMG实验中获取的FID数据中包含一系列自旋回波数据,如果不进行叠加,当使用常规滤波方程(或窗口方程)进行谱图处理时,信号和噪音同时衰减,导致在使用大线宽因子(line broadening,LB)时带来的信噪比优势并不明显,反而显著降低了谱图分辨率.图 2(b)展示了适用于QCPMG实验的滤波方程,它是由一些周期性的洛伦兹线型构成,顶点高度为1,其他点的高度随与顶点之间的距离增加而迅速降低[22].滤波过程中,自旋回波顶点与滤波方程顶点对齐之后两者相乘,使得自旋回波信号衰减很小,而噪音大幅衰减,从而很好的提高了谱图的信噪比.
|
图 2 (a) QCPMG实验中获取的典型FID数据;(b)本文使用的适用于QCPMG实验的滤波方程线型 Fig. 2 (a) A typical FID data acquired in QCPMG experiments; (b) A schematic illustration of the filter for QCPMG experiments in this work |
本文采用Materials Studio软件自带的Cambridge Sequential Total Energy Package(CASTEP)对层状La(OH)2NO3化合物(P21或P21/m结构)进行了密度泛函理论计算,因为CASTEP在周期性边界条件下工作,对三维晶体的性质预测往往能取得优于基于常规团簇模型的计算结果[27].计算过程中,密度泛函为PBE,SCF收敛判据、k点数目等使用了CASTEP内置的“coarse”、“medium”或“fine”判据,由于镧为重元素,因此使用了相对论效应校正(Schroedinger、Koelling-Harmon或ZORA)进行计算.先保持晶胞参数不变,对P21晶体结构中的所有原子位置进行了优化,随后在优化后晶体结构的基础上进行了“NMR”计算,得到了139La四极耦合常数CQ和非对称因子ηQ.P21/m结构对应的晶体学文件中缺少氢原子位置,并且存在占位率只有一半的一个氮位点和一个氧位点[11].为了解决这一问题,本文对晶体学文件进行了如下处理:首先在羟基氧上添加了氢原子,随后将晶体对称性降低为P1,并且删除原晶体学文件中由于存在对称镜面而产生的额外氮原子和氧原子.以得到的晶体结构为基础,优化所有原子的位置,进行“NMR”计算,获取139La四极耦合常数CQ和非对称因子ηQ.
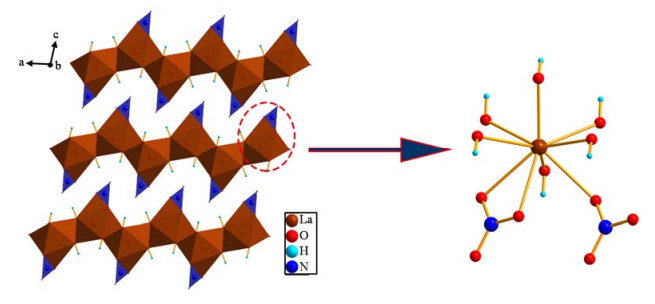
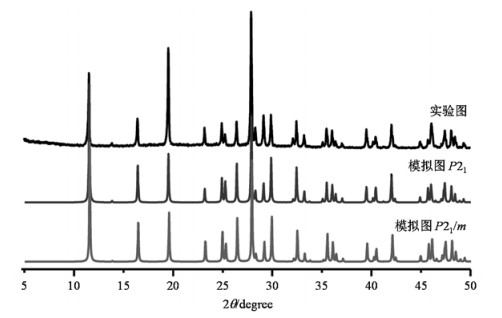
2 结果与讨论 2.1 层状La(OH)2NO3的结构和粉末XRD分析图 3描述了层状La(OH)2NO3(P21)的结构,在此化合物中,La3+为九配位,其中6个配位点来自于氢氧根中的氧原子(μ3-O),而剩余3个配位点来自于两个硝酸根中的氧原子[9].每个LaO9配位多面体通过μ3-O与6个LaO9配位多面体相连,沿b轴方向形成曲折的层状结构.硝酸根指向层状结构的空隙,每个硝酸根连接两个LaO9配位多面体.因此该化合物的最简配比为La:OH:NO3 = 1:2:1.值得一提的是,在早期的文献[10, 11]中,硝酸根离子的位置没有得到很好的解析,使得结构中存在一个通过La3+的对称镜面,导致晶体对称性升为P21/m并产生对称中心.图 4中的粉末XRD图谱展示了本文合成的层状La(OH)2NO3化合物样品的结晶性和相纯度,通过比较实验图谱和分别基于P21或P21/m结构的模拟图谱,发现产物为纯净的层状La(OH)2NO3化合物,而P21或P21/m结构上的差别在粉末XRD图谱上几乎不可分辨.
|
图 3 层状La(OH)2NO3(P21)的晶体结构和La3+的配位方式 Fig. 3 The crystal structure of layered La(OH)2NO3 (P21) and the coordination sphere of La3+ |
|
图 4 层状La(OH)2NO3的实验粉末XRD图谱(上)和分别基于P21(中)或P21/m(下)结构获得的模拟粉末XRD图谱 Fig. 4 A comparison between the experimental powder XRD pattern (top) of layered La(OH)2NO3 and the simulated powder XRD patterns based on P21 (middle) and P21/m (bottom) structures, respectively |
如前文所述,获取139La SSNMR谱图的难点在于,由于受到四极相互作用的强烈影响,139La NMR谱图往往具有非常大的宽度,导致了谱图信噪比较低.而且此时谱图宽度超出了常规探头中射频脉冲的激发宽度,在某一特定载波频率下获取的谱图线型只是整体线型的一部分,使用变频谱图采集方法获取的一系列频率步进分片NMR谱经过叠加后才能得到较为精确的整体线型[24].本文采用的QCPMG脉冲序列可以大幅度提升谱图信噪比,如图 5(a)所示,1 024次扫描(实验时间约8.5 min)后采集到的“类旋转边带”谱图就具有相当可观的信噪比,在使用图 2(b)所示的滤波方程处理之后,信噪比得到了显著提升[图 5(b)][22, 23].图 5(c)展示了经过滤波方程处理和谱图重建之后得到的与常规回波实验类似的谱图,其具有很高的信噪比并且保存了所有的谱图特征[22].本文描述的谱图采集、处理和重建方法可以用于获取各种四极核的高质量超宽SSNMR谱图.

|
图 5 (a) 当偏移量为0 kHz时,层状La(OH)2NO3的139La静态QCPMG“类旋转边带”谱图;(b) (a)图经过图 2(b)中滤波方程处理之后的图;(c) (b)图经过重建之后获得的谱图 Fig. 5 (a) The "spikelet" static 139La QCPMG spectrum of layered La(OH)2NO3 with an offset of 0 kHz; (b) The spectrum of Fig. (a) after processing with the filter function shown in Fig. 2(b); (c) The spectrum of Fig. (b) after spectral reconstruction |
在获取一系列高信噪比变频139La静态SSNMR谱图[如图 6(a)]之后,将它们进行叠加就可以得到整张超宽图谱[如图 6(b)].由此可见,整张谱图的线型和单片谱图有非常显著的差别.整张谱图包括窄而强的300 ~ −700 kHz的中心跃迁,以及宽而弱的3 500 ~ − 3 500 kHz的卫星跃迁(−3/2~3/2).值得注意的是,在本文使用的谱图采集、处理和重建条件下,完整的超宽−3/2~3/2卫星跃迁线型也被观测到,这在139La SSNMR谱图中尚未见文献报道.虽然卫星跃迁线型在SSNMR实验中很少被研究,但通过模拟卫星跃迁得到的四极相互作用参数比从中心跃迁中得到的更加精确,除此之外,卫星跃迁对于观测原子核周围微环境有序程度以及动态过程非常敏感,从中可以得到重要的结构信息[28-30].由于本文实验所用的外磁场场强较低(9.4 T),139La四极相互作用相比塞曼效应而言并不能被忽略,因此通常计算由四极相互作用产生的NMR谱线型时采用的高场假设并不能完全成立,尤其是对于卫星跃迁线型.常规NMR谱图模拟软件如WSolids、dmfit等在此情况下并不适用,本文使用了QUEST软件模拟同时包括中心跃迁和卫星跃迁的超宽NMR谱图[26].如图 6(c)所示,模拟图谱的特征与实验谱图匹配良好,−3/2~3/2卫星跃迁造成的谱图特征清晰可辩,相对应的NMR参数如下:各向同性化学位移为δiso(580±50),四极耦合常数CQ为(48.7±0.5)MHz,非对称因子ηQ为0.71,与九配位镧氧多面体的相关NMR参数正常范围相吻合[14].

|
图 6 (a) 当偏移量为0 kHz时,层状La(OH)2NO3的139La静态QCPMG重建谱图;(b)由一系列频率步进分片NMR谱图叠加得到的整张谱图;(c)使用QUEST软件获取的模拟谱图,只显示了中心跃迁和−3/2~3/2卫星跃迁的部分 Fig. 6 (a) The reconstructed static 139La QCPMG spectrum of layered La(OH)2NO3 with an offset of 0 kHz; (b) The co-added spectrum of a series of reconstructed static 139La QCPMG spectra with variable offsets; (c) The spectrum simulated using the QUEST software, with only the center transition and the −3/2~3/2 satellite transition being displayed for clarity |
近年来,使用Materials Studio中的CASTEP模块在周期性边界条件下进行密度泛函理论计算获得的NMR参数已被广泛用于NMR谱图解析,计算值和实验值往往有很好的吻合程度[31].本文分别采用CASTEP内置的“coarse”、“medium”或“fine”判据以及“Schroedinger”、“Koelling-Harmon”或“ZORA”相对论效应校正方法,对层状La(OH)2NO3化合物(P21结构)的139La NMR参数进行了计算,计算结果如表 1所示.值得一提的是,虽然四极耦合常数CQ实际上有正有负,但是在本文使用的实验条件下(以及在绝大多数情况下)只能测出其绝对值.因此,表 1中对四极耦合常数计算值进行了取绝对值操作.从计算结果与实验值的比较可以看出,不同相对论效应校正方法对139La NMR参数计算值造成的影响显著大于不同判据,其中采用“Koelling-Harmon”或“ZORA”相对论校正方法时,CASTEP理论计算结果与实验结果相当吻合.此时,即使采用相对“不精确”的“coarse”判据(即使用较低的能量收敛阈值)时也能得到较好的结果.此外,由于P21/m结构中存在未被完全占据的氮和氧位点[11],对其不能在周期性边界条件下直接进行计算,需要降低晶体对称性.在晶体学文件中添加羟基氢原子和降低对称性以消除未被完全占据的氮和氧位点之后,对所得晶体结构进行的计算表明,计算结果与实验结果的吻合程度明显低于基于P21结构的计算结果.
| 表 1 使用CASTEP模块计算得到的139La四极耦合常数(|CQ|)和非对称因子(ηQ) Table 1 The |CQ| and ηQ values of 139La calculated by CASTEP |
如2.1节所述,P21结构下层状La(OH)2NO3化合物具有一个九配位的镧位点,其镧氧键的距离在0.250~0.273 nm之间[9].与之不同,P21/m结构下层状La(OH)2NO3化合物具有一个十配位的镧位点,但是其中两个属于硝酸根的氧只有一半的占据几率,所以平均之后的镧配位数也为9,对应的镧氧键距离在0.224 ~ 0.280 nm之间[11].比较之后可知,P21/m结构下镧氧多面体的扭曲程度(由镧氧键的分布范围所决定)远远大于P21结构,与实验观测结果不符.139La SSNMR实验结果结合理论计算可以证实层状La(OH)2NO3化合物属于非中心对称的P21结构,因此展现出非线性光学特性[9].
3 结论本文描述了通过使用QCPMG脉冲序列、变频谱图采集、特定滤波方程处理、谱图重建和叠加获取高质量超宽静态139La SSNMR谱图的方法,并成功获取了宽度接近7 MHz、同时包含中心跃迁和−3/2~3/2卫星跃迁的层状La(OH)2NO3化合物的谱图.所获谱图可以通过使用QUEST软件进行模拟,得到的实验NMR参数与基于P21结构的在周期性边界条件下进行的密度泛函理论计算结果吻合,从而确认了本文中合成的层状La(OH)2NO3化合物属于非中心对称的P21结构.本文中使用的方法可广泛用于对各类四极核化合物进行SSNMR研究,并可结合密度泛函理论计算等获取化合物的重要结构信息.
| [1] | SELS B, VOS D D, BUNTINX M, et al. Layered double hydroxides exchanged with tungstate as biomimetic catalysts for mild oxidative bromination[J]. Nature, 1999, 400(6747): 855-857. DOI: 10.1038/23674. |
| [2] | LEROUX F, BESSE J P. Polymer interleaved layered double hydroxide: A new emerging class of nanocomposites[J]. Chem Mater, 2001, 13(10): 3507-3515. DOI: 10.1021/cm0110268. |
| [3] | KHAN A I, O'HARE D. Intercalation chemistry of layered double hydroxides:Recent developments and applications[J]. J Mater Chem, 2002, 12(11): 3191-3198. DOI: 10.1039/B204076J. |
| [4] | SELS B F, DE VOS D E, BUNTINX M, et al. Transition metal anion exchanged layered double hydroxides as a bioinspired model of vanadium bromoperoxidase[J]. J Catal, 2003, 216(1): 288-297. |
| [5] | LIANG J B, MA R Z, SASAKI T. Layered rare earth hydroxides (LREHs):Synthesis and structure characterization towards multifunctionality[J]. Dalton Trans, 2014, 43(27): 10355-10364. DOI: 10.1039/C4DT00425F. |
| [6] | ZHU Q, WANG X J, LI J G. Recent progress in layered rare-earth hydroxide (LRH) and its application in luminescence[J]. J Adv Ceram, 2017, 6(3): 177-186. DOI: 10.1007/s40145-017-0238-0. |
| [7] | XU J, CHEN X Y, XU Y S, et al. Ultrathin 2D rare-earth nanomaterials:Compositions, syntheses, and applications[J]. Adv Mater, 2019: e1806461. DOI: 10.1002/adma.201806461. |
| [8] | NEWMAN S P, JONES W. Comparative study of some layered hydroxide salts containing exchangeable interlayer anions[J]. J Solid State Chem, 1999, 148(1): 26-40. DOI: 10.1006/jssc.1999.8330. |
| [9] | SONG Y X, LUO M, LIN C S, et al. Structural modulation of nitrate group with cations to affect SHG responses in RE(OH)2NO3 (RE=La, Y, and Gd):New polar materials with large NLO effect after adjusting pH values of reaction systems[J]. Chem Mater, 2017, 29(2): 896-903. DOI: 10.1021/acs.chemmater.6b05119. |
| [10] | HASCHKE J M. Preparation, phase equilibriums, crystal chemistry, and some properties of lanthanide hydroxide nitrates[J]. Inorg Chem, 1974, 13(8): 1812-1818. DOI: 10.1021/ic50138a006. |
| [11] | LOUER M, LOUER D, LOPEZ DELGADO A, et al. The structures of lanthanum hydroxide nitrates investigated by the Rietveld profile refinement technique[J]. Eur J Solid State Inorg Chem, 1989, 20(50): 241-253. |
| [12] | ALBA M D, CHAIN P, FLORIAN P, et al. 45Sc spectroscopy of solids:Interpretation of quadrupole interaction parameters and chemical shifts[J]. J Phys Chem C, 2010, 114(28): 12125-12132. DOI: 10.1021/jp1036525. |
| [13] | BR UNIGER T, HOFMANN A J, MOUDRAKOVSKI I L, et al. A 45Sc-NMR and DFT calculation study of crystalline scandium compounds[J]. Solid State Sci, 2016: 511-7. |
| [14] | PATERSON A L, HANSON M A, WERNER-ZWANZIGER U, et al. Relating 139La quadrupolar coupling constants to polyhedral distortion in crystalline structures[J]. J Phys Chem C, 2015, 119(45): 25508-25517. DOI: 10.1021/acs.jpcc.5b09122. |
| [15] |
LI D B, XU S, YU Z W. Application of solid-state NMR to bone and bone biomaterials[J].
Chinese J Magn Reson, 2017, 34(1): 115-129.
李东北, 许帅, 喻志武. 固体核磁共振技术在骨基生物材料研究中的应用[J]. 波谱学杂志, 2017, 34(1): 115-129. |
| [16] | XU J, TERSKIKH V V, HUANG Y. Resolving multiple non-equivalent metal sites in magnesium-containing metal-organic frameworks by natural abundance 25Mg solid-state NMR spectroscopy[J]. Chem Eur J, 2013, 19(14): 4432-4436. DOI: 10.1002/chem.201300113. |
| [17] | XU J, TERSKIKH V V, CHU Y, et al. Mapping out chemically similar, crystallographically nonequivalent hydrogen sites in metal-organic frameworks by 1H solid-state NMR spectroscopy[J]. Chem Mater, 2015, 27(9): 3306-3316. DOI: 10.1021/acs.chemmater.5b00360. |
| [18] |
JIANG T T, FU X B, WU J Z, et al. Structure and dynamics of polymer-ceramic interface in Li1.5Al0.5Ge1.5P3O12/polyether solid electrolyte:A solid-state NMR study[J].
Chinese J Magn Reson, 2017, 34(4): 429-438.
姜婷婷, 付晓彬, 吴金泽, 等. Li1.5Al0.5Ge1.5P3O12高分子固体电解质表界面结构与分子运动的固体NMR研究[J]. 波谱学杂志, 2017, 34(4): 429-438. |
| [19] | HARRIS R K, BECKER E D, CABRAL DE MENEZES S M, et al. NMR nomenclature. Nuclear spin properties and conventions for chemical shifts (IUPAC recommendations 2001)[J]. Pure Appl Chem, 2001, 73(11): 1795-1818. DOI: 10.1351/pac200173111795. |
| [20] | PYYKK P. Year-2017 nuclear quadrupole moments[J]. Mol Phys, 2018, 116(10): 1328-1338. DOI: 10.1080/00268976.2018.1426131. |
| [21] | LARSEN F H, JAKOBSEN H J, ELLIS P D, et al. Sensitivity-enhanced quadrupolar-echo NMR of half-integer quadrupolar nuclei. Magnitudes and relative orientation of chemical shielding and quadrupolar coupling tensors[J]. J Phys Chem A, 1997, 101(46): 8597-8606. DOI: 10.1021/jp971547b. |
| [22] | LEFORT R, WIENCH J W, PRUSKI M, et al. Optimization of data acquisition and processing in Carr-Purcell-Meiboom-Gill multiple quantum magic angle spinning nuclear magnetic resonance[J]. J Chem Phys, 2002, 116(6): 2493-2501. DOI: 10.1063/1.1433000. |
| [23] | HUNG I, GAN Z H. On the practical aspects of recording wideline QCPMG NMR spectra[J]. J Magn Reson, 2010, 204(2): 256-265. DOI: 10.1016/j.jmr.2010.03.001. |
| [24] | MASSIOT D, FARNAN I, GAUTIER N, et al. 71Ga and 69Ga nuclear magnetic resonance study of β-Ga2O3:Resolution of four-and six-fold coordinated Ga sites in static conditions[J]. Solid State Nucl Magn Reson, 1995, 4(4): 241-248. DOI: 10.1016/0926-2040(95)00002-8. |
| [25] | BENNETT A E, RIENSTRA C M, AUGER M, et al. Heteronuclear decoupling in rotating solids[J]. J Chem Phys, 1995, 103(16): 6951-6958. DOI: 10.1063/1.470372. |
| [26] | PERRAS F A, WIDDIFIELD C M, BRYCE D L. QUEST-QUadrupolar Exact SofTware:A fast graphical program for the exact simulation of NMR and NQR spectra for quadrupolar nuclei[J]. Solid State Nucl Magn Reson, 2012: 45-4636-44. |
| [27] | CLARK S J, SEGALL M D, PICKARD C J, et al. First principles methods using CASTEP[J]. Z Kristallogr, 2005, 220(5-6): 567-570. |
| [28] | GROSZEWICZ P B, BREITZKE H, DITTMER R, et al. Nanoscale phase quantification in Lead-free (Bi1/2Na1/2)TiO3-BaTiO3 relaxor ferroelectrics by means of 23Na NMR[J]. Phys Rev B, 2014, 90(22): 220104. DOI: 10.1103/PhysRevB.90.220104. |
| [29] | DI BITETTO A, ANDR E, CARTERET C, et al. Probing the dynamics of layered double hydroxides by solid-state 27Al NMR spectroscopy[J]. J Phys Chem C, 2017, 121(13): 7276-7281. DOI: 10.1021/acs.jpcc.6b13106. |
| [30] | DAWSON D M, GRIFFIN J M, SEYMOUR V R, et al. A multinuclear NMR study of six forms of AlPO-34:Structure and motional broadening[J]. J Phys Chem C, 2017, 121(3): 1781-1793. DOI: 10.1021/acs.jpcc.6b11908. |
| [31] | BONHOMME C, GERVAIS C, BABONNEAU F, et al. First-principles calculation of NMR parameters using the Gauge Including Projector Augmented Wave Method:A chemist's point of view[J]. Chem Rev, 2012, 112(11): 5733-5779. DOI: 10.1021/cr300108a. |
 2020, Vol. 37
2020, Vol. 37 
