2. 中国科学院大学, 北京 100049;
3. 油气资源与探测国家重点实验室, 中国石油大学(北京), 北京 102249
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China
磁共振成像(MRI)因具备无损伤、无电离辐射、成像参数多等优点,而成为重要的科学研究和临床诊断手段[1-5].由于质子(1H)的核磁共振(NMR)信号较强,常规MRI都是基于质子,即对生物体内的水质子进行成像,而基于质子的MRI包含的代谢、离子交换等生物学信息较少.23Na、31P、17O等非质子核也可以提供丰富的生物学信息[6, 7],因此基于杂核(X核)的成像在医学及生命科学研究中愈来愈重要.31P作为生物体内的重要元素,几乎参与所有生物学过程[8],这使31P MRI成为X核成像中的热点研究领域.但31P MRI的信噪比(SNR)和分辨率较低,需要借助质子成像实现关注区域的定位和匀场[9],而且基于两种原子获得的磁共振图像需要相互印证分析.而传统MRI系统仅支持单核成像,要获得1H图像和31P图像,需进行两次扫描.这不仅会增加成像时间,而且可能因两次扫描过程中被测对象的移动导致1H图像和31P图像难以配准.使用1H/31P双核并行成像技术,单次扫描即可同时获得1H图像和31P图像,既缩短双核成像时间,也保证了1H图像和31P图像间的配准,有重大的实用价值.然而目前国内还没有成熟的多核并行MRI系统,因此自主研发多核并行MRI系统有重大的科研意义及商用价值.
射频线圈是MRI系统的关键部件之一,线圈是否具备多核并行成像能力直接关系到MRI系统能否实现多核并行成像.本文针对1H/31P并行成像的研究需求,提出了一种1H/31P双核并行成像线圈的设计方案.根据现有Bruker 4.7 T磁体的孔径,建立了一套双核并行成像线圈模型,并用HFSS仿真软件(Ansoft公司)对线圈的结构及参数进行了仿真设计.该线圈包括相互独立的1H通道和31P通道,1H线圈和31P线圈均采用收发分离式结构.1H线圈用低通鸟笼线圈做发射线圈,马鞍线圈做接收线圈;31P线圈用高通鸟笼线圈做发射线圈,双阵列线圈做接收线圈.对阵列线圈的耦合及去耦进行了理论分析,提出了利用LC并联trap进行去耦的方法,该方法具有较强的环境适应性,可在保证去耦效果的同时简化线圈调试过程.结合仿真结果制作了1H/31P双核并行成像线圈,对线圈进行了电性能测试,并将研制的双核并行成像线圈应用于Bruker 4.7 T磁体系统,利用自主研发的多核并行MRI系统开展MRI并行成像实验测试,验证了本文提出的双核并行成像线圈设计方案的可行性,为双核乃至多核并行成像线圈的进一步研究积累了经验.
1 1H/31P双核并行成像线圈设计由于31P NMR信号较弱,线圈需针对31P核进行优化以提高信噪比.让线圈贴近被测物体可提高线圈的灵敏度,从而提高信噪比.但对于收发一体式线圈,其发射场(B1+)与接收场(B1-)的分布是一致的,线圈靠近被测样品时,其射频场均匀性会降低,导致线圈性能下降.而收发分离式线圈用一个线圈做发射,另一个线圈做接收,其B1+与B1-不一致,可以在保证发射射频场均匀性的同时,保证接收灵敏度的最大化[10].若31P线圈采用收发分离式结构而1H线圈采用收发一体式结构,受31P发射线圈的影响,线圈由发射阶段(31P发射线圈处于工作状态)进入接收阶段(31P发射线圈处于失谐状态)时,1H线圈的谐振频率会漂移,使线圈无法进行并行成像.为避免该问题,本文的双核并行成像线圈的1H线圈和31P线圈均采用收发分离式结构.
1.1 发射线圈鸟笼线圈能在大尺寸范围内产生高均匀度的射频场[11],是最常见的一种成像体线圈,本文使用鸟笼线圈作为发射线圈.
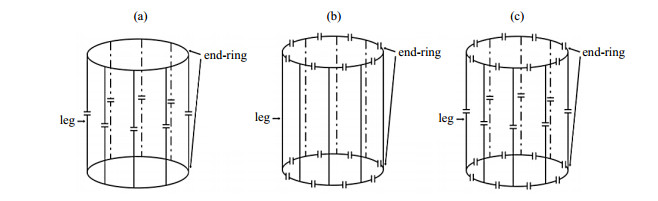
1.1.1 鸟笼线圈原理鸟笼线圈由leg及end-ring构成,leg为柱面上平行于轴线且等间距分布的导体,end-ring为连接各个leg以构成回路的导体.鸟笼线圈上分布有电容,用于构成谐振回路,根据电容位置的不同,鸟笼线圈可分为低通鸟笼线圈、高通鸟笼线圈、带通鸟笼线圈,其结构如图 1所示.
|
图 1 鸟笼线圈模型.(a)低通鸟笼线圈;(b)高通鸟笼线圈;(c)带通鸟笼线圈 Fig. 1 Model of birdcage coil. (a) Low-pass birdcage coil; (b) High-pass birdcage coil; (c) Band-pass birdcage coil |
不同类型鸟笼线圈有着不同的谐振模式,若鸟笼线圈leg的电感为M,连接相邻leg的导体所对应的电感为L,leg或end-ring上的电容为C(对于带通鸟笼,leg上的电容取为
低通鸟笼线圈:
| ${\omega _m} = {\left\{ {C[M + L/(2{{\sin }^2}\frac{{{\rm{ \mathsf{ π} }}m}}{N})]} \right\}^{ - 1/2}}{\rm{ }}m = 0, 1, 2, \cdots , \frac{N}{2}$ | (1) |
高通鸟笼线圈:
| ${\omega _m} = {\left[ {C(L + 2M{{\sin }^2}\frac{{{\rm{ \mathsf{ π} }}m}}{N})} \right]^{ - 1/2}}{\rm{ }}m = 0, 1, 2, \cdots , \frac{N}{2}$ | (2) |
带通鸟笼线圈:
| ${\omega _m} = {\left[ {(L + 2M{{\sin }^2}\frac{{{\rm{ \mathsf{ π} }}m}}{N})/(\frac{2}{{{C_1}}}{{\sin }^2}\frac{{{\rm{ \mathsf{ π} }}m}}{N} + \frac{1}{{{C_2}}})} \right]^{ - 1/2}}{\rm{ }}m = 0, 1, 2, \cdots , \frac{N}{2}$ | (3) |
m为谐振模式的模式变量:m=0时,leg上无电流,end-ring上有电流,该模式被称为end-ring模式;m=1时,leg上电流满足正弦电流分布,该模式能在线圈内产生均匀的射频场.低通鸟笼线圈m=0模式的谐振频率为0,m=1模式的谐振频率为非0的最低频率;高通鸟笼线圈m=0模式的谐振频率最高,m=1模式的谐振频率为第二高的频率;带通鸟笼线圈m=0及m=1模式的谐振频率则不一定为最高或最低,与
考虑到两个核的线圈的独立性,使用两个鸟笼线圈实现双频共振.由于低通鸟笼线圈m > 1模式的谐振频率都比m=1模式的谐振频率高,而高通鸟笼线圈m > 1模式的谐振频率都比m=1模式的谐振频率低,为了减小两个线圈间的耦合,采用低通鸟笼线圈作为1H发射线圈,高通鸟笼线圈作为31P发射线圈.为了进一步减小两个鸟笼线圈间的耦合,将两个鸟笼线圈的legs相互交错,同时两个鸟笼线圈的end-ring也错开一定距离.因为低通鸟笼线圈馈电点与轴线所构成的平面(以下称作馈电平面)与其射频场的方向垂直,而高通鸟笼线圈馈电平面与其射频场方向平行.具体如图 2(a)和2(b)所示,若高通鸟笼线圈及低通鸟笼线圈的馈电点均位于XZ平面,则高通鸟笼线圈的射频场方向与X轴平行,而低通鸟笼线圈的射频场方向与Y轴平行.所以将两个鸟笼线圈的馈电平面重合,使两个鸟笼线圈间的射频场方向相互垂直,确保两个鸟笼线圈间的耦合最小化.

|
图 2 (a) 低通鸟笼线圈射频场方向;(b)高通鸟笼线圈射频场方向;(c)双核鸟笼线圈仿真模型 Fig. 2 (a) RF field direction of low-pass birdcage coil; (b) RF field direction of high-pass birdcage coil; (c) Simulation model of dual-nuclear birdcage coil |
线圈导体及屏蔽层用铜箔制作,综合空间尺寸约束、射频场均匀度等因素,将两个鸟笼线圈leg数(N)定为8.两个鸟笼线圈的leg均用厚度为0.1 mm、宽度为5 mm的铜箔制作,end-ring用厚度为0.1 mm、宽度为10 mm的铜箔制作,电容间隙为1.5 mm;1H低通鸟笼线圈半径为46.5 mm,leg长为100 mm;31P高通鸟笼线圈半径为34.5 mm,leg长为140 mm;屏蔽层半径为55 mm.根据以上参数,对线圈进行仿真分析以获取适合的电容值.仿真所用线圈模型如图 2(c)所示,模型中低通鸟笼线圈leg上串有两个电容,而非理论模型上只有一个电容,这样可以在保证线圈对称性的同时方便对线圈进行馈电.
对线圈上电容的值进行仿真优化后,结果如图 3所示,可知当低通鸟笼线圈leg上的电容为13.2 pF时,线圈m=1模式的谐振频率为200 MHz(对应4.7 T场强下1H核的Larmor频率);高通鸟笼线圈end-ring上的电容为95 pF时,线圈m=1模式的谐振频率为81 MHz(对应4.7 T场强下31P的Larmor频率).从线圈的S21参数(表示能量传递系数,用来表征隔离度)可看出1H线圈和31P线圈间的耦合低于-30 dB,可满足双核同步成像实验的需求.

|
图 3 双核鸟笼线圈S参数仿真结果. (a) S11、S22;(b) S21 Fig. 3 S-parameter simulation results of double-nuclear birdcage coil. (a) S11, S22; (b) S21 |
由于发射线圈与接收线圈的谐振频率相同,如果两种线圈同时处于工作状态,则发射线圈和接收线圈间会有很强的耦合,使得线圈性能下降,甚至会损坏前置放大器及功率放大器.为了避免这种情况,需要在线圈上设计失谐电路,以保证发射线圈和接收线圈不会同时处于工作状态.
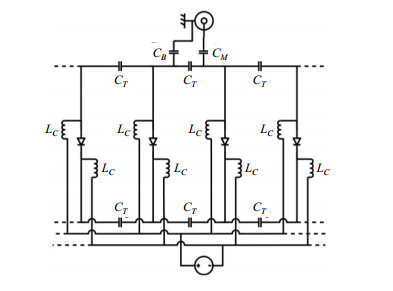
当鸟笼线圈的legs都断开时,电流无法流过leg,除end-ring模式外,其余模式均消失,这时鸟笼线圈处于失谐状态[13].基于这种现象,在鸟笼线圈的每个leg上串一个PIN二极管,用直流偏置控制PIN二极管的导通与截止,当PIN二极管导通时鸟笼线圈处于工作状态,当PIN二极管截止时,鸟笼线圈处于失谐状态.为了避免射频信号进入直流驱动电路、直流电流进入功率放大器,在直流偏置电路上加上扼流电感,同时鸟笼线圈的馈电链路上也加上隔直电容.图 4为鸟笼线圈主动失谐电路原理图.
|
图 4 鸟笼线圈主动失谐原理图 Fig. 4 Principle diagram of active detuning for birdcage coil |
由于31P NMR信号较弱,为了进一步提高31P NMR的信噪比,31P核采用双阵列线圈进行接收并安装于最内层,而1H NMR信号较强,因此采用马鞍形线圈进行接收.
1.2.1 接收线圈结构设计与仿真31P接收线圈为双阵列线圈,线圈单元的形状为鞍形,两个线圈单元在圆筒上相对放置;1H接收线圈为马鞍形线圈.对线圈的射频场分布进行仿真,其仿真模型如图 5(b)所示,双核接收线圈在空间上相互正交,从而保证其射频场方向的相互正交,以提高双核接收线圈间的隔离度.线圈用厚0.1 mm、宽5 mm的铜箔制作,1H马鞍线圈的半径为22 mm、高度为60 mm,31P阵列线圈的半径为16 mm、高度为40 mm.对鞍形结构的张角θ[图 5(a)]进行优化,使马鞍线圈及阵列线圈能产生较为均匀的射频场.仿真结果显示当θ=120˚时,马鞍线圈及双阵列线圈产生的射频场较为均匀.

|
图 5 (a) 鞍形线圈张角(θ);(b)接收线圈仿真模型;(c) 1H马鞍线圈射频场分布;(d) 31P双阵列线圈射频场分布 Fig. 5 (a) Arc angle (θ) of saddle coil; (b) Receiving coil simulation model; (c) RF field distribution of 1H saddle coil; (d) RF field distribution of 31P double array coil |
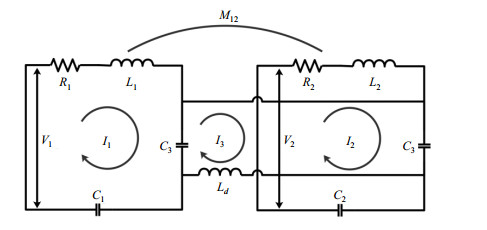
由于双阵列线圈的线圈单元间有耦合,而线圈间的耦合会导致线圈谐振频率裂分,降低线圈接收效率,所以阵列线圈的去耦至关重要.常用双阵列线圈去耦方法有:重叠面积去耦[14, 15]、低输入阻抗前置放大器去耦[15]、电路网络去耦[16-19].重叠面积去耦法限定了线圈单元的位置,不便于对线圈的射频场进行优化,同时该方法也不便于实际调试.低输入阻抗前置放大器去耦法需要特殊的前放,且对强耦合的去耦效果不佳.电路网络去耦法,如电容去耦、电感去耦,去耦效果不依赖于线圈单元的位置,可方便对双阵列线圈的射频场进行优化.本文在电感去耦法的基础上加以改进,使用LC并联trap进行双阵列线圈去耦.电感去耦法的原理图如图 6所示,图中用RLC串联电路代表单个线圈.用基尔霍夫定律对线圈进行分析:
| ${V_1} = ({R_1} + {\rm{j}}\omega {L_1} + \frac{1}{{{\rm{j}}\omega {C_1}}} + \frac{1}{{{\rm{j}}\omega {C_3}}}){I_1} - ({\rm{j}}\omega {M_{12}}{I_2} + \frac{1}{{{\rm{j}}\omega {C_3}}}{I_3})$ | (4) |
| ${V_2} = ({R_2} + {\rm{j}}\omega {L_2} + \frac{1}{{{\rm{j}}\omega {C_2}}} + \frac{1}{{{\rm{j}}\omega {C_3}}}){I_2} - ({\rm{j}}\omega {M_{12}}{I_1} - \frac{1}{{{\rm{j}}\omega {C_3}}}{I_3})$ | (5) |
| $({\rm{j}}\omega {L_d} + \frac{2}{{{\rm{j}}\omega {C_3}}}){I_3} - \frac{1}{{{\rm{j}}\omega {C_3}}}{I_1} + \frac{1}{{{\rm{j}}\omega {C_3}}}{I_2} = 0$ | (6) |
|
图 6 电感去耦原理图 Fig. 6 Principle diagram of inductive decoupling |
其中,V表示电压;ω为角频率,ω= 2πf.由(6)式可得:
| ${I_3} = \frac{1}{{2 - {\omega ^2}{L_d}{C_3}}}({I_2} - {I_1})$ | (7) |
将(7)式代入(4)、(5)式可得:
| ${V_1} = \left[ {{R_1} + {\rm{j}}\omega {L_1} + \frac{1}{{{\rm{j}}\omega {C_1}}} + \frac{1}{{{\rm{j}}\omega {C_3}}} + \frac{1}{{{\rm{j}}\omega {C_3}(2 - {\omega ^2}{L_d}{C_3})}}} \right]{I_1} - \left[ {{\rm{j}}\omega {M_{12}} + \frac{1}{{{\rm{j}}\omega {C_3}(2 - {\omega ^2}{L_d}{C_3})}}} \right]{I_2}$ | (8) |
| ${V_2} = \left[ {{R_2} + {\rm{j}}\omega {L_2} + \frac{1}{{{\rm{j}}\omega {C_2}}} + \frac{1}{{{\rm{j}}\omega {C_3}}} + \frac{1}{{{\rm{j}}\omega {C_3}(2 - {\omega ^2}{L_d}{C_3})}}} \right]{I_2} - \left[ {{\rm{j}}\omega {M_{12}} + \frac{1}{{{\rm{j}}\omega {C_3}(2 - {\omega ^2}{L_d}{C_3})}}} \right]{I_1}$ | (9) |
要使线圈间的耦合最小,则需消除耦合项
| ${\rm{j}}\omega {M_{12}} + \frac{1}{{{\rm{j}}\omega {C_3}(2 - {\omega ^2}{L_d}{C_3})}} = 0$ | (10) |
则:
| ${L_d} = \frac{{2{\omega ^2}{M_{12}}{C_3} - 1}}{{{\omega ^4}{M_{12}}C_3^2}}$ | (11) |
本文设计的双阵列线圈间的互感
LC并联trap的导纳为:
| $Y = {\rm{j}}(\omega C - \frac{1}{{\omega L}}) = - {\rm{j}}\frac{1}{{\omega L'}}$ | (12) |
| $L' = \frac{L}{{1 - {{(\frac{\omega }{{{\omega _0}}})}^2}}}, {\rm{ }}{\omega _0} = \frac{1}{{\sqrt {{\rm{LC}}} }}$ | (13) |
由(13)式可知,当工作频率
为保证发射线圈与接收线圈分时工作,除需在发射线圈上加失谐电路外,接收线圈也需加上失谐电路.本文使用被动失谐的方式对接收线圈进行失谐,将反向并联的二极管对与一个电感串联后并联在接收线圈通路的电容上.发射阶段,发射线圈发射的高功率射频脉冲会使接收线圈中的二极管对导通,电容与电感并联后在其谐振频率处形成高阻态,使接收线圈失谐;接收阶段,NMR信号无法使二极管导通,接收线圈处于正常工作状态.
2 1H/31P双核并行成像线圈制作线圈整体结构由五层圆筒构成,圆筒的材料为聚甲醛(polyoxymethylene,POM),表 1为每层圆筒的尺寸及功能.其中用于承载鸟笼线圈的两个圆筒上刻有鸟笼形状的凹槽,凹槽深度为0.5 mm.位于最外层的屏蔽层由两层铜箔构成,两层铜箔沿POM管轴向的缝隙分为若干部分,内外两层铜箔的缝隙相互交错,使两层铜箔构成一个整体的屏蔽层,同时可有效减小涡流的影响.线圈及屏蔽层实物图如图 7所示.
| 表 1 圆筒尺寸及功能 Table 1 The sizes and functions of the cylinders |

|
图 7 线圈实物图.(a) 1H低通鸟笼线圈;(b) 31P高通鸟笼线圈;(c) 1H马鞍接收线圈;(d) 31P双阵列接收线圈;(e)屏蔽层;(f)装配后的线圈 Fig. 7 Pictures of the coils. (a) 1H low-pass birdcage coil; (b) 31P high-pass birdcage coil; (c) 1H saddle receiving coil; (d) 31P double array receiving coil; (e) RF shield; (f) Assembled coil |
线圈所用定值电容为DLI公司的C17AH系列无磁电容,可调电容为Voltronics公司的无磁可调电容.鸟笼线圈主动失谐所用的PIN二极管为MACOM公司的MA4P7102F-1072T无磁高功率PIN管,扼流电感则为手工绕制的电感,感值分别为1.6 μH(由于寄生电容的影响,其S21参数在81 MHz时小于-20 dB)及0.68 μH(由于寄生电容的影响,其S21参数在200 MHz时小于-20 dB).驱动电路偏置电压为5 V(反压-15 V),通过功率电阻后给PIN二极管提供100 mA的正偏电流.接收线圈被动失谐所用开关二极管为Toshiba公司的BAS316,H3F二极管.
3 1H/31P双核并行成像线圈测试 3.1 电性能测试用ROHDE & SCHWARZ公司的ZNB20矢量网络分析仪对线圈进行测试.图 8(a)为双核鸟笼线圈测试结果,可见两个鸟笼线圈能分别工作于200 MHz及81 MHz,且两个线圈间的耦合较小,低于-25 dB.图 8(b)为31P双阵列线圈测试结果,可见在加入LC trap去耦后,两个线圈的谐振峰均无裂分,且在81 MHz时线圈间的耦合低于-20 dB,说明该方法有效地消除了双阵列线圈间的耦合.

|
图 8 (a) 双核鸟笼线圈S参数;(b) 31P双阵列接收线圈S参数 Fig. 8 (a) S-parameter of dual-nuclear birdcage coil; (b) S-parameter of 31P double array receiving coil |
在Bruker 4.7 T磁体上,利用自主研发的多核并行MRI系统和本文设计的1H/31P双核并行成像线圈进行联机测试:样品为85%的浓磷酸溶液,采用双核GRE并行序列同步采集1H核和31P核的信号.成像参数为:扫描次数(NS)=1,重复时间(TR)=2 000 ms,回波时间(TE)=5 ms,成像视野(FOV)=100 mm×100 mm,层厚(slice thickness)=10 mm,矩阵(matrix size)=256×256.样品实物及成像结果如图 9所示,实验取得了对比清晰且较为均匀的图像,验证了该双核并行成像线圈的可用性;测试过程和成像结果均表明1H和31P的发射线圈及接收线圈能正常地分时工作,验证了主动失谐及被动失谐方案的可行性;同时,从31P图像可看出阵列线圈的两个线圈单元能独立地进行成像,两个线圈图像间的干扰较小,且加权重建后的图像均匀性较好,验证了所用LC trap去耦方案的可行性.

|
图 9 样品实物及并行成像结果.(a)85%浓磷酸样品;(b) 1H磁共振图像;(c)加权重建31P磁共振图像 Fig. 9 Picture of the sample and images of the parallel imaging. (a) 85% H3PO4 sample; (b) 1H MR image; (c) Weighted reconstructed 31P MR image |
本文对鸟笼线圈工作原理及工作模式进行了深入分析,提出一种用双鸟笼线圈实现1H/31P双核共振的方案,并对双核鸟笼线圈进行了仿真,结果表明该方案在实现双核共振的同时能保证通道间的高隔离度;对马鞍线圈、双鞍形阵列线圈进行了仿真,表明设计的马鞍线圈、双鞍形阵列线圈能产生均匀度较好的射频场.用矢量网络分析仪对线圈的性能进行了测试,双核鸟笼线圈的隔离度可达25 dB以上,双阵列接收线圈的隔离度可达20 dB以上;进行了双核并行MRI实验,成功获得了1H核和31P核的并行磁共振图像,验证了该并行成像线圈设计方案及LC并联trap去耦方法的可行性,为双核乃至多核并行成像线圈的进一步研究奠定了基础.
| [1] |
XIE H B, LI J Q, YANG G. The data sampling system of medical MRI base on NMR spectrometer[J].
Chinese J Magn Reson, 2004, 21(4): 475-483.
谢海滨, 李建奇, 杨光. 医学MRI系统的FSE实现[J]. 波谱学杂志, 2004, 21(4): 475-483. DOI: 10.3969/j.issn.1000-4556.2004.04.011. |
| [2] |
MEI L X, WANG H, LI G Y. A two-channel surface coil for vertebral imaging on low-field MRI systems[J].
Chinese J Magn Reson, 2008, 25(1): 33-38.
梅立雪, 王鹤, 李鲠颖. 低场MRI系统中2通道脊椎线圈的研制[J]. 波谱学杂志, 2008, 25(1): 33-38. DOI: 10.3969/j.issn.1000-4556.2008.01.005. |
| [3] |
XIAO P F, SHEN J, JIANG Y, et al. Bench-top magnetic resonance imaging system[J].
Chinese J Magn Reson, 2002, 19(4): 345-352.
肖鹏飞, 沈杰, 蒋赟, 等. 台式磁共振成像系统的研制[J]. 波谱学杂志, 2002, 19(4): 345-352. DOI: 10.3969/j.issn.1000-4556.2002.04.002. |
| [4] |
HUANG C H, ZHANG Z, CHEN L, et al. A time-division multiplexing design for gradient preemphasis module in magnetic resonance imaging scanner[J].
Chinese J Magn Reson, 2018, 35(4): 68-77.
黄朝晖, 张志, 陈黎, 等. MRI梯度预加重模块的分时复用设计[J]. 波谱学杂志, 2018, 35(4): 68-77. |
| [5] |
LU S, CHANG Y, QIAN S S, et al. Optimization of selective radio frequency pulses for simultaneous multi-slice MRI[J].
Chinese J Magn Reson, 2018, 35(2): 141-149.
卢杉, 常严, 钱嵩松, 等. 用于同时多层MRI的选择性射频脉冲的优化设计[J]. 波谱学杂志, 2018, 35(2): 141-149. |
| [6] | KAGGIE J D, SAPKOTA N, THAPA B, et al. Synchronous radial 1H and 23Na dual-nuclear MRI on a clinical MRI system, equipped with a broadband transmit channel[J]. Concept Magn Reson B, 2016, 46(4): 191-201. |
| [7] | WILCOX M D, DEL B R, PARIZEK K, et al. A three-element 1H-31P dual-tuned array for magnetic resonance spectroscopy at 4.7 T[J]. Conf Proc IEEE Eng Med Biol Soc, 2016: 6258-6261. |
| [8] | DU F, LIU S P, CHEN Q Y, et al. Numerical simulation and evaluation of a four-channel-by-four-channel double-nuclear RF coil for 1H MRI and 31P MRSI at 7 T[J]. IEEE T Magn, 2018, 54(11): 5101105. |
| [9] | HONG S M, CHOI C H, MAGILL A W, et al. Design of a quadrature 1H/31P coil using bent dipole antenna and 4-channel loop at 3T MRI[J]. IEEE T Med Imaging, 2018, 37(12): 2613-2618. DOI: 10.1109/TMI.2018.2844462. |
| [10] | DOGANAY O, THIND K, WADE T, et al. Transmit-only/receive-only radiofrequency coil configuration for hyperpolarized 129Xe MRI of rat lungs[J]. Concept Magn Reson B, 2015, 45(3): 115-124. DOI: 10.1002/cmr.b.21288. |
| [11] | HAYES C E, EDELSTEIN W A, SCHENCK J F, et al. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T[J]. J Magn Reson, 1985, 63(3): 622-628. |
| [12] | JIN J M. Electromagnetic analysis and design in magnetic resonance imaging[M]. Boca Raton, FL: CRC Press, 1999. |
| [13] | BARBERI E A, GATI J S, RUTT B K, et al. A transmit-only/receive-only (TORO) RF system for high-field MRI/MRS applications[J]. Magn Reson Med, 2000, 43(2): 284-289. DOI: 10.1002/(SICI)1522-2594(200002)43:2<284::AID-MRM16>3.0.CO;2-C. |
| [14] | AVDIEVICH N I, GIAPITZAKIS I A, PFROMMER A, et al. Decoupling of a tight-fit transceiver phased array for human brain imaging at 9.4T:Loop overlapping rediscovered[J]. Magn Reson Med, 2018, 79(2): 1200-1211. DOI: 10.1002/mrm.26754. |
| [15] | ROEMER P B, EDELSTEIN W A, HAYES C E, et al. The NMR phased array[J]. Magn Reson Med, 1990, 16(2): 192-225. DOI: 10.1002/mrm.1910160203. |
| [16] | WU B, ZHANG X L, QU P, et al. Design of an inductively decoupled microstrip array at 9.4 T[J]. J Magn Reson, 2006, 182(1): 126-132. DOI: 10.1016/j.jmr.2006.04.013. |
| [17] | LEE R F, GIAQUINTO R O, HARDY C J. Coupling and decoupling theory and its application to the MRI phased array[J]. Magn Reson Med, 2002, 48(1): 203-213. DOI: 10.1002/mrm.10186. |
| [18] | MOGATADAKALA K V, BANKSON J A, NARAYANA P A. Three-element phased-array coil for imaging of rat spinal cord at 7 T[J]. Magn Reson Med, 2008, 60(6): 1498-1505. DOI: 10.1002/mrm.21777. |
| [19] | ZHANG X R, WEBB A. Design of a capacitively decoupled transmit/receive NMR phased array for high field microscopy at 14.1 T[J]. J Magn Reson, 2004, 170(1): 149-155. DOI: 10.1016/j.jmr.2004.05.004. |
 2020, Vol. 37
2020, Vol. 37 
