引言

磁共振成像（MRI）现在已经广泛应用于临床诊断和科学研究等各个领域.MRI系统一般包括主磁场为水平方向的圆柱式系统和主磁场为垂直方向的开放式系统.其中，开放式MRI系统为患者提供了更为舒适的检查环境.

通常来说，MRI系统的梯度磁场由沿着直角坐标系三个坐标轴的线性梯度磁场组成，通过施加不同的脉冲序列，实现选层、频率编码和相位编码的功能.MRI系统的梯度磁场由特定的梯度线圈生成，梯度线圈的设计方法也在不断发展和改进.1984年，Edelstein等^[1]提出通过构造特定的流函数，求解梯度线圈所在平面的电流密度分布；1986年，Turner等^[2]通过对设定的梯度磁场反向求解得到电流密度分布，再使用流函数法对电流密度分布进行离散化，这类方法也被称为目标场法；之后，Bowtell等^[3]提出了最小功耗约束下的目标场法；Yoda^[4]提出了双平面梯度线圈的目标场法推导过程.这些设计方法都是为了设计出非固定形状的、每个方向对应一个线圈的梯度线圈.2010年，Juchem等^[5]通过Levenberg-Marquardt法，求解了由一组线圈组成的梯度线圈系统；之后，Jia等^{[6, 7]}将这种类型的梯度线圈系统称为矩阵式梯度系统，并对其生成非线性梯度磁场的可行性进行了研究.2018年，Kroboth等^[8]将矩阵式梯度线圈的设计视为一个广义分配问题，并利用模拟退火法对矩阵式线圈进行设计.相比于传统的梯度线圈，矩阵式梯度线圈中的每一个线圈都对梯度磁场有一定的贡献，具有非常高的灵活性，可用于生成不同形态的梯度磁场；而且相较于传统梯度线圈所需的较大电流与散热条件相比，矩阵式梯度线圈更安全，也更适用于各种不同的环境.

Levenberg-Marquardt法是一种局部寻优算法，具有较快的收敛速度，但非常依赖初始值的设定；而粒子群算法是一种模拟仿生算法，能够进行全局最优搜索，对初始值的依赖程度不高.

本文通过粒子群算法与遗传算法设计了一种应用于开放式MRI系统下的矩阵梯度线圈系统，并通过有限元仿真验证了设计的有效性，结果表明所设计的矩阵式梯度线圈具有较好的线性度.

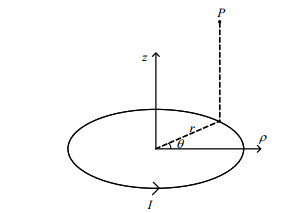
1 梯度磁场的计算与梯度线圈设计 1.1 梯度磁场的计算

矩阵式梯度磁场由许多大小相同的圆形线圈组成.根据磁场叠加定理，各个圆形线圈所生成的磁场叠加后，可以得到最终的梯度磁场.对于闭合的单个圆线圈，以线圈中心点处的轴为中心轴，建立柱坐标系（图 1），P点坐标为(r, θ, Z)，令φ = (π +θ)/2.

设P点处的磁感应强度为B.将分解为纵向分量B_Z和横向分量${B_\rho }$，并且只需要计算z方向上的磁感应强度B_Z：

$ {B_Z} = \frac{{{\mu _0}I}}{{2{\rm{ \mathsf{ π} }}\sqrt {{Z^2} + {{(r + \rho )}^2}} }}\left[ {K(k) - \frac{{{Z^2} - {r^2} + {\rho ^2}}}{{{Z^2} + {{(r - \rho )}^2}}}E(k)} \right] $

(1)

其中，$k = \sqrt {\frac{{4r\rho }}{{{Z^2} + {{(r + \rho )}^2}}}} $，$K(k) = \int_0^{{\rm{ \mathsf{ π} }}/2} {\frac{{{\rm{d}}\phi }}{{\sqrt {1 - {k^2}{{\sin }^2}\phi } }}} $，$E(k) = \int_0^{{\rm{ \mathsf{ π} }}/2} {\sqrt {1 - {k^2}{{\sin }^2}\phi } {\rm{d}}\phi } $，r为该线圈的半径，Z与ρ分别是P点在柱坐标系下的坐标，I为线圈中通过的电流，${\mu _0}$为空气中的磁导率，ϕ为第一类与第二类完全椭圆积分的被积项.

对于N匝线圈，在某一点P处的纵向磁感应强度为

$ {B_{ZN}} = \frac{{{\mu _0}IN}}{{2{\rm{ \mathsf{ π} }}\sqrt {{Z^2} + {{(r + \rho )}^2}} }}\left[ {K(k) - \frac{{{Z^2} - {r^2} + {\rho ^2}}}{{{Z^2} + {{(r - \rho )}^2}}}E(k)} \right] $

(2)

对于由n个圆形线圈组成的矩阵式梯度系统而言，在任意一点P处z方向上的磁感应强度为

$ {B_Z} = \sum\limits_{i = 1}^n {\frac{{{\mu _0}{I_i}{N_i}}}{{2{\rm{ \mathsf{ π} }}\sqrt {{Z_{wi}}^2 + {{({r_i} + {\rho _{wi}})}^2}} }}} \left[ {K({k_{wi}}) - \frac{{{Z_{wi}}^2 - {r_i}^2 + {\rho _{wi}}^2}}{{{Z_{wi}}^2 + {{({r_i} - {\rho _{wi}})}^2}}}E({k_{wi}})} \right] $

(3)

其中，$({\rho _{wi}}, {\theta _{wi}}, {Z_{wi}})$为以成像区域的中心建立世界柱坐标系下的P点坐标，在世界坐标系下第i个线圈圆心坐标为$({\rho _{ci}}, {\theta _{ci}}, {Z_{ci}})$，设$({\rho _i}, {\theta _i}, {Z_i})$为以第i个线圈圆心建立的柱坐标系下的柱坐标，则有

$ ({\rho _{wi}}, {\theta _{wi}}, {Z_{wi}}) = \left[ {\rho _{ci}^2 + \rho _i^2 + 2{\rho _{ci}}{\rho _i}\cos ({\theta _{ci}} - \theta ), \arctan \left( {\frac{{{\rho _{ci}}\sin {\theta _{ci}} + {\rho _i}\sin {\theta _i}}}{{{\rho _{ci}}\cos {\theta _{ci}} + {\rho _i}\cos {\theta _i}}}} \right), {Z_{ci}} + {Z_i}} \right] $

(4)

1.2 矩阵式梯度线圈的结构设计

本文设计的永磁式矩阵梯度磁场系统的成像区域为直径100 mm的球形区域，上下极板的距离为200 mm.用于产生x方向上的梯度磁场的矩阵式梯度线圈共有224个，每个线圈外直径为40 mm、内直径为37 mm，采用直径为1 mm的铜漆包线绕制而成，线圈层数为3，匝数为30，高度为10 mm.用于产生y方向和z方向上的梯度磁场的矩阵式梯度线圈规格与之相同.梯度磁场的梯度大小为10 mT/m.以x方向的梯度线圈为例，矩阵式梯度线圈如图 2所示.

1.3 局部粒子群-遗传优化算法设计

本文使用粒子群算法与遗传算法结合的优化算法^[9]对矩阵式梯度线圈系统中每个线圈的电流值进行了优化设计.该方法以局部粒子群优化算法为基础，并利用遗传算法选择局部最优个体，避免陷入局部最优.每个线圈的安匝数作为粒子群中的一个粒子，衡量粒子群的适应度函数为：

$ \begin{array}{l} Fitness = \sum\limits_{i = 1}^M {\frac{{\left| {{B_{Zi}}({I_1}, {I_2}, \cdots , {I_n}) - {B_{Z{\rm{set}}}}} \right|}}{{{B_{Zset}}}}} \\ s.t.{\rm{ }}\;\;\;\; - {I_{\max }} \le {I_j} \le {I_{\max }} \end{array} $

(5)

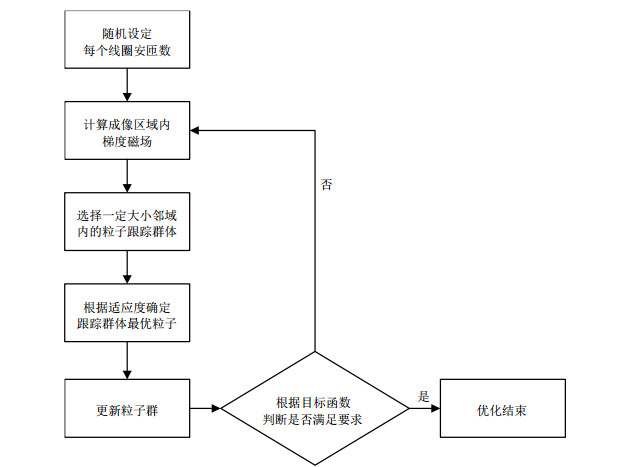
其中，I_j是第j个线圈的电流大小，n为线圈的数量，M为成像区域中选取参考点的数量，B_Zi为第i个参考点处z方向上的磁感应强度，B_Zset是设定的z方向上的目标磁感应强度，约束条件中，I_max为设定的最大电流值.具体的步骤（流程图如图 3所示）如下：

步骤一：如果当前迭代次数t=T，或适应度大于设定值F_set，结束迭代过程；

步骤二：计算各个粒子$P_i^t = (x_{i1}^t, x_{i2}^t, \cdots , x_{id}^t, \cdots , x_{in}^t)$的适应度Fitness，其中$x_{id}^t$是第t次迭代中第i个粒子中的第d个线圈的电流值；

步骤三：对于每个粒子，选取距离为k的邻域作为粒子跟踪群体.其中，$k = gt + {k_b}$，会随着迭代次数的增加而增加，最终使得粒子跟踪群体为整个粒子群；

步骤四：对于每个粒子，以粒子跟踪群体内各个粒子的历史最优适应度（$F_{{\rm{best}}}^t$）作为生存概率，得到一个经过遗传选择的粒子跟踪群体最优粒子$P_{{\rm{best}}}^t = (x_{{\rm{best}}1}^t, x_{{\rm{best}}2}^t, x_{{\rm{best}}3}^t, \cdots , x_{{\rm{best}}n}^t)$并根据$P_{{\rm{best}}}^t$计算得到新的各个粒子的历史最优适应度$F_{{\rm{best}}}^t$；

步骤五：对于每个粒子$P_i^t = (x_{i1}^t, x_{i2}^t, x_{i3}^t, \cdots , x_{in}^t)$，计算其位置速度更新向量$v_{id}^{t + 1}$，并得到新的粒子$P_i^{t + 1} = (x_{i1}^{t + 1}, x_{i2}^{t + 1}, x_{i3}^{t + 1}, \cdots , x_{in}^{t + 1})$，计算方式为

$ v_{id}^{t + 1} = \omega v_{id}^t + {c_1}\xi ({x_{i{\rm{best}}d}} - x_{id}^t) + {c_2}\eta (x_{{\rm{best}}d}^t - x_{id}^t) $

(6)

$ x_{id}^{t + 1} = x_{id}^t + rv_{id}^{t + 1} $

(7)

其中，${P_{i{\rm{best}}}} = ({x_{i{\rm{best}}1}}, {x_{i{\rm{best2}}}}, {x_{i{\rm{best3}}}}, \cdots , {x_{i{\rm{best}}n}})$是每个粒子的历史最优适应度粒子，ω为惯性权重，c₁为认知权重，c₂为社会权重，ξ和η为[0, 1]内的随机数，r为约束因子；

步骤六：返回步骤一继续迭代.

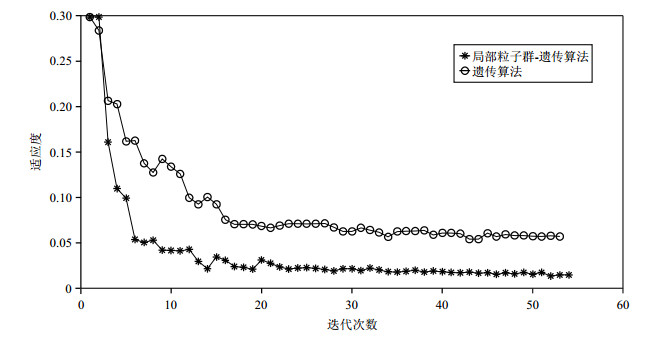
2 结果与讨论 2.1 局部粒子群-遗传优化算法的性能

本文使用Matlab对梯度磁场数值进行计算并优化得到设计方案.为了对比使用遗传算法和局部粒子群-遗传优化算法性能的差异，按表 1所示的参数对两种算法进行了对比，局部粒子群-遗传算法的遗传算法部分的变异概率与交叉概率参数与表中遗传算法参数相同，结果如图 4所示.可以看到，与遗传算法相比，局部粒子群-遗传算法具有更高的收敛速度.

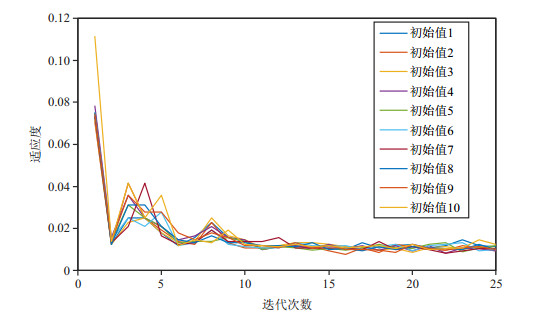
为了验证不同初始值对于局部粒子群-遗传优化算法的影响，本文使用10组不同的随机初始值进行了测试（图 5）.结果表明，本优化算法对于初始值的依赖性较小.

2.2 x、y方向的矩阵梯度线圈

对于x方向的梯度磁场，设定上下两个极板上的对应线圈电流相等；但是在同一平面上，关于y轴对称的线圈的电流值方向相反.y方向的矩阵梯度磁场系统设计方案与x方向相同，只需将x方向的设计方案绕z轴旋转90˚即可.经过计算得到的设计结果如图 6所示.

为了验证设计方案的有效性，本文利用多物理场仿真软件Comsol 5.0（Comsol Inc.瑞典）建立了对应的线圈模型，并使用设计方案中的线圈参数进行仿真计算.利用Comsol软件中的FGMRES求解器计算得到的梯度磁场在成像区域中的均匀性，以(8)式计算非均匀性值δ来衡量梯度磁场的均匀性，当最大δ小于5%时，磁场具有较好的均匀度：

$ \delta = \sum\limits_{DSV} {\frac{{\left| {{B_Z} - {B_{Z{\rm{set}}}}} \right|}}{{{B_{Z{\rm{set}}}}}}} $

(8)

计算得到本文设计方案中成像区域中平均非均匀性值为0.851%，最大非均匀性值为4.5%，达到了目前主流设计方法最大非均匀性值< 5%的设计水平.

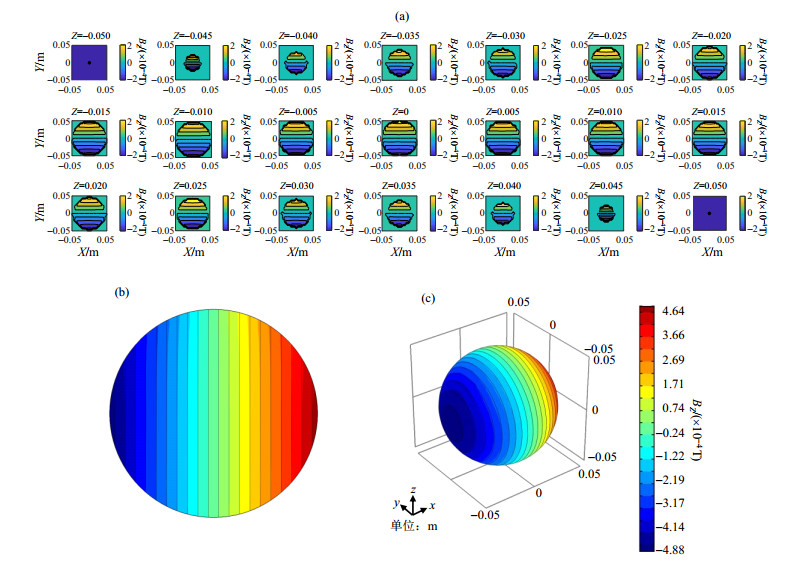
在优化设计阶段计算得到的梯度磁场分布如图 7(a)所示.利用Comsol多物理场仿真软件仿真得到的梯度磁场如图 7(b)、7(c)所示.图 7(a)中，展示了每隔5 mm，对成像区域中y-x平面上的梯度磁场分布情况，可以看到在不同高度的平面处，梯度磁场均匀性均较高.图 7(b)展示了利用Matlab 2014b（Math Works，美国）数值计算方法计算设计方案，在成像区域的中间位置，即Z=0处，x-y平面的梯度磁场分布情况.图 7(c)展示了整个成像区域的梯度磁场.图 7(b)、7(c)中的黑色实线为设定的梯度磁场等值线.所有线圈中的最大电流值为11.33 A.

2.3 z方向上的矩阵梯度线圈

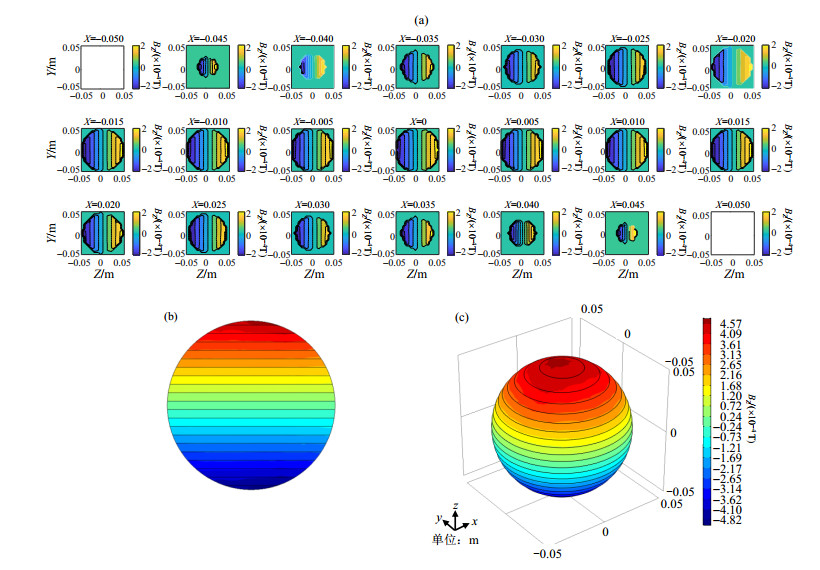
对于z方向的梯度磁场，设定上下两个极板上的对应线圈电流大小相等，方向相反.通过多物理场仿真计算软件Comsol仿真计算得到成像区域中平均非均匀性值为1.013%，最大非均匀性值为4.8%，达到了成像区域最大非均匀度 < 5%的设计水平.在优化设计阶段计算得到的梯度磁场分布如图 8(a)所示.利用Comsol多物理场仿真软件仿真得到的梯度磁场如图 8(b)、8(c)所示.图 8(a)中，展示了每隔5 mm，成像区域中y-z平面上的梯度磁场分布情况，可以看到在不同高度的平面处，梯度磁场的都有较高的均匀性.图 8(b)展示了在成像区域的中间位置，即X=0处，z-y平面的梯度磁场分布情况.图 8(c)展示了整体成像区域的梯度磁场.图 8(b)与图 8(c)中的黑色实线为设定的梯度磁场等值线.所有线圈中的最大电流值为11.33 A.

3 结论

本文设计了适用于平板永磁式MRI系统的矩阵式梯度线圈，并结合粒子群与遗传算法，对矩阵式梯度线圈电流值进行了优化设计.通过全局寻优算法，避免优化陷入局部寻优，并且减少对于初始值的依赖性.仿真计算验证了本文的设计结果在三个梯度方向上均获得了较好的均匀性.本文的研究还存在一些不足，例如，没有将线圈的功率和电感作为优化指标，接下来可以将其作为优化内容进一步改进矩阵式梯度线圈系统.此外，优化算法也需要进一步改善，除了改进优化过程中的各个参数外，还可以研究更适用于矩阵式梯度线圈优化设计的算法.