核磁共振(nuclear magnetic resonance,NMR)技术是一种用途广泛、获得信息丰富的分析技术,应用范围包括人体及小动物成像、分子结构和动力学研究、食品检测等.但目前的研究对分析技术精度的要求越来越高,灵敏度较低这一不足在一定程度上限制了NMR技术的发展和应用.NMR检测灵敏度较低的主要原因是在热平衡状态下,核自旋能级之间粒子数的差异太小.为了提高NMR检测灵敏度,研究者们提出了一系列的方法,例如针对液态自旋体系,溶解动态核极化(dissolution-dynamic nuclear polarization,d-DNP)和仲氢诱导极化(parahydrogen-induced polarization,PHIP)[1-4]等手段都使NMR信号得到了较大增强.但被极化的核自旋仍然面临极化度衰减的问题,即无论核自旋的极化度被提高了多少倍,其存在的时间难以超过本身的纵向弛豫时间(T1),这种衰减是不可逆转的,该特点限制了被极化的核自旋的潜在应用价值.
长寿命核自旋单重态(long-life nuclear spin singlet state,LLS)具有比T1长得多的弛豫时间,这为克服弛豫导致的一些限制提供了机会[5-7].LLS存在于二自旋体系或更多自旋的体系.由于自旋对称性,核自旋单重态受偶极-偶极弛豫的影响较小.当偶极-偶极弛豫主导核自旋的弛豫过程时,核自旋单重态常常具有较长的弛豫时间.自Levitt课题组[5, 6, 8]发现单重态NMR以来,已有许多研究小组对单重态NMR领域进行了研究,目的是定义和表征单重态弛豫特性[9-13]及其存在的条件[14-17];同时证明多自旋体系[18-24],包括同核、异核体系[25]中LLS存在的可能性.除此之外,可制备LLS的化学物质种类也被不断扩展,目前1H核体系[26]的核自旋单重态寿命(TS)可达到10 min以上,13C核[27]的TS可达到约70 min,15N核[28]的TS可达到约26 min.这些核自旋单重态的TS比其对应的T1提高了几倍到几十倍.而LLS由于具有寿命较长这一特性,已被广泛应用于研究分子性质或慢分子运动、化学交换、磁共振成像(magnetic resonance imaging,MRI)和量子计算等领域[29-35].近年来,这种核自旋单态还被应用于模拟鸟类导航[36-38].
核自旋单重态的TS与其使用的制备脉冲密切相关.本文以一个三肽分子(alanylglycylgcine,AGG)的水溶液为例,利用自旋锁定诱导交叉(spin-lock induced crossing,SLIC)脉冲序列[39]制备AGG分子末端-CH2基团中的二个氢原子核自旋体系的LLS,并探究了样品浓度、温度、射频发射中心、自旋体系之间的J耦合值,以及磁场不均匀性五个因素对其转化效率和TS的影响.
1 理论部分图 1所示是制备二自旋体系核自旋单重态的SLIC脉冲序列[39].其中,第一个脉冲为90°硬脉冲,τSL为选择性脉冲(方波)施加的时间,g1和g2为梯度场,CW代表长时间的连续波去耦脉冲,τm表示CW去耦的时间.
上述脉冲序列的算符演化如下:
当待测样品置于磁场中时,体系(以强耦合二自旋为例)处于热平衡状态:
| ${\rho_0} = {\hat I_{1z}} + {\hat I_{2z}}$ | (1) |
其中
经过90° y方向的硬脉冲后,体系的状态变为:
| ${\rho_1} = {\hat I_{1x}} + {\hat I_{2x}}$ | (2) |
其中
在施加长时间选择性脉冲的期间,体系的哈密顿量为:
| $\hat H = {\omega _1}{\hat I_{1z}} + {\omega _2}{\hat I_{2z}} + 2{\rm{ \mathsf{ π} }}{J_{12}}{\hat I_1} \cdot {\hat I_2} + 2{\rm{ \mathsf{ π} }}{J_0}({\hat I_{1x}} + {\hat I_{2x}})$ | (3) |
| ${\hat I_1} \cdot {\hat I_2} = {\hat I_{1x}}{\hat I_{2x}} + {\hat I_{1y}}{\hat I_{2y}} + {\hat I_{1z}}{\hat I_{2z}}$ | (4) |
其中,将射频中心放置在两个核的信号峰中间后,
在演化过程中,当体系的J耦合大小为
| $\begin{gathered} {\rho _3} = \frac{1}{2}({{\hat I}_{1x}} + {{\hat I}_{2x}})- \frac{1}{2}(2{{\hat I}_{1x}}{{\hat I}_{2x}} + {{\hat I}_{1y}}{{\hat I}_{2y}} + {{\hat I}_{1z}} + {{\hat I}_{2z}}) \\ {\rm{ }} = \frac{1}{2}({{\hat I}_{1x}} + {{\hat I}_{2x}})+ \left| {\left. {{S_0}} \right\rangle } \right.\left\langle {\left. {{S_0}} \right| - } \right.\frac{1}{2}\left| {\left. {{T_0}} \right\rangle } \right.\left\langle {\left. {{T_0}} \right| + } \right.{\mathit \Delta} \\ \end{gathered} $ | (5) |
| ${\rho _{{S_0}}} = \left| {\left. {{S_0}} \right\rangle } \right.\left\langle {\left. {{S_0}} \right| = } \right.\frac{E}{2} - {\hat I_{1x}}{\hat I_{2x}} - {\hat I_{1y}}{\hat I_{2y}} - {\hat I_{1z}}{\hat I_{2z}}$ | (6) |
| ${\rho _{{T_0}}} = \left| {\left. {{T_0}} \right\rangle } \right.\left\langle {\left. {{T_0}} \right| = } \right.\frac{E}{2} + {\hat I_{1x}}{\hat I_{2x}} + {\hat I_{1y}}{\hat I_{2y}} - {\hat I_{1z}}{\hat I_{2z}}$ | (7) |
| ${\mathit \Delta} = - \frac{1}{2}\left( {\left| {\left. {{T_1}} \right\rangle } \right.\left\langle {\left. {{T_1}} \right| + } \right.\left| {\left. {{T_1}} \right\rangle } \right.\left\langle {\left. {{T_{ - 1}}} \right| + } \right.\left| {\left. {{T_{ - 1}}} \right\rangle } \right.\left\langle {\left. {{T_1}} \right| + } \right.\left| {\left. {{T_{ - 1}}} \right\rangle } \right.\left\langle {\left. {{T_{ - 1}}} \right|} \right.} \right)$ | (8) |
其中
此时,以
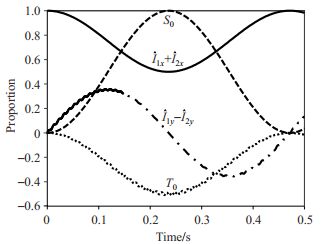
|
图 2 脉冲施加过程中基算符中各项所占比例随演化时间改变的曲线图.因未归一化,单重态所占比例不代表实验中实际转化效率 Fig. 2 A graph showing the proportion of each part of the total operator as a function of evolution time |
| ${\tau _{{\rm{SL}},\max }} = \frac{1}{{\Delta {\rm{v}}\sqrt 2 }} = \frac{{0.707}}{{\Delta {\rm{v}}}}$ | (9) |
τSL为选择性脉冲施加的时间,最大值选取的具体推导过程见文献[40].
图 2曲线表示密度算符
NMR样品管和D2O购自青岛腾龙微波科技有限公司,AGG购自杰北欧生物试剂有限公司.
分别配制浓度为2 mg/mL、4 mg/ mL、8 mg/ mL、16 mg/ mL的AGG-D2O溶液
2.2 NMR实验LLS的NMR实验制备在AVANCE III 500型液体NMR谱仪(Bruker)上完成.温度为23 ℃时,对AGG样品结构中的cc'自旋对施加图 1所示的SLIC脉冲序列制备LLS.实验参数设置为:射频中心o1对准目标峰3.97 ppm;采样谱宽(SW)为6 000 Hz;循环等待时间(d1)为5 s;90°和选择性脉冲宽度分别为9.4 μs和12 500 μs,选择性脉冲的功率为50 dB.梯度脉冲g1和g2分别为(800 μs, 20%)和(800 μs, 10%),采用CW去耦,累加次数(NS)为1.
与此同时,分别探究了样品浓度(2 mg/mL、4 mg/ mL、8 mg/ mL、16 mg/ mL)、温度(考虑到样品溶质与溶剂的化学性质,将实验温度分别设置为3 ℃、13 ℃、23 ℃、33 ℃)、磁场的不均性(以NMR信号的半高宽来衡量)、射频发射中心o1(向左分别偏置0 Hz、5 Hz、10 Hz和15 Hz)以及J耦合值对单重态转化效率和TS的影响.
采用反转恢复法测得T1,d1为10 s,采样时间(aq)为2.5 s,NS为8,直接维采样点数(td1)为5 000,间接维采样点数(td2)为16.
3 结果与讨论 3.1 AGG分子的LLS的制备与TS探究图 3(a)和3(b)所示分别为AGG氘水溶液的分子结构和1H NMR谱图(实验参数SW、d1、90°脉宽、NS与2.2节所述相同).两对自旋质子对的谱峰分别位于:Hb和Hb'(q,δH4.04),Hc和Hc'(s,δH3.97).其余质子分别位于:Ha(q,δH4.15),甲基(d,δH1.55).强耦合体系的两个质子分别标记为Hc和Hc'.通过反转恢复法测得该质子对的T1为(1.1±0.1)s.
施加SLIC脉冲序列,对δH3.97处cc'质子对制备核自旋单重态,获得单态信号的NMR谱图如图 3(c)所示.在单重态谱图上,只有cc'质子对的单态信号留下来,并且水峰变得非常小.这是由于单态不受梯度场影响,在如图 1脉冲序列b处和c处分别加一个不同强度的梯度场,将对其它非单态信号进行散相,只保留单态信号.图 3(c)中,bb'质子对信号依然存在,但强度很小,是因为其自旋体系J耦合值与cc'质子对非常接近,在制备目标峰单重态的过程中,bb'自旋对的一部分信号也会保留下来.实验结果表明利用核自旋单态不受梯度场影响的特性可以对特定基团信号进行观测.
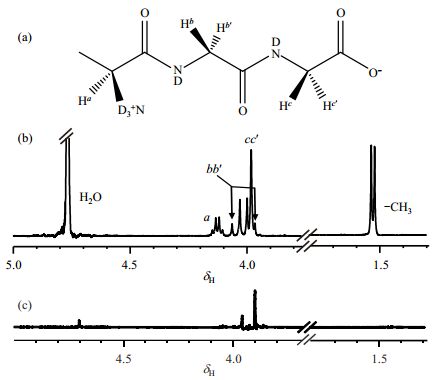
|
图 3 (a) AGG氘水溶液的分子结构;(b)AGG氘水溶液的1H NMR谱图(500 MHz);(c)对δH3.97处cc'质子对制备核自旋单重态得到的NMR谱图 Fig. 3 (a)Molecular structure of AGG in D2O solution; (b)1H NMR spectrum of AGG in D2O solution (500 MHz); (c)1H NMR spectrum obtained by preparing the nuclear spin single state of cc' proton pair at δH3.97 |
LLS最重要的特性是其寿命较长,即NMR谱峰信号衰减常数TS远大于其T1.实验中对制得的单重态自旋核的TS进行测量,通过改变CW去耦的时间τm,采集一系列谱图,通过单指数拟合测得TS为(18.7±0.3)s,约是T1的16.5倍.T1和TS具体拟合曲线见图 4.

|
图 4 AGG氘水溶液位于δH3.97处的质子谱峰面积随演化时间的衰减曲线.(a)正方形为利用反转恢复法测量T1时采集到的数据点,实线是相应的指数衰减拟合曲线,测得T1=(1.1±0.1)s.A1为拟合后归一化面积最大值,A2=2A1;(b)正方形为测量TS时采集到的数据点,实线是相应的指数衰减拟合曲线,测得TS=(18.7±0.3)s.A为拟合后归一化面积最大值.所有信号的积分面积以第一个数据点对应的积分面积进行归一化 Fig. 4 Decay of 1H NMR normalized signal area at δH3.97 for AGG in D2O solution as a function of the CW time. (a)The squares correspond to the normalized signal area from experimental spectrum when measuring T1 by the inversion recovery method. The solid line is the curve obtained by exponential decay fitting, T1=(1.1±0.1)s. A1 is the maximum normalized signal area after fitting, A2=2A1; (b)The squares correspond to the normalized signal area from experimental spectrum when measuring TS. The solid line is the curve obtained by exponential decay fitting, TS=(18.7±0.3)s. A is the maximum normalized signal area after fitting. All signal areas were normalized to the first data point |
在23 ℃下,分别对2 mg/mL、4 mg/ mL、8 mg/ mL和16 mg/ mL四个浓度的AGG溶液中强耦合体系cc'质子对的LLS进行制备,并分别测量其TS,各浓度样品的TS拟合曲线如图 5(a)所示.如图 5(b)和5(c)所示,以2 mg/mL浓度的样品为例,对其1H NMR谱中cc'质子对的信号和制备的核自旋单重态的信号分别进行积分,将后者与前者的比值定义为LLS的转化效率.
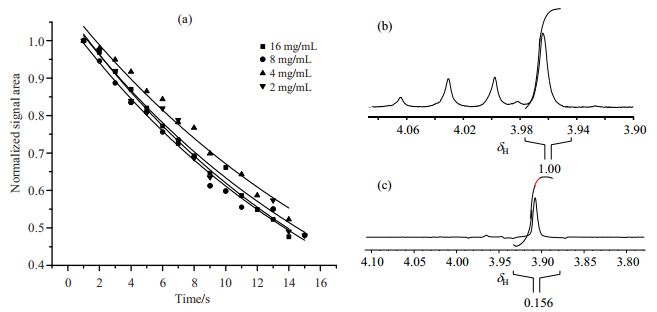
|
图 5 (a) 不同浓度的样品的LLS的TS拟合曲线,所有信号的积分面积以第一个数据点对应的积分面积进行归一化;浓度为2 mg/mL的AGG氘水溶液cc'质子对在(b)1H NMR谱和(c)核自旋单重态的NMR谱中的谱峰积分 Fig. 5 (a)TS fitting curves of LLSs with different concentrations, all signal areas were normalized to the first data point; The normalized signal areas of cc' proton pair in AGG molecule in D2O (2 mg/mL)from (b)1H NMR spectrum and (c)LLS NMR spectrum |
各个样品浓度下,核自旋单重态转化效率和TS如表 1所示.从表 1数据可得,在本实验讨论的浓度范围内,LLS的转化效率和TS均基本一致,在误差范围内.说明在本文实验条件下,LLS的转化效率及TS均不受样品浓度的影响.
| 表 1 不同浓度的AGG分子中cc'质子对的LLS的转化效率和TS(500 MHz,23 ℃) Table 1 Conversion efficiencies and TS values of LLSs from cc' proton pair in AGG molecules with different concentrations (500 MHz, 23 ℃) |
在此基础上,可将研究对象扩展到更高浓度的样品.此时样品溶液中可能存在二聚体、三聚体甚至多聚体.然而因LLS不受分子内部偶极-偶极弛豫影响的独特性质,故而我们推测该核自旋单重态可以在高浓度的样品中成功制备,进而可以将该方法应用于自组装体系,例如蛋白结构中,对局部高浓度的信号进行检测.
3.2.2 温度的影响对浓度为8 mg/mL的AGG样品,在不同的温度下制备LLS,并测量转化效率和TS(图 6和表 2).LLS的转化效率随着温度的降低而不断减小,原因在于实验所用的脉冲序列是依据23 ℃温度下分子的J耦合和化学位移差值进行理论计算得到的,此时两个核自旋之间的化学位移之差为5 Hz.而随着温度的降低,化学位移差值变大,J耦合也发生了一定的变化,因而对应的最佳制备参数应该发生改变.如果脉冲序列不进行调整,仍然使用23 ℃温度下脉冲参数,则会导致获得的LLS转化效率明显降低.但是,当温度高于23 ℃时,化学位移差值进一步变小,此时的脉冲序列对更小的化学位移差并不敏感,因而LLS的转化效率不会发生较大的降低.随着温度的增加,LLS的TS不断增加,表明LLS的TS受温度影响较大.
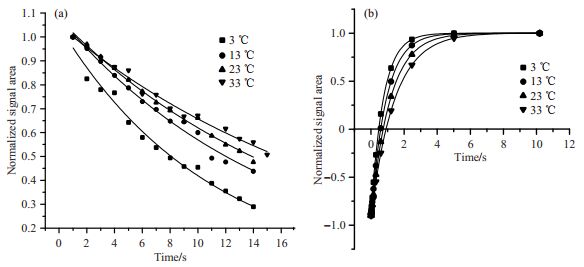
|
图 6 (a) 不同温度下LLS的TS拟合曲线;(b)不同温度下cc'质子对的T1拟合曲线.所有信号的积分面积以第一个数据点对应的积分面积进行归一化 Fig. 6 (a)TSfitting curves of LLS at different temperatures; (b)T1 fitting curves for cc' proton pair at different temperatures. All signal areas were normalized to the first data point |
| 表 2 不同温度下,AGG分子中cc'质子对的LLS的转化效率、TS和T1(500 MHz,8 mg/mL) Table 2 Conversion efficiencies, TS and T1 values of LLSs from cc' proton pair in AGG molecules at different temperatures (500 MHz, 8 mg/mL) |
图 6(b)为cc'质子对的T1拟合曲线,结果显示其T1随温度升高而增加.温度影响T1的物理机制可由BPP理论弛豫机制[41]来解释.根据BPP理论,T1的温度依赖性分低温端和高温端.在低温端,T1随温度的升高不断减小;在高温端,T1随温度的升高不断增加.通常来说,大分子样品由于运动相关时间长而处于低温端,当实验温度升高时,T1呈减小趋势.而小分子样品由于运动相关时间短而处于高温端,当实验温度升高时,T1具有增加趋势.本文使用的AGG为小分子物质,其T1会随温度升高而增加.
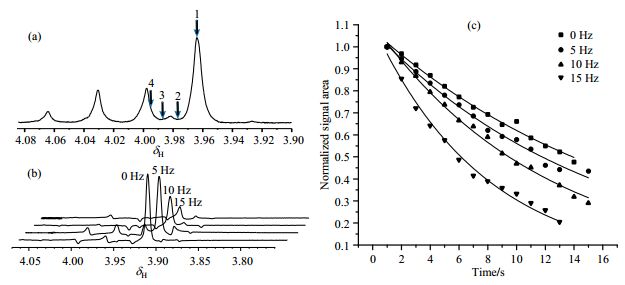
3.2.3 射频发射中心的影响制备过程中发射中心o1位置能够影响LLS的制备效率.本实验中使用浓度为8 mg/mL的样品,温度为23 ℃.一般情况下,在制备LLS过程中,射频中心对准的是δH3.97(Hc和Hc')信号的中心位置,即图 7(a)中1的位置.将o1的位置向左分别偏置5 Hz、10 Hz和15 Hz,即图 7(a)中2、3、4的位置,再进行相同的实验,获得的LLS的1H NMR谱图如图 7(b)所示.图 7(c)为4组偏置情况下LLS的TS拟合曲线.对实验数据进行处理得到如表 3所示的结果.由表 3可知,当o1左偏置5 Hz以内时,LLS的转化效率基本不受影响;而当偏置继续增大的时候,转化效率出现明显下降;可推测当o1偏置大于20 Hz后,基本不能检测到LLS.同时,当o1偏置增大时,LLS的TS不断下降,主要因为射频中心的改变导致非单重态信号夹杂在其中,受其T1弛豫的影响,单指数拟合得到的TS不断下降,而且TS拟合时存在一定误差.
|
图 7 (a) 制备LLS时射频发射中心o1的位置;(b)不同的o1偏置下,LLS的1H NMR谱;(c)不同o1偏置下,LLS的TS拟合曲线,所有信号的积分面积以第一个数据点对应的积分面积进行归一化 Fig. 7 (a)The o1 locations of the radio frequency center for preparation of LLSs; (b)1H NMR spectra of LLSs at different o1 offsets; (c)TS fitting curves of LLSs at different o1 offsets, all signal areas were normalized to the first data point |
| 表 3 不同o1偏置时,AGG分子中cc'质子对的LLS的转化效率和TS(500 MHz) Table 3 Conversion efficiencies and TS values of LLSs from cc' proton pair in AGG molecules at different o1 offsets (500 MHz) |
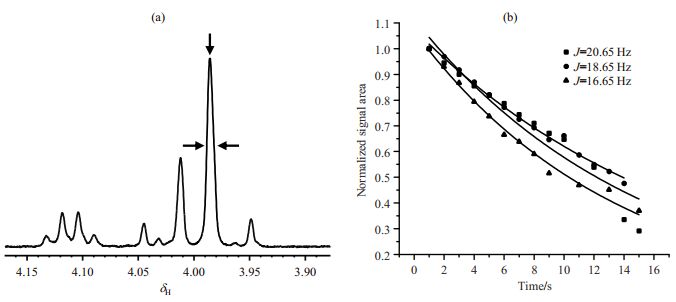
LLS制备的过程中,J耦合值与选择性脉冲功率的设置息息相关,也是决定LLS制备成功与否、效率高低的重要参数.而自旋体系之间的J耦合值一般都是从1H NMR谱中直接读取,这就涉及读取过程中如何选取起始位置.本实验中使用浓度为8 mg/mL的样品,温度为23 ℃.如图 8(a)所示的三个箭头所指的位置,一般情况下,是选取耦合裂分的两个峰的最高位置之间的距离作为J值.故此,在J=18.65 Hz的情况下制备了LLS后,我们分别以目标位置左右两边信号强度的是其一半高度处为基准来读取J耦合值,即在原有读取的J耦合值的基础上加减2 Hz,分别得到J=20.65 Hz和16.65 Hz,并根据此J耦合值分别进行实验,来探究不同的J耦合值对LLS的影响.三组J值条件下测得LLS的TS拟合曲线如图 8(b)所示,转化效率及TS的具体数值见表 4.由表 4可知,当J耦合值发生改变时,不管是增大还是减小,LLS转化效率和TS都明显下降.这表明在LLS制备过程中,J耦合值的精确读取至关重要.TS随J耦合值的变化而降低的原因是单重态信号中包含了其它成分,受其弛豫的影响,测得的TS减小.本研究中,当J=16.65 Hz时,TS拟合误差较大,故而产生更大的偏差.
|
图 8 (a) 1H NMR谱中读取时J值起始点位置的选择;(b)不同J值下,LLS的TS拟合曲线,所有信号的积分面积以第一个数据点对应的积分面积进行归一化 Fig. 8 (a)Selection of the starting point when reading J-coupling value in 1H NMR spectrum; (b)TS fitting curves different J-coupling values. All signal areas were normalized to the first data point |
| 表 4 不同J值时,AGG分子中cc'质子对的LLS的转化效率和TS(500 MHz) Table 4 Conversion efficiencies and TS values of LLSs from cc' proton pair in AGG molecules at different J values (500 MHz) |
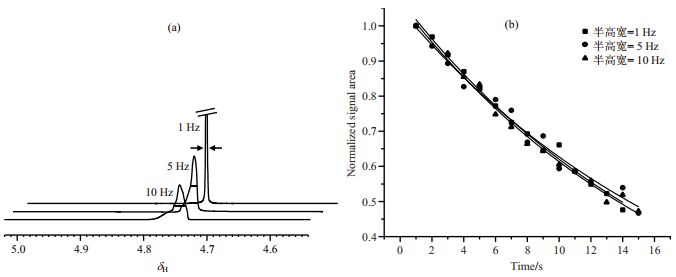
我们进一步使用浓度为8 mg/mL的样品,在23 ℃下,探讨了磁场不均匀性对LLS的影响,磁场不均匀性以谱图中水峰半高宽的大小为衡量标准.本研究涉及的磁场不均匀条件下得到的水的NMR
信号如图 9(a)所示.由于在场不均匀的情况下,NMR谱图分辨率不高,无法精确对1H NMR谱中目标信号进行积分,故而以半高宽为1 Hz时制备得到的LLS信号的积分面积为基准,对其它磁场情况下的LLS信号进行相对积分,以此来衡量不同磁场均匀性下的LLS的相对转化效率.图 9(b)为不同半高宽下,LLS的TS拟合曲线.LLS的相对转化效率及TS的具体见表 5.由表 5可知,磁场不均匀性在在实验设定的范围内,即半高宽在1~10 Hz时,LLS的相对转化效率和TS基本保持一致,在合理的误差范围内波动,表明一定程度的磁场均匀性的改变对LLS转化效率和TS的影响不大.
|
图 9 (a) 不同的磁场均匀性下,水峰信号的半高宽;(b)不同半高宽下,LLS的TS的拟合曲线.所有信号的积分面积以第一个数据点对应的积分面积进行归一化 Fig. 9 (a)At different magnetic field uniformity, the half widths of the water peak signal; (b)TS fitting curves of LLS at different half widths. All signal areas were normalized to the first data point |
| 表 5 不同磁场均匀性下,AGG分子中cc'质子对的LLS的相对转化效率和TS(500 MHz) Table 5 Relative conversion efficiencies and TS values of LLSs from cc' proton pair in AGG molecules at different magnetic field uniformity (500 MHz) |
本文以孤立的二自旋强耦合体系为研究对象、以AGG分子为例,进行了LLS制备及其TS测量,并探讨了样品浓度、温度、射频发射中心、J值和磁场均匀性对LLS转化效率及其TS的影响.研究发现在本实验条件下,LLS的TS随实验温度的升高不断增加.与LLS制备息息相关的实验参数(包括射频发射中心的位置以及J值的选择)则对LLS转化效率和TS有显著影响:o1偏置在小范围内变化时,LLS所受影响不甚明显,但当偏置较大时,其转化效率与TS出现明显减小;LLS的转化效率和TS对J值变化则比较敏感,当J耦合值读取不够精确时,LLS的转化效率和TS都明显降低.磁场的不均匀性对LLS的影响则与样品浓度类似,两者在一定范围变化时,LLS转化效率和TS未出现明显变化.这些结果为LLS制备时实验条件的选择提供了参考,并对长相干态的应用提供理论依据,例如,当用长相干单重态模拟鸟类导航[38]时,通过模拟外界的控制条件,可以进一步探讨外界环境(如磁场变换,温度变化)对导航定位的影响等过程.
| [1] | ARDENKJæR-LARSEN J H, GOLMAN K, GRAM A, et al. Increase of signal-to-noise of more than 10, 000 times in liquid state NMR[J]. Discov Med, 2003, 3(19): 37-39. |
| [2] | ADAMS R W, AGUILAR J A, ATKINSON K D, et al. Reversible interactions with para-hydrogen enhance NMR sensitivity by polarization transfer[J]. Science, 2009, 323(5922): 1708-1711. DOI: 10.1126/science.1168877. |
| [3] | BOWERS C R, WEITEKAMP D P. Parahydrogen and synthesis allow dramatically enhanced nuclear alignment[J]. J Am Chem Soc, 1987, 109(18): 5541-5542. DOI: 10.1021/ja00252a049. |
| [4] |
WANG W Y, HU H, XU J, et al. Hydrogenation reaction on pd-cu bimetallic catalysts:a parahydrogen-induced polarization study[J].
Chinese J Magn Reson, 2018, 35(3): 269-279.
王伟宇, 胡涵, 徐君, 等. Pd-Cu双金属催化剂上加氢反应的仲氢诱导超极化研究[J]. 波谱学杂志, 2018, 35(3): 269-279. |
| [5] | CARRAVETTA M, JOHANNESSEN O G, LEVITT M H. Beyond the T1 limit:singlet nuclear spin states in low magnetic fields[J]. Phys Rev Lett, 2004, 92(15): 153003. DOI: 10.1103/PhysRevLett.92.153003. |
| [6] | CARRAVETTA M, LEVITT M H. Long-lived nuclear spin states in high-field solution NMR[J]. J Am Chem Soc, 2004, 126(20): 6228-6229. DOI: 10.1021/ja0490931. |
| [7] | FENG Y, DAVIS R M, WARREN W S. Accessing long-lived nuclear singlet states between chemically equivalent spins without breaking symmetry[J]. Nat Phys, 2012, 8(11): 831-837. DOI: 10.1038/nphys2425. |
| [8] | CARRAVETTA M, LEVITT M H. Theory of long-lived nuclear spin states in solution nuclear magnetic resonance. I. Singlet states in low magnetic field[J]. J Chem Phys, 2005, 122(21): 214505. DOI: 10.1063/1.1893983. |
| [9] | PILEIO G. Relaxation theory of nuclear singlet states in two spin-1/2 systems[J]. Prog Nucl Mag Res Sp, 2010, 56(3): 217-231. DOI: 10.1016/j.pnmrs.2009.10.001. |
| [10] | PILEIO G, LEVITT M H. Theory of long-lived nuclear spin states in solution nuclear magnetic resonance. II. Singlet spin locking[J]. J Chem Phys, 2009, 130(21): 214501. DOI: 10.1063/1.3139064. |
| [11] | PILEIO G. Singlet state relaxation via intermolecular dipolar coupling[J]. J Chem Phys, 2011, 134(21): 214505. DOI: 10.1063/1.3596379. |
| [12] | PILEIO, G. Singlet state relaxation via scalar coupling of the second kind[J]. J Chem Phys, 2011, 135(17): 174502. DOI: 10.1063/1.3651479. |
| [13] | TAYLER M C D, LEVITT M H. Paramagnetic relaxation of nuclear singlet states[J]. Phys Chem Chem Phys, 2011, 13(20): 9128-9130. DOI: 10.1039/c1cp20471h. |
| [14] | VINOGRADOV E, GRANT A K. Long-lived states in solution NMR:Selection rules for intramolecular dipolar relaxation in low magnetic fields[J]. J Magn Reson, 2007, 188(1): 176-182. DOI: 10.1016/j.jmr.2007.05.015. |
| [15] | PILEIO G, LEVITT M H. J-stabilization of singlet states in the solution NMR of multiple-spin systems[J]. J Magn Reson, 2007, 187(1): 141-145. DOI: 10.1016/j.jmr.2007.03.019. |
| [16] | GRANT A K, VINOGRADOV E. Long-lived states in solution NMR:Theoretical examples in three-and four-spin systems[J]. J Magn Reson, 2008, 193(2): 177-190. DOI: 10.1016/j.jmr.2008.04.030. |
| [17] | KARABANOV A A, BRETSCHNEIDER C, KÖCKENBERGER W. Symmetries of the master equation and long-lived states of nuclear spins[J]. J Chem Phys, 2009, 131(20): 204105-204110. DOI: 10.1063/1.3265852. |
| [18] | PILEIO G, CONCISTRÈ M, CARRAVETTA M, et al. Long-lived nuclear spin states in the solution NMR of four-spin systems[J]. J Magn Reson, 2006, 182(2): 353-357. DOI: 10.1016/j.jmr.2006.06.034. |
| [19] | AHUJA P, SARKAR R, VASOS P R, et al. Long-lived states in multiple-spin systems[J]. Chem Phys Chem, 2010, 10(13): 2217-2220. |
| [20] | MEIER B, DUMEZ J N, STEVANATO G, et al. Long-lived nuclear spin states in methyl groups and quantum-rotor-induced polarization[J]. J Amer Chem Soc, 2013, 135(50): 18746-18749. DOI: 10.1021/ja410432f. |
| [21] | PRAVDIVTSEV A N, YURKOVSKAYA A V, ZIMMERMANN H, et al. Magnetic field dependent long-lived spin states in amino acids and dipeptides[J]. Phys Chem Chem Phys, 2014, 16(16): 7584-7594. DOI: 10.1039/c3cp55197k. |
| [22] | STEVANATO G, SINGHA ROY S, HILL-COUSINS J, et al. Long-lived nuclear spin states far from magnetic equivalence[J]. Phys Chem Chem Phys, 2015, 17(8): 5913-5922. DOI: 10.1039/C4CP05704J. |
| [23] | DUMEZ J N, HẢKANSSON P, MAMONE S, et al. Theory of long-lived nuclear spin states in methyl groups and quantum-rotor induced polarisation[J]. J Chem Phys, 2015, 142(4): 044506. DOI: 10.1063/1.4906273. |
| [24] |
GUO H Q, XIN J X, LIU H X, et al. Preparation of long-lived nuclear singlet states in three-spin systems[J].
Chinese J Magn Reson, 2018, 35(3): 345-352.
郭海清, 辛家祥, 刘慧霞, 等. 三自旋体系长寿命核自旋单重态的制备[J]. 波谱学杂志, 2018, 35(3): 345-352. |
| [25] | EMONDTS M, LEDBETTER M P, PUSTELNY S, et al. Long-lived heteronuclear spin-singlet states in liquids at a zero magnetic field[J]. Phys Rev Lett, 2014, 112(7): 077601. DOI: 10.1103/PhysRevLett.112.077601. |
| [26] | PILEIO G, DUMEZ J N, POP I A, et al. Real-space imaging of macroscopic diffusion and slow flow by singlet tagging MRI[J]. J Magn Reson, 2015, 252: 130-134. DOI: 10.1016/j.jmr.2015.01.016. |
| [27] | STEVANATO G, HILL-COUSINS J T, HẢKANSSON P, et al. A nuclear singlet lifetime of more than one hour in room-temperature solution[J]. Angew Chem Int Ed Eng, 2015, 54(12): 3740-3743. DOI: 10.1002/anie.201411978. |
| [28] | PILEIO G, CARRAVETTA M, HUGHES E, et al. The Long-lived nuclear singlet state of 15N-nitrous oxide in solution[J]. J Amer Chem Soc, 2008, 130(38): 12582-12583. DOI: 10.1021/ja803601d. |
| [29] | AHUJA P, SARKAR R, VASOS P R, et al. Diffusion coefficients of biomolecules using long-lived spin states[J]. J Amer Chem Soc, 2009, 131(22): 7498-7499. DOI: 10.1021/ja902030k. |
| [30] | SARKAR R, VASOS P R, BODENHAUSEN G. Singlet-state exchange NMR spectroscopy for the study of very slow dynamic processes[J]. J Am Chem Soc, 2007, 129(2): 328-334. DOI: 10.1021/ja0647396. |
| [31] | VASOS P R, COMMENT A, SARKAR R, et al. Long-lived states to sustain hyperpolarized magnetization[J]. Pro Natl Acad Sci USA, 2009, 106(44): 18469-14632. DOI: 10.1073/pnas.0908123106. |
| [32] | KOVTUNOV K V, TRUONG M L, BARSKIY D A, et al. Long-lived spin states for low-field hyperpolarized gas MRI[J]. Chemistry, 2014, 20(45): 14629-14632. DOI: 10.1002/chem.201405063. |
| [33] | ROY S S, MAHESH T S. Initialization of NMR quantum registers using long-lived singlet states[J]. Phys Rev A, 2010, 82(5): 3249-3253. |
| [34] | DEVIENCE S J, WALSWORTH R L, ROSEN M S. Probing scalar coupling differences via long-lived singlet states[J]. J Magn Reson, 2016, 262: 42. DOI: 10.1016/j.jmr.2015.12.003. |
| [35] | SALVI N, BURATTO R, BORNET A, et al. Boosting the sensitivity of ligand-protein screening by NMR of long-lived states[J]. J Amer Chem Soc, 2012, 134(27): 11076-11079. DOI: 10.1021/ja303301w. |
| [36] | JONES J A, HORE P J. Spin-selective reactions of radical pairs act as quantum measurements[J]. Chem Phys Lett, 2010, 488(1-3): 90-93. DOI: 10.1016/j.cplett.2010.01.063. |
| [37] | CAI J, CARUSO F, PLENIO M B. Quantum limits for the magnetic sensitivity of a chemical compass[J]. Phys Rev A, 2012, 85(4): 124-130. |
| [38] | PEARSON J, FENG G R, ZHENG C, et al. Experimental quantum simulation of avian compass in a nuclear magnetic resonance system[J]. Sci China Phys Mech, 2016, 59(12): 120312. DOI: 10.1007/s11433-016-0376-6. |
| [39] | DEVIENCE S J, WALSWORTH R L, ROSEN M S. Preparation of nuclear spin singlet states using spin-lock induced crossing[J]. Phys Rev Lett, 2013, 111(17): 173002. DOI: 10.1103/PhysRevLett.111.173002. |
| [40] | FENG Y. Accessing Long-lived nuclear spin states in chemically equivalent spin systems: theory, simulation, experiment and implication for hyperpolarization[D]. Durham: Duke University, 2014. https://www.researchgate.net/publication/281824541_Thesis_Accessing_Long-lived_Nuclear_Spin_States_in_Chemically_Equivalent_Spin_Systems_Theory_Simulation_Experiment_and_Implication_for_Hyperpolarization |
| [41] | MCROBBIE D W, MOORE E A, GRAVESM J, et al. MRI:from picture to proton[M]. New York: Cambridge university Press, 2003. |
 2020, Vol. 37
2020, Vol. 37 

