2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
在传统微波原子频标中,铷原子频标以体积小、功耗低、可靠性高等特点成为应用最广泛的一种频标.它由物理系统和电子线路两部分组成,其中电子线路中产生带调制的微波探询信号(6 834.687 5 MHz ± fM)(Δ=2fM,fM表示最大频偏;Δ表示调制深度)用来激励铷原子产生基态能级之间的跃迁,从而实现共振探测.该微波探询信号通常是由10 MHz压控晶振的信号经过倍频、综合、混频等手段得到.
伴随着电子技术的发展,微波探询信号产生方案有如下几种:1、传统直接模拟倍频技术,一般采用“中频倍频链+微波阶跃管倍频”方案来实现[1],直接模拟倍频技术使用的都是基础模拟元器件,近端相位噪声较好,但是输出杂波较多,电路结构复杂、体积、功耗较大,不便于集成;2、采用“阶跃倍频+直接数字式频率合成器(DDS)混频”实现方案[2, 3],虽然DDS的频率稳定度较高、频率转换时间短,但是DDS输出频率中有较多的频率杂散、输出带宽受限,而且采用该方案制备微波探询信号仍然需连接射频放大器和阶跃恢复二极管,结构较为复杂,整个链路中因各级之间连接所造成的变频损耗和插入损耗不容忽略;3、采用“锁相环(PLL)+DDS”技术实现[4],该方案具体是采用DDS产生低频调制信号,并采用PLL替代阶跃恢复二极管实现整数高次倍频得到带调制的微波信号,不仅信号频谱纯度高、相位噪声低,且输出频率范围宽、调节方便,但是该方案采用DDS和PLL两个分立器件,需要单独控制、结构复杂,且会引入更多的附加噪声.
针对现有方案存在的电路结构复杂、附加相噪大、功耗大、不便于集成的缺点,本文通过采用纯PLL电路,以10 MHz信号作为输入参考时钟,直接输出带调制的微波探询信号,省去了DDS模块因相位截断引入的附加噪声;且采用合理的时序控制屏蔽因相位不连续带来的噪声,使获得的微波信号频谱更纯净;同时,该设计方案电路结构更为简单、功耗更小,为后期铷频标进一步微型化提供思路.
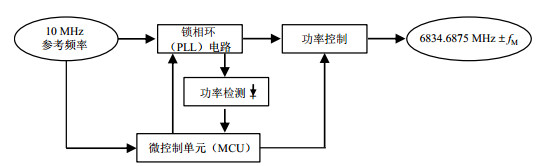
1 微波探询信号的方案设计 1.1 电路设计方案本文设计的微波产生电路方案如图 1所示.10 MHz信号作为微控制单元或称单片机(MCU)和PLL电路的参考频率.MCU用于对PLL的寄存器进行参数、工作时序的配置以及输出微波功率值的采集和控制.PLL的输出分为两路:一路输入功率检测电路中用以检测微波功率的大小;另外一路通过功率控制电路后输出带调制的微波探询信号.
|
图 1 微波产生电路方案 Fig. 1 Scheme of microwave generation circuit |
带调制的微波信号在量子系统跃迁谱线中心频率
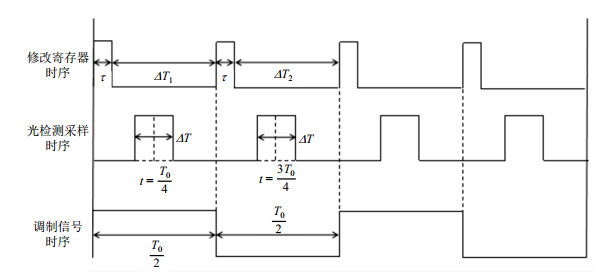
PLL输出频率的跳变时间与寄存器配置有关,通过程序配置的优化,能使PLL在τ = 30 μs内完成频率切换.考虑PLL的频率跳变时间及其非连续相位影响,需要设计合理的时序控制方案屏蔽此影响,本文设计方案中设置的调制信号频率为79 Hz,周期T0 = 12.6 ms,具体的时序控制如图 2所示.其中,τ = 30 μs,表示修改寄存器完成频率切换所用的时间;在ΔT1时间段内PLL输出频率f1=6 834.687 5 MHz+fM,在ΔT2时间段内PLL输出频率为f2=6 834.687 5 MHz-fM.光检测采样时间为ΔT = 2 ms,采样时间的中心时刻设置在
|
图 2 时序控制流程图 Fig. 2 Sequence control flow chart |
本文设计将光检测采样设置在调制信号半周期的中间时段,避开因PLL频率跳变导致相位不连续引入的噪声,预留足够的时间使PLL输出频率稳定并在谐振腔内达到稳态,确保采样准确.
2 微波探询信号的性能分析带调制的微波探询信号需馈入原子钟微波腔内用于激发原子跃迁,其性能是影响铷原子频标指标的重要因素,体现在对短期、长期稳定度的影响.
2.1 微波产生电路附加不稳定度分析由于相位噪声的存在使频率源频率不稳定,铷频标中微波产生电路主要考虑1 s时的附加不稳定度,这种不稳定度常用时域阿仑方差σy(τ)来表征[5].但在短取样时间内,时域测量非常困难且不准确.已有文献[6]报道通过传递函数可将频域稳定度
| $\sigma _y^2(\tau ) = \int_0^\infty {\frac{{{{\sin }^4}({\rm{ \mathsf{ π} }}f\tau )}}{{{{({\rm{ \mathsf{ π} }}f\tau )}^2}}} \cdot {S_y}(f){\rm{d}}f} $ | (1) |
其中,f为傅里叶频率,等于偏离标称频率的值;
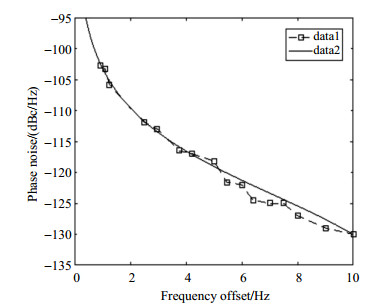
因此对微波产生电路的输入、输出信号进行相位噪声测量,可得到微波产生电路的附加不稳定度.实验中利用相噪测试仪Agilent N5500A对微波产生电路的10 MHz输入信号进行相噪测试,测试结果如图 3所示,图中横坐标Frequency offset即代表(1)式中的f,data1表示相噪测试数据,data2表示利用最小二乘法拟合的曲线,可将其频域频率稳定度表示如下:
| ${S_\phi }{(f)_{{\rm{10 MHz}}}} = 1.05 \times {10^{ - 10}} \cdot {f^{ - 2}} - 8.60 \times {10^{ - 12}} \cdot {f^{ - 1}}$ | (2) |
|
图 3 10 MHz输入信号相噪及其最小二乘法拟合曲线 Fig. 3 Phase noise of 10 MHz input signal and its least square fitting curve |
将(2)式代入(1)式后计算得到微波产生电路10 MHz输入参考时钟的时域频率稳定度为:
| ${\sigma _y}{({\rm{1s}})_{{\rm{10 MHz}}}} = 4.91{\rm{E}} - 13/{\rm{s}}$ | (3) |
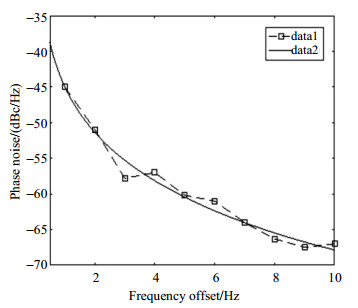
图 4是微波产生电路输出6 834 MHz频率的相噪测试结果,拟合后的频域频率稳定度表达式为:
| ${S_\phi }{(f)_{{\rm{6834 MHz}}}} = 6.91 \times {10^{ - 5}} \cdot {f^{ - 2}} - 5.94 \times {10^{ - 6}} \cdot {f^{ - 1}} + 2.30 \times {10^{ - 7}} \cdot {f^0}$ | (4) |
|
图 4 6 834 MHz输出信号相噪及其最小二乘法拟合曲线 Fig. 4 Phase noise of 6 834 MHz output signal and its least square fitting curve |
将(4)式代入(1)式后计算得到微波产生电路6 834 MHz输出信号的时域频率稳定度为:
| ${\sigma _y}{({\rm{1s}})_{{\rm{6834 MHz}}}} = 5.87{\rm{E}} - 13/{\rm{s}}$ | (5) |
所以该微波产生电路的1 s附加不稳定度由下式计算得到为
| $\sqrt {{\sigma _y}({\rm{1s}})_{{\rm{6834 MHz}}}^2 - {\sigma _y}({\rm{1s}})_{{\rm{10 MHz}}}^2} = \sqrt {{{(5.87{\rm{E}} - 13)}^2} - {{(4.91{\rm{E}} - 13)}^2}} = 3.22{\rm{E}} - 13/{\rm{s}}$ | (6) |
在铷原子频标中,抽运光在进行光泵浦时会产生光位移,该光位移会因吸收泡内光强、微波场强不均匀而沿着光束的路径不断变化,导致共振线的不均匀展宽,使共振谱线的中心频率为所用微波功率的函数,这种效应称为功率频移[7].功率频移表现为当输入腔体内的微波功率变化1 dB时,频标的输出频率会发生E-10量级的变化,即达到1E-12的长期稳定度,则要求微波功率稳定在0.01 dB水平,所以研究并提高微波功率稳定性将有利于改善小型铷原子频标的长期稳定性[7].
温度是影响微波功率稳定性的一个重要因素.温度的变化会影响微波功率幅度,在微波功率频移作用下直接引起铷钟输出频率的变化.因此将微波产生电路置于-35~60 ℃逐渐变化的环境,待每个温度点稳定后对铷钟输出频率进行采集,记录此时的微波功率值,结果如图 5所示.

|
图 5 自动控制前频移和微波功率随温度的变化 Fig. 5 Frequency shift and microwave power varying with temperatures before auto-control |
由图 5中的数据可以得到在全温度范围(-35~60 ℃,ΔT = 95 ℃)内,随着温度的升高,微波功率从-19.91 dBm逐渐减小到-22.50 dBm,变化量ΔP1为-2.59 dBm;而相应的铷钟输出相对频率从-2.45E-10逐渐增大到2.69E-10,变化量为ΔF1为5.04E-10.计算得到微波功率温度敏感性系数、频移系数分别为:
| $\frac{{\Delta {P_1}}}{{\Delta T}} = - 0.027 \;{\rm{dBm}}/℃$ | (7) |
| $\frac{{\Delta {F_1}}}{{\Delta {P_1}}} = - 1.95E - 10/{\rm{dBm}}$ | (8) |
因微波功率频移体现的铷钟温度系数为:
| $\frac{{\Delta {F_1}}}{{\Delta T}} = \frac{{5.04E - 10}}{{95℃}} = 5.3E - 12/℃$ | (9) |
温度的变化使微波功率发生改变,进而导致铷钟输出频率变化,且全温度范围内铷钟频移达到E-10量级.考虑通过对微波功率温度敏感性的控制,使微波功率不随温度发生改变,从而降低铷钟的温度系数.实验中利用MCU对微波功率检测值进行采集并将其与设定功率值进行对比,根据差值大小对功率控制电路进行自动反馈调节,从而达到微波功率稳定的目的,测试结果如图 6所示.从图 6的测试结果可以看出经过对微波反馈控制环路后,在全温度范围内,微波功率变化量ΔP2为0.3 dBm;相应的铷钟频率变化量ΔF2为5.3E-11.计算得到经控制环路后的铷钟频移温度系数为:
| $\frac{{\Delta {F_2}}}{{\Delta T}} = \frac{{5.3{\rm{E}} - 11}}{{95\, ℃}} = 5.6{\rm{E}} - 13/℃$ | (10) |
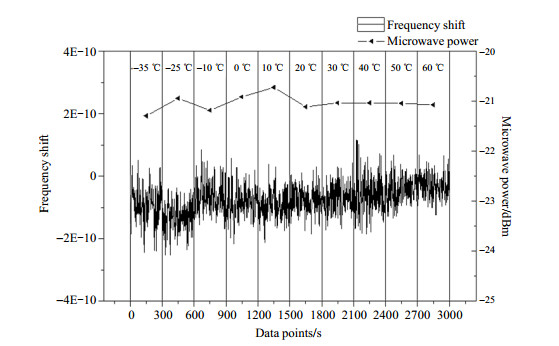
|
图 6 自动控制后频移和微波功率随温度的变化 Fig. 6 Frequency shift and microwave power varying with temperatures after auto-control |
由上述实验结果可以看出,微波功率自动控制环路可以降低其对温度的敏感性,从而有效的改善铷钟输出频率的温度系数.另外该微波功率控制方案相较于控制温度使微波电路输出功率稳幅的方案[8],不仅降低了电路的复杂程度和功耗,也能较好、较精确的改善微波功率稳定性.
3 整机测试结果与分析将该微波产生电路替代原有的射频链路与铷钟整机系统结合,在m=2 000 s内,每秒测得一个相对频差值yk,将测得的相对频差值yk代入到(11)式所示的哈达玛方差(Hadamard deviation)表达式中进行计算.
| $H{\sigma _y}(3, \tau ) = \sqrt {\frac{1}{{6(m - 2)}}\sum\limits_{k = 1}^{m - 2} {{{({y_{k + 2}} - 2{y_{k + 1}} + {y_k})}^2}} } $ | (11) |
将计算结果进行作图得到用哈达玛方差表示的铷钟时域频率稳定度,如图 7所示.

|
图 7 新方案的铷钟频率稳定度 Fig. 7 Frequency stability of rubidium clock with new scheme |
由图 7可得采用本文设计的微波产生电路的铷钟频率稳定度分别为1.19E-11/(1 s)、3.71E-12/(10 s)、1.18E-12/(100 s),该测试结果满足小型化商业铷钟的指标要求.
4 结果与讨论本文介绍了一种利用PLL技术实现非连续微波探询信号的产生方案,通过合理的时序控制避免了相位非连续带来的干扰和影响,附加稳定度低,铷钟频移温度系数可提高至E-13/℃,用该方案实现的铷钟频率稳定度优于
| [1] | 费元春. 固态倍频[M]. 北京: 高等教育出版社, 1985: 79-113. |
| [2] |
HUANG Z, YAN S D, MEI G H, et al. Design and implementation of a new scheme of rubidium atomic frequency standard frequency synthesizer[J].
Chinese J Magn Reson, 2017, 34(4): 481-488.
黄争, 阎世栋, 梅刚华, 等. 一种铷原子频标频率综合器新方案的设计与实现[J]. 波谱学杂志, 2017, 34(4): 481-488. |
| [3] |
LUO Q, BAO W J, QIN L, et al. A small power amplitude stabilization circuit for rubidium atomic frequency standard[J].
Chinese J Magn Reson, 2017, 34(4): 474-480.
罗奇, 包婉静, 秦蕾, 等. 一种小型铷原子频标功率稳幅电路[J]. 波谱学杂志, 2017, 34(4): 474-480. |
| [4] |
FENG K M, WANG L, GUO P X, et al. A new circuit scheme of rubidium vapor chamber frequency standard[J].
Journal of Astronautic Metrology and Measurement, 2004, 24(1): 16-19.
冯克明, 王亮, 郭鹏翔, 等. 一种新型铷汽室频标电路方案[J]. 宇航计测技术, 2004, 24(1): 16-19. DOI: 10.3969/j.issn.1000-7202.2004.01.003. |
| [5] | 巧莉.基于DDS的微波频率源设计与实现[D].成都: 电子科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10614-1013331899.htm |
| [6] | 仲崇霞, 夏振华.短期频率稳定度时频域转换的验证[C]. 2008年全国频率控制技术年会论文集.北京无线电计量测试研究所, 2008: 51-57. |
| [7] | VANIER J, AUDOIN C. The quantum physics of atomic frequency standards[M]. IOP Publishing Ltd, 1989. |
| [8] | 杨世宇, 王世伟, 冯浩, 等.阶跃倍频器温度敏感性对铷原子钟频率稳定度的影响[C].全国时间频率学术会议论文集, 2011: 65-69. |
 2020, Vol. 37
2020, Vol. 37 
