基于深度递归级联卷积神经网络的并行磁共振成像方法

引用本文 [复制中英文]

程慧涛, 王珊珊, 柯子文, 等. 基于深度递归级联卷积神经网络的并行磁共振成像方法[J]. 波谱学杂志, 2019, 36(4): 437-445. DOI: 10.11938/cjmr20192721.

CHENG Hui-tao, WANG Shan-shan, KE Zi-wen, et al. A Deep Recursive Cascaded Convolutional Network for Parallel MRI[J]. Chinese Journal of Magnetic Resonance, 2019, 36(4): 437-445. DOI: 10.11938/cjmr20192721.

[复制英文]

基金项目

国家重点研发计划（2017YFC0108802）

通讯联系人

梁栋, Tel: 0755- 86392243, E-mail: dong.liang@siat.ac.cn

文章历史

收稿日期：2019-03-15
在线发表日期：2019-05-30

Contents Abstract Full text Figures/Tables PDF

基于深度递归级联卷积神经网络的并行磁共振成像方法

程慧涛 ^1,2, 王珊珊 ³, 柯子文 ¹, 贾森 ³, 程静 ³, 丘志浪 ³, 郑海荣 ³, 梁栋 ^1,2

1. 医学人工智能研究中心(中国科学院深圳先进技术研究院), 广东深圳 518055;
2. 中国科学院大学, 北京 100049;
3. 保罗C. 劳特伯生物医学成像研究中心(中国科学院深圳先进技术研究院), 广东深圳 518055

收稿日期：2019-03-15; 在线发表日期：2019-05-30

基金项目：国家重点研发计划（2017YFC0108802）

通讯联系人(Corresponding author)：梁栋, Tel: 0755- 86392243, E-mail: dong.liang@siat.ac.cn

摘要: 快速磁共振成像是磁共振研究领域重要的课题之一.随着大数据和深度学习的兴起，神经网络成为快速磁共振技术的重要方法.然而网络性能表现和网络参数量之间较难取得平衡，且对于多通道数据重建的并行成像问题，相关研究较少.本文构建了一种深度递归级联卷积神经网络结构，用于处理并行成像问题.这种网络结构在减少网络参数量的同时，能够尽可能地提高网络的表达能力，提高网络重建的精确度.实验结果表明，相较于传统并行成像方法，通过训练好的神经网络对欠采样磁共振数据进行重建，可以得到更准确的重建结果，且重建时间大大缩短.

关键词: 快速磁共振成像并行成像深度学习卷积神经网络先验信息

A Deep Recursive Cascaded Convolutional Network for Parallel MRI

CHENG Hui-tao ^1,2, WANG Shan-shan ³, KE Zi-wen ¹, JIA Sen ³, CHENG Jing ³, QIU Zhi-lang ³, ZHENG Hai-rong ³, LIANG Dong ^1,2

1. Research Center for Medical AI(Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences), Shenzhen 518055, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Paul C. Lauterbur Research Center for Biomedical Imaging(Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences), Shenzhen 518055, China

Abstract: Fast magnetic resonance imaging (MRI) has been attracting more and more research interests in recent years. With the emergence of big data and development of advanced deep learning algorithms, neural network has become a common and effective tool for image reconstruction in fast MRI. One main challenge to the deep learning-based methods for fast MRI reconstruction is the trade-off between the network performance and the network capacity. Few previous studies have used the deep learning-based methods in parallel imaging. In this work, a deep recursive cascaded convolutional network (DRCCN) architecture was designed for parallel MRI, with reduced number of network parameters while maintaining a satisfactory performance. The experimental results demonstrated that, compared to the classical methods, image reconstruction with the well-trained DRCCN networks were more accurate and less time consuming.

Key words: fast magnetic resonance imaging parallel imaging deep learning convolutional neural network prior knowledge

引言

磁共振成像（magnetic resonance imaging，MRI）技术是重要的医学影像技术手段，具有无创、无辐射、多对比度等特性.但磁共振数据的采集速度受限于物理（磁场强度等）和生理（神经刺激等）等方面的因素^[1]，扫描时间过长是制约MRI技术发展的主要障碍.为此许多研究专注于在保持良好图像质量的前提下，如何减少数据的采集量，从而达到加速磁共振扫描的目的.

并行成像（parallel imaging）技术可有效加快MRI扫描.该技术通过多个线圈同时接收信号来记录图像不同位置的敏感度信息，然后利用该敏感度信息进行加速扫描和图像重建.多个独立线圈采集得到的数据可以通过多种并行算法进行图像重建，其中典型的方法有GRAPPA^[2]、SENSE^[3]、SPIRiT^[4]等.基于压缩感知（compressed sensing，CS）理论的快速磁共振图像重建方法能够在保证图像重建质量的情况下，突破奈奎斯特采样定律，通过较低的采样率达到减少扫描时间的目的.CS-MRI方法主要通过小波变换（wavelet）^[5]、全变分（total variation，TV）^[6]、字典学习（dictionary learning）^{[7, 8]}等利用图像稀疏性作为先验信息进行图像重建.尽管CS-MRI有望在临床环境中得到有效应用^[9]，但是目前大多数的临床MRI扫描仪仍然是基于全采样序列或者仅使用并行成像技术来加速.其中主要的原因在于：（1）CS-MRI要求非相干性欠采样^[10]；（2）广泛使用的变换域过于简单，不能捕捉到与生物组织结构相关的图像细节.比如，基于TV的变换域惩罚重建图像中的局部差分，但会造成阶梯状伪影；（3）非线性的最优化算法通常涉及到耗时相对较长的迭代计算^[10]；（4）目前CS-MRI方法中不合适的参数选择可能会导致过正则化，从而造成图像模糊、不真实，或存在明显的伪影^[10].基于以上限制，目前CS-MRI的加速倍数仍然非常有限.

近几年，深度学习在计算机视觉领域得到了广泛的关注，并且取得了突出的成果.基于深度学习的快速MRI方法也取得了一定进展.作者所在团队在国际上首次提出了基于卷积神经网络的快速磁共振重建方法^[11].随后，深度学习在快速磁共振重建领域广泛应用开来.总的来说，这些方法可以分为两类：第一类是将传统算法进行网络化学习，如ADMM-Net^[12]、VN-net^{[13, 14]}等；第二类是利用神经网络进行端到端地学习，如DC-CNN^[15]、AUTOMAP^[16]、U-net^[17]等等.

本文搭建了一种递归级联卷积神经网络结构，用于多通道数据重建的并行成像.它能够在减少参数量的同时，尽可能地提高网络的拟合能力和表达能力，从而进一步降低网络训练的损失，提高网络重建的准确度.

1 理论与方法 1.1 卷积神经网络

卷积神经网络因其具有权值共享、局部连接等特性，在图像处理方面有独特的优势.一个L层的卷积神经网络$y = C(x, \theta )$可以表示为

$ \left\{ \begin{array}{l} {C_0} = X\\ {C_l} = {\sigma _l}({\mathit{\Omega }_l}*{C_{l - 1}} + {b_l})\;\;\;\;\;\;l = 1, 2, \cdots , L - 1\\ {C_L} = {\mathit{\Omega }_L}*{C_{L - 1}} + {b_L} \end{array} \right. $

(1)

C₀表示卷积神经网络的输入.${\mathit{\Omega }_l}$表示一个大小为$F{W_l} \times F{H_l} \times {K_{l - 1}} \times {K_l}$的卷积运算，$F{W_l} \times F{H_l}$为第l层的卷积核大小；K_l和K_l-1为第l层和(l-1)层的卷积核的数量，亦即第l层和(l-1)层特征图的数量.C_l和C_l-1为第l层和(l-1)层卷积神经网络的输出.${\sigma _l}$代表一种非线性映射操作.b_l是一个K_l维的向量偏置.${\mathit{\Omega }_L}$表示第L层卷积神经网络的卷积运算.整个卷积神经网络的输出y为C_L，即最后一层的输出.(1)式可看作是卷积神经网络训练阶段的前向过程，其中卷积操作用于提取图像特征，${\sigma _l}$用于进行非线性激活.

除前向传播之外，反向传播用于计算反向梯度，从而更新网络参数，是卷积神经网络训练阶段的重要过程.给定训练集$(x, y)$，反向传播就是更新参数$\{ ({\mathit{\Omega }_1}, {b_1}), \cdots , ({\mathit{\Omega }_l}, {b_l}), \cdots , ({\mathit{\Omega }_L}, {b_L})\} $，进而最小化损失函数

$ \hat \theta = \arg \mathop {\min }\limits_\theta J(x, y) $

(2)

其中$J(x, y)$是由特定任务决定的损失函数.一旦经过训练后获得$\hat \theta $，它便可以用于线上测试任务，即用于预测目标输出$y = C(x, \hat \theta )$，其中x为线上测试的输入.

1.2 递归网络结构

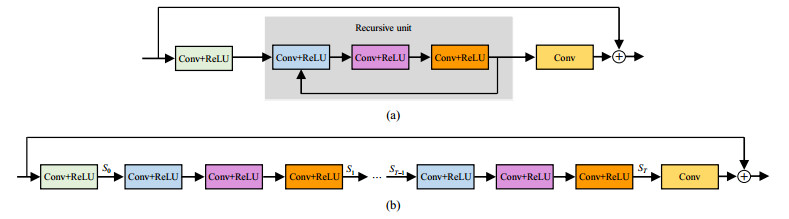
在神经网络中，网络参数量和网络表达能力之间的平衡是一个难题，而递归结构可很好的解决这个问题.图 1展示了本文所使用的一个包含递归结构的模块.一个递归结构包含多个卷积层和激活层，且在网络结构中重复使用T次.若将一个递归结构表示为映射函数$f( \cdot )$，则第t次到第$(t + 1)$次的递归表示为

$ {s_{t + 1}} = f({s_t}) $

(3)

图 1 包含递归结构的卷积神经网络单元(a)及其展开形式(b)，相同颜色的卷积层共享权重 Fig. 1 An illustration of a recursive CNN block (a) and its unfolded structure (b). The layers in same color share the weights

s_t表示第t次输入递归结构时的特征图.将重复T次的递归结构展开，其本质是多个网络层共享权值，因此在保持网络较好表达能力的同时，能够减少网络参数量.递归结构的重复使用次数T和每个递归结构包含的层数R可以根据具体任务进行调节，本文实验将T和R均设置为3.

1.3 本文提出的网络框架

本文提出了一种深度递归级联卷积神经网络（deep recursive cascaded convolutional network，DRCCN），用于学习从欠采样磁共振图像到全采样磁共振图像之间的映射关系.图 2展示了DRCCN网络结构.网络的输入为零填充欠采样K空间数据经傅里叶逆变换得到的12通道欠采样磁共振图像，输出为由全采样K空间数据重建得到的12通道磁共振图像.我们将复数磁共振数据的实部和虚部在通道维度上拼接在一起，输入到网络当中.整个网络由多个模块级联而成，每个模块包含一个递归的卷积神经网络单元（recursive CNN unit）和一个数据一致性（data consistency，DC）单元.每个递归的卷积神经网络单元是一个如图 1所示的残差结构.在级联的卷积神经网络单元之间，采集到的欠采样K空间数据用于更新每个卷积神经网络单元的输出，从而能够保证每个单元输出的数据一致性.每个卷积层的卷积核大小为3×3，每个CNN单元中，除最后一层的特征图数量为24外（其中前12个特征图为输出复数图像的实部，后12个特征图为其虚部），其余各层的输出均为64个特征图.除最后一层外，线性整流函数（rectified linear unit，ReLU）用在其余各层之后，进行非线性激活.值得注意的是，整个网络中模块数量n_b和每个CNN单元中实际卷积层个数n_c可以依据实际任务进行调整，我们的所有实验中n_b=10，n_c=5.

图 2 本文提出的网络结构图 Fig. 2 The architecture of the proposed network

训练过程中，网络中的参数由最小化损失函数进行计算梯度和更新.我们采用真实数据和网络输出之间的绝对值误差作为损失函数，即

$ J(x, y) = \frac{1}{M}\sum\limits_{m = 1}^M {||C({x_m};\theta ) - {y_m}||} $

(4)

其中，C表示神经网络的输出，x_m表示训练集中第m个输入（由零填充K空间数据变换得到的12通道欠采样图像），y_m是对应的全采样图像，M表示训练集中训练图像的数量，θ表示卷积神经网络中待学习的网络参数.

1.4 数据一致层

各个级联的CNN单元的输出可以逐步地接近于真实图像，但对于K空间已采集的位置来说，CNN单元的输出往往会失真.为了保证K空间已采集位置的数据一致性，我们在每个CNN单元后加入了数据一致层.具体地，令f_l表示网络输出图像的K空间，即${f_{l, j}} = {\mathbb{F}}{y_{l, j}} = {\mathbb{F}}{C_{l, j}}(x;\theta )$，${f_l}(k)$表示K空间在位置k处的值.为了确保数据一致性，CNN输出图像的K空间需要用已采集到的K空间数据进行更新

$ f_l^{rec}(k) = \left\{ \begin{array}{l} {f_l}(k)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;k \notin S\\ \frac{{{f_l}(k) + \lambda {f_0}(k)}}{{1 + \lambda }}\;\;\;\;\;\;{\rm{if}}\;\;k \in S \end{array} \right. $

(5)

其中f₀表示已采集到的K空间数据，S表示所有已采集的位置集合，λ为权重参数.我们将λ设为无穷大，即如果K空间相应的位置已采集，那么最终更新后的K空间将采用此采集到的K空间值.最后更新得到的K空间进行傅里叶反变换，便可以得到该模块输出的重建图像，进而可以输入到下一个模块进行进一步优化.

2 实验 2.1 数据集

我们利用Siemens MAGNETOM Trio 3T人体MRI扫描仪，采用12通道头部线圈采集了3 000多张二维全采样多通道磁共振K空间数据，包含了冠状面、矢状面和水平面的数据，且数据大小有256×256和270×256两种.对于270×256数据，我们在图像域去掉其部分背景信息，将其切成256×256大小的数据，以保证所有数据维度一致.数据采集过程中，我们采用的是快速自旋回波（turbo spin-echo，TSE）序列.

在数据预处理过程中，我们将采集到的多通道图像数据进行模值归一化，即所有像素值除以该图像的最大模值.归一化后的图像即为训练数据的标签.随后，对标签数据进行回顾式欠采样得到训练数据的输入.深度学习依赖于大数据，这对于医学图像来说并不易获得，因此数据增强（如刚体变换等）对于提高网络性能和防止过拟合起着很重要的作用.具体地，对每一幅图像依次旋转π/2、π和3π/2，以及沿x轴和y轴进行翻转，最终可以得到原始数据8倍量的图像数据.数据增强后，取10%的数据作为测试数据，剩余的数据按照9:1的比例分为训练数据和验证数据.

2.2 网络设置

本文实验进行网络训练时，每批数据量（batch size）为4，共进行40轮（epoch）训练.实验所使用的优化器（optimizer）为Adam方法，其中参数设置为β₁=0.9，β₂=0.999，初始学习率l_r= 0.000 1.实验设备为一台配备Quadro K40c显卡、128G内存、Intel Xeon(R) CPU E5-2660 v3、Ubuntu 14.04 LTS（64位）系统的工作站.整个训练在Tensorflow框架下完成.测试阶段既可以在Matlab 2015b平台中完成，也可以在Tensorflow框架下完成.

2.3 欠采样方式

我们的实验采用了3种不同类型的欠采样模式，包括一维变密度随机采样、一维均匀采样和二维泊松变密度采样.对于二维泊松变密度采样，我们通过保留20%和10%的K空间数据来模拟5倍和10倍加速.而对于一维随机和均匀采样，我们模拟了3倍和4倍加速.值得注意的是，对于每一种采样模式都需要训练不同的模型，而对于特定任务的训练，采样模式是固定的.

3 实验结果 3.1 与传统并行成像方法的对比

为验证本文提出DRCCN方法的有效性，我们将该方法与SPIRiT和L1-SPIRiT两种具有代表性的快速成像方法在多种采样方式和采样率下进行了对比.在一维随机和均匀欠采样方式下，SPIRiT和L1-SPIRiT都采用了典型的参数设置：核大小为5×5，校正区域为中心24条线.对于SPIRiT，迭代次数设为30.而对于基于CS的并行成像方法L1-SPIRiT，Tikhonov正则化参数设为0.01，小波软阈值正则化参数设置为0.001 5.峰值信噪比（peak signal to noise ratio，PSNR）和结构相似性（structural similarity，SSIM）用于评估图像质量.

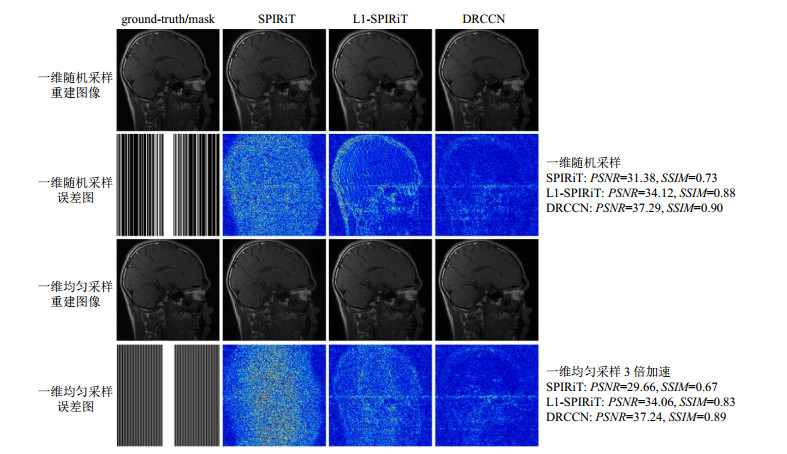
图 3展示了在一维随机采样和一维均匀采样3倍加速下使用SPIRiT、L1-SPIRiT和本文提出的DRCCN方法得到的重建结果.值得注意的是，这里所说的3倍在计算时包含了中心校正线.可以看到，DRCCN的重建结果更接近于真实图像，而SPIRiT和L1-SPIRiT的重建结果有肉眼可见的混叠伪影和噪声.从对应的误差图上也可以得到同样的结论.

图 3 一维随机采样和一维均匀采样3倍加速时，使用SPIRiT、L1-SPIRiT和DRCCN的重建结果和误差图 Fig. 3 The reconstruction and error maps using SPIRiT, L1-SPIRiT and DRCCN methods under 1D random and 1D uniform sampling at a net acceleration factor of 3

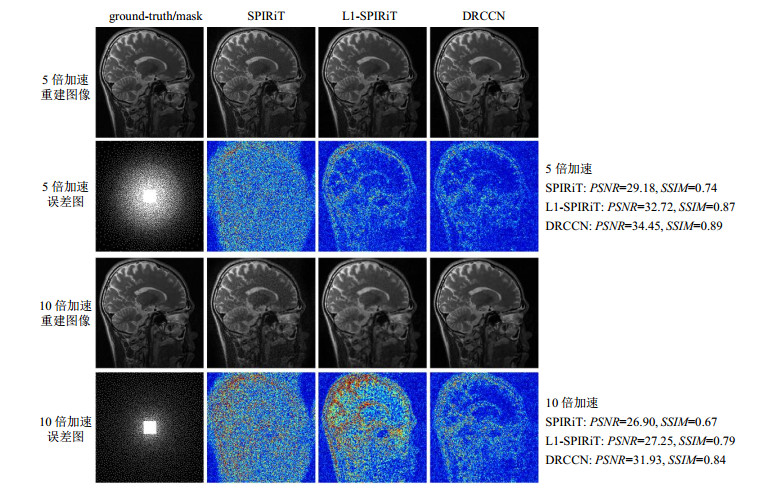
为了进一步验证DRCCN方法的有效性，我们还在二维泊松变密度采样模式下进行了对比实验，如图 4所示.对于5倍和10倍加速，SPIRiT和L1-SPIRiT的校正区域均为30×30，重建迭代次数均为30次.可以较为明显地观察到，无论是5倍还是10倍加速，DRCCN方法的重建结果都优于SPIRiT和L1-SPIRiT.

图 4 二维泊松变密度采样5倍和10倍加速时，使用SPIRiT、L1-SPIRiT和DRCCN的重建结果和误差图 Fig. 4 The reconstruction and error maps using SPIRiT, L1-SPIRiT and DRCCN methods under 2D Poisson disc sampling at net acceleration factors of 5 and 10

3.2 对校正线的敏感度

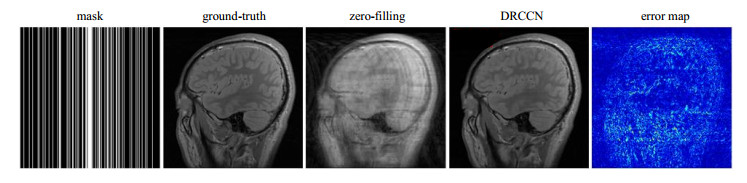
传统的并行成像方法，如GRAPPA、SPIRiT和L1-SPIRiT，都对采样模式中心自动校正信号（auto-calibration signal，ACS）有一定的要求，即K空间中心区域必须有一部分全采样，且该中心校正区域的大小对其重建结果有这较大影响.当中心校正区域过小时，这些方法的重建结果往往很差.而本文提出的DRCCN并行成像方法对中心校正区域的大小并不敏感.图 5展示了在一维随机欠采样模式、4倍加速下，中心校正线（ACS line）只有8条时，DRCCN的重建结果.可以看到，即使ACS线很少，DRCCN仍然能够得到较为满意的重建效果.

图 5 一维随机欠采样模式、4倍加速、中心校正线为8条时，使用DRCCN的重建结果及误差图.PSNR=36.60，SSIM=0.92 Fig. 5 The reconstruction of DRCCN under 1D random undersampling at a net acceleration factors of 4 with 8 ACS lines. PSNR=36.60, SSIM=0.92

3.3 收敛性分析

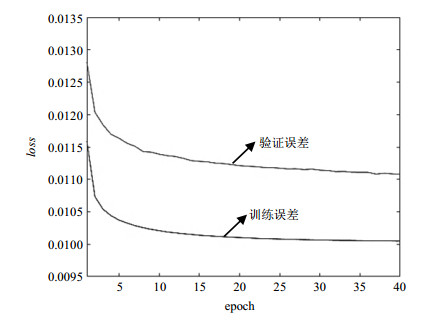
对于深度学习来说，模型训练是否存在欠拟合或者过拟合是必须要考虑的一个问题.模型训练的误差下降曲线可以较好地反映这一问题是否存在.图 6展示了我们对DRCCN模型进行训练时的误差随迭代次数（epoch）的下降曲线.可以看到，随着epoch数的增加，训练误差和验证误差均逐渐趋于收敛，且验证误差略高于训练误差.这说明模型训练相对合理.

图 6 模型的训练误差和验证误差的下降曲线.纵坐标loss表示损失函数（绝对值误差） Fig. 6 The loss curves of training and validation. Y-axis represents the value of loss function (mean absolute error)

3.4 重建时间分析

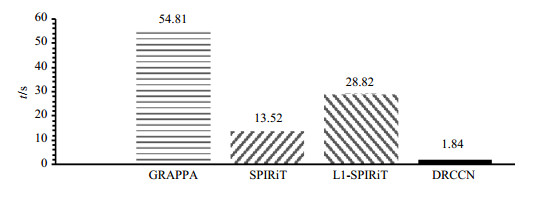
重建时间也是重建算法必须要考虑的一个问题.在我们的实验中，有两种测试方法可以用于重建多通道图像.一种方法是在Tensorflow框架下进行网络的前向过程，且支持GPU加速，另一种方法在Matlab平台下计算网络前向过程.如果采用第一种方法，且网络具体参数设置和我们的实验一样，DRCCN的重建时间大约是2.0 s，远远快于传统的并行成像算法，这得益于计算图和GPU加速的优势.而如果采用第二种方法，DRCCN的重建时间大约为100 s.因此，我们建议线上测试过程在基于计算图和GPU加速的Tensorflow平台下进行.图 7展示了DRCCN和传统并行成像算法的重建时间对比.

图 7 DRCCN与传统并行成像方法的重建时间对比 Fig. 7 Comparison of the reconstruction time using DRCCN and classical parallel imaging methods

4 结论

本文提出了一种用于多通道并行成像的深度递归级联的卷积神经网络模型——DRCCN，相比于传统的并行成像方法，它能够得到更准确的重建结果，且重建时间大大缩短.但是DRCCN方法仍然有一些限制和需要改进的地方.对于不同的采样方式和不同的采样率，DRCCN必须重新进行训练，这可能会耗费相当长的线下训练时间.同时，对数据集的依赖性较高.除了数据集大小之外，对于和训练集不同部位的数据进行重建，DRCCN的泛化能力仍有待考究.

参考文献

[1]	LUSTIG M, DONOHO D L, SANTOS J M, et al. CompressedSensing MRI[J]. IEEE Signal Proc Mag, 2008, 25(2): 72-82. DOI: 10.1109/MSP.2007.914728.
[2]	GRISWOLD M A, JAKOB P M, HEIDEMANN R M, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA)[J]. Magn Reson Med, 2002, 47(6): 1202-1210. DOI: 10.1002/mrm.10171.
[3]	PRUESSMANN K P, WEIGER M, SCHEIDEGGER M B, et al. SENSE:sensitivity encoding for fast MRI[J]. Magn Reson Med, 1999, 42(5): 952-962. DOI: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S.
[4]	LUSTIG M, PAULY J M. SPIRiT:iterative self-consistent parallel imaging reconstruction from arbitrary k-space[J]. Magn Reson Med, 2010, 64(2): 457-471.
[5]	CHAI Q H, SU G Q, NIE S D. Compressive sensing low-field MRI reconstruction with dual-tree wavelet transform and wavelet tree sparsity[J]. Chinese J Magn Reson, 2018, 35(4): 486-497. 柴青焕, 苏冠群, 聂生东. 双树小波变换与小波树稀疏联合的低场CS-MRI算法[J]. 波谱学杂志, 2018, 35(4): 486-497.
[6]	LIANG D, WANG H F, CHANG Y C, et al. Sensitivity encoding reconstruction with nonlocal total variation regularization[J]. Magn Reson Med, 2011, 65(5): 1384-1392. DOI: 10.1002/mrm.22736.
[7]	LIU Q G, WANG S S, YING L, et al. Adaptive dictionary learning in sparse gradient domain for image recovery[J]. IEEE T Image Process, 2013, 22(12): 4652-4663. DOI: 10.1109/TIP.2013.2277798.
[8]	SONG Y, XIE H B, YANG G. Dictionary learning with segmentation for compressed-sensing magnetic resonance imaging[J]. Chinese J Magn Reson, 2016, 33(4): 559-569. 宋阳, 谢海滨, 杨光. 用于压缩感知磁共振成像的分割字典学习算法[J]. 波谱学杂志, 2016, 33(4): 559-569.
[9]	JASPAN O N, FLEYSHER R, LIPTON M L. Compressed sensing MRI:a review of the clinical literature[J]. Br J Radiol, 2015, 88(1056): 20150487. DOI: 10.1259/bjr.20150487.
[10]	HOLLINGSWORTH K G. Reducing acquisition time in clinical MRI by data undersampling and compressed sensing reconstruction[J]. Phys Med Biol, 2015, 60(21): R297. DOI: 10.1088/0031-9155/60/21/R297.
[11]	WANG S S, SU Z H, YING L, et al. Accelerating magnetic resonance imaging via deep learning[C]//IEEE: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), 2016: 514-517.
[12]	YANG Y, SUN J, LI H B, et al. Deep ADMM-Net for compressive sensing MRI[C]//LEE D D, SUGIYAMA M, LUXBURG U V, et al. Advances in neural information processing systems 29, 2016: 10-18.
[13]	HAMMERNIK K, KLATZER T, KOBLER E, et al. Learning a variational network for reconstruction of accelerated MRI data[J]. Magn Reson Med, 2018, 79(6): 3055-3071. DOI: 10.1002/mrm.26977.
[14]	KNOLL F, HAMMERNIK K, KOBLER E, et al. Assessment of the generalization of learned image reconstruction and the potential for transfer learning[J]. Magn Reson Med, 2019, 81(1): 116-128. DOI: 10.1002/mrm.27355.
[15]	SCHLEMPER J, CABALLERO J, HAJNAL J V, et al. A deep cascade of convolutional neural networks for dynamic MR image reconstruction[J]. IEEE T Med Imaging, 2018, 37(2): 491-503. DOI: 10.1109/TMI.2017.2760978.
[16]	ZHU B, LIU J Z, CAULEY S F, et al. Image reconstruction by domain-transform manifold learning[J]. Nature, 2018, 555(7697): 487-492. DOI: 10.1038/nature25988.
[17]	HAN Y, YOO J, KIM H H, et al. Deep learning with domain adaptation for accelerated projection-reconstruction MR[J]. Magn Reson Med, 2018, 80(3): 1189-1205. DOI: 10.1002/mrm.27106.