2. 北京交通大学 理学院, 北京 100044
2. School of Science, Beijing Jiaotong University, Beijing 100044, China
极化3He已被广泛应用于众多研究领域.它可以作为中子自旋过滤器(NSF)极化中子[1-3],可用于自旋相关的新物理探测[4, 5]和磁共振成像(MRI)等[1].国内外的许多中子源都开展了极化3He的研究项目[3, 6-11].据了解,中国绵阳研究堆(CMRR)已经建立国内首个用于中子极化的自旋交换光学泵浦(SEOP)极化3He系统,3He的最高极化率达72.7%±0.4%[6].在极化3He实验中,可以通过优化主磁场的梯度和窄化激光频率提高极化率[7, 12].核磁共振(NMR)和电子顺磁共振(EPR)是两种常用的分别测量3He相对极化率和真实极化率的技术[1, 13-15].依据这两种技术,3He极化率测量系统可以分为三个子系统(图 1),包括用于测量3He相对极化率的自由感应衰减(FID)NMR系统、用于翻转3He核自旋极化方向的绝热快速过程(AFP)NMR系统和用于测量3He真实极化率的EPR系统.
|
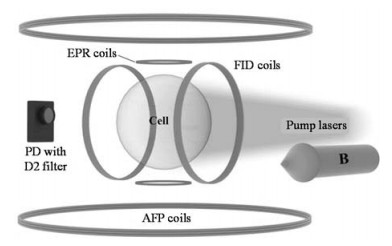
图 1 3He极化率测量系统结构示意图. PD:光电二极管;D2:铷原子D2谱线 Fig. 1 Diagram of the 3He polarimetry system. PD: Photo-diode; D2: Rb D2 line |
在实际应用中,因为FID信号的强弱与线圈大小、线圈匝数、线圈与3He气室的距离,以及3He磁化矢量偏转的角度和均匀度等多个因素有关,而且这些因素通常无法被准确测量,所以仅通过FID信号很难准确测定3He的真实极化率,只能监测3He极化率的相对变化情况.但值得注意的是,基于FID的测量只需要3He磁化矢量发生微小的偏转,不会造成3He极化率的很大损失,因此是一种最为方便的3He相对极化率测量方法.在极化3He实验中,还可以通过对比AFP自旋翻转前后FID信号的幅值和相位信息,来判断3He的核自旋是否完全翻转以及真实极化率的损失情况.
本文主要设计和实现了FID NMR系统;并基于虚拟仪器的概念[16, 17],利用Matlab实现了3He相对极化率的定时检测;优化了拾波线圈(FID线圈)的构形和参数;并对系统的噪声进行了测量.
1 FID NMR测量系统 1.1 测量原理3He原子的核自旋不为0,具有核磁矩.当其位于恒定磁场中时,核磁矩在一定时间内沿磁场方向排列,在宏观上形成原子核的磁化强度.根据NMR原理,如果对此时的3He系统发射一段共振频率
|
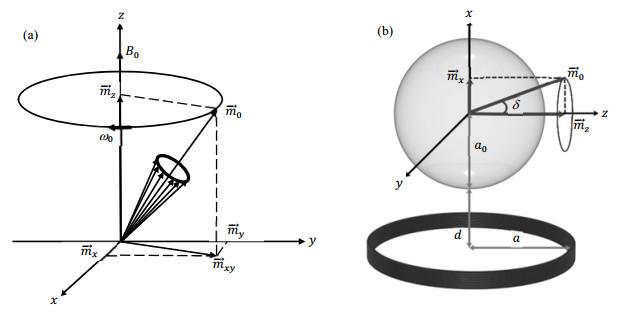
图 2 (a) 3He磁化矢量的进动;(b)球形3He气室和拾波线圈的示意图 Fig. 2 (a) Precession of 3He magnetization vector; (b) Schematic diagram of spherical 3He cell and pickup coil |
假设恒定磁场沿着z轴正方向,则旋进过程中3He磁化矢量在x轴的分量为[6, 8, 15]:
| $ {m_x} = m \cdot \sin \delta \cdot \sin ({\omega _0}t + \phi ){{\rm{e}}^{ - t/{T_2}}} $ | (1) |
式中
以球形玻璃气室为例,在射频脉冲过后,放置于气室旁的匝数为n、平均半径为a的拾波线圈的感应电动势ε为[8, 18-20]:
| $ \varepsilon \approx - \frac{{2{\rm{ \mathsf{ π} }}{\mu _0}a_0^3}}{3} \cdot \frac{{n{a^2}}}{{{{[{a^2} + {{({a_0} + d)}^2}]}^{3/2}}}} \cdot {m_0} \cdot {\omega _0} \cdot \sin \delta \cdot \cos ({\omega _0}t + \phi ){{\rm{e}}^{ - t/{T_2}}} $ | (2) |
式中
文献[8]介绍了一种优化拾波线圈的方法,但文中所参考的电感计算公式只适用于长螺线管(长度 > > 半径)[22-25],并不符合实际情况.所以本文将对其电感计算公式进行修正,进而对拾波线圈的构形和参数进行优化.根据文献[8]的结论,FID信号的信噪比(SNR)为:
| $ SNR = \frac{\varepsilon }{{\sqrt {|N{|^2}\Delta f} }} \approx \frac{\varepsilon }{{|{N_E}|}} \cdot \sqrt {\frac{{2{\rm{ \mathsf{ π} }}L}}{R}} $ | (3) |
其中,Δf是谐振电路的带宽,
|
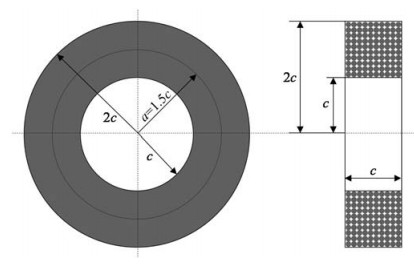
图 3 Brooks线圈及其截面示意图 Fig. 3 Diagram of Brooks coil and its cross section |
| $ L = 1.6994 \times {10^{ - 6}} \times a{n^2} $ | (4) |
结合(2)式和(3)式,可得拾波线圈的信噪比:
| $ SNR \propto - \frac{{0.01687a_0^3}}{{\sqrt P }} \cdot \frac{{\sqrt {ns} }}{{\sqrt \rho {{[{a^2} + {{({a_0} + d)}^2}]}^{3/2}}}} \cdot {m_0} \cdot {\omega _0} \cdot \sin \delta \cdot \cos ({\omega _0}t + \phi ){{\rm{e}}^{ - t/{T_2}}} $ | (5) |
上式中第一项仅与3He气室的半径、电磁辐射的平均功率密度相关;第三项仅与极化3He气体的特性相关.对于一个给定的极化3He系统而言,第一项和第三项涉及的参数往往都是确定的,仅第二项中与线圈相关的参数可以优化.令第二项为
| $ F = \frac{2}{3}\sqrt {\frac{\beta }{\rho } \cdot } \frac{a}{{{{[{a^2} + {{({a_0} + d)}^2}]}^{3/2}}}} $ | (6) |
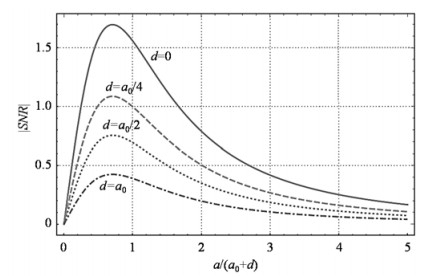
可见,F与线圈的平均半径、间距系数、导线的电阻率、拾波线圈与气室的距离有关,而与线圈的匝数和导线的截面积无关,因为它们可以通过线圈的平均半径和间距系数定义.从F因子中不难得出线圈的间距系数越大,或导线的电阻率越小,|SNR|越高.a/(a0+d)与|SNR|的关系如图 4所示:|SNR|随着平均半径的增加先逐渐增大后逐渐减小,当
|
图 4 |SNR|与a/(a0+d)的关系 Fig. 4 The relationship between |SNR| and a/(a0+d) |
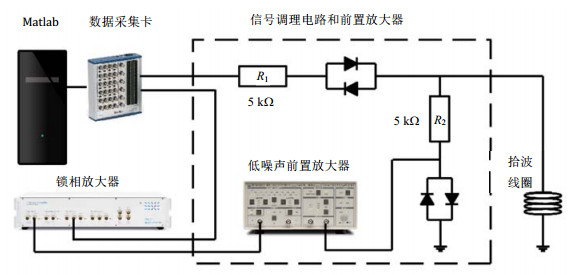
FID NMR系统的电路图如图 5所示,整个系统由Matlab程序控制.具体过程为:首先由Matlab与数据采集(DAQ)卡生成一个射频脉冲,通过信号调理电路发送到拾波线圈,脉冲过后,3He原子产生的进动信号由同一线圈拾取,线圈内产生的感应电压信号首先输入低噪声的前置放大器(SRS-RS560),依次通过其内部最大带宽为DC-1MHz的滤波器和最大增益达50 000倍的放大器,经过滤波和放大的信号再输入锁相放大器(HF2LI),通常设定锁相放大器的参考频率
|
图 5 FID NMR系统电路图 Fig. 5 Circuit diagram of FID NMR system |
实验装置如图 6所示,采用Merrit构形的方形四线圈提供恒定磁场,其中心区域的场强约为16×10-4 T,对应的3He核的拉莫尔进动频率约为52 kHz,信号调理电路固定在电路盒中,拾波线圈安装在加热腔之内,左右两个线圈对称放置,与恒定磁场方向垂直,其平均半径为5.2 cm,采用电导率为1.75×10−8 Ω·m、直径为100 µm的铜导线各缠绕440匝,测得其总阻值为614.4 Ω(理论计算值为616 Ω).

|
图 6 FID NMR系统实物图 Fig. 6 The designed FID NMR system |
Matlab最终接收到的信号如图 7所示,图 7(a)是单次测量的数据,FID信号的幅值为0.1 V,频率为210 Hz,T2为24 ms,X(t)呈指数型衰减.图 7(b)是多次测量后得到的FID信号的幅值随光泵抽运时间的变化情况,0点是系统调试稳定后,启动FID NMR测量程序后的第一个测量点,测量间隔为1 h.3He的极化率与信号的幅值呈正比,呈现类指数型的增长,增幅随光学泵浦时间的增加而越来越小.

|
图 7 (a) FID信号;(b) FID信号的幅值与光泵抽运时间的关系 Fig. 7 (a) FID signals; (b) Relationship between FID signal amplitude and optical pumping time |
通常,极化3He实验是在5×10-4~30×10-4 T的低场强环境中进行的[1, 15, 29, 30],对应的3He的NMR频率大约为16.2~97.2 kHz.考虑到系统中SRS-RS560前置放大器的可选带宽以及滤波器的滚降特性,所以对10~100 kHz频率范围内的噪声进行了测量.测量电路如图 8所示,拾波线圈内的信号经过RS560的滤波和放大后直接输入到DAQ卡,由Matlab进行后续的数据分析[31].

|
图 8 拾波线圈噪声测量电路 Fig. 8 Circuit for noise measurement of pickup coil |
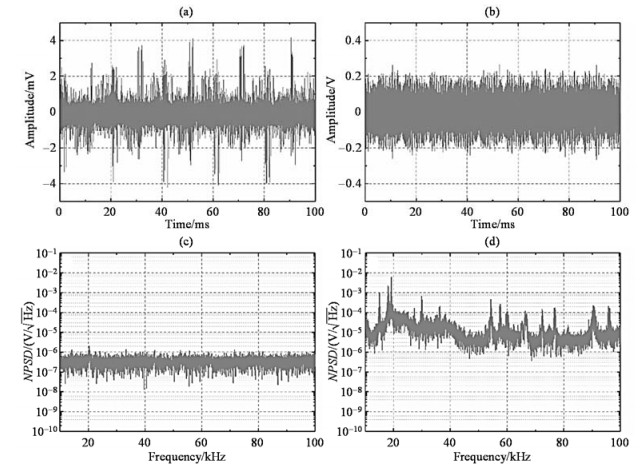
在3He被极化的过程中,3He气室和拾波线圈是暴露在实验室环境中的,作为对照,此次噪声的测量也同样将整个系统暴露在实验室环境中.因此测量的噪声主要为电阻热噪声、环境噪声、前置放大器噪声,以及DAQ卡噪声.已知前置放大器SRS-RS560的等效噪声功率谱密度为
本文设计并实现了FID NMR系统,成功检测到了极化3He磁化矢量的旋进信号,利用Matlab实现了对3He相对极化率的定时检测,结果表明泵浦过程中3He的极化率呈类指数型增长.通过对拾波线圈SNR的理论分析,发现采用Brooks构形的线圈有助于提高SNR,当线圈的平均半径为
|
图 9 系统噪声功率谱密度测量值. NPSD:噪声功率谱密度 Fig. 9 Measurement of noise power spectral density of the system. NPSD: noise power spectral density |
| [1] | GENTILE T R, NACHER P J, SAAM B, et al. Optically polarized 3He[J]. Rev Mod Phys, 2017, 89(4): 045004. DOI: 10.1103/RevModPhys.89.045004. |
| [2] | CHEN W C, GENTILE T R, YE Q, et al. Recent advancements of wide-angle polarization analysis with 3He neutron spin filters[J]. Journal of Physics:Conference Series, 2016, 746(1): 012016. |
| [3] | BABCOCK E, SALHI Z, GAINOV R, et al. Recent on-beam tests of wide-angle neutron polarization analysis with a 3He spin filter:magic pastis on V20 at HZB[J]. Journal of Physics:Conference Series, 2017, 862(1): 012002. |
| [4] | FU C B, GENTILE T R, SNOW W M. Limits on possible new nucleon monopole-dipole interactions from the spin relaxation rate of polarized 3He gas[J]. Phys Rev D, 2011, 83(3): 031504. DOI: 10.1103/PhysRevD.83.031504. |
| [5] | YAN H, SUN G A, PENG S M, et al. Searching for new spin-and velocity-dependent interactions by spin relaxation of polarized 3He gas[J]. Phys Rev Lett, 2015, 115(18): 182001. DOI: 10.1103/PhysRevLett.115.182001. |
| [6] | YAN S, ZHANG M F, GUO W C, et al. Development of a polarized 3He neutron spin filter based on spin exchange optical pumping at china mianyang research reactor[J]. Sci China Phys Mech Astron, 2019, 62: 102021. DOI: 10.1007/s11433-019-9410-3. |
| [7] |
WANG W Z, HU B T, ZHENG H, et al. A new magnetic field system for 3He polarization[J].
Acta Phys Sin, 2018, 67(17): 176701.
王文钊, 胡碧涛, 郑皓, 等. 一种可用于极化3he实验的新型磁场系统[J]. 物理学报, 2018, 67(17): 176701. DOI: 10.7498/aps.67.20180571. |
| [8] | TU X Q, ZHENG H, SUN G A, et al. Pickup coil optimization for polarized 3He system[J]. The European Physical Journal Plus, 2017, 132(7): 308-318. DOI: 10.1140/epjp/i2017-11580-y. |
| [9] | SUN G A, ZHANG C S, CHEN B, et al. A new operating neutron scattering facility CMRR in china[J]. Neutron News, 2016, 27(4): 21-26. DOI: 10.1080/10448632.2016.1233018. |
| [10] | LIU Y T, CHEN D F. Overview and progress of neutron scattering facilities at CARR[J]. Aapps Bulletin, 2014, 24(2): 20-22. |
| [11] | CHEN H S, WANG X L. China's first pulsed neutron source[J]. Nat Mater, 2016, 15(7): 689-691. DOI: 10.1038/nmat4655. |
| [12] | CHEN W C, GENTILE T R, YE Q, et al. On the limits of spin-exchange optical pumping of 3He[J]. J Appl Phys, 2014, 116(1): 014903. DOI: 10.1063/1.4886583. |
| [13] | LEE S, MOON M K, KIM J, et al. In-situ compact 3He neutron spin polarizer based on a magneto-static cavity with built-in NMR coils[J]. Journal of Physics:Conference Series, 2016, 711(1): 012014. |
| [14] | JIANG C Y, TONG X, BROWN D R, et al. New generation high performance in situ polarized 3He system for time-of-flight beam at spallation sources[J]. Rev Sci Instrum, 2017, 88(2): 025111. DOI: 10.1063/1.4975991. |
| [15] | BABCOCK E. Spin exchange optical pumping with alkali metal vapors[D]. Madison: University of Wisconsin Madison, 2005. |
| [16] |
LIU Y, SONG M H, WANG K, et al. A magnetic resonance receiver system design based on all programmable system-on-a-chip and LabVIEW[J].
Chinese J Magn Reson, 2018, 35(4): 475-485.
刘颖, 宋明辉, 王坤, 等. 基于全可编程SoC和LabVIEW的磁共振接收系统设计[J]. 波谱学杂志, 2018, 35(4): 475-485. |
| [17] |
GUO X Y, XIAO L. Design of a receiver for magnetic resonance imaging based on data acquisition card and GPU[J].
Chinese J Magn Reson, 2016, 33(4): 581-589.
郭新宇, 肖亮. 基于数据采集卡和GPU的MRI信号接收设计[J]. 波谱学杂志, 2016, 33(4): 581-589. |
| [18] | JACKSON J D. Classical Electrodynamics[M]. Wiley, 1998. |
| [19] | WILMS E, EBERT M, HEIL W, et al. Polarimetry on dense samples of spin-polarized 3He by magneto static detection[J]. Nucl Instrum Meth A, 1997, 2(401): 491-498. |
| [20] | ASAF G, MICHAEL J H, SUBHAS C M. High sensitivity magnetometers[M]. Springer, 2017. |
| [21] |
CHANG X, SU G Q, NIE S D. Wavelet transform-based signal denoising in low-field NMR[J].
Chinese J Magn Reson, 2018, 35(3): 393-406.
常晓, 苏冠群, 聂生东. 基于小波变换的低场核磁共振信号去噪方法的研究进展[J]. 波谱学杂志, 2018, 35(3): 393-406. |
| [22] | 卡兰塔罗夫(苏), 采依特林(苏). 电感计算手册[M]. 北京: 机械工业出版社, 1992. |
| [23] | GROVER F W. Inductance calculations-working formulas and tables[M]. New York: Dover Publication, 2009: 60-174. |
| [24] | ROSA E B. Formulae and tables for the calculation of mutual and self-inductance[M]. London: Forgotten Books, 2017: 45-60. |
| [25] | WHEELER H A. Inductance formulas for circular and square coils[J]. Proceedings of the IEEE, 1982, 70(12): 1449-1450. DOI: 10.1109/PROC.1982.12504. |
| [26] |
TIAN B F, WANG Y, ZHANG J, et al. Design and implementation of an electromagnetic noise set system in nuclear magnetic resonance sounding environment[J].
Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 2034-2042.
田宝凤, 王悦, 张健, 等. 核磁共振测深环境电磁噪声测试系统的设计及实现[J]. 吉林大学学报(工学版), 2015, 45(6): 2034-2042. |
| [27] |
XU P J. Measurement of electromagnetic radiation[J].
Nuclear Electronics & Detection Technology, 1986, S1(S1): 57-70.
徐培基. 电磁辐射的测量[J]. 核电子学与探测技术, 1986, S1(S1): 57-70. |
| [28] | 帅震清. 电磁环境测量技术[M]. 北京: 人民交通出版社, 2014. |
| [29] | MCKETTERICK T J, BOAG S, STEWART J R, et al. Optimized adiabatic fast passage spin flipping for 3He neutron spin filters[J]. Physica B, 2011, 406(12): 2436-2438. DOI: 10.1016/j.physb.2010.11.088. |
| [30] | CHANN B, BABCOCK E, ANDERSON L W, et al. Measurements of 3He spin-exchange rates[J]. Phys Rev A, 2002, 66(3): 032703. DOI: 10.1103/PhysRevA.66.032703. |
| [31] | WILLIAM H P, TEUKOLSKY S A, VETTERLING W T, et al. Numerical recipes:The art of scientific computing[M]. 3rd Ed. Cambridge: Cambridge University Press, 2007: 600-650. |
| [32] | HOROWITZ P, HILL W. The Art of Electronics[M]. Cambridge: Cambridge University Press, 1980: 520-560. |
| [33] | SHI H Y, WANG Y Z, LIN J. Optimal design of low-noise induction magnetometer in 1mHz-10kHz utilizing paralleled dual-JFET differential pre-amplifier[J]. IEEE Sensors Journal, 2016, 16(10): 3580-3586. DOI: 10.1109/JSEN.2016.2537928. |
| [34] | ART KAY. Operational amplifier noise:techniques and tips for analyzing and reducing noise[M]. Netherlands: Newnes, 2012. |
| [35] | ASPARUHOVA K K, GADJEVA E D. Noise analysis of operational amplifier circuits using MATLAB[C]. Banyak: 27th International Spring Seminar on Electronics Technology: Meeting the Challenges of Electronics Technology Progress, 2004. |
 2020, Vol. 37
2020, Vol. 37 
