小型化氢脉泽原子储存时间设计

引用本文 [复制中英文]

何克亮, 张为群, 林传富. 小型化氢脉泽原子储存时间设计[J]. 波谱学杂志, 2020, 37(2): 200-208. DOI: 10.11938/cjmr20192712.

HE Ke-liang, ZHANG Wei-qun, Lin Chuan-fu. Design of the Atomic Storage Time of a Miniaturized Hydrogen Maser[J]. Chinese Journal of Magnetic Resonance, 2020, 37(2): 200-208. DOI: 10.11938/cjmr20192712.

[复制英文]

通讯联系人

张为群, Tel:13585738245, E-mail:wqzhang@shao.ac.cn

文章历史

收稿日期：2019-02-02
在线发表日期：2019-05-30

Contents Abstract Full text Figures/Tables PDF

小型化氢脉泽原子储存时间设计

何克亮 ^1,2, 张为群 ¹, 林传富 ¹

1. 中国科学院上海天文台, 上海 200030;
2. 中国科学院大学, 北京 100049

收稿日期：2019-02-02; 在线发表日期：2019-05-30

通讯联系人(Corresponding author)：张为群, Tel:13585738245, E-mail:wqzhang@shao.ac.cn

摘要: 氢微波激射器（氢脉泽）采用原子储存泡对氢原子进行囚禁，在低损耗谐振腔内形成稳定的自持振荡.本文采用具备低腔频温度系数的介质加载谐振腔替换传统的腔-泡结构，实现了氢脉泽的小型化；并分析了这种小型化方案对频率稳定度和准确度的影响.原子储存时间设计值为0.4 s，闭环后的频率稳定度为5.6×10^-15/（1 000 s），与储存时间设计结果相吻合.

关键词: 氢脉泽原子储存时间弛豫时间频率稳定度

Design of the Atomic Storage Time of a Miniaturized Hydrogen Maser

HE Ke-liang ^1,2, ZHANG Wei-qun ¹, Lin Chuan-fu ¹

1. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China

Abstract: A hydrogen maser confines hydrogen atoms in the storage bulb and produces self-sustained oscillation in a low-loss resonance cavity. In this work, a miniaturized hydrogen maser was designed and fabricated utilizing a dielectric loaded cavity having a low frequency-temperature coefficient. The frequency stability and accuracy of the hydrogen maser were analyzed. The experimentally measured atomic storage time of the hydrogen maser was 0.4 s, and the frequency stability 5.6×10^-15/(1 000 s), agreeing with the design.

Key words: hydrogen maser atomic storage time relaxation time frequency stability

引言

氢微波激射器（氢脉泽）^[1]能够产生频率稳定且连续的相干微波信号，是主动型氢原子钟（氢钟）的物理部分.氢脉泽设计理论已较成熟，近二十年来，国内外对其研究的方向主要集中在如何提高技术水平^[2-7]和实现小型化.国外主动型氢钟的稳定度已可优于5×10^-16/d，而国内相应指标与国外相差1~3倍，在可靠性方面也与国外有一定差距.氢钟被广泛应用于导航、守时、甚长基线干涉测量和相对论理论的验证中^[8-11].将氢钟小型化会使其应用更加便捷，特别是在空间应用中.

腔-泡结构是氢脉泽的核心.原子储存泡位于谐振腔内部，储存泡中的氢原子与谐振腔TE₀₁₁模的轴向磁场相互作用，形成稳定的自持振荡.腔-泡体积是决定氢脉泽体积的主要因素之一，利用介质加载谐振腔可使腔-泡结构小型化，再配上相应的磁屏蔽和温控等外围结构，即可得到小型化氢脉泽.但当原子储存泡变小时，若不根据储存泡的体积重新设计原子储存时间和选择合适的原子束流，储存泡内的自旋交换碰撞弛豫会因氢原子密度增大而大幅变大，从而恶化氢钟指标，因而原子储存时间的设计是氢脉泽小型化的一个重要问题.小型化主动型氢钟的指标因小型化的程度而有所差别.Zivanov等^[12-14]研制出仅重35 kg的采用蓝宝石介质腔的氢脉泽，原子储存泡体积为1.7 L，稳定度可达1×10^-15/d.国内的杨仁福等^{[15, 16]}等也研制了采用蓝宝石介质腔的氢钟，原子储存泡体积为0.7 L，稳定度达3×10^-15/d.但对氢脉泽小型化引起的问题的全面分析或评估还未见到相关报道.

本文对采用介质加载谐振腔的小型化氢脉泽的原子储存时间进行了设计，对其准确度、稳定度和漂移率指标进行了分析或评估，并测量了其中期稳定度.

1 原子储存时间设计的理论依据 1.1 原子储存时间对氢脉泽频率稳定度的影响

在氢脉泽中，磁选态器使处于超精细磁子能级$\left| {F = 1, {m_F} = {\rm{0}}} \right\rangle $和$\left| {F = 1, {m_F} = {\rm{1}}} \right\rangle $（无效态，增加碰撞弛豫）两个态的氢原子聚焦而进入原子储存泡，氢原子在原子储存泡中与泡壁发生多次碰撞并最终经储存泡准直器口逃逸.氢原子逃逸储存泡、氢原子之间的自旋交换碰撞弛豫（与氢原子束流大小相关）、氢原子与泡壁的碰撞弛豫，以及C场不均匀引起的磁弛豫是几个主要的弛豫项.氢脉泽自持振荡的形成对腔品质因子Q_c和填充因子η、原子储存时间T_b、氢原子的自旋交换碰撞散射截面σ_ex等参数有严苛的要求，常用这些参数构成的品质因子q来表征，其取值范围仅为0~0.172，典型值为0.08.同时，氢原子束流也需控制在起振阈值束流4倍左右的小范围内.这样既能维持氢脉泽合适的振荡功率大小；又能避免因储存泡内原子密度过大引起的自旋交换碰撞弛豫过大，以及进一步对振荡功率和频率稳定度的影响.

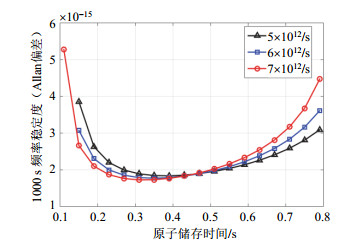
从氢原子系综宏观磁矩（密度矩阵方法计算）对谐振腔电磁场模式微扰的角度，可以建立氢脉泽的半经典理论，定量计算氢脉泽的振荡功率和振荡频率.氢钟中长期稳定度主要受限于谐振腔内热辐射引起的白频率噪声和频率漂移，对于热噪声决定的频率稳定度的定量分析，需要综合考虑原子的各种弛豫对脉泽功率和谱线线宽的影响.当采用介质加载谐振腔缩小谐振腔的体积时，原子储存泡的体积自然也变小.由于原子储存时间和氢原子束流会影响泡壁碰撞和自旋交换碰撞的弛豫时间，进而影响谱线品质因子、脉泽功率和频率稳定度，因而对于小型化氢脉泽需要充分考虑这些效应.图 1给出原子储存泡小型化后，腔内热辐射白频率噪声决定的频率稳定度随原子储存时间和氢原子束流的变化，在计算过程中，先后依次计算了各项弛豫时间、脉泽功率和频率稳定度，相关计算公式可参阅文献[17].从图 1中可以看出，原子储存时间对频率稳定度的影响很大，对于这种小型化氢脉泽，为使中期频率稳定度最优，最优原子储存时间需设计在0.4 s左右，而传统氢脉泽的最优原子储存时间设计值约为1 s.在选择较优原子储存时间和原子束流的基础上，小型化和传统氢脉泽的氢原子自旋交换碰撞和泡壁碰撞弛豫时间的典型值对比如表 1所示.

图 1 小型化氢脉泽1 000 s频率稳定度与原子储存时间的关系.蓝宝石储存泡体积为0.7 L.不同的线型表示不同的原子束流 Fig. 1 Relationship of 1 000 s frequency stability of the miniaturized hydrogen maser with the storage time. The volume of the sapphire storage bulb is 0.7 L, the different lines represent the different beam flux intensity of hydrogen atoms

表 1 氢脉泽中氢原子的主要弛豫时间评估值（313 K）.小型化和传统氢脉泽的原子束流分别为7×10¹²/s和4×10¹²/s Table 1 The typical relaxation values of hydrogen atoms in hydrogen masers (313 K). The beam flux intensity of the miniaturized hydrogen maser and the traditional hydrogen maser are respectively 7×10¹²/s and 4×10¹²/s

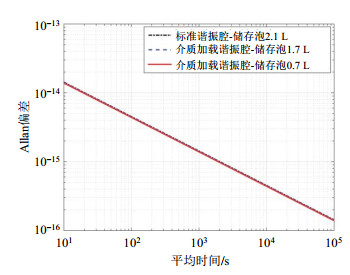
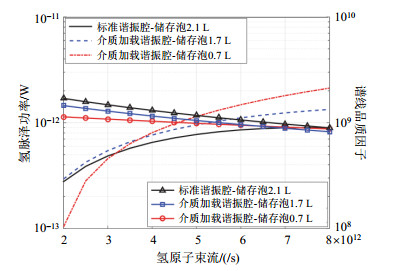
随着储存泡体积的减小，在原子束流相同的情况下，氢脉泽热噪声决定的极限频率稳定度也会相应地变差.当氢原子束流较小时（例如，2×10¹²/s~3×10¹²/s），氢脉泽的小型化会使频率稳定度有较明显的恶化（相同平均时间的频率稳定度系数增大1倍多）；但随着原子束流的增大，这种恶化程度越来越小.例如，针对三种腔-泡尺寸不一样的氢脉泽，当原子储存泡体积分别为2.1 L、1.7 L和0.7 L时，原子储存时间分别为1.0 s、0.8 s和0.4 s.当有效氢原子束流设定为5×10¹²/s时，白频率热噪声决定的频率稳定度如图 2所示.可以看出，氢脉泽小型化后频率稳定度没有明显恶化.这是因为当氢原子束流较小时，相较于传统氢脉泽，小型化氢脉泽的谱线品质因子（Q_l）和振荡功率都较小，稳定度自然发生明显恶化；但当原子束流较大时，相较于传统氢脉泽，尽管小型化氢脉泽的Q_l仍然较小，但振荡功率会大于传统氢脉泽，小型化后频率稳定度就不会发生明显恶化（图 3）.但介质加载谐振腔（储存泡0.7 L）氢脉泽的Q_l降低至8×10⁸左右，约是传统氢脉泽（标准谐振腔-储存泡2.1 L）Q_l值（约15×10⁸）的1/2，使得腔频对振荡频率的牵引因子增大了约1倍，从而使得振荡频率更易受腔频波动的影响.

图 2 白频率热噪声决定的频率稳定度.原子束流为5×10¹²/s Fig. 2 Dependence of the frequency stability related to the white frequency noise component of the thermal noise on the volume of storage bulb. The beam flux intensity of hydrogen atoms is 5×10¹²/s

图 3 氢脉泽功率和谱线品质因子与氢原子束流的关系.储存泡体积为2.1、1.7和0.7 L时，对应的原子储存时间分别为1.0、0.8和0.4 s Fig. 3 Dependence of the hydrogen maser power and the quality factor of the atomic resonance line on the hydrogen atom flux intensity. The atomic storage time of 2.1, 1.7 and 0.7 L storage bulbs are 1.0, 0.8 and 0.4 s respectively

1.2 小型化对氢脉泽准确度和漂移率的影响

采用这种小型化的方案，会增大泡壁碰撞频移（壁移）和频率漂移率.储存泡内原子密度的增加，导致壁移和自旋交换碰撞频移增大.但壁移不确定度由测量不确定度决定，采用同样测量壁移的方法，并不会增大频移不确定度，不影响准确度.经过自旋交换调节，氢脉泽的振荡频率为^{[17, 18]}:

${\omega _{\rm{t}}} - {\omega '_0} = - 2\frac{{{\varepsilon _{\rm{H}}} + {\varepsilon _{\rm{M}}}}}{{{T_{20}}}}$

(1)

其中，${\omega _{\rm{t}}}$为振荡频率，${\omega '_0}$为包含二阶多普勒频移、壁移和C场频移后的钟跃迁频率；$1/{T_{20}} = 1/{T_2} - 1/{T_{2e}}$，${T_2} = 2{Q_{\rm{l}}}/{\omega _0}$，${T_2}$和${T_{2e}}$分别为氢原子的总横向弛豫时间和自旋交换碰撞横向弛豫时间，${Q_{\rm{l}}}$为谱线品质因子；${\varepsilon _{\rm{M}}}$与$\left| F \right. = 1, {m_F} = \left. {1\, } \right\rangle $和$\left| F \right. = 1, {m_F} = \left. { - 1\, } \right\rangle $能级的原子布居数差，以及射频场和C场不均匀有关，${\varepsilon _{\rm{H}}}$与原子自旋交换碰撞过程引起的原子与射频场相互作用中断有关^[18]，${\varepsilon _{\rm{M}}}$和${\varepsilon _{\rm{H}}}$都是频移因子.对(1)式求导，可得理想自旋交换调节下的氢钟漂移率：

$\frac{{{\rm{d}}[({\omega _{\rm{t}}} - {{\omega '}_0})/{{\omega '}_0}]}}{{{\rm{d}}t}} = \frac{{{\varepsilon _{\rm{H}}} + {\varepsilon _{\rm{M}}}}}{{Q_{_{\rm{l}}}^2}}\frac{{{\rm{d}}{Q_{\rm{l}}}}}{{{\rm{d}}t}}$

(2)

其中，${\rm{d}}{Q_{\rm{l}}}{\rm{/d}}t$间接反映泡壁的老化率.当0.7 L的原子储存泡原子储存时间设计为0.4 s时，单位时间内泡壁（特氟龙膜）受原子碰撞的总次数是传统储存泡的2倍以上，所以$\left| {{\rm{d}}{Q_{\rm{l}}}{\rm{/d}}t} \right|$会增大.另外，${\varepsilon _{\rm{M}}}$和${\varepsilon _{\rm{H}}}$也可能增大，而且${Q_{\rm{l}}}$从约15×10⁸减小至8×10⁸，这些变化都会使漂移率增大，从而影响氢钟的长期稳定度.

2 介质加载谐振腔原子储存时间的设计和实现

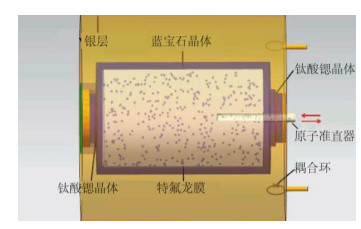
在小型化氢脉泽中，我们设计了低腔频-温度系数的介质加载腔^[19].将蓝宝石晶体（晶型为型的Al₂O₃晶体）放置在内壁镀银的金属腔体中，蓝宝石晶体是中空的，将其内壁涂敷特氟龙分散液，并烧结成特氟龙膜而作为原子储存泡，外壁与金属腔体间也有一定的间隙以安装耦合环.为了方便调节腔频，在40 ℃时，腔频-温度系数为-12.5 kHz/K的介质加载谐振腔被采用.

原子通过准直器泄流的过程是一个复杂的过程^{[18, 20]}，准直器的长度与截面半径之比（L/a）是一个很重要的量.当准直器的长度远小于其截面半径时，原子与准直器的内壁碰撞后将不能返回储存泡；而当准直器的长度与其截面相当时，原子与准直器的内壁碰撞后将可能返回储存泡.根据氢脉泽的物理原理，设计好原子储存时间后，就可以根据小孔泄流的理论，设计准直器的长度和截面半径来实现原子储存时间^[18].在初期的自激振荡实验中，没有仔细考虑原子储存时间的设计，泡口直径设计为7.0 mm，与泡口相连的准直器长度设计为28 mm时，原子储存时间约为0.11 s.为了实现0.4 s的原子储存时间，将泡口直径设计为5.8 mm，准直器长度设计为66 mm，介质加载谐振腔和储存泡的等比例结构图如图 4所示.

图 4 介质加载谐振腔和储存泡结构 Fig. 4 The schematic diagram of the dielectric loaded cavity and storage bulb

通过观测氢原子束流很小情况下的Rabi振荡现象，可以间接验证原子储存时间的设计.Rabi振荡和自由感应衰变的测量方法如图 5所示.其中，原子束流要低于自激振荡的阈值束流，使氢脉泽不能维持自激振荡，且微波探寻信号和氢原子束流都需要时序控制.通过单片机来控制继电器，实现对电离源通断的时序控制，以时序控制有无原子束流进入储存泡.在网络分析仪（加10 MHz外参考）输出端串联两个数字衰减器（衰减器芯片型号为HMC273MS10G），通过另一片单片机来控制数字衰减器的衰减值，实现对网络分析仪输出的连续微波信号的时序衰减，即控制微波探寻信号的时序通断，控制方法与文献^[21]中的方法类似.

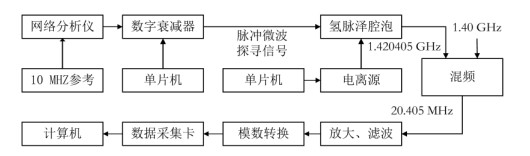
图 5 Rabi振荡和自由感应衰变测量方法框图 Fig. 5 The system block diagram for measuring Rabi oscillation and the decay of the induced microwave magnetic induction

在测量过程中，先给电离源加持续7 s的电压，在此期间氢原子进入储存泡，且储存泡内氢原子数很快达到稳定.然后断开电离源电压，与此同时通过微波开关给微波腔注入长达0.8 s的弱激励信号（功率为-67~ -77 dBm），微波探寻信号与原子系综相互作用过程中，经另一个耦合环输出的微波信号和一路1.42 GHz信号混频，下变频为20.405 MHz的信号，经放大和滤波（带宽2 kHz），送入模数转换模块检波（芯片型号为AD8307），检波电压送入数据采集卡进行收集.如图 6(a)~(c)所示，Rabi振荡导致的Rabi章动被观测到.可以明显地看到，不同功率的探测信号，Rabi章动的频率不一样；Rabi章动零点位置降低是由于在切断原子束流后，储存泡内的原子数因逃逸在逐渐减少；振荡幅度减小是原子系综逐渐失去相干性和原子数逐渐减少的结果.通过观察Rabi章动现象，有助于理解氢脉泽的动力学过程，并且可以据此选择适当功率的激励信号和相应的脉冲宽度来观察自由感应衰变信号.在切断氢束流的同时，给微波腔注入时长为50 ms的激励信号，自由感应衰变信号如图 6(d)所示.可以看出，原子系综发射电磁波的幅度衰减至初始幅度1/2，约需0.25 s，考虑到自由感应衰变按${{\rm{e}}^{ - t/{T_2}}}$规律衰减^[18]，所以横向弛豫时间T₂约为0.25 s.由于此时原子束流较小，自旋交换碰撞横向弛豫一般很小，同时考虑到磁弛豫（设置为2 s）和泡壁碰撞横向弛豫，估算得T_b约为0.48 s，与原子储存时间的设计值基本相符.

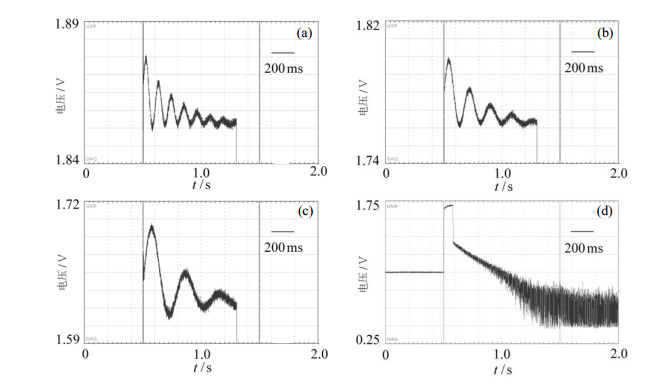
图 6 Rabi章动和自由感应衰变.(a)激励功率为-67 dBm；(b)激励功率为-72 dBm；(c)激励功率为-77 dBm；(d)激励功率为-70 dBm.脉宽为50 ms Fig. 6 The Rabi nutation and decay of the induced microwave magnetic induction. (a) Excitation power of -67 dBm; (b) Excitation power of -72 dBm; (c) Excitation power of -77 dBm; (d) Excitation power of -70 dBm. Pulse width is 50 ms

3 中短期频率稳定度结果和讨论

将本文设计的介质加载谐振腔替换SOHM-4传统型氢脉泽的谐振腔，构成新型氢脉泽的验证平台.测量得到原子储存时间为0.11 s和0.4 s时，氢脉泽起振的原子阈值束流分别约为0.30 mA（离子泵电流）和0.14 mA，原子谱线Q_l值分别约为4×10⁸和8×10⁸.分别将两种储存时间的氢脉泽和接收机闭环锁定，将其输出的5 MHz信号与VCH-1003A型氢钟的5 MHz信号通过TSC-5120A相位噪声分析仪进行比对，比对的相位差原始数据经远程传递至计算机，用stable 32画出频率稳定度.当原子储存时间为0.11 s时，100 s和1 000 s的频率稳定度分别为3.5×10^-14和1.5×10^-14；当原子储存时间为0.40 s时，100 s和1 000 s的频率稳定度分别为1.5×10^-14和5.6×10^-15.两种情况下的频率稳定度比较如图 7所示.比对在温度波动大于±1 ℃的房间内完成，受环境温度波动的影响较大，且实验平台的力学结构也不稳定，因而两种情况的频率比对分别只进行了5.5 h和14 h，未进行更长时间的频率比对.按照小型化氢脉泽原子储存时间设计的对比实验计划，还需测量原子储存时间为0.2 s、0.3 s和0.5 s时的中短期频率稳定度表现，但考虑到已获得较好的实验结果，且反复打开真空更改原子储存时间会对储存泡壁带来不利影响，就未进一步更改原子储存时间和分别进行闭环锁定实验.

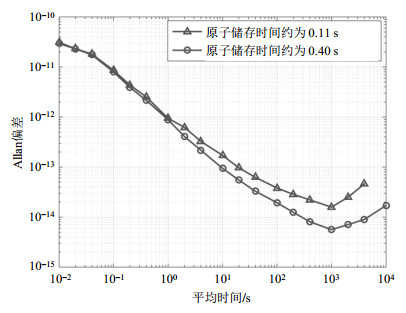
图 7 采用介质加载谐振腔（储存泡体积0.7 L）的氢脉泽频率稳定度 Fig. 7 The frequency stability of the hydrogen master employing the new dielectric loaded cavity (the volume of storage bulb is 0.7 L)

尽管频率比对的时间不够长，但已足以评估平均时间1~1 000 s的频率稳定度，且100 s和1 000 s的频率稳定度指标充分体现了物理部分的性能.可以看出，原子储存时间由0.11 s变为0.40 s时，氢脉泽的100 s和1 000 s频率稳定度改善了2倍多，这个比例与图 1的理论分析是基本相符的，实验结果验证了小型化氢脉泽原子储存时间设计的合理性.两种情况下测量得到的100 s和1 000 s稳定度与图 1所示的理论值相差2~3倍，1~10 s的短期稳定度也较差，我们认为这是由电子学系统噪声较大引起的.

上述小型化氢脉泽设计仍有改进的空间.闭环过程中采用了无负载腔探寻的腔频自动调谐方式，探寻信号的调谐频率仅为1 Hz，可以看成是以频率为氢脉泽振荡频率${f_{\rm{0}}}$的信号为载波的方波频率调制.将其作傅里叶展开，在频率为(${f_{\rm{0}}} \pm n$)（n为正整数）处有分波.在原子线宽未展宽时，调制信号在${f_{\rm{0}}}$附近的频谱成分与原子谱线交叠小；在原子线宽增宽时，调制信号在${f_{\rm{0}}}$附近的频谱成分与原子谱线交叠增大，小型化氢脉泽和传统氢脉泽的谱线与调制信号的交叠如图 8所示.调制信号与原子跃迁谱线的交叠引入了附加相位噪声，会影响频率稳定度.如果采用腔频切换的调谐方式或者增大无负载腔探寻调谐方式调制频率，减弱调谐信号对脉泽谱线的影响，频率稳定度还可以再提高.当然，要获得较好的长期稳定度，还需要针对这种小型化腔泡设计好力学和恒温等外围结构.

图 8 腔频自动调谐探寻信号频谱对脉泽谱线的影响.曲线1和曲线2分别为小型化氢脉泽和传统氢脉泽的脉泽谱线；梳状谱3表示腔频自动调谐探寻信号的频谱 Fig. 8 Influence of signal spectrum of cavity frequency auto-tuning on the maser spectrum line. Curves 1 and 2 correspond to the miniaturized hydrogen maser and the traditional hydrogen maser respectively, comb spectrum 3 corresponds the frequency spectrum of the modulating signal of cavity frequency auto-tuning

实测5 MHz信号的相位噪声谱（图 9）显示：当f < 0.01 Hz时，相位波动功率谱密度S_Φ∝f^-2，$\mathscr{L}$(f)=10×lg[$\frac{1}{2}$S_Φ(f)]；频率波动功率谱密度S_y∝f⁰；对应热力学白频率噪声，σ_y (τ > 50 s)∝τ^-1/2；当0.01 Hz < f < 0.5 Hz时，是一个过渡区域，S_Φ∝f^-1，S_y∝f¹，σ_y (1 s < τ < 50 s)∝τ^-1；当0.5 Hz < f < 5 Hz时，S_Φ∝f⁰，S_y∝f²，σ_y (0.1 s < τ < 1 s)∝τ^-1，对应热力学白相位噪声；A指物理部分噪声和电子学噪声在频域的分界点.对于0.5 Hz附近的异常凸起，目前还没有合理的解释.

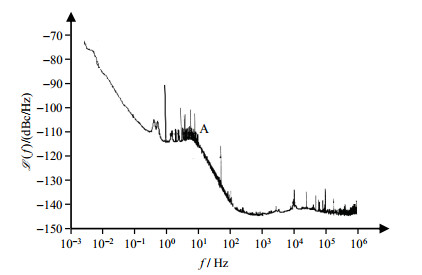
图 9 5 MHz输出信号相位噪声.储存时间为0.4 s Fig. 9 The phase noise in frequency domain of the 5 MHz output signal. The storage time is 0.4 s

4 结论

本文基于对小型化氢脉泽的仿真计算和分析，实现了对小型化氢脉泽原子储存时间的设计，在实验上将介质加载谐振腔储存泡（体积0.7 L）的原子储存时间调控至约0.4 s，闭环后频率稳定度达5.6×10^-15/(1 000 s)，且频率稳定度指标可通过改变腔频探寻的调制方式和改进电子学得到进一步提升.因此，在进行氢脉泽小型化设计时，需要综合考虑原子多项弛豫时间的变化，通过设计原子储存时间来实现对多项弛豫时间的调整.总体来说，采用介质加载谐振腔取代传统氢脉泽的腔-泡结构，可以有效地缩小主动型氢原子钟的体积和重量，但是频率稳定度会略低于传统主动型氢钟，并且腔频波动对振荡频率的牵引变大，同时频率漂移率也会相应增大.

参考文献

[1]	KLEPPNER D, GOLDENBERG H M, RAMSEY N F. Theory of the hydrogen maser[J]. Phys Rev, 1962, 126: 603-608. DOI: 10.1103/PhysRev.126.603.
[2]	PETERS H E. Hydrogen masers using cavity frequency-switching servos:Present system design and possible improvements[J]. Metrologia, 2006, 43: 353-360. DOI: 10.1088/0026-1394/43/5/003.
[3]	DEMIDOV N, VORONTSOV V, BELYAEV A, et al. Studies of a short and long-term stability of an hydrogen maser with stand alone cavity auto tuning[C]. Gothenburg: Proceedings of 26th European Frequency and Time Forum Meeting. USA: IEEE, 2012: 488-493.
[4]	ALEYNIKOV M S, BLINOV I Y. Parameters of double selection of atoms in a hydrogen maser and the use of its signal in a fountain-type frequency standard[J]. Meas Tech+, 2015, 58(8): 892-897. DOI: 10.1007/s11018-015-0813-0.
[5]	ALEYNIKOV M S. A study of atomic magnetic transitions during operation of an H-maser double-state selection system[J]. Meas Tech+, 2016, 59(3): 235-238.
[6]	BOYKO A I, ALEYNIKOV M S. An active hydrogen maser with enhanced short-term stabilit[J]. Meas Tech+, 2014, 56(10): 1140-1145. DOI: 10.1007/s11018-014-0345-z.
[7]	ALEYNIKOV M S. Magnetic state selection impact on double resonance effect in H-maser[C]. New Orleans: 2016 IEEE International Frequency Control Symposium (IFCS), 2016.
[8]	LAURENT P, MASSONNET D, CACCIAPUOTI L, et al. The ACES/PHARAO space mission[J]. CR Phys, 2015, 16(5): 540-552. DOI: 10.1016/j.crhy.2015.05.002.
[9]	LITVINOV D A, RUDENKO V N, ALAKOZ A V, et al. Probing the gravitational redshift with an earth-orbiting satellite[J]. Phys Lett A, 2018, 382(33): 2192-2198. DOI: 10.1016/j.physleta.2017.09.014.
[10]	ASHBY N, HEAVNER T P, JEFFERTS S R, et al. Testing local position invariance with four cesium fountain primary frequency standards and four NIST hydrogen masers[J]. Phys Rev Lett, 2007, 98(7): 070802. DOI: 10.1103/PhysRevLett.98.070802.
[11]	TURYSHEV S G, NAN YU, TOTH V T. General relativistic observables for the ACES experiment[J]. Phys Rev D, 2016, 93: 045027. DOI: 10.1103/PhysRevD.93.045027.
[12]	JORNOD A, GOUJON D, GRITTI D, et al. The 35kg space active hydrogen maser (shm-35) for ACES[C]. Tampa: Proceedings of the 2003 IEEE International Frequency Control Symposium and Pda exhibition Jointly with 17th European Frequency and Time Forum, 2003: 82-85.
[13]	ZIVANOV S, SCHWEDA H, GOUJON D, et al. Physics package of the 35kg space active hydrogen maser for the ACES space mission of ESA[C]. Geneva: Proceedings of the IEEE International Frequency Control Symposium Jointly with the 21st European Frequency and Time Forum, 2007: 637-641.
[14]	SCHWEDA H, ZIVANOV S, PERRUCHOUD G, et al. Performance demonstration of the onboard active hydrogen maser for the ACES space mission of ESA[C]. Geneva: Proceedings of the IEEE International Frequency Control Symposium Jointly with the 21st European Frequency and Time Forum, 2007: 1116-1121.
[15]	YANG R F, ZHOU T Z, CHEN H B, et al. A new method to reduce frequency-temperature coefficient of sapphire loaded cavities for compact hydrogen masers[J]. IEEE Trans Ultrason Ferroelectr Freq Control, 2010, 57(3): 583-586. DOI: 10.1109/TUFFC.2010.1450.
[16]	YANG R F, ZHOU T Z, WANG N R, et al. Designs of a miniaturized sapphire loaded cavity for space-borne hydrogen masers[J]. IEEE Trans Ultrason Ferroelectr Freq Control, 2010, 57(3): 587-591. DOI: 10.1109/TUFFC.2010.1451.
[17]	VANIER J, AUDOIN C. The quantum physics of atomic frequency standards[M]. Philadelphia: IOP Publishing Ltd, 1989: 452-1015.
[18]	CRAMPTON S B, WANG H T M. Duration of hydrogen atom spin exchange collisions[J]. Phys Rev A, 1975, 12: 1305-1312. DOI: 10.1103/PhysRevA.12.1305.
[19]	HE K L, ZHANG W Q. Study on miniaturized hydrogen maser with dielectric loaded resonance cavity[J]. Chinese Journal of Scientific Instrument, 2016, 37(5): 1164-1171. 何克亮, 张为群. 介质加载谐振腔的小型化氢脉泽的研究[J]. 仪器仪表学报, 2016, 37(5): 1164-1171.
[20]	王义遒, 王庆吉, 傅济时, 等. 量子频标原理[M]. 北京: 北京大学出版社, 1986: 424.
[21]	CHEN P F, XIE Y H, LIN C F. Induction of hydrogen ramsey interference with pulsed microwave[J]. Chinese J Magn Reson, 2013, 30(3): 361-370. 陈鹏飞, 谢勇辉, 林传富. 脉冲微波激发氢原子Ramsey干涉研究[J]. 波谱学杂志, 2013, 30(3): 361-370. DOI: 10.3969/j.issn.1000-4556.2013.03.006.