扩散张量成像(Diffusion Tensor Imaging,DTI)可以通过检查组织中水分子的三维位移分布来研究脑部结构[1].由于人脑结构具有较大的个体差异性,通过对不同个体的扩散磁共振图像进行组间分析时,常常需要一个公共的标准空间,保证用于不同个体图像的组织扩散信息对应于同一空间位置.通过DTI技术检测健康受试者和患者之间的脑组织微小差异,目前已被各种脑疾病研究采用,如精神分裂症[2]、躁郁症[3]、脑中风[4]、老年痴呆[5]和创伤性脑损伤[6]等.这些脑疾病可采用感兴趣区域(Region of Interest,ROI)法或者基于体素分析(Voxel-Based Analysis,VBA)法进行组间差异比较.ROI法是通过手动或半自动选取ROI,然后比较组间选取的ROI[7],然而由于各受试者的大脑定位不同,ROI法并不能对主要扩散方向的数量进行比较;VBA法是以像素作为解析的最小单位,将扩散图像中的所有像素作为解析对象,并逐一像素地进行统计分析.但是无论是ROI法还是VBA法,都需要把每组数据空间标准化到扩散模板后再进行后续的组间比较[3, 8].扩散张量脑模板包含丰富的大脑组织信息,并能在空间标准化或者脑图谱的发展中提供参考.具有代表性的平均人脑微观结构的扩散模板可以通过结合多个个体受试者的扩散信息构建,并用于人群中脑微观结构的比较以及生成数字脑图谱[9].通过使用脑模板,研究者可以在一个标准空间中比较或者组合不同个体同一模态的脑部图像、同一个体不同模态的图像(扩散张量成像、磁共振T1加权像、功能磁共振图像),甚至不同脑部状态的图像(健康志愿者图像或者脑部病人图像)等.
DTI能够提供关于活体脑组织的微观结构信息[10],张量中的主方向可以用于构建脑连接信息.患者和健康受试者间扩散张量的综合性比较需要将所有受试者的DTI数据进行空间标准化,因此实现空间标准化的配准精准度就显得极为重要.目前基于DTI数据构建的DTI脑模板一直在不断改进配准方法,使得脑模板具有更高的空间分辨率和对比度,并能够分辨出更微小的白质纤维.然而DTI技术只能显示人脑组织内的单纤维束,对于交叉、分支和汇聚纤维的情况处理方法还不成熟.为此研究者又基于高分辨率扩散成像,包括扩散频谱成像(Diffusion Spectrum Imaging,DSI)和高角度分辨率扩散成像(High Angular Resolution Diffusion Imaging,HARDI)构建出高分辨率扩散张量脑模板,解决了单个体素内多纤维取向的难题,同时提高了扩散张量脑模板中复杂神经元微观区域的精度.
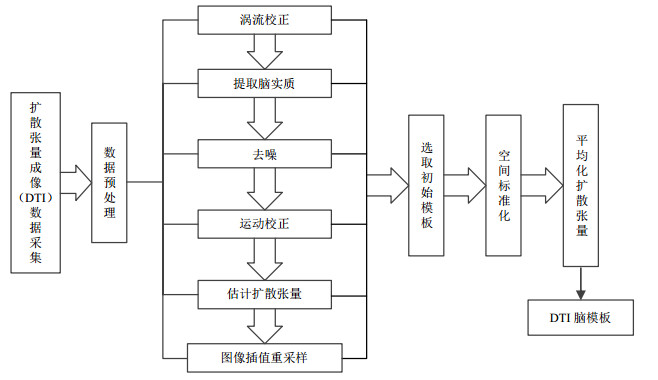
1 DTI脑模板DTI脑模板在一定程度上代表了人脑微观结构,对于比较神经元结构的完整性和群体间的脑连接性有重要意义,并且为构建一个扩散信息详尽的白质图谱提供了参考.DTI能提供有关的结构完整性和体内脑白质纤维定位信息,通过纤维束追踪成像可以追踪白质纤维束的路径.既往研究中,DTI脑模板构建的一般步骤如图 1所示:1)选取受试者,采集DTI数据以及b=0 s/mm2图像;2)DTI数据预处理,包括涡流校正、脑实质提取、去噪、运动校正、扩散张量估计和图像插值重采样;3)选取临时模板,把DTI数据配准到临时模板空间,完成空间标准化;4)扩散张量平均化,构建最终DTI脑模板.尽管既往研究在构建标准扩散张量脑模板方面已经取得不少成果,但是DTI脑模板的研究仍存在不足.
|
图 1 DTI脑模板构建流程图 Figure 1 Flow chart of DTI brain template construction |
最早涉及全张量研究的是Jones扩散张量脑模板.2002年,Jones等人[11]选取11位(33.3±4.7)岁的受试者进行研究,采用仿射变换把10位受试者的部分各向异性(Fractional Anisotropy,FA)图线性配准到剩余1个受试者的FA图,然后将变换使用的参数应用于重新定位扩散张量,并通过计算扩散张量分布的中位数的方法获取张量分布模式.神经影像领域最常见的汇总统计数据的方法是计算分布的平均值,然而在可能存在离群值的情况下就需要检验分布的中位数,这是第一次通过计算中位数的方法制定二阶张量的分布以获取张量分布模式的“粒状”外观,为后续脑模板的研究奠定了重要基础.该模板第一次通过仿射变换实现了全张量数据集的空间标准化,但是仿射变换是将源图像进行平移、旋转、缩放及剪切操作映射到参考图像中,其形变形式为直线映射到直线[12],大脑是人体内最为复杂的器官,其图像信息包含众多形状各异的解剖结构,如海马体和脑回沟等,因此仿射变换的结果较难达到最终模板用于图像分析的精准性要求.另外,该模板的FA图是通过平面回波成像(Echo Planar Imaging,EPI)序列采集,涡流及磁场非均匀的影响会对图像造成伪影,引起图像失真,且由于受试者的年龄差异较大而导致图像具有不同的扩散特性.此外利用中位数制定的二阶张量分布需要在较多的受试者群体内才能体现出统计特性,而且此研究仅有11位受试者,因此Jones扩散张量脑模板并不能应用于普遍人群的脑疾病研究.
1.2 Park-DTI脑模板为了弥补Jones扩散张量脑模板用于研究的缺陷,Park等人[13]于2003年构建出多通道空间标准化扩散张量脑模板.该模板选取的16位受试者图像数据是基于线扫描(Line-Scan)序列扫描而来,相对于EPI序列,线扫描对运动及磁敏性伪影不敏感,且具有更高的空间分辨率,可以清晰显示出脑干区域的纤维状态.研究者们采用基于Demons的多输入通道配准算法将16位受试者的数据集分别进行非线性配准,包括T2加权密度单通道、部分各向异性单通道、第一和第二特征值的差分单通道、部分各向异性和张量路径的双通道和张量特征值的三通道以及六通道张量分量.最终发现,六通道张量分量作为输入通道能有效地对纤维束形态以及张量取向进行标准化,同时使用平均张量场以及平均形变场的非线性方法构建出最终扩散张量脑模板.Park模板较Jones扩散张量脑模板具有更好的精准度和较高的图像分辨率,但是这两个脑模板均是由1.5 T MRI扫描仪采集的图像构建而来,获取的信噪比较低,因而影响整个模板的分辨率.
之后Zhang等人[14]、Muller等人[15]也对扩散张量脑模板进行了研究,这些构建DTI脑模板研究方法的总体特点如下:1)EPI序列相关的图像伪影会影响最终脑模板的精准度;2)采用仿射变换而不是非线性配准进行空间归一化;3)单标量进行空间标准化会导致DTI信息的缺失;4)受试者的数量较少,不具备普遍性且不同年龄段的受试者具有不同的扩散特性等.所以这些扩散张量脑模板并不适用于普遍人群的脑疾病研究.
1.3 ICBM-DTI-81脑模板研究证明,基于少量受试者构建的群体DTI模板具有相对较高的可变扩散特性,但随着受试者数量增大,这种可变性逐渐减少,受试者超过约60人时将会生成一个高度稳定的模板[16].2008年,Mori等人[17]选取81位年龄段在18~59岁的受试者进行研究,根据颜色编码的FA图手动勾画出纤维路径区域,构建了第一个群体数量较大的立体定位白质模板,该模板融合了现有的ICBM-152(International Consortium for Brain Mapping,ICBM)解剖模板的空间坐标系与DTI数据的白质信息.此研究评估该模板配准精度时,采用四阶多项式变换把其中9位受试者非线性配准到生成的白质模板,提升了评估实验的配准精度,但构建该白质模板时均采用的是自动图像配准(Automated Image Registration,AIR)软件[18]中的12模式仿射变换,仿射变换的结果较难达到最终模板用于图像分析的精准性要求.此外,不同年龄组间受试者的白质解剖结构具有显著差异,而此研究中的受试者年龄范围在18~59岁,因此该模板不能应用于特定年龄段受试者的脑研究中.
1.4 ENIGMA脑模板DTI能生成随大脑发育或退化的敏感性定量指标,且一些常见的遗传变异可能与白质的完整性及连接性有关,DTI的指标参数,如水扩散的FA图,可用于识别影响脑微观结构的遗传变异体,这对于进一步研究遗传性基因非常有前途[19].虽然这些遗传变异体的研究对于人脑疾病的发现具有重大意义,但是单个成像组发现的遗传变异体却不能可靠地推广到其他人群.此外,如果同一群体是通过不同扫描参数进行成像或不同处理流程进行图像分析时,对于同一种脑疾病可能在关于遗传变异体的结论方面存在差异[20].为了解决这些问题,Meta分析优化神经成像遗传学(Enhancing Neuro Imaging Genetics through Meta-Analysis,ENIGMA)联盟通过分析北美洲、澳大利亚和欧洲多个成像组的高分辨率FA图指标来解决多个站点采集数据协调成像的问题[21].研究者们分别从4个不同分辨率以及不同群体结构的成像组中随机选取100个受试者的FA图像,采用FMRIB软件库(FMRIB Software Library, FSL)中的flirt线性变换[22]把所有受试者的FA图像配准到ICBM-DTI-81[17]模板来保证空间一致性;然后从这些变换后的图像中构建了一个临时模板[23, 24];接着每个成像组中的100个受试者的FA图像进行循环非线性配准到临时模板来构建出最终的通用模板,下载地址见表 1.该模板使不同成像组的图像变换到相同的高分辨率立体空间并沿着同一空间的白质架构进行遗传变异体基于体素的Meta分析,解决了各成像组间图像的分辨率及空间不一致以及单个成像组数据较为单一的难题,对脑疾病基因遗传变异体上的研究具有重要价值.但是ENIGMA模板选取的受试者均来自4个成像组的家系研究,是作为分析特定脑疾病中遗传变异体的通用模板,用于一般群体的研究并不合适.
| 表 1 常用DTI人脑模板的下载地址列表 Table 1 The download links of common DTI human brain templates |
随着神经影像学研究的发展,2009年,伊利诺理工大学(Illinois Institute of Technology,ⅡT)生物医学系的Peng等人[25]选取了年龄段为20~40岁具有相似扩散特性的67名健康受试者,采集Turboprop-DTI序列扫描出的最小化图像伪影数据[26],先构建出一个临时的DTI模板,然后把平均扩散加权图像和部分各向异性图像非线性配准转换到临时模板的空间,再把平均变换应用于个体受试者的扩散张量体素,最后平均所有受试者的扩散张量构建出ⅡT脑模板.该模板具有较高的图像分辨率,并且能够分辨较小的白质纤维,解决了前人研究的脑模板图像分辨率较差的问题.然而ⅡT模板在构建时采用低维度配准,导致受试者间的扩散信息在三维空间内不匹配,最终表现为局部扩散信息的缺失以及最终张量产生误差.为了解决ⅡT脑模板用于研究的缺陷,Zhang等人[27]于2011年使用ⅡT模板的原始数据并采用高维度非线性配准,改进了ICBM-152空间的扩散张量脑模板.同时,为了比较两个模板间的图像对比度、扩散张量特性以及匹配到ICBM-152空间的脑解剖结构精准性,研究者采用一系列的相似性度量进行评估.研究结果表明,ⅡT2模板的扩散张量信息更能代表个体受试者的人脑且图像清晰度更高,解剖结构匹配到ICBM-152空间更为精准.
上述构建DTI脑模板研究方法的主要特点及标准化方式总结见表 2.
| 表 2 DTI人脑模板的各种研究方法及参数表 Table 2 The list of approaches and parameters used in studies on DTI human brain templates |
尽管既往研究在构建DTI脑模板方面已经取得不少成果,但是当人脑中每个体素只有一个主要的扩散方向,即白质单纤维取向时,DTI模型才是有效的.由于DTI需要假设水分子呈高斯扩散,所以在高斯假设的情况下每个受试者的体素中只能单纤维取向[28],这对于90%以上的人脑白质来说是不恰当的假设[29].这种基于扩散张量的模型过于简化,无法解决神经纤维交叉、合并以及分叉等情况,限制了扩散脑模板复杂神经元微结构区域的精度.而DSI和HARDI是不需要依赖任何假设的成像方法,解决了DTI只能提供一个方向的不足,因此研究者们构建出符合人脑白质纤维特点的DSI和HARDI脑模板.
2.1 DSI扩散张量脑模板DSI [30]是一种通过检测水分子的扩散特性来获取神经纤维的物理特征和微观结构的成像方式,它利用概率密度函数(Probability Density Function,PDF)描述扩散运动的空间分布,通过对PDF进行径向加权积分得到的方向分布函数(Orientation Distribution Function,ODF)可以解决纤维交叉等问题,克服了DTI只能提供一个纤维取向的不足.因此,DSI脑模板和图谱比基于DTI构建的脑模板和图谱更能精准地代表平均人脑微观结构.DSI脑模板构建的一般步骤如下:1)选取受试者,采集DSI数据和T1图像;2)DSI数据预处理,包括涡流校正、提取脑实质、去噪、运动校正、计算概率密度函数、获取方向函数以及计算自旋分布函数;3)选取ICBM-152模板,把受试者的T1图像空间标准化到ICBM-152空间,并将此空间变换应用到DSI数据;4)平均化DSI数据,获取初始脑模板;5)通过配准把DSI数据空间标准化到初始模板,进行最终的平均化处理得到DSI脑模板,流程图如图 2所示.

|
图 2 DSI扩散张量脑模板构建流程图 Figure 2 Flow chart of constructing DSI brain template |
2011年,Yeh等人[31]构建了一种高分辨率脑模板NTU-90,这是通过将Q空间微分同胚重建应用到90个DSI数据集并平均自旋分布函数构建而来.该方法使用网格采样方案消除了部分容积效应对图像的影响,同时通过Q空间微分同胚重建计算出转换到ICBM-152空间的自旋分布函数,最后通过平均这90个DSI数据集的转换自旋分布函数构建出最终NTU-90脑图谱.为了验证该方法的准确性,研究者进行了一个仿真研究测试.仿真结果表明,转换后的自旋分布函数可以保持纤维的方向取向,并将解析后的纤维取向用于纤维追踪,生成纤维束,并在转换空间中揭示连接模式.除了模拟研究,Q空间微分同胚重建方法的准确度也在体内数据集进行了定性测试.体内研究结果表明,自旋分布函数可以转化到ICBM-152空间和转换的自旋分布函数的峰值方向与解剖结构相一致.此外还证明,NTU-90图谱的平均化自旋分布函数可以解决交叉纤维且函数值大小可能会反映纤维束填充密度的纤维束.NTU-90图谱主纤维的定量各向异性(Quantitative Anisotropy,QA)映射描述了白质结构,它可以用来定义纤维束的终端,弓状纤维束的成像结果显示出连续的纤维路径以及与语言处理相关的皮质终端.
NTU-90脑图谱能够解决DTI图谱的交叉纤维,并支持纤维交叉区域的纤维跟踪,且能够应用于脑连接的研究中,同时NTU-90图谱的自旋分布函数也可以反映相对纤维群体的变化,以及高填充纤维区域可观测到更大的自旋分布函数.这一特性可能进一步被用来量化大脑连接,但是这项研究构建的大脑图谱也有局限性.首先,所有志愿者都是当地招募的,这个试验库有一个特定的年龄段,并不能完全代表一般人群,显然该图谱并不适用于群体研究.其次,研究者们采集的扩散图像可能会出现额底部分失真,并且在NTU-90图谱中也能观察到该失真.这种易受影响而引起的失真是由于较长的EPI读出序列,可以通过采集额外的区域映射[32],或使用平行成像中更高的加速因子校正.但是研究者们由于在收集数据时应用领域的映射技术和平行成像加速系数是不容易获得的,所以并没有采用上述任何方法以尽量减少失真.此外,NTU-90采用的扩散数据集具有相对较低的空间分辨率(3 mm的各向同性分辨率)与ICBM-152模板的分辨率比较(1 mm的各向同性分辨率),分辨率不高可能导致精细解剖结构的不精确映射,需要更好的空间分辨率来构建高清晰度脑图谱.
2.1.2 NTU-122扩散张量脑模板既往研究中通用的配准方法是将b=0图像或者FA图像配准到ICBM-152模板,但是ICBM-152模板包含结构图像如T1加权图像和T2加权图像,相比于扩散加权图像,ICBM-152模板具有较高的图像对比度、空间分辨率以及信噪比.因此当扩散加权图像直接配准到ICBM-152模板时,两种图像模态上包含的解剖信息如图像对比度、分辨率和信噪比将会出现矛盾,导致出现较低的配准精度.为了解决历年扩散张量脑模板与ICBM-152模板出现解剖结构的不一致性的难题,即有些由脑模板定义的解剖位置并不能精准地匹配到ICBM-152模板,Hsu等人[33]选取了122个平均年龄为(27.97±5.25)岁的健康受试者进行研究.研究者把所有受试者的T1加权图像配准到ICBM-152空间,并将评估的变形图应用到个体受试者的DSI数据集中,以便DSI数据集能临时配准到ICBM-152空间;然后把这些临时配准后的DSI数据集进行平均化处理得到一个中间模板;接着采用LLDMM-DSI算法将临时配准后的DSI数据集变换到中间模板来构建出最终的DSI脑模板NTU-DSI-122.该模板解决了解剖结构不一致性的难题,但是DSI要求的b0值比较大,需要的采样量非常多且采集时间长,限制了其广泛应用.
2.2 HARDI扩散张量脑模板HARDI [34, 35]是扩散磁共振成像方式的一种.相比于DTI,HARDI能够处理交叉、分支、汇聚以及吻合的纤维束,它采集了沿更多方向的扩散加权信号,能够描述非高斯扩散以及解决内部体素异质性即一个体素内多纤维取向的难题.此外,相比于扩散张量模型导出量的部分各向异性,标量描述体素的扩散各向异性以及多纤维取向更精准.因此,HARDI脑模板和图谱比基于DTI构建的脑模板和图谱更能代表平均人脑微观结构.
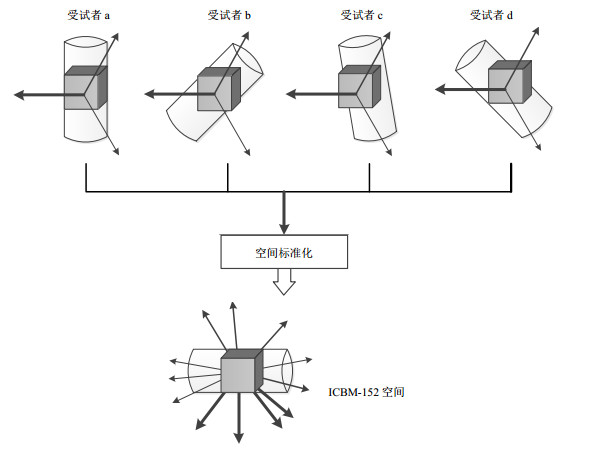
HARDI联合多发射序列在减少图像伪影的同时,对于人脑成像扫描时间过长.为了构建高质量的脑模板,2014年,伊利诺理工大学的Varentsova等人[9]通过把多个受试者的低角度分辨率扩散数据空间配准到ICBM-152空间构建出一个比个体受试者更高角度分辨率的扩散数据集.更具体地说,脑形状和头定位的差异导致了空间标准化时的不同局部旋转,这意味着合并的数据集包含扩散加权对应的所有扩散方向(每个受试者的扩散方向数量×受试者的数量),如图 3所示,在4个不同受试者中,圆柱管代表相同的纤维束,立方体代表图像体素,箭头代表三个扩散梯度向量.第一行,因为大脑形状和头部定位的不同,纤维束在扫描仪的参考帧中是不同的方向.与此相反,因为所有受试者都使用同一扫描仪、脉冲序列和扩散方向集进行扫描,3个扩散梯度向量具有相同方向.每个受试者的组织空间变换到ICBM-152空间需要受试者纤维束的不同旋转.最后一行是通过采用相应的旋转得到变换到ICBM-152空间的对应于扩散加权信号的扩散梯度.此例中,组合4个受试者的弥散加权信号使得一个单一数据集包含沿扩散方向的12个弥散加权信号.该模板选取了72个年龄段在20~40岁的受试者,研究证明这个年龄组的受试者的扩散性质是相对近似的[36].
|
图 3 多个受试者构建联合数据集的流程图 Figure 3 Flow chart of a combined dataset constructed from multiple subjects |
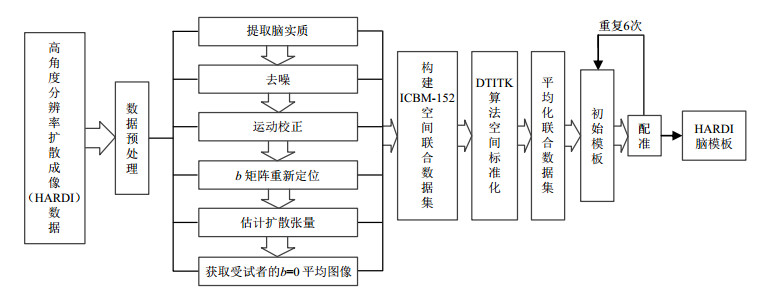
HARDI脑模板构建的一般步骤如下:首先使用TORTOISE软件平台对每个受试者进行脑实质提取,运动校正,b-矩阵重新定位和扩散张量估计;其次获取每个受试者的平均b=0图像,得到的平均b=0图像和预处理后的扩散加权数据变换到ICBM-152空间;然后使用扩散张量成像软件包(Diffusion Tensor Imaging ToolKit, DTITK)算法将72个DTI数据集配准到ⅡT2 DTI脑模板,平均化处理构建一个临时DTI脑模板;最后72个原始DTI数据集配准到临时模板,并对结果进行平均已获得更新的模板,重复这个过程6次,最终将所有数据集变换到群体模板,使用ART(Automatic Registration Toolbox)软件将群体空间的b=0图像非线性配准到ICBM-152模板,由此产生的ART变换在受试者间平均化构建最终HARDI脑模板,流程图如图 4所示.
|
图 4 HARDI脑模板构建流程图 Figure 4 Flow chart of constructing HARDI brain template |
张量重定向技术的出现[37]使得DTI数据集能够进行空间标准化,因此不同的DTI数据可以比较组间张量的方向数量[38].然而,DTI数据的空间标准化通常是将每个受试者的T1或者T2加权图像配准到一个模板空间,如ICBM-152模板,然后把相同的变换应用到相应的DTI数据或者选择一个受试者的DTI数据作为参考并把其他受试者的DTI数据配准到参考图像上.当标准化没有涉及张量信息时,研究者们不能保证受试者间的扩散特性是匹配的.此外,如果两个数据集没有达到空间匹配,那么基于不形变图像,如T1加权图像,估计的变换是不适合使用易形变的常规自旋回波-回波平面成像序列或者平行成像序列.同时,不同受试者间EPI-DTI数据呈现的伪影不同,空间标准化时伪影对于脑干、颞叶和额叶等脑区域影响较大.最后,当使用单个受试者的DTI数据作为参考时,需要考虑单个受试者的大脑不可能代表同一个成像组的其他受试者,且单个受试者的数据比平均多个数据集得到的模板具有更多的噪声,噪声会降低标准化的准确性和群体平均的有效性,限制了DTI脑模板的临床应用潜力.因此,一个具有代表性的高分辨率人脑扩散张量模板对于群体神经元结构完整性和连通性具有重要价值.
人脑的高分辨率扩散张量模板比目前可用的DTI模板更能代表平均脑微观结构,可以用来作为不同受试者DTI数据集空间标准化的参考标准;其次高分辨率人脑扩散张量模板可以与概率纤维追踪相结合构建出人脑白质的概率图谱;另外,构建高分辨率扩散张量脑模板所用的方法可以对患者和健康对照组间的临床数据进行组间比较,分析找出两者间的微小差异,对于脑疾病的研究具有重要价值,因此人脑高分辨率扩散张量模板的发展对于神经影像至关重要.
Q空间微分同胚重建方法是构建高分辨率扩散张量脑模板的方法之一,这是一种简单且适用范围广泛的扩散采样方案,包括单壳即高角度扩散分辨率成像、多壳和网格采样方案即DSI采样,这使得未来的研究可以充分利用网格采样或多壳采样方案.此外,Q空间微分同胚的重建方法可以应用于任何满足微分同胚空间变换方法,包括刚体变换、仿射变换和非线性变换.但是Q空间微分同胚重建仍存在局限性,微分同胚映射需要映射函数具有反函数,且反函数是可微的.在实践中,反函数的存在意味着主体和模板之间应该有一对一的结构映射,这不是普遍适用的.例如,受试者由于肿瘤或血肿有病理变化可能不符合微分同胚的重建,因为它不满足一对一的要求.
相比于Q空间微分同胚重建方法,基于HARDI构建的人脑扩散张量模板具有更高的图像清晰度,其图像伪影更少,能够区分较小的白质纤维束.不过,由于受试者个体特征性和参考空间选定以及体素大小的原因,该方法在当下更全面的定量分析中是存在问题的.
目前被广泛应用的脑模板大多是基于西方群体样本构建而来的,然而由于中西方人脑在大小和形态上具有较大的差异性,此类脑模板用于脑成像的研究准确性欠佳,因此本课题组前期构建了基于磁共振图像的中国人脑模板.该模板能够精确呈现出脑部细节解剖结构,为脑结构和功能评估分析提供了一个标准空间[39].此外,本课题组[40]还提出了基于多项式展开模型的DTI图像配准算法,采用详细的张量重新定位策略校准扩散张量,并对评价指标进行了对比试验,结果表明该算法具有快速的收敛性以及较高的配准度.近期,随着基于大脑模板的MRI扫描自动定位方法[41]的不断改进,对于单个受试者的多次扫描,一致的扫描定位有利于精确地追踪大脑结构随时间的变化,便于评估病情发展和治疗效果.另外,磁共振图像通常由于较长的扫描时间而导致磁共振扫描易受伪影的影响,为了加快扫描速度,提高扫描效率,近些年并行成像技术和压缩感知技术成为研究热点,研究者们通过结合并行成像和压缩感知技术,能够在快速成像的同时有效减少图像伪影,保留图像细节[42, 43].然而构建扩散张量脑模板进行数据预处理时需要提取脑实质,基于阈值分割的脑实质提取(Brain Extraction Tool, BET)算法对于正常脑实质能够获得较快的分割效果,但是当受试者脑实质中出现病灶肿瘤时分割效果往往不理想.为了有利于HARDI模板的研究,未来我们将加快张量重新定位的速度,并探讨DTI配准中可能存在的其他问题,同时不断改进脑实质分割算法等.
| [1] | MAKRIS N, WORTH A J, SORENSEN A G, et al. Morphometry of in vivo human white matter association pathways with diffusion-weighted magnetic resonance imaging[J]. Ann Neurol, 2010, 42(6): 951-962. |
| [2] | SZESZKO P R, ARDEKANI B A, ASHTARI M, et al. White matter abnormalities in first-episode schizophrenia or schizoaffective disorder:a diffusion tensor imaging study[J]. Am J Psychiatry, 2005, 162(3): 602-605. DOI: 10.1176/appi.ajp.162.3.602. |
| [3] | BRUNO S, CERCIGNANI M, RON M A. White matter abnormalities in bipolar disorder:a voxel-based diffusion tensor imaging study[J]. Bipolar Disord, 2008, 10(4): 460-468. DOI: 10.1111/j.1399-5618.2007.00552.x. |
| [4] | OZSUNAR Y, GRANT P E, HUISMAN T A, et al. Evolution of water diffusion and anisotropy in hyperacute stroke:significant correlation between fractional anisotropy and T2[J]. AJNR Am J Neuroradiol, 2004, 25(5): 699-705. |
| [5] | ARFANAKIS K, GUI M, TAMHANE A A, et al. Investigating the medial temporal lobe in Alzheimer's disease and mild cognitive impairment, with Turboprop diffusion tensor imaging, MRI-volumetry, and T2-relaxometry[J]. Brain Imaging Behav, 2007, 1(1): 11-21. |
| [6] | ARFANAKIS K, HAUGHTON V M, CAREW J D, et al. Diffusion tensor MR imaging in diffuse axonal injury[J]. AJNR Am J Neuroradiol, 2002, 23(5): 794-802. |
| [7] | GROSS D W. Diffusion tensor imaging in temporal lobe epilepsy[J]. Epilepsia, 2011, 52(s4): 32-34. |
| [8] | KLINGBERG T. Microstructure of temporo-parietal white matter as a basis for reading ability:evidence from DTI[J]. Eur Psychiat, 2002, 17(Suppl 1): 48. |
| [9] | VARENTSOVA A, ZHANG S, ARFANAKIS K. Development of a high angular resolution diffusion imaging human brain template[J]. Neuroimage, 2014, 91(2): 177-186. |
| [10] | BASSER P J, PIERPAOLI C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI[J]. J Magn Reson, 2011, 213(2): 560-570. DOI: 10.1016/j.jmr.2011.09.022. |
| [11] | JONES D K, GRIFFIN L D, ALEXANDER D C, et al. Spatial normalization and averaging of diffusion tensor MRI data sets[J]. Neuroimage, 2002, 17(2): 592-617. DOI: 10.1006/nimg.2002.1148. |
| [12] | GREVE D N, FISCHL B. Accurate and robust brain image alignment using boundary-based registration[J]. Neuroimage, 2009, 48(1): 63-72. DOI: 10.1016/j.neuroimage.2009.06.060. |
| [13] | PARK H J, KUBICKI M, SHENTON M E, et al. Spatial normalization of diffusion tensor MRI using multiple channels[J]. Neuroimage, 2003, 20(4): 1995-2009. DOI: 10.1016/j.neuroimage.2003.08.008. |
| [14] | ZHANG H, YUSHKEVICH P A, GEE J C. Deformable registration of diffusion tensor MR images with explicit orientation optimization[J]. Med Image Comput Assist Interv, 2005, 8(1): 172-179. |
| [15] | M LLER H P, UNRATH A, LUDOLPH A C, et al. Preservation of diffusion tensor properties during spatial normalization by use of tensor imaging and fibre tracking on a normal brain database[J]. Phys Med Biol, 2007, 52(6): N99-N109. DOI: 10.1088/0031-9155/52/6/N01. |
| [16] | ZHANG S, CAREW J D, ARFANAKIS K. Variability of diffusion tensor characteristics in human brain templates: effect of the number of subjects used for the development of the templates[C]. ISMRM Annual Meeting Proceedings, 2010. |
| [17] | MORI S, OIHI K, JIANG H Y, et al. Stereotaxic white matter atlas based on diffusion tensor imaging in an icbm template[J]. Neuroimage, 2008, 40(2): 570-582. DOI: 10.1016/j.neuroimage.2007.12.035. |
| [18] | WOODS R P, GRAFTON S T, HOLMES C J, et al. Automated image registration:i. general methods and intrasubject, intramodality validation[J]. J Comput Assist Tomo, 1998, 22(1): 139-152. DOI: 10.1097/00004728-199801000-00027. |
| [19] | BLOKLAND G A, DE ZUBICARAY G I, MCMAHON K L, et al. Genetic and environmental influences on neuroimaging phenotypes:a meta-analytical perspective on twin imaging studies[J]. Twin Res Hum Genet, 2012, 15(3): 351-371. DOI: 10.1017/thg.2012.11. |
| [20] | JAHANSHAD N, KOHANNIM O, TOGA A W, et al. Diffusion imaging protocol effects on genetic associations[J]. Proc IEEE Int Symp Biomed Imaging, 2012, 88(1): 944-947. |
| [21] | JAHANSHAD N, KOCHUNOV P V, SPROOTEN E, et al. Multi-site genetic analysis of diffusion images and voxelwise heritability analysis:A pilot project of the ENIGMA-DTI working group[J]. Neuroimage, 2013, 81(11): 455-469. |
| [22] | JENKINSON M, BANNISTER P, BRADY M, et al. Improved optimization for the robust and accurate linear registration and motion correction of brain images[J]. Neuroimage, 2002, 17(2): 825-841. DOI: 10.1006/nimg.2002.1132. |
| [23] | KOCHUNOV P, LANCASTER J L, THOMPSON P, et al. Regional spatial normalization:toward an optimal target[J]. J Comput Assist Tomo, 2001, 25(5): 805-816. DOI: 10.1097/00004728-200109000-00023. |
| [24] | KOCHUNOV P, LANCASTER J, THOMPSON P, et al. An optimized individual target brain in the Talairach coordinate system[J]. Neuroimage, 2002, 17(2): 922-927. DOI: 10.1006/nimg.2002.1084. |
| [25] | PENG H L, ORLICHENKO A, DAWE R J, et al. Development of a human brain diffusion tensor template[J]. Neuroimage, 2009, 46(4): 967-980. DOI: 10.1016/j.neuroimage.2009.03.046. |
| [26] | GUI M Z, PENG H L, CAREW J D, et al. A tractography comparison between turboprop and spin-echo echo-planar diffusion tensor imaging[J]. Neuroimage, 2008, 42(4): 1451-1462. DOI: 10.1016/j.neuroimage.2008.05.066. |
| [27] | ZHANG S W, PENG H L, DAWE R J, et al. Enhanced ICBM diffusion tensor template of the human brain[J]. Neuroimage, 2011, 54(2): 974-984. DOI: 10.1016/j.neuroimage.2010.09.008. |
| [28] | BASSER P J, MATTIELLO J, LEBIHAN D. Estimation of the effective self-diffusion tensor from the NMR spin echo[J]. J Magn Reson, 1994, 103(3): 247-252. DOI: 10.1006/jmrb.1994.1037. |
| [29] | JEURISSEN B, LEEMANS A, TOURNIER J D, et al. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging[J]. Hum Brain Mapp, 2013, 34(11): 2747-2766. DOI: 10.1002/hbm.22099. |
| [30] | WEDEEN V J, HAGMANN P, TSENG W Y I, et al. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging[J]. Magn Reson Med, 2005, 54(6): 1377-1386. DOI: 10.1002/(ISSN)1522-2594. |
| [31] | YEH F C, TSENG W Y. NTU-90:a high angular resolution brain atlas constructed by q-space diffeomorphic reconstruction[J]. Neuroimage, 2011, 58(1): 91-99. DOI: 10.1016/j.neuroimage.2011.06.021. |
| [32] | HSU Y C, HSU C H, TSENG W Y. Correction for susceptibility-induced distortion in echo-planar imaging using field maps and model-based point spread function[J]. IEEE Trans Med Imaging, 2009, 28(11): 1850-1857. DOI: 10.1109/TMI.2009.2026474. |
| [33] | HSU Y C, LO Y C, CHEN Y J, et al. NTU-DSI-122:A diffusion spectrum imaging template with high anatomical matching to the ICBM-152 space[J]. Hum Brain Mapp, 2015, 36(9): 3528-3541. DOI: 10.1002/hbm.22860. |
| [34] | ALEXANDER D C, BARKER G J, ARRIDGE S R. Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data[J]. Magn Reson Med, 2002, 48(2): 331-340. DOI: 10.1002/(ISSN)1522-2594. |
| [35] | TUCH D S, REESE T G, WIEGELL M R, et al. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity[J]. Magn Reson Med, 2002, 48(4): 577-582. DOI: 10.1002/(ISSN)1522-2594. |
| [36] | HASAN K M, KAMALI A, KRAMER L A, et al. Diffusion tensor quantification of the human midsagittal corpus callosum subdivisions across the lifespan[J]. Brain Res, 2008, 1227(3): 52-67. |
| [37] | ALEXANDER D C, PIERPAOLI C, BASSER P J, et al. Spatial transformations of diffusion tensor magnetic resonance images[J]. IEEE Trans Med Imaging, 2001, 20(11): 1131-1139. DOI: 10.1109/42.963816. |
| [38] | SCHWARTZMAN A, DOUGHERTY R F, TAYLOR J E. Cross-subject comparison of principal diffusion direction maps[J]. Magn Reson Med, 2005, 53(6): 1423-1431. DOI: 10.1002/(ISSN)1522-2594. |
| [39] |
LI J, JIANG F, WEI L, et al. Magnetic resonance image-based Chinese brain template construction[J].
Chinese Journal of Medical Physics, 2017, 34(6): 614-618.
李均, 蒋帆, 魏乐, 等. 基于磁共振图像构建中国人脑模板[J]. 中国医学物理学杂志, 2017, 34(6): 614-618. DOI: 10.3969/j.issn.1005-202X.2017.06.015. |
| [40] | WANG Y J, CHEN Z G, NIE S D, et al. Diffusion tensor image registration using polynomial expansion[J]. Phys Med Biol, 2013, 58(17): 6029-6046. DOI: 10.1088/0031-9155/58/17/6029. |
| [41] |
YAN X, ZHOU M X, YANG G, et al. A brain atlas based automatic localization method for MRI[J].
Chinese J Magn Reson, 2014(2): 196-205.
严序, 周敏雄, 杨光, 等. 基于大脑模板的MRI扫描自动定位方法[J]. 波谱学杂志, 2014(2): 196-205. DOI: 10.3969/j.issn.1000-4556.2014.02.006. |
| [42] |
HUANG L J, SONG Y, ZHAO X C, et al. A new combination scheme of GRAPPA and compressed sensing for accelerated magnetic resonance imaging[J].
Chinese J Magn Reson, 2018, 35(1): 31-39.
黄丽洁, 宋阳, 赵献策, 等. 一种结合并行成像和压缩感知的快速磁共振成像新方法[J]. 波谱学杂志, 2018, 35(1): 31-39. |
| [43] |
GAO M, XIE H B, LI Z M, et al. A synchronized compressed sensing scan-reconstruction scheme in magnetic resonance imaging[J].
Chinese J Magn Reson, 2016, 33(2): 257-268.
高芒, 谢海滨, 李智敏, 等. 压缩感知同步扫描重建及其采样方案的研究[J]. 波谱学杂志, 2016, 33(2): 257-268. |
 2018, Vol. 35
2018, Vol. 35 
