引言

磁共振成像（MRI）作为现代医学重要的成像技术，具有可任意层面成像、无电离辐射、成像参数多，以及对软组织分辨率高等诸多优点^[1].在成像过程中，样品的空间位置信息是通过梯度磁场对样品空间的编码获得，因此，磁共振图像质量与梯度系统性能密切相关.梯度系统一般包括梯度波形发生器、梯度功率放大器、梯度线圈，以及梯度涡流补偿模块.当变化的电流通过梯度线圈时，由于涡流效应，会引起样品空间的梯度场失真，在图像上产生涡流伪影.在MRI系统设计中，一般采用梯度预加重模块实现涡流的补偿.早期梯度预加重模块由模拟电路实现^[2]，近年来，随着数字电路技术的发展，采用数字电路实现梯度预加重模块，可以把梯度预加重模块集成至梯度波形发生器的数字信号处理器（DSP）或者现场可编程门阵列（FPGA）芯片中，不仅大大简化了系统设计，而且提高了系统性能^[3-5].

在MRI系统中，空间编码包含相位、频率和选层三个方向的梯度^[6]，每个方向上梯度需要多组补偿电流才能实现较好的补偿效果，所以在预加重模块中需要较多的计算单元计算补偿电流.为了实现更高的成像质量和更快的成像速度，MRI系统需要更多的补偿通道和补偿参数对涡流实现更加精确的补偿.预加重模块中这些计算单元的大量使用使FPGA设计面临巨大的压力.

在实际的MRI系统中，梯度信号的数据更新时间为微秒（μs）级，而FPGA可以实现纳秒（ns）级别的运算.所以本文提出了一种基于分时复用技术的梯度预加重模块设计方案，大大降低了梯度预加重模块的资源消耗，为现代MRI系统尤其是高场MRI系统的涡流高精度补偿提供了有效的解决方案.

1 方案设计

MRI系统样品空间的梯度磁场是由梯度线圈中的电流产生的，Biot-Savart定律中

$ B=\int_{L}{\frac{{{\mu }_{0}}I}{4\pi }}\frac{\text{d}l}{{{r}^{2}}} $

(1)

Idl为电流元，r为距离电流元的距离.由(1)式可知梯度磁场B与梯度电流I呈正比关系，(1)式对时间（t）微分可知磁场变化率也和电流变化率呈正比的关系.

$ \frac{\text{d}B}{\text{d}t}=\int_{L}{\frac{{{\mu }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}}\frac{\text{d}l}{{{r}^{2}}}\frac{\text{d}I}{\text{d}t} $

(2)

(2) 式说明，当梯度线圈中梯度电流快速切换时，会引起梯度磁场的快速变化.快速变化的梯度磁场使磁体内线圈的磁通量发生改变.由法拉第电磁感应定律中

$ E=-\frac{\text{d}\Phi }{\text{d}t}=-\frac{\text{d}\int_{s}{B}\cdot \text{d}s}{\text{d}t}=-\frac{\text{d}B}{\text{d}t}\cdot \int_{s}{\text{d}s} $

(3)

Φ为磁通量，s为磁通量有效面积，E为感应电动势.由(2)式可知，样品空间附近的导体在变化的磁场中会产生感应电流（涡流，eddy current），且感应电流强度与磁场变化率呈正比.涡流也会在样品空间产生磁场（涡流场），使样品空间的梯度磁场失真，从而影响空间编码，造成涡流伪影.涡流场的大小和涡流大小呈正比.

以LR电路模型分析MRI系统中的涡流形式，发现涡流${{i}_{e}}(t)$满足随时间衰减的多组e指数的叠加形式^[7]：

$ {{i}_{e}}(t)=\sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{\text{e}}^{-\frac{t}{{{\tau }_{i}}}}}} $

(4)

其中，${{\alpha }_{i}}$为涡流的幅度常数；${{\tau }_{i}}$为涡流衰减的时间常数，定义为涡流衰减至初始值37%时的时间；N为多组涡流组分的总组数，以下标i区分不同的涡流组分.

把整个MRI的梯度系统看作一个线性时不变系统^[8]，梯度波形发生器产生梯度信号到梯度线圈上产生实际电流的过程就是一种系统响应，可以得到梯度系统的传输函数：

$ {{H}^{sys}}(s)=\frac{{{I}^{sys}}(s)}{I(s)}=1-\sum\limits_{i=1}^{N}{\frac{{{\alpha }_{i}}s}{s+{{f}_{i}}}} $

(5)

(5) 式右边的第二项代表的就是产生涡流的部分.其中，${{I}^{sys}}$为梯度线圈输出的梯度电流的傅里叶变换；I为输入的梯度电流傅里叶变换；${{f}_{i}}$为和时间常数有关的分量，${{f}_{i}}=\frac{1}{{{\tau }_{i}}}$.由于补偿系统传输函数和梯度系统传输函数乘积为1，所以可以进一步得到理想补偿系统的传输函数${{H}^{cor}}(s)$和补偿后的梯度电流${{i}^{cor}}(t)$^[7]：

$ {{H}^{cor}}(s)=\frac{1}{{{H}^{sys}}(s)}=\frac{1}{1-\sum\limits_{i=1}^{N}{\frac{s\cdot {{a}_{i}}}{s+{{f}_{i}}}}}=1+\sum\limits_{i=1}^{N}{\frac{s\cdot {{a}_{i}}}{s+{{w}_{i}}}}, \quad {{w}_{i}}=\frac{1}{{{{{\tau }'}}_{i}}} $

(6)

$ {{i}^{cor}}(t)=1+\sum\limits_{i=1}^{N}{{{a}_{i}}{{\text{e}}^{-\frac{t}{{{{{\tau }'}}_{i}}}}}} $

(7)

${{a}_{i}}$是补偿电流的幅度常数，${{{\tau }'}_{i}}$是补偿电流的时间常数，同样，下标i区分不同的补偿组分.

用数字电路实现此系统，对(6)式和(7)式进行离散化处理，得到离散条件下补偿系统传输函数和输出电流在时域上的形式：

$ {{H}^{cor}}(z)=1+\sum\limits_{i=1}^{N}{\frac{(1-{{z}^{-1}})\cdot {{A}_{i}}}{1-{{W}_{i}}\cdot {{z}^{-1}}}}, \quad {{W}_{i}}={{\text{e}}^{-\frac{T}{{{{{\tau }'}}_{i}}}}} $

(8)

$ {{i}^{cor}}[n]=1+\sum\limits_{i=1}^{N}{{{A}_{i}}{{\text{e}}^{-\frac{nT}{{{{{\tau }'}}_{i}}}}}} $

(9)

(8) 式中求和项代表涡流补偿系统中所有补偿电流的计算单元.其中，n为离散化的时间变量，${{A}_{i}}$为第i组分补偿电流的幅度常数，${{W}_{i}}$为和时间常数相关的系数，z为离散变换之后自变量，那么单组的计算单元的差分方程为：

$ {{y}^{cor}}[n]=A\cdot (x[n]-x[n-1])+W\cdot {{y}^{cor}}[n-1], \quad W={{\text{e}}^{-\frac{T}{{{{{\tau }'}}_{{}}}}}} $

(10)

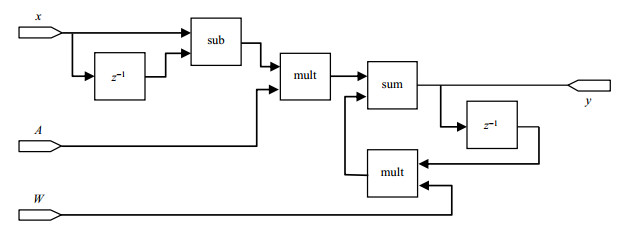
其中T是单组预加重模块中计算单元的采样周期，也是梯度预加重模块的数据更新时间；x为梯度电流输入；y为补偿后的梯度电流输出；A是补偿电流的幅度常数；W为和时间常数相关的系数.根据(10)式设计梯度预加重计算单元的硬件实现框图，如图 1所示.

把如图 1所示的计算单元输出的各组补偿电流与原本的梯度电流叠加，最终输出的就是补偿后的梯度电流.

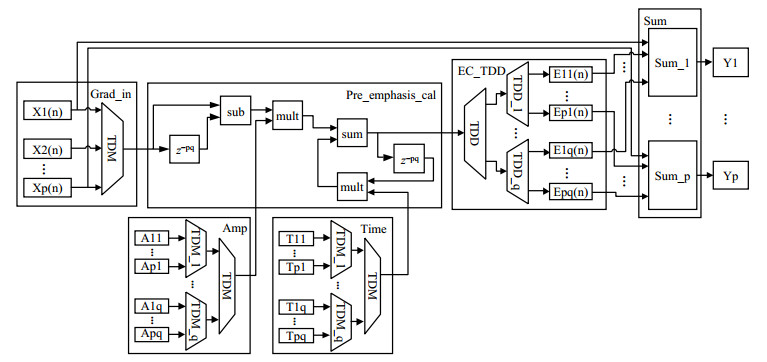
MRI梯度预加重模块的传统实现方案中每组补偿电流都对应一个预加重计算单元^[9].面对现代MRI系统的需求，这种实现方案会占用大量的逻辑资源，FPGA资源经常会很紧张.同时，以FPGA纳秒级别的运算速度处理微秒级别的梯度预加重数据计算对性能也是极大的浪费.采用分时复用的设计方法，使用一个计算单元分时计算出所有补偿电流（如图 2所示，图中p为补偿通道数，q为每个通道补偿参数的组数），提高N倍（N为所有补偿电流的组数，N=pq）的处理速度来节省N倍资源，这样既发挥了FPGA的计算性能的优势，又解决了FPGA资源紧张的问题.

分时复用功能由数据选择单元和数据分配单元共同实现.梯度数据和预加重参数通过数据选择单元一一对应地进入预加重计算单元，然后计算单元得到的结果输入到数据分配单元，实现各组梯度补偿数据和通道间的映射，相同通道的所有梯度补偿数据和原梯度数据求和得到最终补偿后的梯度数据.

由于信号进行分时传输，进入计算单元的数据不再具有连续性.原本计算单元同一组梯度补偿数据的相邻数据延迟为1个时钟周期，采用分时复用后，进入预加重计算单元的同一组梯度补偿数据相邻数据之间延迟p×q个时钟周期.因此，分时复用方案下的计算单元的差分方程如(11)式所示，和单组梯度预加重计算单元形式略有区别.

$ {{i}^{cor}}[n]=A\cdot (i[n]-i[n-pq])+W\cdot {{i}^{cor}}[n-pq], \quad W={{\text{e}}^{-\frac{pqT}{{{{{\tau }'}}_{{}}}}}} $

(11)

根据(11)式，将图 1所示的梯度预加重单元中的延迟${{z}^{-1}}$置为${{z}^{-pq}}$，即可实现复用方案下的梯度补偿数据计算.虽然计算单元的时钟频率增大到原来的p×q倍，但是每隔p×q个时钟周期，计算单元才完成一次同组补偿数据的数据更新，所以分时复用下梯度预加重模块的数据更新周期仍然保持不变.

2 FPGA实现

本文使用Xilinx公司的xc7a100tfgg676-2芯片实现梯度预加重模块的设计，并且完成梯度预加重模块和梯度波形发生器模块的系统集成.

2.1 方案实现

根据图 2及(11)式，在Matlab软件中搭建梯度预加重模型，然后转换成硬件描述语言（HDL）代码，在FPGA中实现梯度预加重模块，实现对X、Y、Z梯度，B₀和动态匀场等11个通道，每组通道4组参数的涡流补偿.使用分时复用器（TDM）和分时解复用器（TDD）分别实现数据选择功能和数据分配功能.由于不同数据的路径不尽相同，所以不同数据之间会有不同时钟周期的延时，为保证预加重模块中预加重参数、梯度信号和补偿信号之间的时序对应关系，需要添加Sync模块同步各路数据. Sync模块由多个不同级数的寄存器链组成，通过寄存器链实现不同时钟周期的延迟，从而达到同步各路数据的目的.

为满足成像过程中梯度磁场高速切换的需求，该梯度预加重模块使用1 MHz时钟作为梯度数据更新时钟，使用44 MHz时钟作为该模块计算单元的时钟进行补偿电流的计算.整个模块的输入到输出延迟为4 μs，梯度数据更新时间为1 μs.

梯度波形发生器使用AD5762实现梯度输出的数模转换. AD5762的数据转换精度为16 bit，所以计算单元的输入和输出数据的精度也设置为16 bit.幅度常数A表示各补偿组分的权重，采用16 bit二进制数表示幅度常数能精确到0.002%，完全满足区分各组分权重的精度要求.时间常数${\tau }'$存在于涡流计算公式的指数中[如(11)式所示]，由于FPGA进行指数运算十分不便，所以在上位机先完成$W={{\text{e}}^{-T/{\tau }'}}$的计算，然后把计算出的W转换成二进制数据发送给FPGA完成梯度预加重计算. MRI系统中涡流的时间常数一般在1~500 ms之间，对应的W范围是0.999 001~0.999 998，精度要求为10^-7，因此采用32 bit的二进制数量化W进行计算.

2.2 资源消耗

通过查看资源利用率报告，得到的两种设计方案的资源使用情况，如表 1所示：

表 1中总体资源是xc7a100tfgg676-2芯片的资源总量，由于梯度预加重模块和梯度波形发生器是集成在同一片FPGA上的，所以梯度预加重模块可用资源要少于总体资源.

实现分时复用功能的数据选择单元和数据分配单元需要消耗大量的寄存器，模块还需要额外的寄存器链同步梯度数据和预加重参数之间的对应时序，所以分时复用方案中寄存器消耗比较大. FPGA内部具有充足的寄存器资源，所以寄存器资源消耗增大可以接受.从表 1中可以看出LUT和DSP资源消耗都有不同程度的降低，尤其是DSP资源，只有传统方案资源消耗的1/44. FPGA内的DSP资源本来就十分有限，在传统设计方案下，使用xc7a100tfgg676-2芯片甚至无法满足更多通道和更多参数梯度预加重模块对DSP资源的需求.而采用分时复用的设计方案，使用一个计算单元就能完成多通道多参数的预加重计算，可以极大地节约FPGA中的DSP资源.由于分时复用方案是通过提升数据处理速度换取资源上的节约，所以只要FPGA芯片能够满足速度需求，就可以实现预加重通道和参数组数的扩展，而本模块计算单元中使用的44 MHz时钟远未达到FPGA计算性能的极限，所以本方案还可以支持更多通道和参数的扩展.

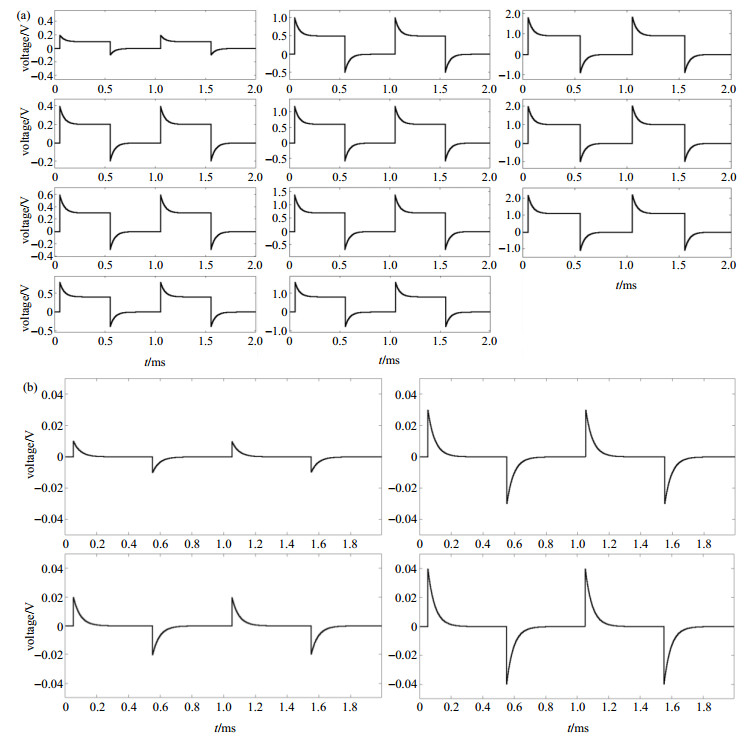
2.3 仿真及测试

在Matlab中通过仿真验证该分时复用模型的功能.以11组方波作为11路通道的输入，对每组通道设置不同的幅度常数和时间常数进行仿真，得到的仿真结果如图 3所示.可以看出，此模块可以完成11组通道4组参数梯度预加重的并行计算，产生合适的补偿电流.

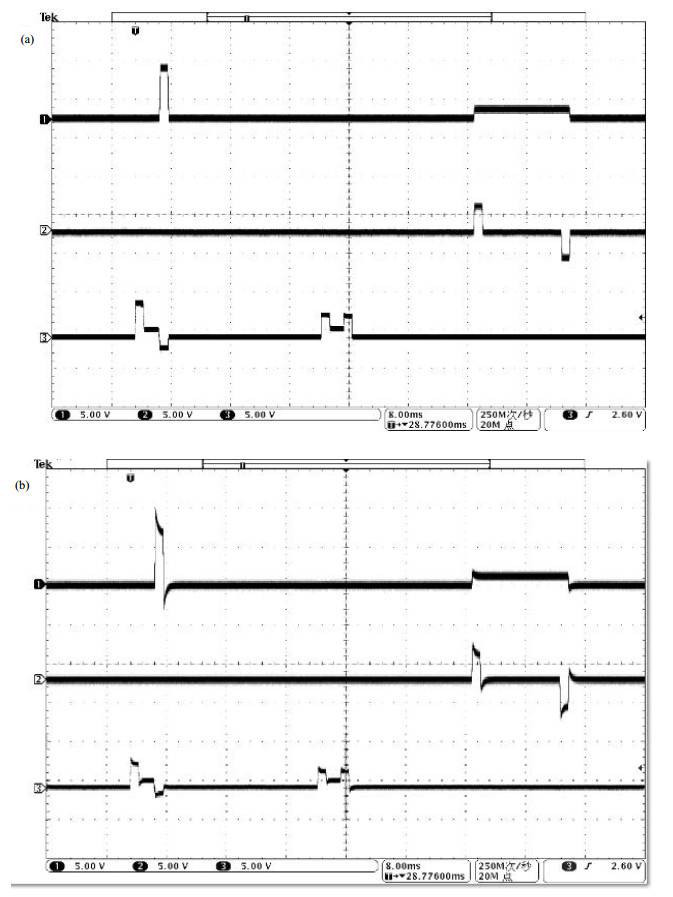
将此模块集成到梯度波形发生器中，并在自主研制的MRI控制台上测试梯度波形输出.使用多层面多回波（Multi-Slice Multi-Echo, MSME）序列进行测试，对X、Y、Z通道分别设置一组预加重参数，时间常数为0.2 ms，幅度常数为50%.使用Tektronix公司的MSO 4104B示波器测试MSME序列的梯度波形. 图 4所示的结果表明此模块能产生预期的梯度预加重效果，可以用于MRI系统的梯度涡流补偿.

3 实验与结果讨论

为验证本方案在MRI实验中对涡流的补偿效果，在0.35 T MRI扫描系统上进行两组实验^{[10, 11]}，第一组实验测定并补偿系统中的一阶涡流，第二组实验对比补偿前后图像.

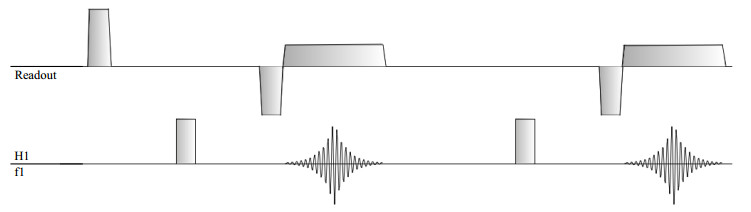
3.1 涡流曲线测定

通过谱相位间接测定涡流的方法^{[12, 13]}的序列如图 5所示.测试预加重前后涡流随时间变化的曲线，然后调试预加重参数，对比预加重前后涡流曲线，验证涡流补偿效果.实验样品为0.05 g/L的MnCl₂·4H₂O溶液，使用5 mm NMR样品管，内径为4 mm.实验参数如表 2所示.

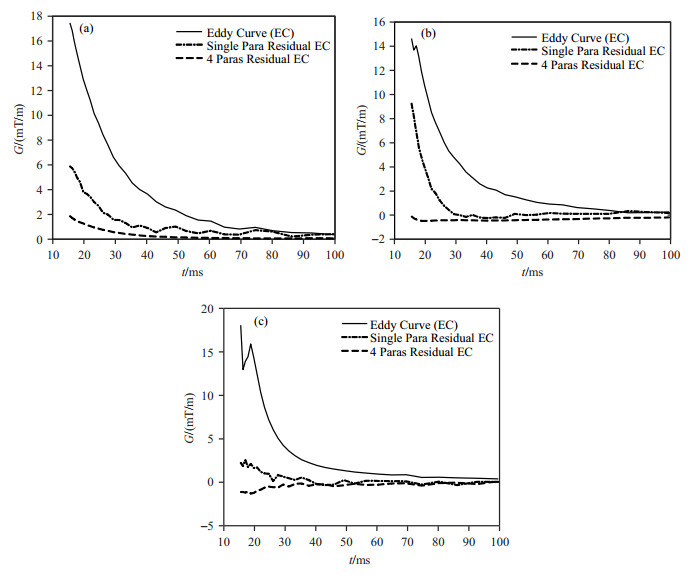
在以上实验条件下，测得X、Y、Z三个方向上的一阶涡流，对测得的涡流进行多指数拟合，利用奇异值分解（SVD）算法找到最优补偿参数，对MRI系统进行不同组数的预加重补偿，分别得到三个方向上补偿前涡流曲线、单组预加重补偿后残余的涡流曲线和4组预加重补偿后残余的涡流曲线，如图 6所示.

从实验结果中可以看出，经过不同组数的参数的梯度预加重补偿，系统中的涡流得到了不同程度的补偿，且4组参数梯度预加重的补偿效果明显优于单组参数梯度预加重.说明本方案极大地降低了0.35 T MRI系统中的涡流.

3.2 MRI实验

使用MSME序列采集磁共振图像，样品为0.05 g/L的MnCl₂·4H₂O溶液，使用5 mm NMR样品管.成像参数为：激发频率（SF）=14.922 MHz，视野（FOV）=10 mm×10 mm，谱宽（SW）=10 kHz，采样矩阵AcqMatrix=128×128，回波时间（TE）=25 ms，重复时间（TR）=2 000 ms.得到预加重前后图像如图 7所示.

图 7显示了预加重补偿前后的图像对比. 图 7(a)为预加重补偿前的图像，可以看出由于受涡流的影响，图像存在严重的伪影和模糊现象，有明显的形变；图 7(b)为加入预加重补偿之后的图像，其中伪影基本消除，图像轮廓清晰，无肉眼可见的形变，图像质量明显提高.

4 总结

针对现代MRI系统的多通道多参数梯度预加重模块资源消耗巨大的问题，本文提出了一种基于分时复用技术的梯度预加重模块设计方案，以提高数据处理速度换取较小的资源消耗，既节约了资源，又发挥了FPGA出色的计算性能.最后在0.35 T MRI系统上测量了预加重前后涡流曲线和MnCl₂·4H₂O溶液的图像，测试结果表明本方案极大地降低了涡流，显著改善了图像质量，取得了较好的涡流补偿效果.本设计为现代MRI系统的涡流精确补偿提供了理想的解决方案.