引言

在医学影像诊断领域，常常需要对患者影像数据和正常人体影像数据进行对比，或者对一组被研究的群体影像数据进行分析，从而发现两者或者一组影像数据个体间的差异^{[1, 2]}.图像配准是医学影像数据精确分析的基础，针对两幅医学图像的配准也就是传统的图像配准而言，通常指定一幅图像作为参考，如正常人体的影像数据，然后将另一幅图像变换到参考图像空间上，进而比较配准图像和参考图像之间的解剖结构差异.针对一组医学影像数据的配准也称为群体配准，群体配准的目的是为了精确分析一组影像数据的个体间差异^[3-5].为此研究者通常选取一幅具有较高群体代表性的图像作为参考，通过将其他图像配准到该选中的参考图像上完成群体图像的对比分析.这样选择代表性个体作为参考图像引导分析群体影像数据的做法可以减小引入个体偏差，但是无法避免个体偏差的引入，且人工选择的代表性个体有时并不是最好的.

寻找群体无偏的参考图像空间，完成群体配准和对比分析是解决这一问题的关键.一个非常重要的方法就是GroupMean方法，Joshi等人^[6]于2004年提出先将一组图像仿射配准到一个个体图像上，然后计算仿射配准的群体图像的算术平均，以算术平均图像为参考图像，再将所有仿射变换后的个体图像配准到算术平均图像上，并重新计算它们的算术平均图像，依次迭代，直到所有个体图像和算术平均图像所在空间基本一致为止.这一方法的理论基础是该组图像的算术平均接近于它们的群体中心，并且随着迭代次数的增加，算术平均图像会收敛于群体图像的中心^[7]，因而以算术平均图像的空间为参考空间，实现群体配准以及对比分析的偏差会越来越小.Geng等人^[8]于2009年基于所有图像间形变较小的假设进一步发展了GroupMean方法，使用线性弹性配准模型提出了无参考的群体配准方法.与此同时，也有很多研究者讨论了选取哪个个体图像作为参考使得群体配准的偏差最小^[9]、如何选取使得群体配准偏差最小的个体图像等^[10].

后来，研究者发现上述GroupMean方法通过计算群体图像算术平均引导群体配准，以迭代的方法收敛于群体图像中心的做法，存在很大不足^{[11, 12]}：算术平均后的图像过于平滑，这在迭代配准过程中，难以起到参考图像有效引导其它个体图像准确配准到参考图像空间的作用，因为参考图像本身就是比较模糊的，细节解剖结构不清楚.其次，GroupMean方法中起初假设所有个体图像都是仿射配准好的，在仿射配准阶段并没有解决选取哪个图像作为参考的问题.一些研究者以提高参考图像有效引导配准过程为目标，提出了增强算术平均图像锐化程度的方法，其中Wu等人^{[13, 14]}提出的SharpMean方法最具代表性，该方法选取一组图像中和所有个体图像的距离最小的作为初始参考图像，然后基于最小生成树算法将所有图像逐渐配准到参考图像空间^[15-18]，最后根据距离参考图像远近设定配准后的图像在下一轮参考图像创建中的权重系数，其中距离参考图像近的个体图像在下一轮参考图像构建中权重较大，反之则权重较小，这样构建的参考图像锐化程度得到了很大的提高，对于提高群体配准的准确性有较大帮助.

通过对目前主要群体配准方法的分析，我们发现SharpMean方法和GroupMean方法采用了一致的参考图像空间，即群体图像的算术平均图像所在空间来逼近群体图像的中心，其区别在于SharpMean方法采用的是加权算术平均，而GroupMean方法则直接采用了算术平均.以上两种方法都采取了迭代的算法流程，以期算术平均图像收敛到群体图像的中心，从而可以无限减小群体配准的偏差.事实上，在实际数值计算中，算术平均图像所代表的参考空间和群体图像的中心空间总是有差异的，无法达到群体配准的偏差最小.为此，本文基于群体图像所构成的拓扑空间的中心，提出一种偏差更小的群体图像配准方法.该群体配准方法的提出，可进一步降低群体配准的偏差，从而提高针对群体影像数据分析的精度，为临床疾病的影像学精准诊断提供帮助.

本文接下来先介绍群体配准主要方法的具体步骤，并详细阐述本文提出的基于拓扑中心的配准方法——TopologyCenter；然后对目前主要的两种群体配准方法和本文所提出的方法进行实验对比，通过对实验结果进行直观定量的分析阐述三种群体配准方法的差异；最后对当前群体配准问题的解决方法和本文所提出方法的优缺点进行讨论，并给出本文的结论.

1 方法 1.1 GroupMean方法

GroupMean群体配准方法^[6]及其后续发展方法是群体图像配准问题研究中非常重要的一类方法，在群体图像配准问题研究中占有重要的地位.假设${I_1}, {I_2}, \cdots , {I_N}$是一组群体图像，下面给出GroupMean方法的主要步骤.

Step1.把${I_1}, {I_2}, \cdots , {I_N}$仿射配准到一幅指定的参考图像上，仿射配准之后的群体图像仍记为${I_1}, {I_2}, \cdots , {I_N}$；

Step2.计算群体图像的算术平均图像${M^t} = \frac{1}{N}\left( {{I_1} + {I_2} + ... + {I_N}} \right)$，并令$t = 1$；

Step3.将${I_1}, {I_2}, \cdots , {I_N}$分别配准到M^t，得到配准后的群体图像$I_1^t, I_2^t, \cdots , I_N^t$；

Step4.计算新的群体图像算术平均${M^{t + 1}} = \frac{1}{N}(I_1^t + I_2^t + \cdots + I_N^t)$；

Step5.将$I_1^t, I_2^t, \cdots , I_N^t$分别配准到${M^{t + 1}}$，并令$t = t + 1$，重复上述两个步骤，直至t达到最高迭代次数程序停止.

1.2 SharpMean方法

上述GroupMean方法在每次迭代过程中，都需要计算一次群体图像的算术平均图像，会导致每次迭代配准过程的参考图像过于平滑，进而影响参考图像在配准过程中的有效引导作用，为此研究者提出加权平均生成群体平均图像的方法，同时基于群体图像特征提高加权平均图像的锐化度，来提高迭代配准过程中参考图像的有效引导，即SharpMean群体配准方法^{[13, 14]}，其主要步骤如下：

Step1.计算群体图像${I_1}, {I_2}, \cdots , {I_N}$的初始参考图像I_c，记初始群体平均图像${M^0} = {I_c}$，初始参考图像的选取按照该图像到群体图像距离之和最小的原则；

Step2.初始化权重、位移场函数和局部区域大小等参数，令t=1；

Step3.将群体图像${I_1}, {I_2}, \cdots , {I_N}$仿射配准到初始参考图像M⁰得到$I_1^t, I_2^t, \cdots , I_N^t$，并更新Step2.中的所有参数；

Step4.基于Step3.中仿射配准后更新的权重、位移场和局部区域参数计算群体平均图像M^t；

Step5.在图像集$I_1^t, I_2^t, \cdots , I_N^t, $M^t上按照群体图像之间的距离度量建立最小生成树路径；

Step6.将群体图像$I_1^t, I_2^t, \cdots , I_N^t$中每个图像按照最小生成树路径配准到群体平均图像M^t得到$I_1^{t + 1}, I_2^{t + 1}, \cdots , I_N^{t + 1}$；

Step7.更新当前权重、位移场和局部区域参数，并计算群体平均图像M^t+1；

Step8.让t=t+1重复上述Step5.~Step7.步骤，直至迭代计算停止.

SharpMean群体配准方法给出了一种初始参考图像的自动选取方法，在实现群体图像配准的过程中，采用了最小生成树的策略，使两两配准图像之间的形变较小，因而配准的精度有保障.基于图像距离加权的群体平均图像在每次迭代配准中作为参考图像，因其锐化程度较高.因此比GroupMean方法得到的过于平滑的群体算术平均图像更为合理.

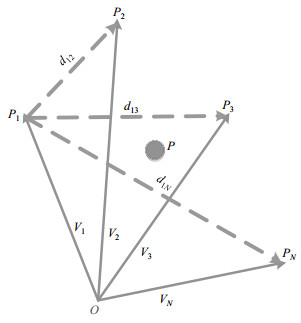
1.3 图像集拓扑中心定义

群体图像${I_1}, {I_2}, \cdots , {I_N}$的集合构成一个拓扑空间，在图 1中用拓扑空间的顶点${P_1}, {P_2}, \cdots , {P_N}$代表个体图像${I_1}, {I_2}, \cdots , {I_N}$，任意两个顶点之间的边用它们所代表的个体图像之间的两两配准位移场来表示，如d₁₂表示从图像I₁到I₂的配准位移场.下面给出拓扑中心P的定义，设点O为图像集拓扑空间的坐标原点，称$OP = \frac{1}{N}\sum\limits_{i = 1}^N {O{P_i}} $所确定的点P为空间${P_1}{P_2} \cdots {P_N}$的拓扑中心，拓扑中心P由群体图像共同确定，且是唯一存在的.

下面给出从顶点${P_1}, {P_2}, \cdots , {P_N}$到达拓扑中心P的路径推导，不妨以P₁为例，由于

$ OP = \frac{1}{N}\sum\limits_{i = 1}^N {O{P_i}} = O{P_1} + \frac{1}{N}\sum\limits_{i = 2}^N {(O{P_i} - O{P_1})} = O{P_1} + \frac{1}{N}\sum\limits_{i = 2}^N {{d_{1, i}}} , $

其中${d_{1, i}}$表示从图像I₁配准到图像I_i的配准位移场，这也就是说可以从图像I₁经过路径$\frac{1}{N}\sum\limits_{i = 2}^N {{d_{1, i}}} $到达拓扑中心.同理可有

$ OP = \frac{1}{N}\sum\limits_{i = 1}^N {O{P_i}} = O{P_i} + \frac{1}{N}\sum\limits_{j = 1(j \ne i)}^N {(O{P_j} - O{P_i})} = O{P_i} + \frac{1}{N}\sum\limits_{j = 1(j \ne i)}^N {d{}_{i, j}} , $

即从任一个体图像I_i可经路径$\frac{1}{N}\sum\limits_{j = 1(j \ne i)}^N {d{}_{i, j}} $到达拓扑中心P.综上所述，从任何一个个体图像都可以到达群体图像共同确定的拓扑中心P.

1.4 基于拓扑中心的群体配准方法TopologyCenter

根据1.3节中群体图像拓扑中心的定义，我们知道从群体图像中的任意个体图像都可以到达拓扑中心，且拓扑中心是由群体图像共同唯一确定的，基于此我们提出下面的群体图像配准方法.

Step1.将任一个体图像I_i配准到其他个体图像，得到配准位移场${d_{ij}}(j \ne i)$；

Step2.计算群体图像拓扑中心处的参考图像$I_i^{\rm{c}}(X) = {I_i}\left( {X{\rm{ + }}\frac{1}{N}\sum\limits_{j = 1(j \ne i)}^N {d{}_{i, j}} } \right)$，其中X为图像坐标；

Step3.将群体图像中其他个体图像逐个配准到参考图像$I_i^{\rm{c}}$，得到群体配准图像${I_1}^\prime , \cdots ,{I_{i - 1}}^\prime ,I_i^{\rm{c}},{I_{i + 1}}^\prime , \cdots ,{I_N}^\prime $.

事实上，我们也可以不厌其繁的将每个个体图像都按照Step1.和Step2.步骤逐个配准到拓扑中心，但是算法的计算量会很大，考虑到群体图像具有一定的共性，每个个体图像都有一致的解剖结构，因此该组群体图像中的个体图像都可以假设是拓扑同胚的，上述Step2.中计算的参考图像可以代表所有图像的拓扑中心位置解剖结构.

为评价群体配准图像相对于每个个体图像的偏差程度，我们提出群体配准的图像${I_1}^\prime ,{I_2}^\prime , \cdots ,{I_N}^\prime $偏向于某一个体图像I_i的累积偏差度量${\sigma _i} = \sum\limits_{j = 1}^N {H\left( {{I_j}^\prime ,{I_i}} \right)} $，其中${H\left( {{I_j}^\prime ,{I_i}} \right)}$表示群体配准后的图像${{I_j}^\prime }$相对于个体图像I_i的偏差，本文H采用互信息度量来计算图像${{I_j}^\prime }$偏向于I_i的程度.从两两对称配准的情况我们可以知道，群体拓扑中心相对于个体图像的偏差具有对称性，即拓扑中心相对于个体图像的偏差度量$H(I_i^{\rm{c}}, {I_j}){\rm{ }}(j = 1, 2, \cdots , N)$应具有最小的标准差.在本文实验中，我们将使用累积偏差和偏差标准差两个指标评价群体配准方法的性能.

作为群体图像配准的特殊情况，当N=2时，$OP = O{P_1} + \frac{1}{2}{d_{1, 2}} = O{P_2} + \frac{1}{2}{d_{2, 1}}$，此时将图像I₁，I₂分别配准到它们的中心位置P的方法称为两两对称配准.值得注意的是，当两两配准方法具有可逆性（${d_{1, 2}} = - {d_{2, 1}}$）时，我们无需计算两次配准位移场，因此，采用一种微分同胚的高精度的两两配准方法对群体图像配准至关重要，在本文中我们采用基于多项式展开的两两配准方法^{[19, 20]}，该方法具有极高的配准精度且对于单模态图像配准表现出微分同胚性.

2 实验方案与结果

本文基于群体图像拓扑中心，提出了群体配准方法TopologyCenter，并提出了直接衡量群体图像配准偏差的度量指标.在接下来的群体图像配准实验中，我们主要目的是验证所提出方法的有效性，并与当前两种群体配准方法GroupMean和SharpMean进行对比.

为了更好的对比三种群体配准方法的配准结果，我们选择以GroupMean和SharpMean方法的研究者公开的数据集为群体配准对象^[21].选择这一数据集的另一个好处是这两种方法的提出者开发了可视化的群体图像配准软件Glirt，并在软件中实现了GroupMean和SharpMean方法，因此基于Glirt软件和以上公开的数据集实现GroupMean和SharpMean群体配准是对这两种方法的较好实现.针对本文所提出的基于拓扑中心的群体图像配准方法，由于算法非常简捷无需设置很多参数，也不需要迭代计算，这里我们仅对该方法中使用的两两配准策略进行介绍.在我们前期提出的基于多项式展开的配准方法文献^{[19, 20]}中，建立了精确的仿射配准方法和非线性配准方法，并验证了先进行整体的仿射配准再进行非线性配准的策略可以很好的消除大变形后达到局部精确配准的目的，在本实验中我们仍然采用这一策略完成群体配准中的两两配准步骤.

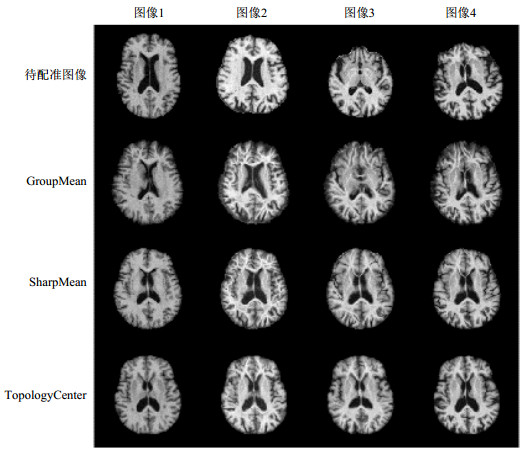
三种群体配准方法的实验结果如图 2所示.图 2第一行给出了公开数据集中四个个体图像的轴向中间层面图，四个个体图像矩阵大小都是204×204×162，从图像上可以看出四个个体图像之间的形变差异较大.图 2第二行和第三行分别是使用GroupMean方法和SharpMean方法的群体配准结果，从第二行可以看出，第一和第二个个体图像解剖结构大致对准，第三和第四个体图像并未达到与第一和第二个体图像准确配准，这可能是由于过于平滑的算术平均图像无法有效引导群体配准造成的.图 2第三行SharpMean方法的群体配准结果明显比优于GroupMean方法，四个个体图像较好的实现了精确配准，图像锐化程度高，解剖结构清晰可辨.图 2最后一行是使用本文提出的TopologyCenter群体配准方法对该公开数据集的配准结果，从图像上看我们方法的群体配准结果也非常好，个体图像都达到了准确配准，图像的锐化度与群体配准前的个体图像几乎没有差异，解剖结构清晰.

仅从上述图 2的群体配准实验结果中，我们无法衡量SharpMean方法和本文所提出的基于拓扑中心的TopologyCenter群体配准方法哪种更好，因为群体配准问题的研究没有金标准可以参考.下面我们通过计算群体配准图像和配准前个体图像间的累积偏差以及偏差标准差来定量的评价这两种方法的差异.表 1给出了三种群体配准方法的累积偏差和标准差计算结果，从累积偏差结果看，GroupMean、SharpMean和TopologyCenter三种方法结果都与第三个个体图像的累积偏差最小，这说明第三个个体图像配准前更接近于群体图像拓扑中心.从三种方法相对于四个个体图像中任一个体图像的累计偏差看，累积偏差都是GroupMean方法最大，SharpMean方法次之，TopologyCenter方法最小，这说明本文所提出的群体配准方法累积偏差最小.从三种方法相对于四个个体图像偏差的标准差看，GroupMean方法和SharpMean方法都大于TopologyCenter方法，并且只有TopologyCenter方法相对于四个个体图像的标准差值几乎相等，GroupMean和SharpMean方法相对于四个个体图像的标准差没有规律性，这说明本文所提出的基于拓扑中心的群体配准方法相对于个体图像具有群体对称性，GroupMean方法和SharpMean方法不具有群体对称性.

3 讨论与结论

本文在深入分析当前群体配准的主流方法GroupMean和SharpMean方法后，考虑到两种方法都是以迭代的方式用群体算术平均图像去逼近群体图像的中心，具有参考图像平滑、群体图像中心不明确等缺点，故通过分析群体图像的空间分布提出了基于拓扑中心的群体图像配准方法.通过严谨的理论论证，本文给出了群体图像拓扑中心的定义，明确了群体图像拓扑中心的唯一存在性，拓扑中心空间位置由所有个体图像共同决定.在此基础上，推导出了从任意个体图像到达群体图像拓扑中心的路径，并提出了基于拓扑中心的群体图像配准方法以及两两对称配准方法.针对群体配准问题的研究已经很多，但是尚没有直接衡量群体配准偏差的方法，本文给出了直接衡量群体配准偏差的度量指标累积偏差和偏差标准差，这对于群体图像配准问题的方法评价具有一定的意义.

为了与当前主流方法GroupMean和SharpMean群体配准方法进行非常精确的比较，我们基于SharpMean方法提出者所开发的Glirt软件和发布的公开数据集来实施三种方法的群体配准实验比较.实验结果表明，SharpMean方法和TopologyCenter方法群体配准结果好于GroupMean方法，在进一步的定量评价指标对比中，我们发现本文所提出的TopologyCenter群体配准方法比SharpMean方法具有更小的累积偏差，更重要的是TopologyCenter方法相对于各个个体图像的偏差呈现出群体对称性，这说明所提出的群体配准方法建立的拓扑中心空间能够更好的表达群体图像的共性解剖结构.

综上所述，本文基于群体图像的拓扑中心提出了一种新的群体图像配准方法——TopologyCenter，并直接衡量了群体配准相对于每个个体图像的偏差.实验结果表明，本文方法比当前两种主流方法对于个体图像的累积偏差和偏差标准差更小.在医学影像诊断领域，本文提出的群体配准方法可以帮助医生建立更客观的基于群体影像数据的模板参考图像，如基于正常人脑部影像数据的脑模板，可用来更精确的诊断脑部神经系统疾病；如医生需要根据大量同类型疾病的影像数据建立其共性特征库，也可以在本文群体配准的基础上进行，这样建立的特征将会更客观.