2. Department of Radiology, Weill Medical College of Cornell University, Ithaca, New York, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York, USA
2. Department of Radiology, Weill Medical College of Cornell University, Ithaca, New York, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York, USA
近年来,随着生活水平的提高和饮食结构的改变,脂肪肝的发生率呈明显上升趋势.脂肪肝虽为良性病变,但部分病例仍可发展为脂肪性肝炎、肝纤维化、肝硬化,甚至肝功能衰竭和肝细胞癌症,严重危害生命健康.早期诊断、及时治疗可使发生脂肪变性的肝细胞恢复正常,因此,采用无创性方法定量诊断脂肪肝在临床工作中具有非常重要的意义[1-4].
肝活检是目前临床评估肝脂肪含量的金标准,但这种方法具有侵入性,不是脂肪肝筛选、监测、临床决策或研究的最佳选择.超声(Ultra Sound,US)和计算机断层扫描(Computed Tomography,CT)检测技术分别通过间接的声像图和CT结果来反映脂肪肝的严重程度,可半定量评估肝脏内脂肪含量.但US检查质量和准确性取决于操作者、设备和患者因素,而且由于纤维化和炎症并存,严重脂肪肝变性患者US特征比较混杂.尽管CT可以精确观测X射线衰减值,但是脂肪以外的其他因素(如铁、铜、糖原、纤维化和水肿的存在)会影响X射线衰减值,导致其对轻中度脂肪变性不太敏感,脂肪定量不够准确;此外,CT还具有电离辐射,危害人体健康.磁共振(Magnetic Resonance, MR)技术可以把肝脏信号分解为独立的脂肪信号和水信号,因此将其用于评估肝脏脂肪比CT或US更客观直接[3, 5].相比于磁共振成像(MR Imaging,MRI),单体素质子磁共振波谱(1H Magnetic Resonance Spectroscopy,1H MRS)尽管一次扫描只能检测单个体素,但在测量肝脏脂肪含量方面主要具有如下优势:首先,它具有很宽的动态范围,能够检测任何范围的脂肪含量(0%~100%);其次,MRS非常敏感,能够检测治疗过程中肝脏甘油三酯含量的细微变化[6, 7];再者,它不受肝纤维化和铁沉积等混杂因素的影响[8, 9].
MRS定量肝脏脂肪含量可采用激励回波采集序列(Stimulated Echo Acquisition Mode,STEAM)和点分辨谱采集序列(Point-Resolved Spectroscopy Sequence,PRESS).相比PRESS序列,STEAM序列得到的结果更加稳定[10].近年来,基于STEAM开发的快速T2校正多回波波谱采集(High-Speed T2-Corrected Multi-Echo Acquisition,HISTO)序列,不仅缩短了回波时间(Echo Time, TE),减小了J耦合对结果的影响,同时也减少了病人需要屏气的时间,可以通过一次屏气获得一组不同TE的波谱数据,在脂肪肝临床检测方面更具优越性[11-15].
肝脏MRS数据采集完成后,需要对得到的数据进行后处理以获得质子密度脂肪分数(Proton Density Fat Fraction,PDFF).这类数据处理大多采用MRI扫描仪自带的处理软件,但一般模型比较简单,如有算法将化学位移大于δ 3.60的所有峰都看作水峰,因此得到的脂肪含量往往比实际结果要小[14].也可采用第三方软件如jMRUI(http://www.jmrui.eu/)进行处理,通过设置复杂的后处理模型和校正算法得到理想的结果,但其步骤繁琐,需要耗费大量的时间,而且具体处理过程需要人为主观判定,其结果受人为控制因素影响比较显著.本文首先开发了一种自动波谱后处理算法,该算法考虑了可能会使谱线失真扭曲的因素,并在算法内对全部谱线进行校准,排除了人为因素对结果产生的影响,同时通过精确划分水峰和脂肪峰确保了结果的准确性;然后,通过水脂模型和人体肝脏实验对算法的可行性和准确性进行了评估.
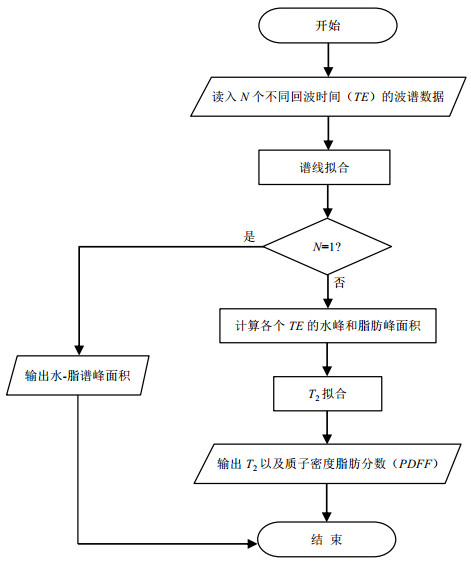
1 自动波谱后处理算法肝脏脂肪含量定量的自动波谱后处理算法如图 1所示,其流程如下:首先对读入的各个不同TE的波谱数据进行谱线拟合,得到每个谱的谱峰面积,然后对多个TE下的水和脂肪的谱峰面积进行T2拟合,得到水和脂肪在TE=0时的信号值,再计算得到最终的PDFF.
|
图 1 肝脏脂肪定量的自动波谱后处理算法流程图 Figure 1 Flow chart of automated spectral post-processing algorithm for liver fat quantification |
谱线拟合算法采用最小二乘法,通过设置谱峰形状并将所有谱峰的拟合幅值、半高宽和相位限定于一个特定区间内,对此区间进行局部寻优,通过不断迭代更新确定出最优解.
主磁场的不均匀性会导致感兴趣体素(Voxel of Interest, VOI)内质子共振频率展宽[16],因此采集到的谱峰实际上是高斯线型展宽的洛仑兹峰,在数学上可以用佛克脱(Voigt)线型表示[17, 18]:
| $ V(v) = \theta \cdot a \cdot {\rm{exp}}\left[ { - \frac{{4\ln 2{{(v - w)}^2}}}{{{u^2}}}} \right] + (1 - \theta ) \cdot a \cdot \frac{{{u^2}}}{{{{(v - w)}^2} + {u^2}}} $ | (1) |
其中变量v表示组分的化学位移,一个Voigt函数包括4个峰参数,分别为:a(峰高)、w(峰的中心频率)、u(峰的半高宽)、θ(高斯-洛仑兹系数).在这里,我们将所有谱峰都看作佛克脱线型.对于整个谱,利用(N+1)个峰进行拟合,其中N为脂肪峰的个数,1为水峰.根据相关文献[19]报道,脂肪信号可以用九个峰来模拟,即N=9.在此将脂肪峰亚甲基相对幅值置为1,其余各峰幅值按照文献所述比例等比缩减,用作后述算法相对初始值的估计.
化学位移限制:理论上水质子的化学位移在δ 4.70处,但考虑到主磁场的不均匀性,水质子的化学位移会在δ 4.70附近偏移.由于温度和个体差异等影响,脂肪峰亚甲基的化学位移也并不总是在δ 1.3处,因此,本算法首先从获得的谱上确定出水峰和脂肪峰亚甲基的化学位移,并固定脂肪峰之间的相对频率,从而得到其它脂肪峰的化学位移.确定水峰和脂肪峰亚甲基化学位移的方法如下:遍历化学位移δ 4.3~5.0范围,最大信号记为水质子的峰值;遍历化学位移δ 1.0~2.0范围,最大信号值记为脂肪峰亚甲基的幅值.通过上述定位出的水和脂肪峰亚甲基,反索引找到各自的化学位移.并将亚甲基峰的化学位移设置为δ 1.30,其它脂肪峰到最高脂肪峰之间相对化学位移如表 1所示[19].
| 表 1 脂肪多峰之间的相对化学位移和幅值 Table 1 Relative chemical shift (δ) and amplitude of fat peaks |
幅值限制:将上文中所确定的水峰最大值作为水峰的拟合初始值,将表 1中脂肪峰模型的相对幅值依次乘以亚甲基峰的幅值,作为各脂肪峰的拟合初始值.并将每个脂肪峰初始值的99%定为拟合的下限,上限则定为无穷大.
半高宽限制:以上文定出的水峰化学位移为中心向两边扩散,分别找到幅度为水峰幅值一半的数据点,通过这两个数据点的化学位移差算出水峰的半高宽△f:
| $ \mathit{\Delta }f = \gamma B \cdot ({\sigma _1} - {\sigma _2}) $ | (2) |
其中,γ为旋磁比,B代表外磁场强度,σ1和σ2分别表示水峰左右两边找到数据点所对应的化学位移.脂肪峰亚甲基的半高宽我们也用相同方法得出,其它脂肪峰的半高宽在亚甲基脂肪峰半高宽上下5 Hz之内寻优.
相位限制:相位校正是将自由感应衰减信号(Free Induction Decay, FID)经傅里叶变换后得到的实部和虚部采用下列公式进行混合:
| $ {R_i} = R_i^0 \cdot \cos ({\phi _i}) - I_i^0 \cdot \sin ({\phi _i}) $ | (3) |
| $ {I_i} = R_i^0 \cdot \sin ({\phi _i}) - I_i^0 \cdot \cos ({\phi _i}) $ | (4) |
其中Ri和Ii分别表示在相位谱中的第i个数据点的实部和虚部,Ri0和Ii0分别对应于无相位差的第i个数据点的实部和虚部,ϕi是第i个数据点处的相位.通常ϕi由两部分组成:与频率无关的部分和与频率线性相关的部分,可表述如下:
| $ {\phi _i} = {\phi _0} + \frac{i}{N} \cdot {\phi _1} $ | (5) |
其中ϕ0是零阶项,ϕ1是一阶项的常量,N是数据点的总数.
本文中相位校正采用全自动相位校准算法.纯吸收谱与存在相位差的谱相比具有一定的特征:(1)在纯吸收谱中,峰尾较短且对称,基线平坦;(2)纯吸收峰无负峰值.根据以上特征,相位校正方法分为“粗略校正”和“精细校正”[20, 21].
整个“粗略校正”过程分为三个步骤:首先,确定峰值的左右尾端位置;其次,利用峰的起始和结束之间的高度差来构造目标函数;最后,对构造的函数进行最小化,得到拟合谱线.目标函数(OF)定义为:
| $ OF = \sum\limits_{j = 1}^{PN} {abs} \left\{ {\sum\limits_{k = 0}^M {R[peak(j).Start - k] - } \sum\limits_{k = 0}^M {R[peak(j).End + k]} } \right\} $ | (6) |
其中R表示用(3)式和(4)式计算得到的波谱实部.peak(j).Start和peak(j).End表示识别到的第j个峰的起始点和结束点的位置.在本研究中,将识别峰的起始部分和结束部分(通常由几个点组成)分别设置为峰的左端和右端.M表示第j个识别峰的起始点(或结束点)的数目,用于计算高度差.一般情况下,M被设置为1≤M≤4,M>1是为了抑制噪声的影响.参数PN表示识别到的峰的个数.
虽然粗略校正后的波谱与吸收谱非常接近,但对于一些具有密集峰或其他一些有缺陷的复杂谱,仍可能存在轻微的相位偏差,因此需要对相位进行进一步的精细校正.在“精细校正”过程中,根据纯吸收峰无负峰值的特点,构造了一个新的惩罚函数PF,通过最小化自定义惩罚函数来进一步校正相位.为了构造出这种自定义的惩罚函数,将基线识别方法识别到的峰分为三类:正峰、负峰和畸变峰.首先,通过最大绝对值找出每个峰的峰值,并将其设置为这个峰值的高度.如果这个绝对值最大的点是正的,这个峰值初始化为正峰,否则它被初始化为负峰值.然后检查峰值中的每个点,如果在正峰中存在绝对值大于峰值高度10%的负点,则应将该峰值指定为畸变峰,同样,如果在负峰中有一些正点大于峰值高度的10%,则也应将该峰值设为畸变峰.如果大多数峰(>50%)为负,则将180°添加到ϕ0中.本文采用的惩罚函数PF定义为:
| $ PF = \sum\limits_{i = 1}^N {\{ TempR(i)} - abs[TempR(i)]{\} ^2} $ | (7) |
其中,
| $ TempR(i) = \left\{ \begin{array}{l} R(i), \;\;\;\;\;\;\;\;{\rm{正峰}}\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;{\rm{畸变峰}}\\ - R(i), \;\;\;\;\;{\rm{负峰}} \end{array} \right. $ | (8) |
N表示波谱数据点的个数,R表示数据的实部,根据峰值的特征计算临时谱TempR.若为正峰,临时谱的第i点的信号值与实谱中的对应点相同,但在畸变峰和负峰区域,点的值分别设置为0和对应点的相反数.(7)式的意义很简单:如果在临时谱中出现一个负点,我们将这个点的平方加到惩罚值上.
1.2 多回波拟合和质子密度脂肪分数计算通过谱峰拟合可以得到每个TE时谱线的总脂肪峰信号Mlipid和水峰信号Mwater.脂肪信号和水信号均会随着TE衰减,因此对此进行矫正是必不可少的步骤.为了得到TE=0时的水信号M0_water和脂肪信号M0_lipid、以及T2_water和T2_lipid,采用最小二乘法根据(9)式进行指数拟合:
| $ M(TE) = {M_0} \cdot {{\rm{e}}^{ - \frac{{TE}}{{{T_2}}}}} $ | (9) |
最后,脂肪分数PDFF采用下式计算得到:
| $ PDFF = \frac{{{M_{{\rm{0\_lipid}}}}}}{{{M_{{\rm{0\_lipid}}}} + {M_{{\rm{0\_water}}}}}} \cdot 100\% $ | (10) |
分别采用脂肪含量不同的水脂模型和肥胖志愿者对本文提出的全自动算法进行验证和评价.
水脂模型包含下述化学成分:水、植物油(初榨橄榄油)[22]、聚三梨醇酯80(TWEEN-80,表面活性剂,按油体积容量3%加入)、2 g/mL(w/v)琼脂.按油容积配比得到0%、10%、20%、30%、40%、60%、80%、100%共8组含油混合液,并将其放入离心管(内径25.98 mm,外径27.58 mm)[23-25].
共招募15名[男性13名,女性2名,平均年龄(33.8±12.3)岁]肥胖志愿者.在实验前确认所有被试均没有幽闭恐惧症、无金属植入物或起搏器等,被试均签署知情同意书.本研究通过华东师范大学人体伦理委员会批准.
2.2 MRI数据采集所有数据采集均在3 T MRI扫描仪(西门子MAGNETOM Prisma)上完成,采用体部线圈作为信号接收线圈.波谱数据采集采用HISTO序列.
水脂模型扫描参数如下:重复时间(TR)=3 000 ms,混合时间(TM)=10 ms,回波时间(TE)=12、24、36、48和72 ms,平均次数=4,带宽=1 200 Hz,采样点数=1 024,VOI大小为10*10*10 mm3.
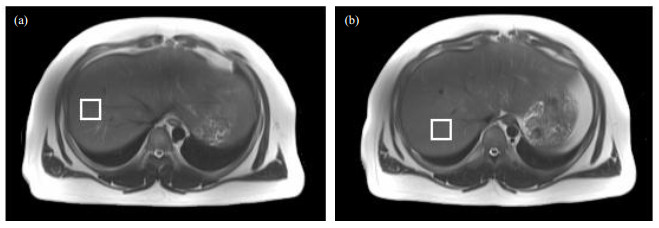
人体肝脏扫描参数如下:TR=3 000 ms,TM=10 ms,TE=12、24、36、48和72 ms,平均次数=1,带宽=1 200 Hz,采样点数=1 024,VOI大小为30*30*30 mm3.每个被试肝脏选取两个不同位置的VOI(图 2).借助T1加权定位像,将VOI定位在肝脏右叶,定位时避开肝脏边缘皮下脂肪以及大的胆道和血管结构,未设置空间预饱和带.每个VOI的MRS扫描持续时间为15 s,被试在一次屏气中完成.
|
图 2 同一被试的两个肝脏磁共振波谱感兴趣体素定位图.(a)第一个感兴趣体素定位;(b)第二个感兴趣体素定位 Figure 2 Two voxels of interest (VOIs) for liver MR spectra from the same subject. (a) The first VOI; (b) The second VOI |
本文提出的全自动后处理算法在MATLAB R2014b上实现.获得的MRS均采用本文提出的全自动后处理算法进行处理.作为对比,MRS数据同时也采用jMRUI5.2频谱分析软件包和西门子MRI扫描仪自带的Syngo后处理软件进行了处理.
jMRUI数据处理主要包含如下几个重要步骤:(1)将水峰的化学位移设置为δ 4.70;(2)采用九个脂肪峰模型拟合(表 1),将其它脂肪峰相对于脂肪峰亚甲基幅值比例固定;(3)由于水模数据用高斯峰拟合残差小,而人体肝脏数据用洛仑兹峰拟合残差小,所以水模和人体肝脏分别采用高斯函数和洛仑兹函数拟合;(4)脂肪峰亚甲基和水峰的线宽范围给定(具体范围因个体及匀场情况而异),其它脂肪峰的线宽和亚甲基峰范围相同.
2.4 数据分析采用IBM SPSS Statistics 23软件进行统计分析.将使用本文提出的全自动后处理算法得到的PDFF分别与西门子MRI扫描仪自带的Syngo处理软件和jMRUI软件包得到的PDFF作线性回归分析以及Bland-Altman一致性分析.将全自动后处理算法得到的水质子和脂肪质子的T2值分别与Syngo软件和jMRUI软件包处理得到的T2值进行配对t检验,分析其差异性.值得注意的是,由于脂肪含量很低时得到的T2误差较大,所以jMRUI测量得到PDFF < 2%的肝脏数据不参与T2的配对t检验.
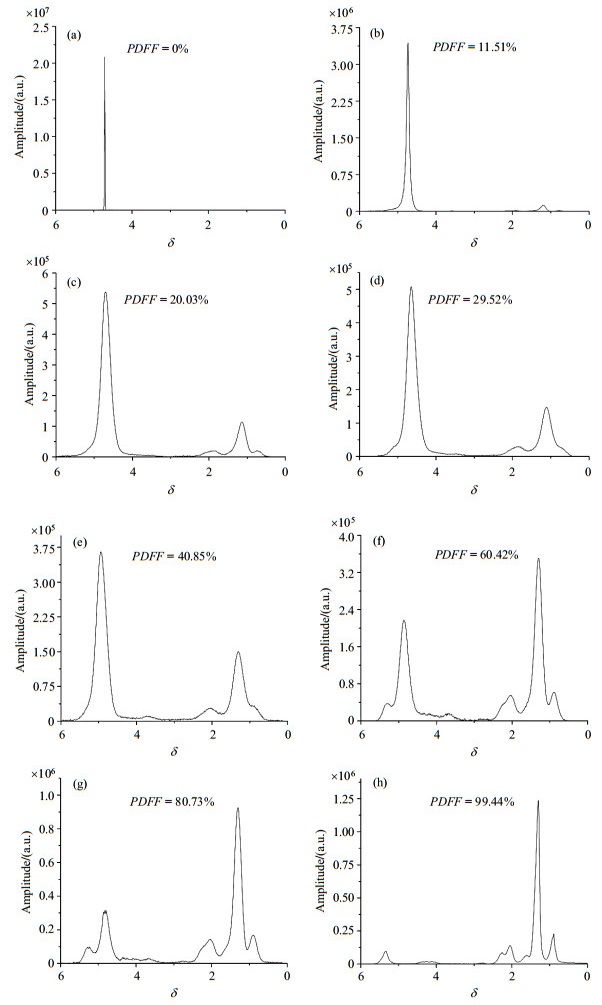
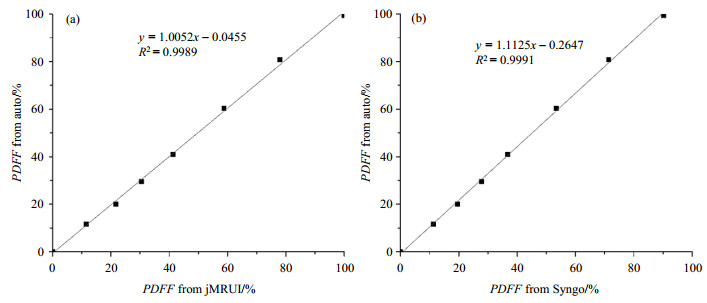
3 结果与讨论 3.1 体外水脂模型实验图 3为脂肪浓度不同的水脂模型在TE=12 ms的谱图以及通过全自动后算法得到的PDFF值,图 3(a)~(h)分别对应于脂肪容积比为0%、10%、20%、30%、40%、60%、80%、100%共8组含油混合液.图 4显示了全自动后处理算法(图、表中简写为auto)分别与jMRUI软件以及西门子MRI扫描仪自带的Syngo软件处理得到的PDFF的线性回归分析.结果显示全自动后处理算法得到的PDFF与jMRUI得到的结果高度一致,线性回归方程为
|
图 3 不同脂肪浓度的水模在TE=12 ms的磁共振波谱. (a)~(h)分别为脂肪容积比为0%、10%、20%、30%、40%、60%、80%和100%的8组含油混合液 Figure 3 MR spectra of the fat-water phantoms with various fat concentrations at TE=12 ms. (a)~(h) denote a mixed solution with an oil concentration of 0%, 10%, 20%, 30%, 40%, 60%, 80% and 100%, respectively |
|
图 4 水脂模型PDFF测量结果对比. (a)自动后处理算法与jMRUI软件得到的PDFF线性回归分析;(b)自动后处理算法与西门子Syngo软件得到的PDFF线性回归分析 Figure 4 Comparison of measured PDFF values in fat-water phantoms. (a) Linear regression analysis between the automated post-processing algorithm and jMRUI software; (b) Linear regression analysis between the automated post-processing algorithm and Siemens Syngo software |
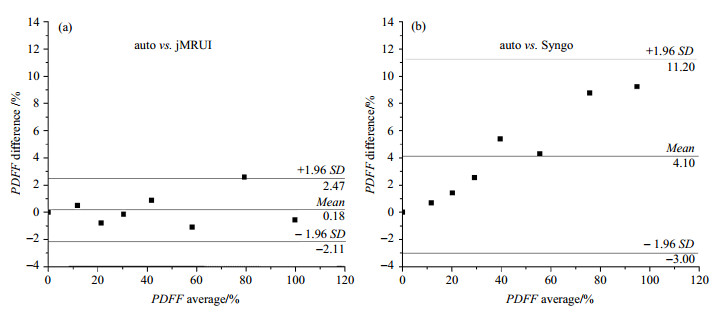
|
图 5 水脂模型不同后处理方法得到的PDFF的Bland-Altman分析 Figure 5 Bland-Altman analysis for the PDFFmeasurements with various post-processing methods in fat-water phantoms |
| 表 2 水脂模型自动后处理算法、jMRUI软件以及西门子Syngo软件处理得到的脂肪质子和水质子的T2值 Table 2 T2 values of water and fat in fat-water phantoms obtained from automated post-processing algorithm, jMRUI software and Siemens Syngo software |
图 6为不同脂肪含量的人体肝脏在TE=12 ms时的谱图以及通过自动后处理算法得到的PDFF值.图 7显示了自动后处理算法分别与jMRUI软件以及Syngo软件处理得到的PDFF的线性回归分析结果:自动后处理算法得到的PDFF与jMRUI得到的结果呈线性回归关系,线性回归方程为:
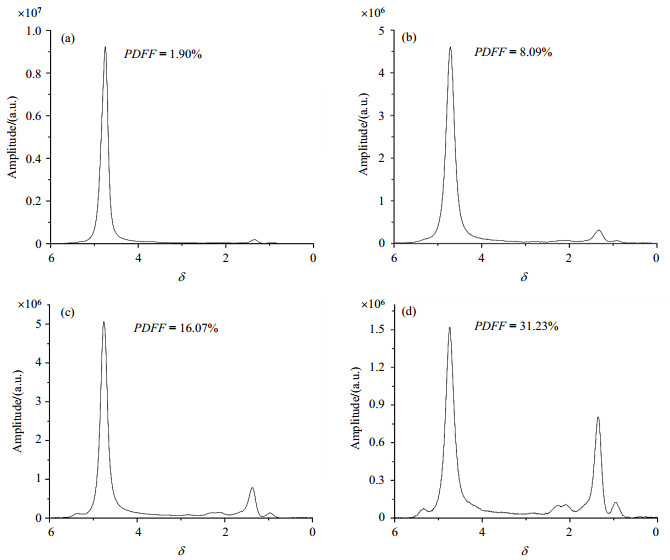
|
图 6 不同脂肪浓度的人体肝脏在TE=12 ms的磁共振波谱. (a)正常;(b)轻度脂肪沉积;(c)中度脂肪沉积;(d)重度脂肪沉积 Figure 6 MR spectra of the human livers with various fat concentrations at TE=12 ms. (a) Normal; (b) Mild steatosis; (c) Moderate steatosis; (d) Severe steatosis |
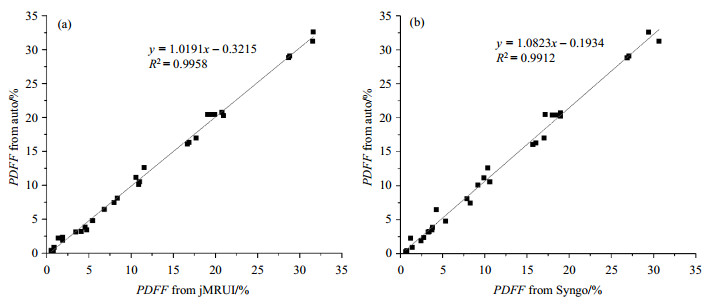
|
图 7 人体肝脏PDFF测量结果对比. (a)自动后处理算法(auto)与jMRUI软件得到的PDFF线性回归分析;(b)自动后处理算法与西门子Syngo软件得到的PDFF线性回归分析 Figure 7 Comparison of measured PDFF values in the human livers. (a) Linear regression analysis between the automated post-processing algorithm and jMRUI software; (b) Linear regression analysis between the automated post-processing algorithm and Siemens Syngo software |
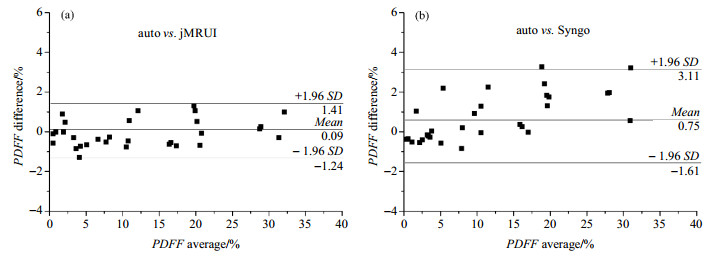
|
图 8 人体肝脏不同后处理方法得到PDFF的结果Bland-Altman分析 Figure 8 Bland-Altman analysis comparing PDFF measurements in the human livers with various post-processing methods |
| 表 3 人体肝脏自动后处理算法、jMRUI软件和西门子Syngo软件处理得到的脂肪质子和水质子的T2值 Table 3 T2 values of water and fat in human livers obtained from automated post-processing algorithm, jMRUI software and Siemens Syngo software |
针对目前肝脏脂肪含量的定量计算方法不足,本文提出了一种定量肝脏脂肪的自动后处理算法.通过水脂模型和人体肝脏对比研究发现,自动后处理算法得到的结果和jMRUI得到的结果高度一致,但自动定量算法比jMRUI处理迅速和客观.同时,本文也将自动后处理算法得到的结果与西门子Syngo软件处理结果进行对比,后者较前者低估了脂肪含量.从理论上讲,脂肪应含有九个可见脂肪质子峰,化学位移分别为δ 0.90、1.30、1.60、2.02、2.24、2.75、4.20、5.19和5.29.西门子Syngo软件提供的后处理算法以δ 3.60为分界点,化学位移小于δ 3.60的谱峰为脂肪信号,大于δ 3.60的谱峰为水信号,这样δ 4.20、5.19以及5.29处脂肪峰就被错当作水峰,因此求得的脂肪含量比实际结果要小,这在本文水脂模型和人体肝脏测量中均得到了验证.
由于脂肪质子和水质子信号均会随着回波时间按不同的T2指数衰减,因此进行T2衰减校正是脂肪定量必不可少的步骤,而且T2拟合的准确性会影响脂肪定量的准确性.本文在拟合脂肪质子T2时,认为所有脂肪峰的T2是相同的,而实际上脂肪各个谱峰的T2略有差别[19, 26].肝脏T2配对t检验结果显示,Syngo软件得到的肝脏脂肪质子T2显著低于本文提出的自动后处理算法和jMRUI软件,而Syngo软件得到的肝脏水峰质子T2显著高于自动后处理算法和jMRUI软件的结果,其可能原因是:Syngo软件将大于δ 3.60的谱峰均当成水信号,这样其计算所用脂肪峰仅包含小于δ 3.60的脂肪峰,计算水峰T2还包含大于δ 3.60的脂肪峰的贡献.对于水模的脂肪质子和水质子的T2,自动后处理算法得到的结果与jMRUI软件没有显著性差异,自动后处理算法与Syngo软件得到的结果也没有显著性差异,其可能原因是:Syngo软件选择δ 3.60作为水峰和脂肪峰分割点,而在场不均匀的情况下,水模中TWEEN-80的信号峰会在δ 3.60左右偏移,因此该峰有可能被划归为水质子,也有可能被划归为脂肪质子;TWEEN-80的信号峰被划分的不确定性导致Syngo所得到的T2值误差很大,从而得到了方差较大的配对t检验结果,所以Syngo所得到的T2值是不可信的.
jMRUI软件内置仅有高斯和洛仑兹两种线型,所以本文在使用jMRUI软件处理波谱数据时采用了这两种线型.而本文自动后处理算法选用的拟合线型既非高斯也非洛仑兹,这是因为主磁场的不均匀性会导致VOI内质子共振频率展宽,所采集到的谱峰实际上既不是完美的高斯线型也不是完美的洛仑兹线型,而是它们两者的结合,即高斯线型展宽的洛仑兹线型,在数学上可以用佛克脱线型表示[18],然后采用一个水峰和限定了幅值比、半高宽、化学位移的九个脂肪峰分别拟合水质子和脂肪质子的信号,可得到更为精确的PDFF.
从理论上,水脂模型的脂肪含量参考值可以同步利用已知的脂肪含量,但是水脂模型在制备过程加入了表面活性剂和琼脂等化学物质,另外由于人为或仪器等各方面因素会产生不可避免的误差,因此脂肪含量无法精确计算出.jMRUI软件定量MRS脂肪含量的准确性已经被广泛认可,是目前MRS后处理的金标准[27, 28],所以本研究选用jMRUI软件的结果作为参考值.
本研究提出的定量肝脏脂肪自动后处理算法有以下不足:(1)在目前的算法中,仍需要一些人为设定的参数,这些参数的设定主要基于目前的相关文献;(2)因为拟合采用一个水峰和九个脂肪峰,如果扫描之前匀场不好导致出现双峰现象,那么在寻找水峰和最高脂肪峰会出现偏差,可能会导致拟合错误.
4 结论采用jMRUI软件定量肝脏脂肪是目前肝脏定量的金标准,但是其处理步骤繁琐,且人为控制因素太多.本文将肝脏脂肪定量步骤自动化,并采用和实际谱线更为接近的佛克脱线型对原始MRS谱线进行拟合,很大程度提高了处理效率,而且也更具有普适性.
| [1] | SANYAL A J, BANAS C, SARGEANT C, et al. Similarities and differences in outcomes of cirrhosis due to nonalcoholic steatohepatitis and hepatitis C[J]. Hepatology, 2006, 43(4): 682-689. DOI: 10.1002/(ISSN)1527-3350. |
| [2] | EKSTEDT M, FRANZéN L E, MATHIESEN U L, et al. Long-term follow-up of patients with NAFLD and elevated liver enzymes[J]. Hepatology, 2006, 44(4): 865-873. DOI: 10.1002/(ISSN)1527-3350. |
| [3] | KINNER S, REEDER S B, YOKOO T. Quantitative imaging biomarkers of NAFLD[J]. Dig Dis Sci, 2016, 61(5): 1337-1347. DOI: 10.1007/s10620-016-4037-1. |
| [4] | RAJARSHI B, MICHAEL P, TUNNICLIFFE E M, et al. Multiparametric magnetic resonance for the non-invasive diagnosis of liver disease[J]. J Hepatol, 2014, 60(1): 69-77. DOI: 10.1016/j.jhep.2013.09.002. |
| [5] | HERNANDO D, HALDAR J P, SUTTON B P, et al. Joint estimation of water/fat images and field inhomogeneity map[J]. Magn Reson Med, 2008, 59(3): 571-580. DOI: 10.1002/(ISSN)1522-2594. |
| [6] | MA X, HOLALKERE N S, KAMBADAKONE R A, et al. Imaging-based quantification of hepatic fat:methods and clinical applications[J]. Radiographics, 2009, 29(5): 1253-1277. DOI: 10.1148/rg.295085186. |
| [7] |
WANG L L, ZHU Y, ZHONG K. Progresses in MRI and MRS studies on obesity[J].
Chinese J Magn Reson, 2016, 33(1): 168-178.
王璐璐, 朱勇, 钟凯. MRI与MRS在肥胖症研究中的应用进展[J]. 波谱学杂志, 2016, 33(1): 168-178. |
| [8] | HORNG D E, HERNANDO D, REEDER S B. Quantification of liver fat in the presence of iron overload[J]. J Magn Reson Imaging, 2017, 45(2): 428-439. DOI: 10.1002/jmri.v45.2. |
| [9] | TOWBIN A J, SERAI S D, PODBERESKY D J. Magnetic resonance imaging of the pediatric liver:imaging of steatosis, iron deposition, and fibrosis[J]. Magn Reson Imaging Clin N Am, 2013, 21(4): 669-680. DOI: 10.1016/j.mric.2013.05.001. |
| [10] | HAMILTON G, MIDDLETON M S, BYDDER M, et al. The effect of PRESS and STEAM sequences on magnetic resonance spectroscopic liver fat quantification[J]. J Magn Reson Imaging, 2009, 30(1): 145-152. |
| [11] | REEDER S B, CRUITE I, HAMILTON G, et al. Quantitative assessment of liver fat with magnetic resonance imaging and spectroscopy[J]. J Magn Reson Imaging, 2011, 34(4): 729-749. DOI: 10.1002/jmri.v34.4. |
| [12] | MEISAMY S, HINES C D, HAMILTON G, et al. Quantification of hepatic steatosis with T1-independent, T2-corrected MR imaging with spectral modeling of fat:blinded comparison with MR spectroscopy[J]. Radiology, 2011, 258(3): 767-775. DOI: 10.1148/radiol.10100708. |
| [13] | HAMILTON G, MIDDLETON M S, HOOKER J C, et al. In vivo breath-hold 1H MRS simultaneous estimation of liver proton density fat fraction, and T1 and T2 of water and fat, with a multi-TR, multi-TE sequence[J]. J Magn Reson Imaging, 2015, 42(6): 1538-1543. DOI: 10.1002/jmri.24946. |
| [14] | PINEDA N, SHARMA P, XU Q, et al. Measurement of hepatic lipid:high-speed T2-corrected multiecho acquisition at 1H MR spectroscopy--a rapid and accurate technique[J]. Radiology, 2009, 252(2): 568-576. DOI: 10.1148/radiol.2523082084. |
| [15] | KRSSAK M, HOFER H, WRBA F, et al. Non-invasive assessment of hepatic fat accumulation in chronic hepatitis C by 1H magnetic resonance spectroscopy[J]. Eur J Radiol, 2010, 74(3): 60-66. DOI: 10.1016/j.ejrad.2009.03.062. |
| [16] |
LI J Q, WU B, TANG F, et al. In vivo 1H MRS of liver:The effects of frequency correction[J].
Chinese J Magn Reson, 2007, 24(3): 335-340.
李建奇, 吴斌, 唐峰, 等. 频率校正方法在活体肝脏1H磁共振波谱中的应用[J]. 波谱学杂志, 2007, 24(3): 335-340. DOI: 10.3969/j.issn.1000-4556.2007.03.013. |
| [17] | MARSHALL I, HIGINBOTHAM J, BRUCE S, et al. Use of voigt lineshape for quantification of in vivo 1H spectra[J]. Magnc Reson Med, 1997, 37(5): 651-657. DOI: 10.1002/(ISSN)1522-2594. |
| [18] | KRIESTEN E, MAYER D, ALSMEYER F, et al. Identification of unknown pure component spectra by indirect hard modeling[J]. Chemometr Intell Lab, 2008, 93(2): 108-119. DOI: 10.1016/j.chemolab.2008.05.002. |
| [19] | HAMILTON G, YOKOO T, BYDDER M, et al. In vivo characterization of the liver fat 1H MR spectrum[J]. NMR Biomed, 2011, 24(7): 784-790. DOI: 10.1002/nbm.v24.7. |
| [20] | CHEN L, WENG Z Q, GOH L Y, et al. An efficient algorithm for automatic phase correction of NMR spectra based on entropy minimization[J]. J Magn Reson Imaging, 2002, 158(1): 164-168. |
| [21] | BAO Q J, FENG J W, CHEN L, et al. A robust automatic phase correction method for signal dense spectra[J]. J Magn Reson Imaging, 2013, 234(8): 82-89. |
| [22] |
HU B H, YUAN H Z, GUO J X, et al. Determination of plant oils by 1H and 13C NMR[J].
Chinese J Magn Reson, 1993, 10(3): 251-259.
胡邦豪, 袁汉珍, 郭建新, 等. 植物油的1H NMR和13C NMR的测定[J]. 波谱学杂志, 1993, 10(3): 251-259. |
| [23] | BERNARD C P, LINEY G P, MANTON D J, et al. Comparison of fat quantification methods:a phantom study at 3.0 T[J]. J Magn Reson Imaging, 2008, 27(1): 192-197. |
| [24] | CATHERINE M, YU H, MSE A, et al. T1 independent, T2* corrected MRI with accurate spectral modeling for quantification of fat:Validation in a fat-water-SPIO phantom[J]. J Magn Reson Imaging, 2009, 30(5): 1215-1222. DOI: 10.1002/jmri.v30:5. |
| [25] | VAN WERVEN J R, SCHREUDER T C, NEDERVEEN A J, et al. Hepatic unsaturated fatty acids in patients with non-alcoholic fatty liver disease assessed by 3.0 T MR spectroscopy[J]. Eur J Radiol, 2010, 75(2): 102-107. DOI: 10.1016/j.ejrad.2009.12.033. |
| [26] | REN J M, IVAN D, DEAN S A, et al. Composition of adipose tissue and marrow fat in humans by 1H NMR at 7 Tesla[J]. J Lipid Res, 2008, 49(9): 2055-2062. DOI: 10.1194/jlr.D800010-JLR200. |
| [27] | KANG G H, CRUITE I, SHIEHMORTEZA M, et al. Reproducibility of MRI-determined proton density fat fraction across two different MR scanner platforms[J]. J Magn Reson Imaging, 2011, 34(4): 928-934. DOI: 10.1002/jmri.v34.4. |
| [28] | VU K N, GILBERT G, CHALUT M, et al. MRI-determined liver proton density fat fraction, with MRS validation:Comparison of regions of interest sampling methods in patients with type 2 diabetes[J]. J Magn Reson Imaging, 2015, 43(5): 1090-1099. |
 2018, Vol. 35
2018, Vol. 35 
