2. Department of Radiology, Weill Medical College of Cornell University, Ithaca, New York, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York, USA
2. Department of Radiology, Weill Medical College of Cornell University, Ithaca, New York, USA;
3. Department of Biomedical Engineering, Cornell University, Ithaca, New York, USA
磁共振成像(magnetic resonance imaging,MRI)的质子密度脂肪分数(proton density fat fraction,PDFF)是用于评估肝脏脂肪的重要定量生物标志物[1],它定义为组织内甘油三酯的质子密度与甘油三酯和水中总质子密度的比值[2-4].在消除所有的相关影响因素时,组织的PDFF就相当于其脂肪分数.由于PDFF能够准确反映肝脏脂肪性病变的存在及其程度,因此被用作临床上对非酒精性脂肪肝等疾病检测的诊断和分期[5-7].
MRI水脂分离技术主要有基于复值重建和基于模值重建两类方法.基于回波不对称和最小二乘的水脂迭代分解(iterative decomposition of water and fat with echo asymmetry and least-squares, IDEAL)方法[8]是现阶段比较主流且成熟的复值重建水脂分离方法,其源于Dixon原理,回波时间可灵活变化,而且在分离出水和脂肪信号的同时,可得到较为准确的B0场不均匀性图像.由其发展而来的T2*-IDEAL算法[9]可以去除磁共振信号随R2*(组织T2*的倒数)衰减所带来的误差,估计出更为准确的脂肪分量和B0场.但是IDEAL算法对于源图的相位误差非常敏感,尤其脂肪含量较低时,相位误差会导致PDFF误差较大[10, 11].而基于模值的重建方法一般使用Levenberg-Marquardt(LM)最小二乘迭代方法,其相对复值重建方法而言,对于相位误差不敏感,然而在PDFF接近50%的区域内的噪声性能较差.
鉴于复值重建和模值重建算法不同的水脂定量特点,Yu等人[10]提出了一种基于复值图像和模值图像加权组合的混合方法,可得到更为准确的PDFF图像,并通过1.5 T MRI扫描验证了其算法的可行性.其混合方法中所选取的模值重建算法使用了矫正R2*衰减后的模值数据,而用于模值数据矫正的R2*通过T2*-IDEAL算法计算得到.然而有研究表明[11],T2*-IDEAL算法低估了肝脏的实际R2*值,可能会导致模值重建结果存在误差,从而影响最终的水脂分离结果的准确性.本文从改进混合水脂分离方法出发,通过综合各种水脂分离方法的优劣以及R2*的分离矫正,得到了更为准确的PDFF图像,并在3.0 T MRI扫描仪上对肝脏脂肪含量不同的人体被试进行MRI扫描,验证本文方法的准确性.
1 材料与方法 1.1 算法 1.1.1 基于复值重建的水脂分离算法对于MRI梯度回波序列在离散的回波时间tn(n = 1, 2, …, N, N为回波数)采集得到的图像,如果使用小翻转角则可忽略T1影响,那么水和脂肪模型的总体信号Sn可以采用(1)式描述[8]:
| $ {S_n} = ({M_{\rm{w}}} + {M_{\rm{f}}}\sum\limits_{p = 1}^P {{\alpha _p}{{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}\Delta {f_p}{t_n}}}){{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}\psi {t_n}}}} $ | (1) |
其中,Mw和Mf分别是水和脂肪的幅度值;相对模值
| 表 1 脂肪九峰模型中每个谱峰的化学位移及其对总脂肪信号的相对贡献[13] Table 1 The chemical shift (δ) and relative contribution to the total fat signal of each fat peak in 9-peak fat model[13] |
考虑到R2*衰减所带来的影响后,水脂信号模型Sn修正为[9]:
| $ {S_n} = ({M_{\rm{w}}} + {M_{\rm{f}}}\sum\limits_{p = 1}^P {{\alpha _p}{{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}\Delta {f_p}{t_n}}}){{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}\psi {t_n}}}{{\rm{e}}^{ - R_2^*{t_n}}}} $ | (2) |
其中,
显然,由于加入了R2*衰减项,(2)式对于水脂信号的模拟更加准确.(1)式和(2)式都可以通过复值最小二乘法解得水脂定量结果,但由于其迭代速度过慢,一般使用IDEAL算法和T2*-IDEAL算法来对两者进行水脂分离求解.相比IDEAL算法,T2*-IDEAL算法消除了R2*衰减的影响,理论上可以得到更加精准的水脂比例.然而,无论是IDEAL还是T2*-IDEAL算法,所得到的水脂分离结果仍然存在一系列的问题.
首先,IDEAL算法对相位误差都特别敏感,尤其是在高、低脂肪分数区域[10].由于相位误差的存在,在低脂肪分数区域,IDEAL算法所测得的PDFF绝对偏差可以达到约5%.例如,真正的PDFF为0.9%,但通过IDEAL算法得到的结果却为5.9%,而5.56%以上的PDFF通常被认为是不正常的[7, 14-16].因此,采集信号的相位误差可能会导致临床上非酒精性脂肪肝的错误诊断.
其次,由T2*-IDEAL算法所得到的R2*估计值也相对R2*的真实值偏小[11],这将在后文提及.
1.1.2 基于模值重建的水脂分离算法对(2)式两端取模,可以得到如下信号关系:
| $ |{S_n}| = \left| {({M_{\rm{w}}} + {M_{\rm{f}}}\sum\limits_{p = 1}^P {{\alpha _p}{{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}\Delta {f_p}{t_n}}}){{\rm{e}}^{ - R_2^*{t_n}}}} } \right| $ | (3) |
可以看到,通过取模运算,可消除主磁场B0不均匀性所带来的影响,也就是说,基于模值重建的方法对相位误差不敏感[10].模值重建使用带信赖域的LM最小二乘方法进行拟合,通过限定水、脂肪以及R2*信号的信赖区间,不仅可以改善T2*-IDEAL算法的错误估计,而且确保了最终拟合结果的收敛性.此外,相比T2*-IDEAL算法,基于模值重建的LM最小二乘方法得到的R2*估计值更接近真实R2*值[11].
但是,基于模值的最小二乘法无法使用相位信息来唯一标定水和脂肪的信号,因此仅仅通过模值重建无法获得水和脂肪图像.我们必须使用复值重建算法得到的结果作为模值重建的初始猜测值[10].相比于复值重建算法,模值重建不存在相位误差,可以被看作是从复数重建微调的解决方案,以提供更准确的脂肪成分估计.
1.1.3 基于复值和模值图像加权组合的混合方法[10]由于相位误差的存在,复值重建的水脂结果在高、低脂肪区域容易导致水脂比例的错误估计[11];而模值重建需要先验的水脂估计值,其在水脂比例差别比较大的区域可以较快收敛到准确值,但在水脂比例差别不大的情况下,基于模值的重建常常信噪比较差,所以使用复值和模值重建结果加权的形式可得到综合两者优点的更为精确的PDFF图像[10]:
| $ \left\{ \begin{array}{l} W = \lambda \cdot {W_{\rm{c}}} + (1 - \lambda ) \cdot {W_{\rm{m}}}\\ F = \lambda \cdot {F_{\rm{c}}} + (1 - \lambda ) \cdot {F_{\rm{m}}} \end{array} \right. $ | (4) |
这里,Wc和Fc分别为复值重建的水、脂比例结果,Wm和Fm分别为模值重建的水、脂比例结果,而W和F分别为最终组合重建的水、脂比例结果.(4)式中λ为费米函数,用于确定最终图像中复值和模值水脂重建结果所占比率[17],当脂肪分数接近于0%或者100%时,λ接近于0;当脂肪分数接近于50%时,λ接近于1.
在混合方法中,用于加权的复值重建结果由一开始的T2*-IDEAL算法得到.在得到初始的R2*估计后,将原始复值信号除以T2*-IDEAL算法所提供的R2*衰减因子,然后将此信号与T2*-IDEAL算法得到的初始水脂比放入模值重建方法中进行迭代,得到最终用于加权的模值重建结果.将以上两种方法所得到的结果按照(4)式进行加权组合,从而得到最终的PDFF图像.
然而这种混合方法也存在一些问题:该算法采用T2*-IDEAL算法重建得到的R2*来矫正用于模值重建的多回波数据,而复值数据中相位误差会导致T2*-IDEAL算法在高、低脂肪分数区域容易得到错误的水脂定量结果[10],水脂定量的错误会导致R2*结果的不可靠性.另外仿真结果表明[11],T2*-IDEAL算法所得到的R2*值相对真实值偏小.R2*的不准确可能会造成混合方法中的模值拟合算法得到的水脂比例的偏差,从而使得最终得到的组合结果产生偏差.
1.1.4 本文提出的基于分离R2*估计的改进混合方法为了克服上述混合算法的问题,我们提出了一种基于分离R2*估计的改进混合方法.该方法使用IDEAL算法得到初始的粗略水脂定量结果,然后将此粗略水脂定量结果作为初始值传入LM模值拟合算法进行迭代,得到基于模值重建的精确水脂定量结果和R2*值.尽管IDEAL拟合得到的初值并不精确,但该初值已接近全局最优,LM算法就可以迅速收敛到全局最优解.接下来,将原始复值信号除以
本文所提出的基于分离R2*估计的改进混合方法如图 1所示,其具体步骤如下:
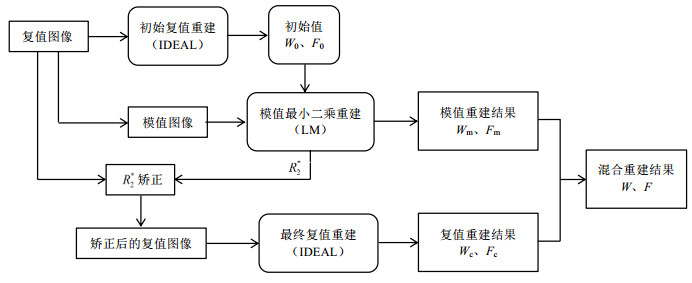
|
图 1 基于分离R2*估计的混合方法流程 Figure 1 The flow chart of mix method based on separate R2* estimation |
(1)将MRI采集到的多回波模值图像和相位图像数据变换为多回波复值图像数据,并将原始的多回波模值图像保存,以便模值拟合使用.
(2)将多回波复值图像数据导入IDEAL算法,求解出水和脂肪的初始比例,用于模值拟合的水、脂比例初始值.
(3)将多回波模值图像数据导入LM模值拟合算法,将初始水、脂比例作为LM模值拟合算法的初始值,得到模值重建后的水、脂比例估计以及R2*图像.
(4)将多回波复值图像数据除以R2*衰减系数,并导入IDEAL算法中,得到复值重建后的水、脂比例估计.
(5)将第(3)步和第(4)步所得结果按照(4)式所描述的方式加权,得到最终混合加权的PDFF图像.
1.2 人体MRI数据采集实验招募12名被试[10名男性、2名女性,年龄为(31.4±9.0)岁,体重为(84.6±16.6)kg]参与本研究.在正式实验之前,要求被试认真阅读《知情同意书》并签字,本研究通过了华东师范大学人体伦理委员会批准.
MRI数据采集使用3 T MRI扫描仪(Siemens MAGNETOM Prisma 3 T),数据接收采用8通道体部线圈.扫描序列为多回波Dixon序列,序列参数为:重复时间(TR)=12 ms,第一回波时间(TE1)=1.11 ms,回波间隔(ΔTE)=1.86 ms,回波数=6,体素大小=1.56 mm×1.56 mm×4 mm,视野(FOV)=300 mm×400 mm,层数=32,翻转角(FA)=5°.该序列总扫描时间共20 s,均在被试屏气时完成.
为了对本文所提出的水脂分离方法应用于人体肝脏脂肪定量的准确性进行评估,我们使用磁共振波谱(magnetic resonance spectroscopy, MRS)处理结果作为对比[7, 18],对每个被试同时使用快速T2校正多回波波谱采集序列(high-speed T2 corrected multi-echo acquisition,HISTO)进行MRS采集,采集参数如下:TR= 3 000 ms,混合时间(TM)= 10 ms, TE= 12、24、36、48和72 ms,平均次数=1, 带宽=1 200 Hz,采样点数=1 024,体素大小=30 mm×30 mm×30 mm.利用T1加权定位像将波谱感兴趣体素(voxel of interest, VOI)定位在肝脏右叶的合适位置,定位时避开皮下脂肪以及血管结构.序列总扫描时间共15 s,均被试屏气时完成.
1.3 数据处理及分析所有复值重建算法均在Matlab平台(Matlab R2014b,MathWorks)实现,模值重建算法在Visual Studio 2013平台上编译成dll,并使用上述的Matlab平台调用.算法运行环境为:64位Windows 8.1专业版操作系统,CPU型号为i7-6700HQ,系统内存大小为8 GB.将12名被试肝脏磁共振数据分别使用T2*-IDEAL算法、LM算法、Yu提出的混合方法以及本文改进的混合方法处理,分别得到水脂分离结果,并计算得到PDFF.在以上的水脂分离算法中,脂肪模型均选取表 1所示的九峰脂肪模型.为了保证复值拟合时全局最优解并加快迭代速度,采用图割算法[19]得到场图作为初始值传给T2*-IDEAL以及本文改进的混合方法(1.1.4节)中的第(1)步IDEAL算法.
为了对比Yu提出的混合方法和本文的混合方法的重建时间,我们还对这两种方法中主要步骤的迭代时间进行了统计分析.在本文的混合方法中,由于第一次的IDEAL算法仅用于初始值估计,无需精确迭代,所以其采用了较少的迭代次数(2次),而最终的IDEAL复值重建算法的迭代次数为5次,LM算法的迭代次数为10次.Yu提出的混合方法中T2*-IDEAL重建拟合和LM模值重建算法中的迭代次数与我们混合方法保持一致.
利用jMRUI软件分析处理HISTO波谱数据,处理步骤如下:首先将水峰的化学位移设置到δ 4.70处,同样采用九脂肪峰的模型拟合,拟合线型使用洛仑兹线型,通过固定各峰幅值比、限定各峰半高宽范围等操作,拟合得到各峰的面积;将各个TE时刻的水、脂肪面积分别进行T2拟合,得到水和脂肪的幅度值,最终通过计算得到VOI中的实际脂肪含量.
读取波谱数据的VOI定位信息,计算得到磁共振图像上VOI对应区域内所有像素PDFF的平均值,并将该PDFF平均值与MRS处理结果进行相关性分析.
2 结果与讨论 2.1 结果表 2总结了在同样的运行环境以及相同的最大迭代次数下Yu提出的混合方法以及本文改进的混合方法主要算法运行所需要的平均时间.Yu提出的混合方法中,T2*-IDEAL算法平均计算时间为14.2 s,去除R2*衰减后LM算法平均计算时间为168.7 s,这两个步骤总平均时间为182.9 s;而本文改进的混合算法中,初始IDEAL算法的平均计算时间为21.2 s,矫正R2*衰减后LM算法的平均计算时间为80.4 s,最终IDEAL算法的平均计算时间为45.0 s,这三个步骤总平均时间为146.6 s.
| 表 2 两种混合方法的主要算法运行所需要的平均时间统计 Table 2 Mean durations of the main step in two mix methods |
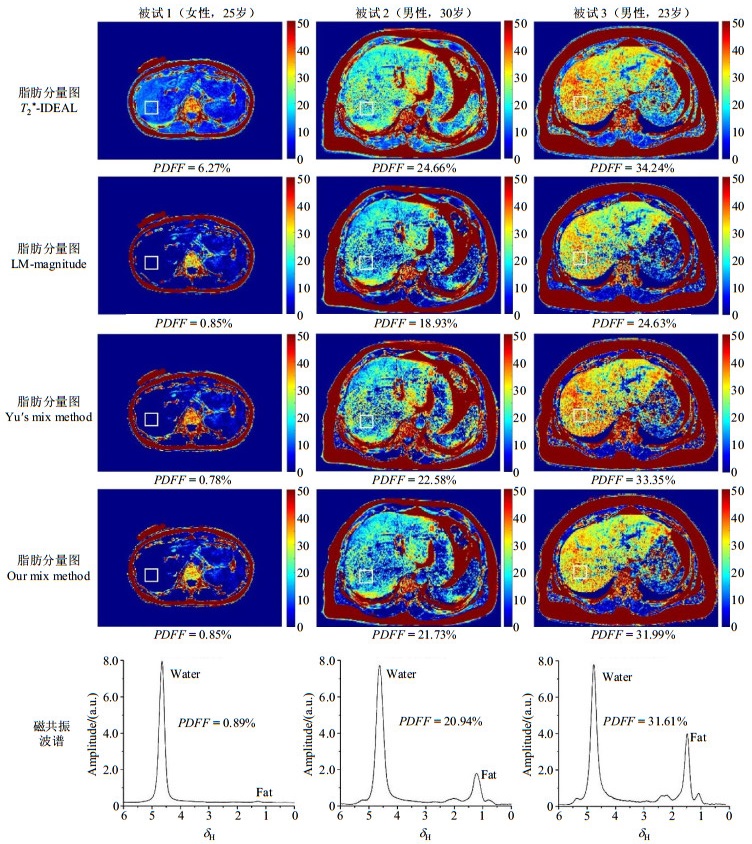
图 2显示了肝脏脂肪分数较低、中等以及较高的三名典型被试分别采用T2*-IDEAL算法、LM算法、Yu提出的混合方法以及本文改进的混合方法得到的肝脏PDFF图像和相应的MRS.对于第1名肝脏脂肪分数较低的被试,MRS得到的PDFF为0.89%,使用T2*-IDEAL算法、LM算法、Yu提出的混合方法以及本文改进的混合方法计算结果分别为6.27%、0.85%、0.78%和0.85%,T2*-IDEAL算法得到的PDFF明显偏高;对于第2名肝脏脂肪分数中等的被试,MRS得到的PDFF为20.94%,使用T2*-IDEAL算法、LM算法、Yu提出的混合方法以及本文改进的混合方法计算结果分别为24.66%、18.93%、22.58%和21.73%,本文改进的混合方法得到的结果与MRS得到的结果最为接近;对于第3名肝脏脂肪分数较高的被试,MRS得到的PDFF为31.61%,而使用T2*-IDEAL算法、LM算法、Yu提出的混合方法以及本文改进的混合方法计算结果分别为34.24%、24.63%、33.35%和31.99%,LM算法得到的结果明显偏低,本文改进的混合方法得到的结果与MRS得到的结果最为接近.
|
图 2 三名肝脏脂肪含量不同的被试采用4种水脂分离方法处理得到的脂肪分量图以及对应的磁共振波谱.PDFF值为感兴趣体素对应区域内(白色方框)的所有像素PDFF的平均值 Figure 2 Liver PDFF maps and magnetic resonance spectra of three subjects with different liver fat fractions obtained from T2*-IDEAL, LM magnitude method, Yu's mix method and our improved mix method. The PDFFis the mean value from all pixels in the VOI (white square) |
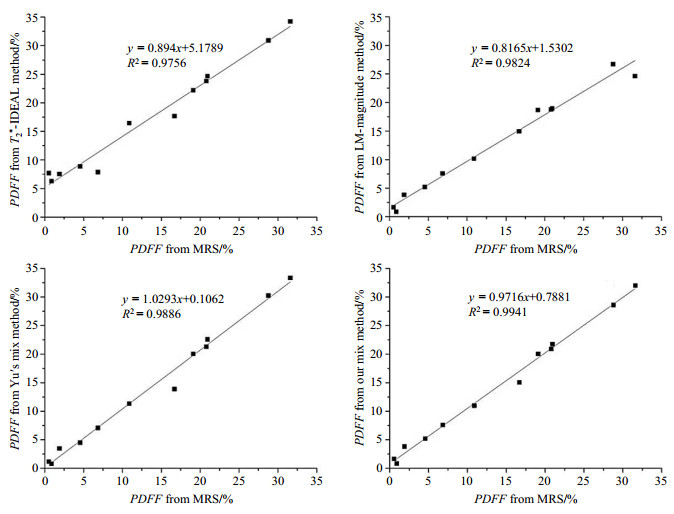
图 3依次为T2*-IDEAL算法、模值LM算法、Yu提出的混合方法、本文改进的混合方法与MRS的相关性分析结果.相对于MRS,T2*-IDEAL算法在PDFF < 20%的低脂肪分数区域,脂肪分数的估计偏高,但在20%~35%的区域表现较为平稳.相对于MRS,LM算法在PDFF=30%左右的两个点都明显地低估了脂肪的贡献,这正是由于模值拟合在此区域内信噪比较差的原因[11].从相关性分析图像上来看,Yu的混合方法与本文所述方法差别不是很大,但本文所述方法仍略优于Yu的混合方法,这是由于其使用了低估的R2*衰减图像,理论上这两种方法的差异在高铁沉积的情况下会更加明显.
|
图 3 4种水脂分离算法得到的肝脏脂肪分量与磁共振波谱的结果线性回归分析 Figure 3 Linear regression analysis of liver proton density fat fraction (PDFF) between various fat-water separation algorithms and MRS |
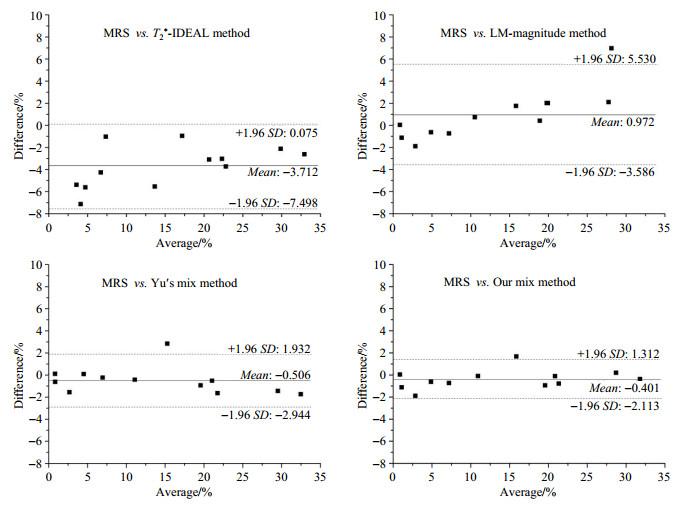
图 4依次为T2*-IDEAL算法、LM算法、Yu提出的混合方法、本文改进的混合方法与MRS结果进行线性回归分析得到PDFF的Bland-Altman分析图,可以看到:无论是对于单纯的T2*-IDEAL重建算法还是LM重建算法而言,其残差的均值普遍较大,T2*-IDEAL残差较大的区间在20%浓度以下,而LM算法残差较大的区间则集中在25%浓度以上.Yu提出的混合方法与本文所述方法的Bland-Altman结果差异不大,Yu提出的混合方法的残差均值为-0.506%,而本文方法的残差均值为-0.401%,都在临床可接受的范围之内,但本文方法残差均值较小.Yu的混合方法的95%的一致性界限区间为[-2.944%,1.932%],而本文方法的95%的一致性界限区间为[-2.113%,1.312%],这正是由于Yu的混合方法复值和模值重建都使用了低估的R2*估计,导致了其一致性界限范围的拓宽.
|
图 4 4种水脂分离算法得到的肝脏脂肪分量与磁共振波谱的Bland-Altman分析 Figure 4 Bland-Altman analysis of liver proton density fat fraction (PDFF) between various fat-water separation algorithms and MRS |
本文通过对复值重建和模值重建的利弊进行探讨以及对R2*衰减的评估,提出了一种可以更加精确定量肝脏内PDFF的方法.该方法结合模值重建和复值重建的优点,可以得到脂肪定量更准的水脂分离结果,并在人体不同程度肝脏脂肪实验中得到证实.
Yu所提出的混合方法是用T2*-IDEAL算法重建得到的R2*来矫正用于模值重建的多回波数据,但我们知道,使用模值重建的LM算法所得到的R2*是更为准确的[11],因此本文使用模值重建得到的R2*来矫正用于IDEAL算法重建的多回波数据.相比通过T2*-IDEAL算法直接重建出主磁场不均匀性和R2*图像,本文所提出的方法使用带信赖域限定的模值重建算法来计算R2*,得到了更为准确的R2*结果,不仅避免了可能由于R2*估计失误而导致一系列相关的水脂分离结果不可信,也增强了水脂分离算法的稳定性.
我们的方法增加了一个初始值估计的步骤,但比Yu提出的混合方法平均耗时更短,其可能原因是:Yu方法中第一步T2*-IDEAL算法低估了R2*,采用这个R2*矫正衰减后的模值数据偏离了真实数据点,在拟合中需要更多的时间求解全局最优.
我们看到,相比Yu的混合方法而言,本文方法的回归性分析结果并无较明显优势,这是由于本文所提及的基于R2*矫正的水脂分离方法理论上在较高铁沉积病人的优势更为明显,但由于我们所招募的被试都是正常人群,从而无法说明本文方法在较高铁沉积病人下的优势.我们将在今后的实验中进一步论证两种混合方法对铁沉积患者的差异性.
3 结论相比MRI中传统的脂肪抑制技术或MRS定量技术而言,水脂分离算法可以利用相位信息从原始信号中解调出水脂信号,就可以重建出高质量的PDFF图像,从而反映出整体肝脏内的脂肪含量分布状况.本文通过对现有水脂分离算法的优化重组,提出了一种新的基于分离R2*估计的肝脏脂肪精确定量方法,并得到了更为准确的PDFF图像,对肝脏脂肪性病变的诊断分期具有重要的参考意义.
| [1] | HAUFE W M, WOLFSON T, HOOKER C A, et al. Accuracy of PDFF estimation by magnitude-based and complex-based MRI in children with MR spectroscopy as a reference[J]. J Magn Reson Imaging, 2017, 46(6): 1641-1647. DOI: 10.1002/jmri.v46.6. |
| [2] | HERNANDO D, SHARMA S D, ALIYARI G M, et al. Multisite, multivendor validation of the accuracy and reproducibility of proton-density fat-fraction quantification at 1.5T and 3T using a fat-water phantom[J]. Magn Reson Med, 2017, 77(4): 1516-1524. DOI: 10.1002/mrm.v77.4. |
| [3] | KINNER S, REEDER S B, YOKOO T. Quantitative Imaging Biomarkers of NAFLD[J]. Dig Dis Sci, 2016, 61(5): 1337-1347. DOI: 10.1007/s10620-016-4037-1. |
| [4] | REEDER S B, HU H H, SIRLIN C B. Proton density fat-fraction:a standardized MR-based biomarker of tissue fat concentration[J]. J Magn Reson Imaging, 2012, 36(5): 1011-1014. DOI: 10.1002/jmri.v36.5. |
| [5] | LEPORQ B, LAMBERT S A, RONOT M, et al. Quantification of the triglyceride fatty acid composition with 3.0 T MRI[J]. NMR Biomed, 2014, 27(10): 1211-1221. DOI: 10.1002/nbm.3175. |
| [6] | WELLS S A. Quantification of hepatic fat and iron with magnetic resonance imaging[J]. Magn Reson Imaging Clin N Am, 2014, 22(3): 397-416. DOI: 10.1016/j.mric.2014.04.010. |
| [7] |
WANG L L, ZHU Y, ZHONG K. Progresses in MRI and MRS studies on obesity[J].
Chinese J Magn Reson, 2016, 33(1): 168-178.
王璐璐, 朱勇, 钟凯. MRI与MRS在肥胖症研究中的应用进展[J]. 波谱学杂志, 2016, 33(1): 168-178. |
| [8] | REEDER S B, WEN Z, YU H, et al. Multicoil Dixon chemical species separation with an iterative least-squares estimation method[J]. Magn Reson Med, 2004, 51(1): 35-45. DOI: 10.1002/(ISSN)1522-2594. |
| [9] | YU H Z, MCKENZIE C A, SHIMAKAWA A, et al. Multiecho reconstruction for simultaneous water-fat decomposition and T2* estimation[J]. J Magn Reson Imaging, 2007, 26(4): 1153-1161. DOI: 10.1002/(ISSN)1522-2586. |
| [10] | YU H Z, SHIMAKAWA A, HINES C D, et al. Combination of complex-based and magnitude-based multiecho water-fat separation for accurate quantification of fat-fraction[J]. Magn Reson Med, 2011, 66(1): 199-206. DOI: 10.1002/mrm.22840. |
| [11] | HERNANDO D, KRAMER J H, REEDER S B. Multipeak fat-corrected complex R2* relaxometry:theory, optimization, and clinical validation[J]. Magn Reson Med, 2013, 70(5): 1319-1331. DOI: 10.1002/mrm.v70.5. |
| [12] | REN J M, IVAN D, DEAN S A, et al. Composition of adipose tissue and marrow fat in humans by 1H NMR at 7 Tesla[J]. J Lipid Res, 2008, 49(9): 2055-2062. DOI: 10.1194/jlr.D800010-JLR200. |
| [13] | HAMILTON G, YOKOO T, BYDDER M, et al. In vivo characterization of the liver fat 1H MR spectrum[J]. NMR Biomed, 2011, 24(7): 784-790. DOI: 10.1002/nbm.v24.7. |
| [14] | MEISAMY S, HINES C D, HAMILTON G, et al. Quantification of hepatic steatosis with T1-independent, T2*-corrected MR imaging with spectral modeling of fat:blinded comparison with MR spectroscopy[J]. Radiology, 2011, 258(3): 767-775. DOI: 10.1148/radiol.10100708. |
| [15] | MACHANN J, THAMER C, SCHNOEDT B, et al. Standardized assessment of whole body adipose tissue topography by MRI[J]. J Magn Reson Imaging, 2005, 21(4): 455-462. DOI: 10.1002/(ISSN)1522-2586. |
| [16] | REEDER S B, SIRLIN C. Quantification of liver fat with magnetic resonance imaging[J]. Magn Reson Imaging Clin N Am, 2010, 18(3): 337-357. DOI: 10.1016/j.mric.2010.08.013. |
| [17] | HAACKE E M, BROWN R W, THOMPSON M R, et al. Magnetic resonance imaging:physical principles and sequence design[M]. New York: John Wiley & Sons, 1999. |
| [18] |
HU B H, YUAN H Z, GUO J X, et al. Determination of plant oils by 1H and 13C NMR[J].
Chinese J Magn Reson, 1993, 10(3): 251-259.
胡邦豪, 袁汉珍, 郭建新, 等. 植物油的1H NMR和13C NMR的测定[J]. 波谱学杂志, 1993, 10(3): 251-259. |
| [19] | DONG J W, LIU T, CHEN F, et al. Simultaneous phase unwrapping and removal of chemical shift (SPURS) using graph cuts:application in quantitative susceptibility mapping[J]. IEEE T Med Imaging, 2015, 34(2): 531-540. DOI: 10.1109/TMI.2014.2361764. |
 2018, Vol. 35
2018, Vol. 35 
